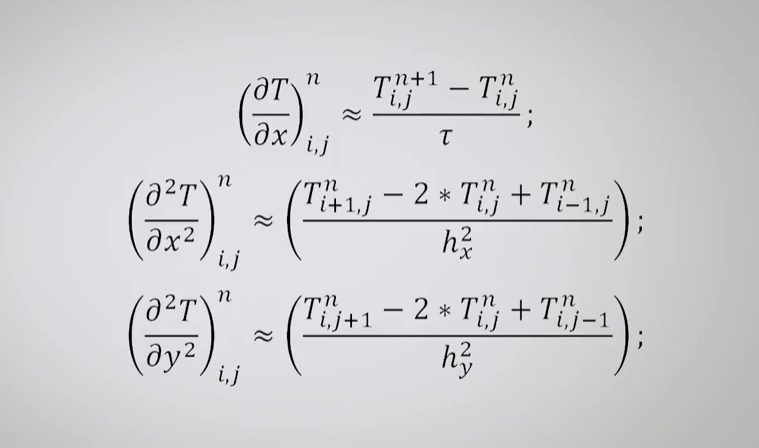Решение двумерного уравнения теплопроводности. Светличная Екатерина. 6 курс
Материал из Department of Theoretical and Applied Mechanics
Содержание
Цель[править]
Реализовать численное решение двумерного уравнения теплопроводности.
Постановка задачи[править]
Решается двумерное уравнение теплопроводности
С граничными условиями
И начальным распределением температуры
Конечно-разностная схема[править]
Задача содержит производную по времени первого порядка и производные по пространственным координатам второго порядка. Запишем конечно-разностные аналоги слагаемых, входящих в уравнение
Компьютерная реализация[править]
Компьютерную реализацию программы можно найти в Файл:Prill11.rar
Результаты[править]
| Количество процессов | Время рассчета (сек) |
|---|---|
| 1 | 5.77525 |
| 4 | 1.97889 |
| 9 | 91.8818 |
Выводы[править]
- При использовании более 4 процессов скорость расчета увеличивается из-за особенностей ПК.
- При увеличении числа процессоров скорость расчета уменьшается.