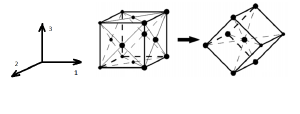
Разработка парного силового потенциала для описания структурного перехода ГЦК-ОЦК
Выпускная квалификационная работа
Выполнил: студент группы 43604/1 Н. Д. Мущак
Руководители: кандидат физ.-мат. наук Е. А. Подольская, ассистент А.Ю. Панченко
Содержание
Актуальность темы[править]
В настоящее время приобретают актуальность задачи, связанные с расчетами прочностных характеристик объектов, которые могут, в силу некоторых допущений, обладать бездефектной кристаллической структурой.Прочностные характеристики объектов тесно связаны с устойчивостью структуры материала. Внутренняя структура тел при потере устойчивости может претерпевать изменения.Изучение процессов потери устойчивости и структурных переходов очень важно в современной механике в силу необходимости оптимизации конструкций, так как многие инженерные задачи связаны с прочностными расчетами.
Цель работы[править]
Построение парного силового потенциала взаимодействия для описания устойчивости равновесия ГЦК и ОЦК структур.
Структурные фазовые переходы[править]
Процесс изменения внутренней упорядоченности частиц в кристалле может являться структурным переходом и зачастую связан с потерей устойчивости, потому что невозможно перейти из одной структуры в другую без перестроения кристаллической решетки.
Построение потенциала[править]
проводится в несколько этапов:
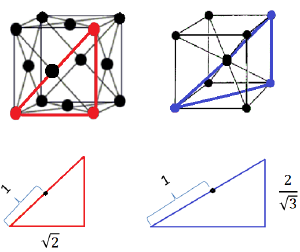
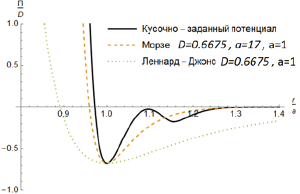
1)строятся две силы взаимодействия на базе потенциала Морзе, при этом пересечение графика силы с осью абсцисс положим равным 1-ым и 2-ым координационным сферам ГЦК и ОЦК (рис.2)
2)применяется сшивание двух кривых кубическим сплайном
3)используется укороченное взаимодействие для пренебрежения взаимодействием до 2-ой координационной сферы ГЦК
Анализ областей устойчивости[править]
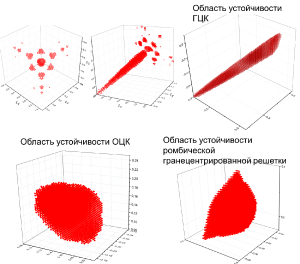
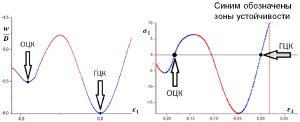
В ходе работы были получены области устойчивости в пространстве деформаций(рис.3). Было установлено, что зоны устойчивости соответствуют трем кристаллическим решеткам: гранецентрированная кубическая, объемноцентрированная кубическая и гранецентрированная ромбическая.
Также были построены профили для потенциальной энергии деформации и напряжения вдоль кривой одноосного сжатия.
Заключение[править]
В ходе выполнения данной работы были получены следующие результаты:
- построен парный силовой потенциал для математического моделирования структурного перехода ГЦК-ОЦК. Данный закон взаимодействия можно применять для описания структурных переходов, где фигурируют неплотноупакованные структуры, при этом надо учитывать геометрию решеток. Преимуществами данного потенциала являются универсальность, возможность описания широкого спектра материалов, в силу достаточного количества параметров, а также вычислительная простота.
- получены области устойчивости для ОЦК, ГЦК и ромбической гранецентрированной кристаллической решетки, а также проведен их анализ. Построены кривые для одноосного сжатия и потенциальной энергии деформации вдоль линии, соединяющей ненапряженную ГЦК с ненапряженной ОЦК, анализ которых показал, что профили кривых соответствуют структурному переходу ГЦК-ОЦК. Благодаря построенному закону взаимодействия получен ярко выраженный локальный минимум потенциальной энергии деформации для неплотноупакованной ОЦК решетки.
Список литературы[править]
[1] Metropolis N., Ulam S. The Monte Carlo method //Journal of the American statistical association. – 1949. – V. 44. – №. 247. – P. 335-341.
[2] Соболь И. М. Численные методы Монте-Карло – M.: Наука, 1973. – 313 с.
[3] Холмуродов Х. Т. и др. Методы молекулярной динамики для моделирования физических и биологических процессов //Физика элементарных частиц и атомного ядра. – 2003. – V. 34. – №. 2. – P. 474-515.
[4] Hoover W. G., Hoover C. G., Merritt E. C. Smooth-particle applied mechanics: Conservation of angular momentum with tensile stability and velocity averaging //Physical Review E. – 2004. – V. 69. – №. 1. – P. 16702.
[5] Cundall P. A., Strack O. D. L. A discrete numerical model for granular assemblies //Geotechnique. – 1979. – V. 29. – №. 1. – P. 47-65.
[6] Кривцов А. М., Кривцова Н. В. Метод частиц и его использование в механике деформируемого твердого тела //Дальневосточный математический журнал. – 2002. – V. 3. – №. 2. – P. 254-276.
[7] Подольская Е.А. Равновесие и устойчивость кристаллических твердых тел при малых и конечных деформациях: дис. … канд.физ.-мат. наук. Санкт-Петербургский Политехнический университет Петра Великого, Санкт-Петербург, 2013.
[8] Ercolessi F., Parrinello M., Tosatti E. Simulation of gold in the glue model //Philosophical magazine A. – 1988. – V. 58. – №. 1. – P. 213-226.
[9] Daw M. S., Baskes M. I. Semiempirical, quantum mechanical calculation of hydrogen embrittlement in metals // Physical Review Letters. – 1983. – V. 50. – №. 17. – P. 1285–1288
[10] Воропаев С.А., Днестровский А.Ю., Подольская Е.А., Душенко Н.В. N-алмаз: механика связей // Межвузовский сборник трудов. – 2014. – V.6. – №. 6. –P.74-81.
[11] Bain E. C., Dunkirk N. Y. The nature of martensite / E. C. Bain, N. Y. Dunkirk // Trans. Amer. Inst. Min. Metall. Eng. – 1924. – V. 70. – №. 1. – P. 25–46.
[12] Ашкрофт Н., Мермин Н. Физика твердого тела. – М.: Мир, 1979. – 77–85 c.
[13] Сиротин Ю. И., Шаскольская М. П. Основы кристаллофизики. — М.: Наука, 1979. — 640 - 715с.
[14] Теоретическая механика. Упругие и тепловые свойства идеальных кристаллов: учеб. пособие / И. Е. Беринский, Н. Г. Двас, А. М. Кривцов, А. М. Кударова, В. А. Кузькин, А. А. Ле- Захаров, О. С. Лобода, И. И Нейгебауэр, Е. А. Подольская; под ред. А.М. Кривцова. – СПб.: Изд-во Политехн. ун-та, 2009. – 144 с.
[15] Гуляев А.П. Металловедение. — М.: Металлургия,1986. — 229 – 231 c.
[16] Калетина Ю.В,. Герасимов Е.Г. Мартенситные превращения и магнитные свойства нестехиометрических сплавов системы Ni−Mn−In //Физика твердого тела, – 2014. – V. 56. – №.8 – P.1583-1587.
[17] Лободюк В. А., Эстрин Э. И. Мартенситные превращения – М.:Физматлит, 2009. –352 c.
[18] Бойко В. С., Гарбер Р. И. Г., Косевич А. М. Обратимая пластичность кристаллов – М.:Наука, 1991. – 431 c.
[19] Krivtsov A.M., Pavlovskaia E. E., Wiercigroch M. Impact fracture of rock materials due to percussive drilling action // CD-ROM Proceedings of 21st Internetional Congress of Theoretical and Applied Mechanics. – 2004. – Warsaw, Poland. – P. 275.
[20] Podolskaya E. A. et al. Loss of ellipticity and structural transformations in planar simple crystal lattices //Acta Mechanica. – 2016. – V. 227. – №. 1. – P. 185.
[21] Born M., Huang K., Lax M. Dynamical theory of crystal lattices //American Journal of Physics. – 1955. – V. 23. – №. 7. – P. 474-513.
[22] Milstein F., Fang H. E., Marschall J. Mechanics and energetics of the Bain transformation // Philosophical Magazine A. – 1994. – V. 70. – №. 4. – P. 621–639.