Определение эффективных механических характеристик материалов со случайной упаковкой частиц
Выпускная квалификационная работа
Выполнил: студент группы 43604/1 С.А. Воробьёв
Руководитель: кандидат физ.-мат. наук В.А. Кузькин
Введение[править]
Одна из основных проблем в использовании метода частиц для моделирования макроскопических процессов состоит в том, что регулярные упаковки частиц существенно анизотропны. Для достижения изотропии используются аморфные, нерегулярные упаковки частиц [1].
Модель и задачи[править]
Модель:
- Упаковка случайно размещенных частиц;
- Взаимодействие между частицами посредством линейных пружин;
Задачи:
- Создание модели;
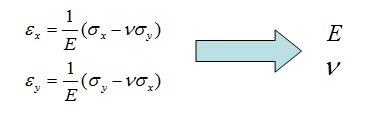
- Вычисление модуля Юнга, коэффициента Пуассона;
- Вычисление деформации разрушения;
Создание упаковки[править]
Создание модели аморфного материала происходит «набрасыванием» частиц; Для генерации частиц упаковка разделена на 9 ячеек; Место для появления новой частицы выбирается проверкой по расстоянию до соседних частиц в ячейке и до частиц в соседних ячейках;
Алгоритм[править]
Создается модель со случайной упаковкой частиц На образец материала накладывается мгновенная деформация в направлении одной из осей x или y Производится расчет напряжений
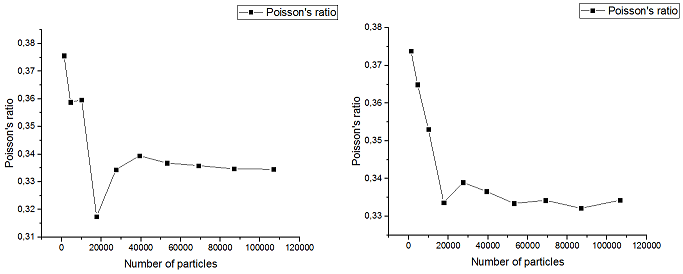
Результаты[править]
Выводы[править]
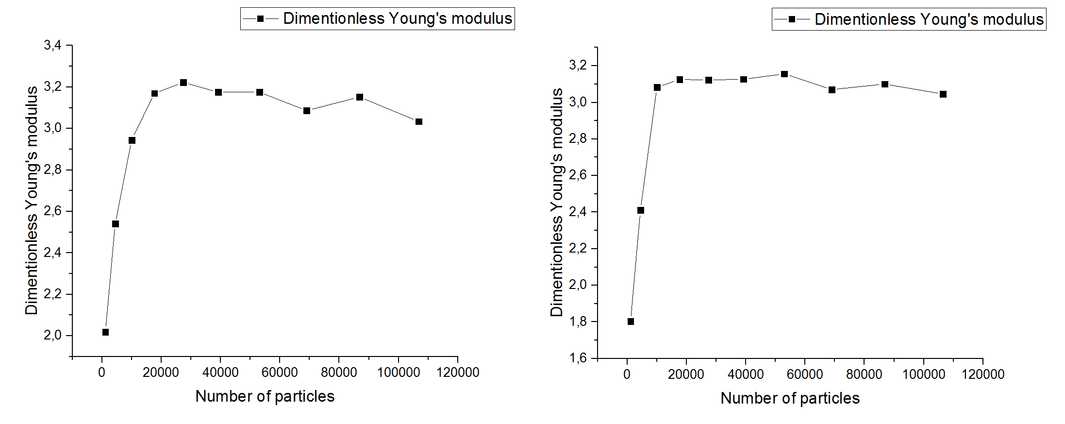
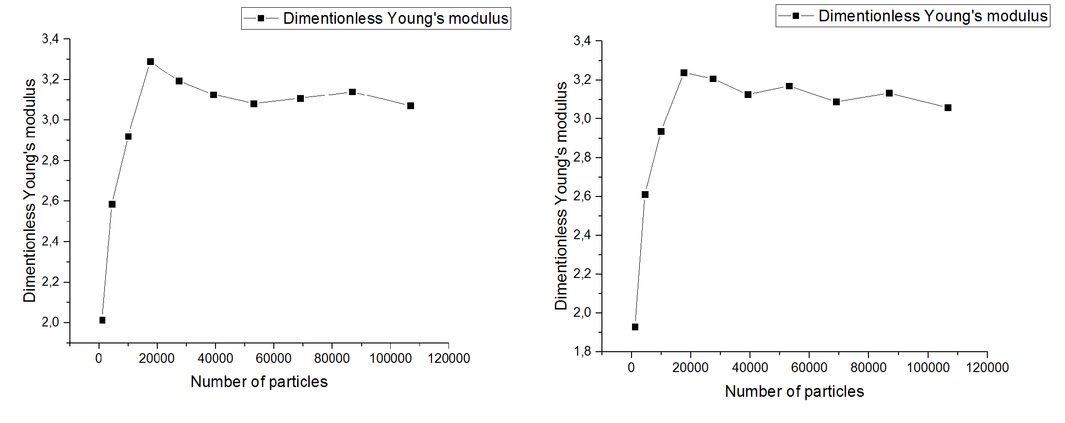
Исследованы зависимости механических характеристик материала со случайной упаковкой частиц от числа частиц.
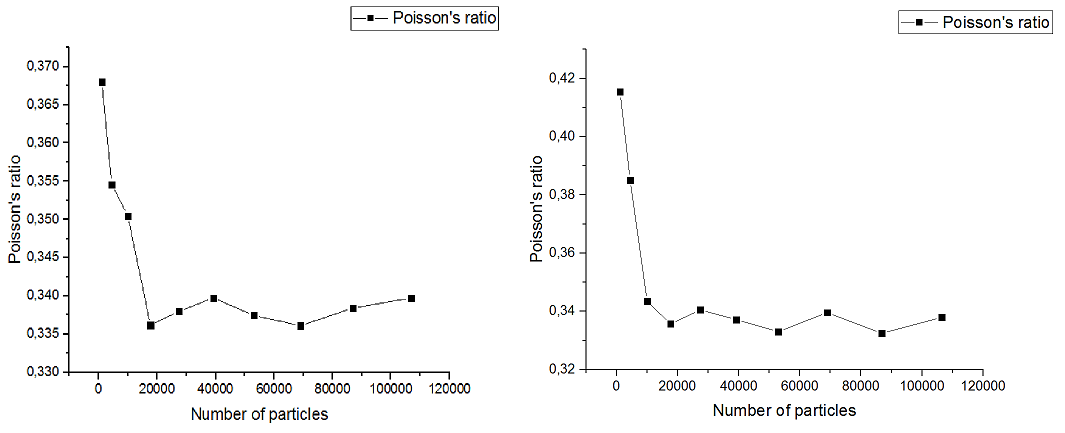
- Показано, что с увеличением числа частиц в упаковке сходятся такие характеристики материала, как модуль Юнга, коэффициент Пуассона.
- Коэффициент Пуассона, полученный для растяжения или сжатия упаковки вдоль оси y, различается на 0,5%, вдоль оси x на 0,3%. Значения коэффициента Пуассона для размеров упаковки 1000 и 10000 отличаются на 10%.
- При числе частиц в упаковке, равном 50*1000, можно считать, что были достигнуты предельные значения модуля Юнга и коэффициента Пуассона.
- Упругие свойства модели изотропны и одинаковы для растяжения и сжатия.
- Таким образом, удалось продемонстрировать cходимость механических характеристик созданной модели.