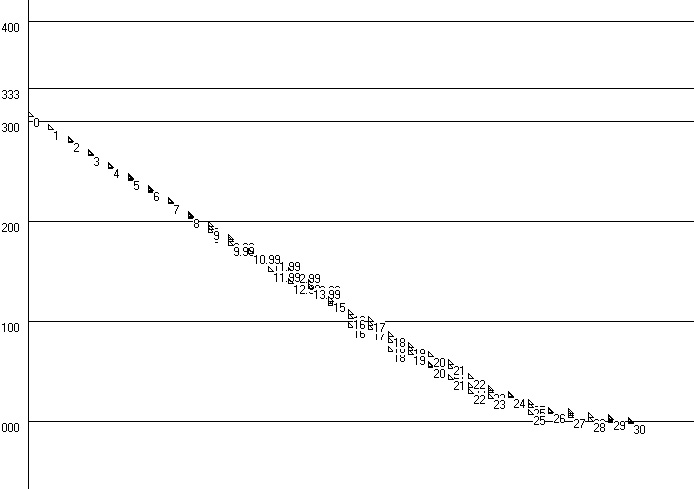
Модель растяжения материала

Цель исследования

Исследование коэффициента Пуассона модельного материала

Дано:

1. Модель материала - множество частиц, взаимодействующих друг с другом по определённому закону
2. Программа визуализации расчетных данных

Задача №1:

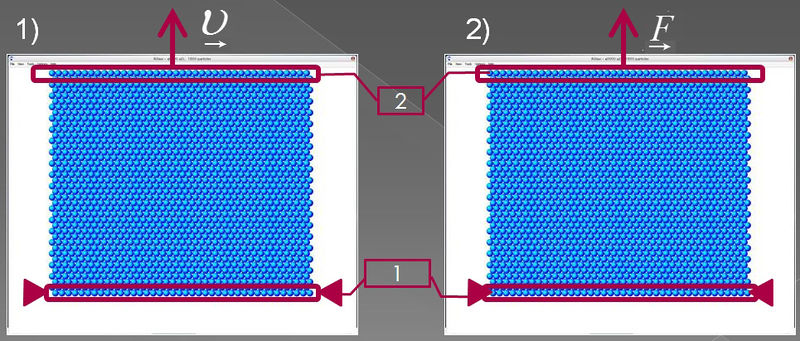
1. Сымитировать растяжение материала вдоль оси У
2. Сымитировать то же растяжение, только под действием фиксированной силы.

• 



Как взаимодействуют частицы

Взаимодействие частиц описывается потенциалом Леннарда-Джонса который записывается в следующем виде:
[math]U(r) = D \left[ \left(\frac{a}{r}\right)^{12} - \left(\frac{a}{r}\right)^{6} \right],[/math]
r — расстояние между центрами частиц
D  — глубина потенциальной ямы
a — равновесное расстояние
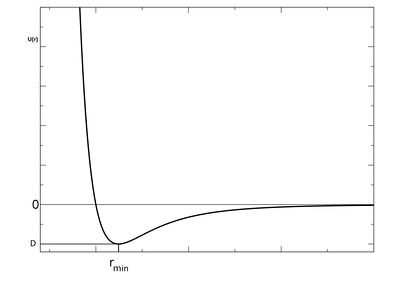
Параметры  D и a являются характеристиками вещества. Характерный вид потенциала показан на рисунке, его минимум лежит в точке [math]r_{min} = a[/math]

• 



Реализация на компьютере

Расчет силы взаимодействия частиц

[math]F = -U'(r)[/math]
[math]\b{F} = f_0\left[ \left(\frac{a}{r}\right)^{14} - \left(\frac{a}{r}\right)^{8}\right]\b{r}[/math]
[math]f_0 = 12\left(\frac{D}{a}\right)[/math]
Где D=1 , a=1 для данного материала , а [math]\b{r}[/math] – радиус-вектор, соединяющий 2 частицы

Расчет ускорения частицы (по II закону Ньютона)

[math]\b{a} = \b{F}/m[/math]
m – масса частицы, для данного материала m=1

Расчет скорости частицы

[math]\underline{\vartheta} = \underline{\vartheta}_{pre} +\underline{a}\cdot dt[/math]
[math]dt = \frac{1.45 \cdot T_0}{100}[/math] - шаг интегрирования
[math]T_0 = 2 \pi \sqrt{\frac{a}{6\cdot f_0}}[/math] - период колебаний частиц
[math]f_0[/math] – характерная сила межатомного взаимодействия

Расчет новых координат частицы

[math]\underline{r} = \underline{r}_{pre} + \underline{\vartheta} \cdot dt[/math]

Задача №2

Измерить коэффициент Пуассона для полученной модели
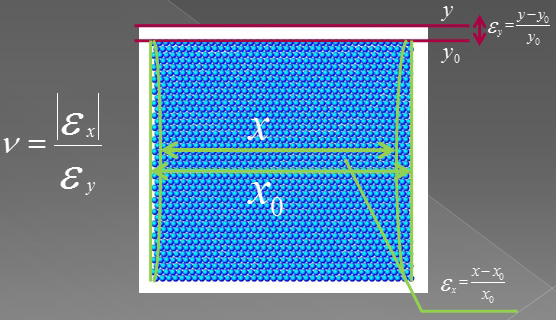
Коэффициент Пуассона - одна из физических характеристик материала упругого тела, равная отношению абсолютных значений относительной поперечной деформации элемента тела к его относительной продольной деформации.
Величина коэффициента Пуассона для большинства металлических материалов близка к 0,3.

• 



За начальное состояние материала взято его состояние на 1000м шаге. До него сила, растяжения материала = 0. Таким образом система уравновешивается. А уже начиная с этого шага мы нагружаем систему.

Результат: коэффициент Пуассона для модельного материала без пористости

В результате проделанной работы было определено, что для данной модели коэффициент Пуассона получился равным 0.33 ,что близко к результату, полученному аналитическим путем [math]\nu = \frac{1}{3}[/math]
[1]Кривцов А. М. Деформирование и разрушение твердых тел с микроструктурой. М.: ФИЗМАТЛИТ, (2007)

Другой способ расчета коэффициента Пуассона

Другой способ измерения основан на измерении напряжений возникающих в материале в напряженно-деформированном состоянии. И здесь вместо растяжения мы будем сжимать материал. Этим исключается искажение результатов вызванное разрывом материала. Также используются периодичные граничные условия (мы окружаем наш кусочек материала со всех сторон идентичными ему кусочками материала т.е. как только частица улетела вправо за границу рассматриваемой области то она прилетает с левой границы) таким образом создается эффект рассмотрения маленького участка вместо рассмотрения маленького кусочка материала как в предыдущем методе. Здесь мы деформируем материал не динамически прикладывая силу а уже изначально создаем деформированный материал зажатый границами рассматриваемой области.
В этом состоянии мы измеряем напряжения возникшие в рассматриваемом материале по вертикали и по горизонтали.
[math]C_e = \frac {F_e} {S}[/math]
[math]C_e[/math] — механическое напряжение вдоль оси [math]\underline{e}[/math]
[math]F_e[/math] — сила, возникшая в теле вдоль оси [math]\underline{e}[/math] при деформации
S — площадь. [math]\nu = \frac{C_x}{C_y}[/math]

Результаты

Без пористости

Используя этот метод удалось с высокой точностью (до [math]10^{-6}[/math]) получить значение коэффициента Пуассона для данного материала. [math]\nu =0.333333 \approx \frac{1}{3}[/math]
Что соответствует аналитическому результату.

Зависимость коэффициента Пуассона от пористости материала

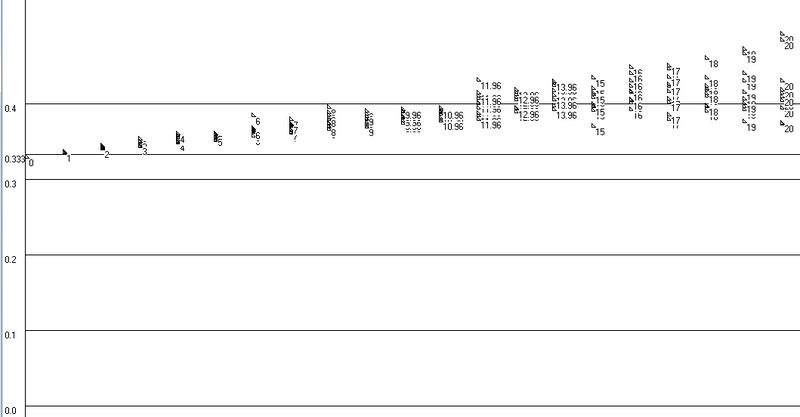
В материале было задано случайное распределение пустот(извлечен случайный набор частиц) и для разного процента пористости был измерен коэффициент Пуассона. Для каждого значения процента пористости делалось несколько измерений коэффициента Пуассона для разного распределения пустот. В результате чего был построен График Зависимости коэффициента Пуассона от пористости материала

• 



Как видно зависимость возрастающая что само по себе странно т.к. все экспериментальные(для пенобетона) и аналитические данные говорят обратное что зависимость должна быть убывающая. В результате долгих поисков ошибка не обнаружилась и было решено измерить зависимость модуля Юнга от пористости таким же способом и проверить что будет с ней...

Зависимость модуля Юнга от пористости материала

Зависимость оказалась убывающей что похоже на правду.
График зависимости модуля Юнга от пористости материала:

•