Модели Фоккера-Планка

Скорость убегания для изотермических систем

Одним из недостатков изотермических сфер состоит в том, что они бесконечны. Если бы не этот факт, то как простые модели они могли бы очень хорошо представлять реальные системы. Основным их достоинством является максвеловское распределение скоростей, поскольку именно такое распределение характеризует прорелаксировавшие системы. Для того, чтобы сделать сферу конечной, можно ввести свойственную конечным системам скорость убегания. Скорость убегания на границе изолированной системы зависит только от её полной массы [math]M[/math] и радиуса [math]R[/math]. Внутри системы локальная скорость убегания, т.е. скорость, необходимая для того, чтобы находящейся в некоторой внутренней точке [math]r[/math] объект мог покинуть систему будет зависеть от локального значения гравитационного потенциала [math]\Phi(r)[/math]. Поэтому в области значений [math]v\gt v_e[/math]функция распределения [math]f(r,v,t)[/math] очень близка к нулю ([math]v_e[/math] значение скорости убегания).

При этих условиях можно сделать интуитивное предположение о характере распределения скоростей. Это предположение оказывается верным в данной модели и его можно доказать более строго (см. Саслоу "Грав. физика звёздных и галакт. систем"). Усечённая функция распределения Максвелла имеет вид:

[math](1):f(v)=A(e^{-j^2 v^2}-B)[/math],

где [math]A[/math] и [math]B[/math] константы, [math]j[/math]-коэффециент дисперсии. С физической точки зрения [math]f(v)=0[/math] при [math]e^{-j^2 v^2} \le B[/math], и для того, чтобы это выполнялось, необходимо, чтобы [math]B=e^{-j^2 v_e^2}[/math]. Константу [math]A[/math] можно получить, производя нормировку таким образом, чтобы [math]f(v)=1[/math] при наиболее вероятном значении скорости [math]v=0[/math].

В результате имеем:

[math](2): f(v)=A\cdot(e^{-j^2 v^2}-e^{-j^2 v_e^2})=\frac{e^{-j^2 v^2}-e^{-j^2 v_e^2}}{1-e^{-j^2 v_e^2}}[/math]

Частица покинет пределы скопления, если её скорость превзойдёт значение [math]v_e[/math], которое зависит от положения в скоплении. Эта зависимость от радиуса войдёт и в функцию [math]f(r,v)[/math]. Энергия отдельной частицы:

[math](3): E=\frac{1}{2}v^2+\Phi(r)[/math]

Теперь оказывается удобным положить потенциал [math]\Phi(r)[/math] равным нулю на поверхности скопления, а не на бесконечности. При таком определении частица с нулевой полной энергией едва достигнет этой поверхности. Таким образом скорость убегания определяется равенством

[math](4): v_e^2=-2\Phi(r)[/math]

Подставляя значения скорости из уравнения (3) и скорости убегания из уравнения (4) в (2) можно получить уравнение функции распределения для любого радиуса

[math](5): f(r,v)=A e^{-2j^2(\Phi(r)-\Phi(0))}\cdot (e^{-j^2 v^2}-e^{-j^2 v_e^2})[/math]

Интегрируя функцию распределения по скоростям получаем плотность

[math](6): \rho(r)=\int_0^{v_e} f(r,v)4\pi v^2 dv=4\pi A e^{-2j^2(\Phi(r)-\Phi(0))}\int_0^{v_e} (e^{-j^2 v^2}-e^{-j^2 v_e^2})v^2 dv[/math]

как функцию потенциала [math]\Phi(r)[/math]

Чтобы получить однозначно [math]\rho(r)[/math] нужно воспользоваться уравнением Пуассона

[math]\frac{d^2 \Phi}{dr^2}+\frac{2}{r}\frac{d\Phi}{dr}=4\pi G\rho(\Phi)[/math]

Которое с учётом сдвига координат перепишется, как

[math](7): \frac{d^2 \Phi}{dr^2}+\frac{2}{r}\frac{d\Phi}{dr}=4\pi G\rho(\Phi(r))-4\pi G\rho(\Phi(R))[/math]

Потенциал во внутренней точке с радиус-вектором [math]r[/math] массивной сферы определяется выражением

[math](8): \Phi(r)=\frac{Gm(r)}{r}+4\pi G \int_r^R \rho(r') r' dr'-\frac{GM}{R}[/math],

где [math]m(r)=4 \pi \int_0^r r^2 \rho(r)dr[/math] -масса вложенной сферы сферы радиуса [math]r[/math], а "[math]-\frac{GM}{R}[/math]" появляется из-за сдвига "нуля" потенциала.

Потенциал на границе шара, по условию

[math](9):\Phi(R)=0[/math]

Потенциал в центре [math]r \to 0[/math]

[math](10): \Phi(0)=4\pi G \int_0^R \rho(r) r dr-\frac{GM}{R}[/math].

[math]\rho(r)= \rho(0) e^{-\theta(r)}[/math]

Незвестная функция [math]\theta(r)[/math] не позволяет вычеслить интеграл.

Плотность в центре сферы

Найдём значение плотности в центре шара. Из [math](6)[/math] имеем

[math](11): \rho(0)=4\pi A \int_0^{v_e} (e^{-j^2 v^2}-e^{-j^2 v_e^2})v^2 dv[/math]

Основную трудность здесь представляет интеграл

[math]\int_0^{v_e} e^{-j^2 v^2}v^2 dv[/math],

В Берклеевском курсе физике (т.5 стр 338) найдено значение интеграла на всей вещественной оси [math]\mathbf{R}[/math]:

[math] (12): \int_{-\infty}^{\infty} e^{-j^2 v^2}v^2 dv=\frac{\sqrt{\pi}}{2}j^{-3/2}[/math]

Значение же интеграла на произвольном отрезке не получить в элементарных функциях.

Можно пойти на хитрость.

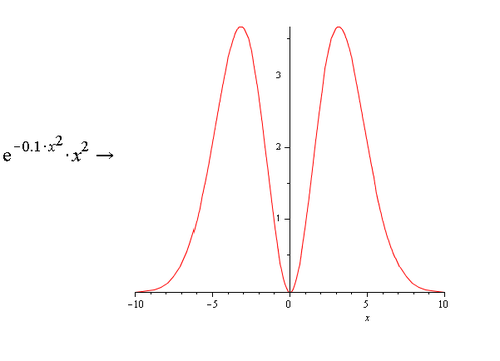
Экстремумы подынтегральной функции достигаются при [math]x=0[/math] и [math]x=\pm j^{-1}[/math] (рис. 1).

Если [math]v_e\ge 3\cdot j^{-1}[/math] (3-ка написана из-за несимметричности функции), то можно считать, что что значение такого интеграла приближённо равно половине интеграла [math](12)[/math].

рис. 1

Тогда, при выполнении предположения [math]v_e\ge 3\cdot j^{-1}[/math]:

[math](13): \rho(0)=4\pi A \int_0^{v_e(0)} e^{-j^2 v^2}\cdot v^2 dv-4\pi A \int_0^{v_e(0)} e^{-j^2 v_e(0)^2}\cdot v^2 dv=\pi^{3/2} Aj^{-3/2}-\frac{4}{3}\pi A v_e^2 e^{-j v_e(0)^2}[/math]