Моделирование течения жидкости при сжатии канала в одном направлении и удлинении в другом
Материал из Department of Theoretical and Applied Mechanics
Курсовые работы 2016-2017 учебного года > Моделирование течения жидкости при сжатии канала в одном направлении и удлинении в другом (elongation flow) методом динамики частиц
Курсовой проект по Механике дискретных сред
Исполнитель: Мущак Никита
Группа: 09 (43604/1)
Семестр: осень 2016
Описание задачи[править]
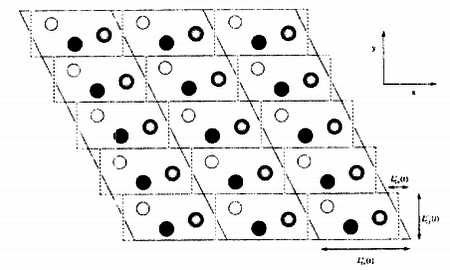
Моделирование течения жидкости при сжатии канала в одном направлении и удлинении в другом (elongational flow) было произведено методом динамики частиц. Каждая частица представляет собой абсолютно упругий шар. Взаимодействие между шарами описывается потенциалом Леннарда-Джонса. Моделирование данного течения производиться в помощью периодических граничных условий Крайника-Реинельта (Kraynik-Reinelt). При которых боковые границы ячейки периодичности поворачиваются, относительно вертикального положения (Рис.1).
Ниже привеведен код граничных периодических условий Крайника-Реинельта:
Где и - это координаты частицы, и - ширина и высота ячейки периодичности. и - смещение по x b y при переходе через границы ячейки периодичности.
Программа[править]
Текст программы на языке JavaScript:
Файл "NNNN.js"
1 function main_particle_1(canvas_particle_1,slider_01) {
2 // Предварительные установки
3 var w_1 = canvas_particle_1.width; // Ширина рабочего поля
4 var h_1 = canvas_particle_1.height; // Высота рабочего поля
5
6 var w = w_1/3; // Ширина ячеки периодичности
7 var h = h_1/3;
8
9 var ctx = canvas_particle_1.getContext("2d");
10
11 this.newSystem = function() {
12 var w_1 = canvas_particle_1.width; // Ширина рабочего поля
13 var h_1 = canvas_particle_1.height; // Высота рабочего поля
14
15 var w = w_1 / 3; // Ширина ячеки периодичности
16 var h = h_1 / 3; // Высота ячейки периодичности
17 };
18 var sh = -10 * 15;
19 // Наклоненность боковых границ ячеек ее можно менять
20 this.set_01 = function(o) {sh = 10 * o;};
21
22 // настройка слайдеров и текстовых полей
23 slider_01.min = -15; slider_01.max = 15;
24 slider_01.step = 1;
25 slider_01.value = sh/10; // начальное значение ползунка должно задаваться после min и max
26 text_01.value = sh/10;
27
28 var s = 0; // предустановка
29 var s1 = 2/3 * sh; // Начальный сдвиг при переходе через гориз. границу
30 var se = -(2 * sh / h_1) * (h - 0.5 * h_1); // Начальный сдвиг при переходе через верт. границу
31 var r = 10; // Радиус частиц
32 var N = 10; // Число частиц можно менять
33 rx = new Array(); // Содержит координаты частиц по оси Х
34 ry = new Array(); // Содержит координаты частиц по оси У
35 rxI0 = new Array(); // Координаты для ячеек перидичностей - клонов
36 rxI1 = new Array();
37 rxI2 = new Array();
38 rxI3 = new Array();
39 rxI4 = new Array();
40 rxI5 = new Array();
41 rxI6 = new Array();
42 rxI7 = new Array();
43 ryI0 = new Array();
44 ryI1= new Array();
45 ryI2= new Array();
46 ryI3= new Array();
47 ryI4= new Array();
48 ryI5= new Array();
49 ryI6= new Array();
50 ryI7= new Array();
51 vx = new Array(); //Скорость по Х
52 vy = new Array(); //Скорость по У
53 vx_p = new Array();vx_m = new Array();vy_p = new Array();vy_m = new Array();
54 var distR0,distR2,distR3,distR;
55
56 L = new Array(); // Кинетический момент
57 var D = 5; // Энергия связи
58 var a0 = w * 0.1;
59 var c = 72 * D/r; // Жесткость связи частиц
60 var W = Math.sqrt(c);
61 var T = 2 * Math.PI/W;
62 dt = 0.03;
63 //0.04380741654852822
64
65
66
67
68 for (i = 0; i < N/2; ++i)
69 {
70 vx_p[i] = Math.random()*15;
71 vy_p[i] = Math.random()*15;
72 vx_m[i] = Math.random()*15;
73 vy_m[i] = Math.random()*15;
74 vx = vx_p.concat(vx_m);
75 vy = vy_p.concat(vy_m);
76 }
77
78 var kol = 1;
79 var prx = 0;
80 var pry = 0;
81 var dist= 0;
82 var f;
83 rx[0] = Math.random() * (w - 10) ;//-s;
84 ry[0] = Math.random() * (h - 10);
85 while (kol < N)
86 {
87 f = 0;
88 prx = Math.random() * (w - 10);//-s;
89 pry = Math.random() * (h - 10);
90 for (i = 0; i < kol; i++)
91 {
92 dist = Math.pow((rx[i] - prx),2) + Math.pow((ry[i] - pry),2);
93 if (dist < Math.pow(2 * a0,2))
94 {
95 f = f+1;
96 }
97 }
98 if (f==0)
99 {
100 rx[kol] = prx;
101 ry[kol] = pry;
102 kol++;
103 }
104 }
105
106 var steps = 0;
107
108
109 function step()
110 {
111 tick();
112 draw();
113 }
114 var vGraph = new TM_graph( // определить график
115 "#vGraph", // на html-элементе #vGraph
116 1000, // сколько шагов по оси "x" отображается
117 -1, 1,0.2); // мин. значение оси Y, макс. значение оси Y, шаг по оси Y
118
119 function tick()
120 {
121 for (i = 0; i < N ; i++)
122 {
123
124 steps += 1;
125
126 rx[i] += vx[i]*dt;
127 ry[i] += vy[i]*dt;
128
129 s = -(2 * sh / h_1) * (ry[i] - 0.5 * h_1);
130
131 if (rx[i] >= w - s) {rx[i] = rx[i] - w ;}
132 if (rx[i] <= 0 - s) {rx[i] = rx[i] + w;}
133
134 if (ry[i] >= h) {ry[i] = ry[i] - h ;
135 rx[i]=rx[i]- 2 * se; }
136 if (ry[i] <= 0) {ry[i] = ry[i] + h;
137 rx[i]=rx[i]+2*se; }
138
139 rxI0[i] = rx[i] + w;
140 ryI0[i] = ry[i];
141
142 rxI3[i] = rx[i] + w +s1;
143 ryI3[i] = ry[i] + h;
144
145 rxI6[i] = rx[i] + w +s1 +s1;
146 ryI6[i] = ry[i] + 2*h;
147
148 rxI1[i] = rx[i] + 2*w ;
149 ryI1[i] = ry[i];
150
151 rxI4[i] = rx[i] + 2*w +s1;
152 ryI4[i] = ry[i] + h;
153
154 rxI7[i] = rx[i] + 2*w +s1 +s1 ;
155 ryI7[i] = ry[i] + 2*h;
156
157 rxI2[i] = rx[i] +s1;
158 ryI2[i] = ry[i] + h;
159
160 rxI5[i] = rx[i] +s1 +s1 ;
161 ryI5[i] = ry[i] + 2*h;
162
163
164
165 //раcсчет расстояний
166
167 for (j = 0; j < N ; j++)
168 {
169 if (i != j)
170 {
171 distR0 = Math.sqrt(Math.pow((rx[i]-rxI0[j]),2)+Math.pow((ry[i]-ryI0[j]),2));
172 distR2 = Math.sqrt(Math.pow((rx[i]-rxI2[j]),2)+Math.pow((ry[i]-ryI2[j]),2));
173 distR3 = Math.sqrt(Math.pow((rx[i]-rxI3[j]),2)+Math.pow((ry[i]-ryI3[j]),2));
174 distR = Math.sqrt(Math.pow((rx[i]-rx[j]),2)+Math.pow((ry[i]-ry[j]),2));
175
176 //раcсчет сил
177 a = 4 * r;
178 if (distR0 < 2*r)
179 {
180 var mod_fR0,fxR0,fyR0;
181
182 mod_fR0 = 12*D*((Math.pow(r/distR0),13)-Math.pow((r/distR0),7))/a;
183 //console.log(mod_fR0);
184 if (mod_fR0 >=0)
185 {
186 fxR0 = mod_fR0*(rx[i]-rxI0[j]);
187 fyR0 = mod_fR0*(ry[i]-ryI0[j]);
188 vx[i]+=fxR0*dt;
189 vx[j]-=fxR0*dt;
190 vy[i]+=fyR0*dt;
191 vy[j]-=fyR0*dt;
192 }
193 }
194 if (distR2 < 2*r)
195 {
196 var mod_fR2,fxR2,fyR2;
197
198 mod_fR2 = 12*D*((Math.pow(r/distR2),13)-Math.pow((r/distR2),7))/a;
199
200 if (mod_fR2 >=0)
201 {
202 fxR2 = mod_fR2*(rx[i]-rxI2[j]);
203 fyR2 = mod_fR2*(ry[i]-ryI2[j]);
204 vx[i]+=fxR2*dt;
205 vx[j]-=fxR2*dt;
206 vy[i]+=fyR2*dt;
207 vy[j]-=fyR2*dt;
208 }
209 }
210 if (distR3 < 2*r)
211 {
212 var mod_fR3,fxR3,fyR3;
213
214 mod_fR3 = 12*D*((Math.pow(r/distR3),13)-Math.pow((r/distR3),7))/a;
215
216 if (mod_fR3 >=0)
217 {
218 fxR3 = mod_fR3*(rx[i]-rxI3[j]);
219 fyR3 = mod_fR3*(ry[i]-ryI3[j]);
220 vx[i]+=fxR3*dt;
221 vx[j]-=fxR3*dt;
222 vy[i]+=fyR3*dt;
223 vy[j]-=fyR3*dt;
224 }
225 }
226
227 if (distR < 2*r)
228 {
229 var mod_fR,fxR,fyR;
230 mod_fR = 12*D*((Math.pow(r/distR),13)-Math.pow((r/distR),7))/a;
231 if (mod_fR >=0)
232 {
233 fxR = mod_fR*(rx[i]-rx[j]);
234 fyR = mod_fR*(ry[i]-ry[j]);
235 vx[i]+=fxR*dt;
236 vx[j]-=fxR*dt;
237 vy[i]+=fyR*dt;
238 vy[j]-=fyR*dt;
239 }
240 }
241
242 Array.prototype.sum = function()
243 {
244 for (var i=0, sum=0; i < this.length; sum += this[i++]);
245 return sum;
246 }
247
248
249 // L[i] = (rx[i] * vy[i] - ry[i] * vx[i])/6000;
250 var sumL = L.sum();
251 //график
252 // if (steps % 50 == 0) vGraph.graphIter(steps, sumL); // подать данные на график
253 //console.log(sumL);
254
255 }
256
257 }
258 }
259 }
260
261
262 function draw()
263 {
264 ctx.clearRect(0, 0, w_1+100 , h_1+100); // очистить экран
265 for (var i = 0; i < N; i++)
266
267 {
268 var x = rx[i];
269 var y = ry[i];
270 ctx.beginPath();
271 ctx.fillStyle = "#00008B";
272 ctx.arc(x, y, r , 0, 2 * Math.PI, false);
273 ctx.closePath();
274 ctx.fill();
275
276 var xI0 = rxI0[i];
277 var yI0 = ryI0[i];
278 ctx.beginPath();
279 ctx.fillStyle = "#00008B";
280 ctx.arc(xI0, yI0, r , 0, 2 * Math.PI, false);
281 ctx.closePath();
282 ctx.fill();
283
284 var xI1 = rxI1[i];
285 var yI1 = ryI1[i];
286 ctx.beginPath();
287 ctx.fillStyle = "#00008B";
288 ctx.arc(xI1, yI1, r , 0, 2 * Math.PI, false);
289 ctx.closePath();
290 ctx.fill();
291
292 var xI2 = rxI2[i];
293 var yI2 = ryI2[i];
294 ctx.beginPath();
295 ctx.fillStyle = "#00008B";
296 ctx.arc(xI2, yI2, r , 0, 2 * Math.PI, false);
297 ctx.closePath();
298 ctx.fill();
299
300 var xI3 = rxI3[i];
301 var yI3 = ryI3[i];
302 ctx.beginPath();
303 ctx.fillStyle = "#00008B";
304 ctx.arc(xI3, yI3, r , 0, 2 * Math.PI, false);
305 ctx.closePath();
306 ctx.fill();
307
308 var xI4 = rxI4[i];
309 var yI4 = ryI4[i];
310 ctx.beginPath();
311 ctx.fillStyle = "#00008B";
312 ctx.arc(xI4, yI4, r , 0, 2 * Math.PI, false);
313 ctx.closePath();
314 ctx.fill();
315
316 var xI5 = rxI5[i];
317 var yI5 = ryI5[i];
318 ctx.beginPath();
319 ctx.fillStyle = "#00008B";
320 ctx.arc(xI5, yI5, r , 0, 2 * Math.PI, false);
321 ctx.closePath();
322 ctx.fill();
323
324 var xI6 = rxI6[i];
325 var yI6 = ryI6[i];
326 ctx.beginPath();
327 ctx.fillStyle = "#00008B";
328 ctx.arc(xI6, yI6, r , 0, 2 * Math.PI, false);
329 ctx.closePath();
330 ctx.fill();
331
332 var xI7 = rxI7[i];
333 var yI7 = ryI7[i];
334 ctx.beginPath();
335 ctx.fillStyle = "#00008B";
336 ctx.arc(xI7, yI7, r , 0, 2 * Math.PI, false);
337 ctx.closePath();
338 ctx.fill();
339
340 }
341 ctx.beginPath(); // начать рисование
342 ctx.fillStyle="#000000";
343 ctx.moveTo(w-sh, 0); // переместить "карандаш" в точку
344 ctx.lineTo(w+sh, h_1); // нарисовать "карандашом" линию до точки
345 ctx.stroke();
346
347 ctx.beginPath();
348 ctx.fillStyle="#000000";
349 ctx.moveTo(2 * w-sh, 0);
350 ctx.lineTo(2 * w+sh, h_1);
351 ctx.stroke();
352
353 ctx.beginPath();
354 ctx.fillStyle="#000000";
355 ctx.moveTo( 0- sh, 0);
356 ctx.lineTo( sh, h_1);
357 ctx.stroke();
358
359 ctx.beginPath();
360 ctx.fillStyle="#000000";
361 ctx.moveTo(w_1 - sh, 0);
362 ctx.lineTo(w_1 + sh, h_1);
363 ctx.stroke();
364
365 ctx.beginPath();
366 ctx.fillStyle="#000000";
367 ctx.moveTo(0, h);
368 ctx.lineTo(w_1, h);
369 ctx.stroke();
370
371 ctx.beginPath();
372 ctx.fillStyle="#000000";
373 ctx.moveTo(0, 2 * h);
374 ctx.lineTo(w_1, 2 * h);
375 ctx.stroke();
376 }
377 // Запуск системы
378 this.newSystem();
379 setInterval(step, 1000/120); // функция step будет запускаться 60 раз в секунду (60 раз / 1000 мс)
380
381 }
Ссылки по теме[править]
- Danis J. Evans, Garry Morriss "Statitical mechanics of nonequilibrium liquids", 2008, pages 146-150.
- A. M. KRAYNIK and D. A. REINELT "EXTENSIONAL MOTIONS OF SPATIALLY PERIODIC LATTICES ",1992.
- B. D. Todd, Peter J. Daivis "Nonequilibrium Molecular Dynamics Simulations of Planar Elongational Flow with Spatially
and Temporally Periodic Boundary Conditions", 1992.
- B.D.Todd, Peter J. Daivis "New algorithm for unrestricted duration nonequilibrium molecular dynamics
