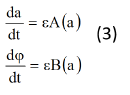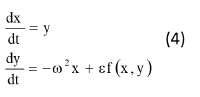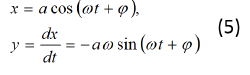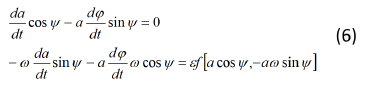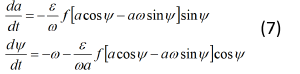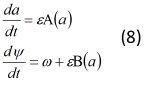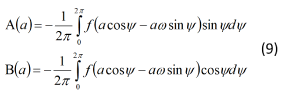Метод Ван-дер-Поля

Цель курсового проекта

Задачей данной работы является сравнение прямого решения и метода Ван-дер-Поля приближённого решения уравнения.

Описание метода

В своих исследованиях Ван-дер-Поль рассматривал уравнения с малым положительным параметром ε

Оно описывает колебательные движения в среде низкого трения.Уравнение (1) называют квазилинейным, а колебания соответственно квазилинейными. Функция f может быть весьма различной, но мы будем рассматривать в виде (1а).

Уравнение

называется порождающим и описывает обычные гармонические колебания. Общее решение записывается в виде:

х=acos(ωt+φ)

Ван-дер-Поль предложил, что приближённое решение уравнения (1) можно представить так же как и решение уравнения (2), только с изменяющимися амплитудой а и фазой φ, этот метод был назван методом «Медленно меняющихся коэффициентов». Которые находятся из системы дифференциальных уравнений с разделяющимися переменными.

Уравнения (3), так называемые «укороченные уравнения» Ван-дер-Поля, позволяют сравнительно просто получить приближенное решение исходного уравнения (1). Перейдем к составлению «укороченных уравнений» для рассматриваемого уравнения (1), или эквивалентной ему системы двух уравнений первого порядка

Прежде всего, заметим, что при ε=0 уравнение (1) превращается в дифференциальное уравнение обычного гармонического осциллятора, и тогда решение системы (4) имеет вид:

где а и φ— постоянные интегрирования.

Будем отыскивать решение уравнения (4) при достаточно малых значениях параметра ε в виде выражений (5), но уже считая а и φ не постоянными, а некоторыми функциями времени. Для этого будем рассматривать выражения (5) не как решения уравнения (4) при ε = 0, а как формулы замены старых переменных х и у на новые переменные а и φ.

Сделаем замену:

Продифференцировав выражения (5) по t, подставим значения производных в уравнениях (4).

Разрешая систему (6) относительно da/dt и Ψ , находим систему уравнений:

Система дифференциальных уравнений (7) эквивалентна рассматриваемой исходной системе (4). Из системы (7) видно, что медленные и быстрые движения для Ψ разделены. Усредняя правые части системы (7) мы получим:

Где A(a) и B(a) имеют вид:

Уравнения (8) будем называть укороченными уравнениями или уравнениями Ван-дер-Поля. Они значительно проще исходной системы (7), поскольку первое уравнения может быть проинтегрировано независимо от второго. В системе (8) медленные и быстрые движения для разделены. Интегрируя первое из уравнений этой системы, мы находим закон изменения амплитуды. Очень часто в прикладных задачах бывает достаточно найти только зависимость амплитуды от времени.

Итак, метод Ван-дер-Поля решения уравнения (1) состоит в переходе от переменной х и y к переменным а и (которые мы будем называть переменными Ван-дер-Поля) и к замене точных уравнений (7) укороченной системой (8).

В заключении стоит заметить, что метод Ван-дер-Поля хорошо работает только при малых параметрах ε

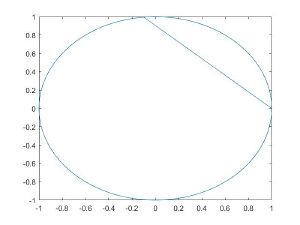
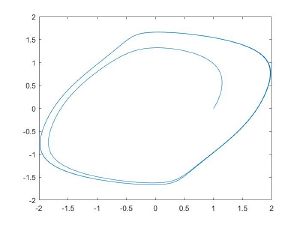
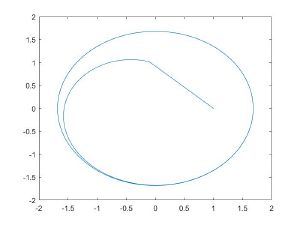
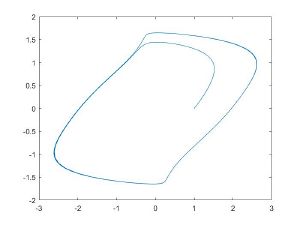
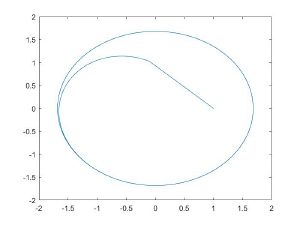
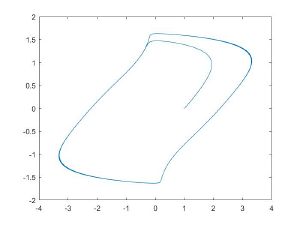
Фазовые портреты

С помощью пакета Matlab были построены фазовые портреты для метода Ван-дер-Поля и приближенного численного метода решения при различных параметрах ε.

Метод Ван-дер-Поля	Численное решение
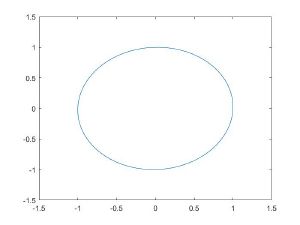
ε = 0
ε = 0,2
ε = 0,5
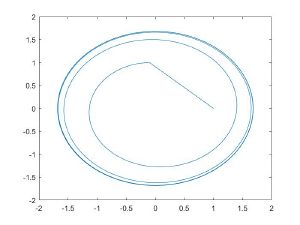
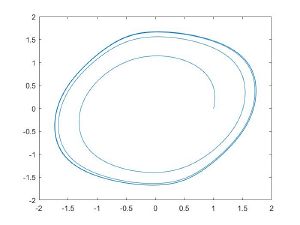
ε = 1	Текст ячейки
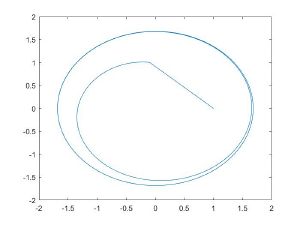
ε = 1,5	Текст ячейки

Листинг кода

Код Matlab:

Метод Ван-дер-Поля(vanDP.m)

x = zeros(1,d);
n = 10;
h = 2*pi/n;
x(1) = 0;
y(1) = 1;
a = sqrt((x(1))^2+(y(1)/w)^2);

for j = 2:d
  A=0;
  B=0;
   for i = 1:n
      A = A + (1-(a*cos(2*pi*i/n))^4)*(sin(2*pi*i/n))^2*h;
      B = B + (1-(a*cos(2*pi*i/n))^4)*sin(2*pi*i/n)*cos(2*pi*i/n)*h;
   end;
  da = A*eps*a*w/(2*pi);
  w = w + B*eps*a*w/(2*pi);
  a = a + da*dt
  t = dt*j;
  x(j) = a*cos(w*t + phi);
  y(j) = -w*a*sin(w*t + phi);
end; 
figure;
plot(y,x);

Численное решение

eps = 1.5;
w = 1;
n = 10000;
dt = 0.05;
y = zeros(1,n);
x = zeros(1,n);
Dy = zeros(1,n);
x(1) = 0;
y(1) = 1;
for i = 2:n
  Dy(i) = eps*(1-(x(i-1))^4)*y(i-1)-w^2*x(i-1);
  y(i) = Dy(i)*dt + y(i-1);
  x(i) = y(i)*dt + x(i-1);
end;
figure;
plot(y,x);

Работу выполнил

Уманский Александр