Кривчиков А.В.: Исследование прочности агломератов AL2O3 при статической и динамической нагрузках

Работу выполнил студент кафедры "Теоретическая механика" Кривчиков Аркадий (Группа 04).

Описание

Данная работа выполнена в рамках Гамбургского проекта при поддержке стипендиальной программы "Леонард Эйлер" немецкой службы академических обменов (DAAD).

Руководители

Руководитель со стороны СПбГПУ: к.ф.-м.н И.Е. Беринский

Руководители со стороны TUHH: Dipl.-Ing. S. Kozhar, Prof. Dr.-Ing. S. Antonyuk

Аннотация

Агломератами называют достаточно прочные соединения гранулируемого материала, обладающего пластичностью, т.е. такие соединения, которые могут подвергаться пластической деформации, не рассыпаясь на исходные зерна. Агломераты являются продуктом процесса агломерирования, одного из способов реализации процесса гранулирования.

Соответственно для лучшего понимания природы агломерата, необходимо изучить процесс гранулирования. Гранулированием называют совокупность физико-химических и физико-механических процессов, обеспечивающих формирование частиц определенных размеров, формы, структуры и физических свойств. Существует несколько способов исполнения процесса гранулирования: окатывание, спекание, прессование и, соответственно, агломерирование. На рисунке 1 представлены продукты, полученные при различных технологиях гранулирования.

Рис. 1. Гранулы при различной технологии производства

Данная работа выполнялась как часть большого проекта института твердых частиц SPE гамбургского технического университета TUHH. Целью настоящей работы является сбор информации для физического моделирования процессов окатывания и агломерирования: выявление напряжений, возникающих в мостике агломерата при статической и динамической нагрузках, выявление влияния геометрии мостика на прочность агломерата, выявление зависимости возникающих в мостике напряжений от угла падения и скорости удара агломерата о стенку гранулятора. Для достижения поставленных целей, были построены численные модели в инженерном программном комплексе ABAQUS, были произведены статические расчеты для различных геометрий мостика и динамическое расчеты для разных углов и скоростей падения на стенку гранулятора. Также было произведено сравнение напряжений в мостике агломерата при статической нагрузке с приближенной моделью балки Тимошенко.

Модель статичного нагружения агломерата

В лабораторных условиях реализация модели нагружения агломерата, состоящего из двух частиц затруднительна. Ввиду этого научными сотрудниками института твердых частиц (SPE) гамбургского технического университета (TUHH) была предложена идея численного расчета напряжений в мостике агломерата при использовании инженерного программного комплекса ABAQUS.

При создании CAE модели для расчета на прочность агломерата приняты следующие основные положения и допущения:

1. Используются линейно-упругие элементы.

2. Две частицы порошкообразного материала моделируются недеформирующимися сферами.

3. Межчастичная связь моделируется твердофазным мостиком с заданными свойствами полимера (Полиэтиленгликоля).

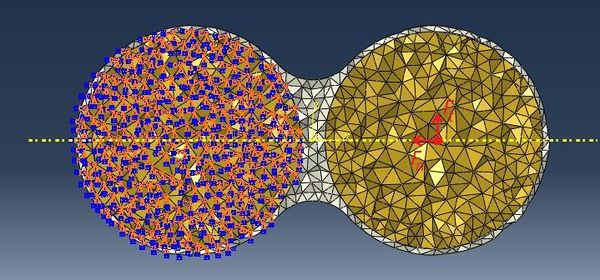
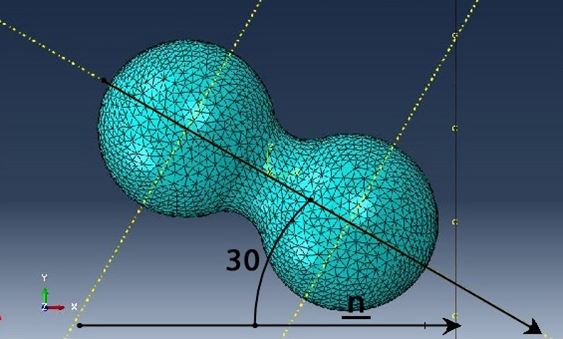
4. Конечно-элементная сетка (рис. 3.) строится из соотношения 1/10000, т.е. один элемент занимает не более 10000 части от общего объема.В качестве типа конечных элементов выбран тетраэдр. Такой тип элементов, наилучшим образом описывает объемы сферических форм.

5. На одну из частиц наложены ограничения трансляционного и вращательного движений.

6. К центру масс другой приложены тангенциальная и нормальная нагрузки относительно оси симметрии агломерата (рис. 2)

7. Граничные условия соединения материалов определены как жесткий контакт.

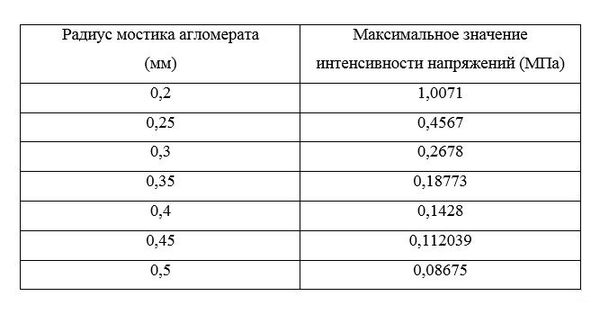
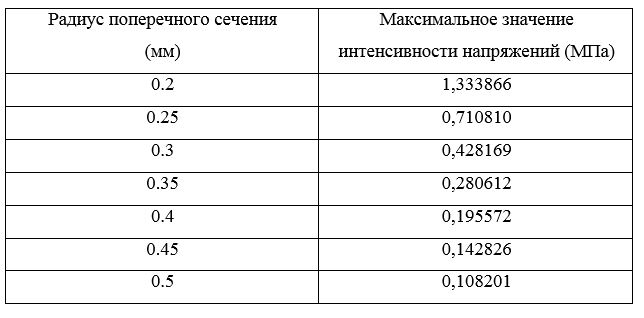
8. В качестве вариационного параметра выбран радиус мостика агломерата [math] R_b [/math]. Данный параметр изменяется в пределах от 0.2 мм до 0.5 мм. (Как свидетельствуют данные экспериментов, полученных институтом твердых частиц (SPE) гамбургского технического университета (TUHH), радиус мостика агломерата редко выходит за пределы таких значений).

Рис. 2. Конечно-элементная модель агломерата

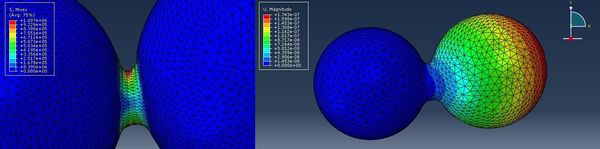
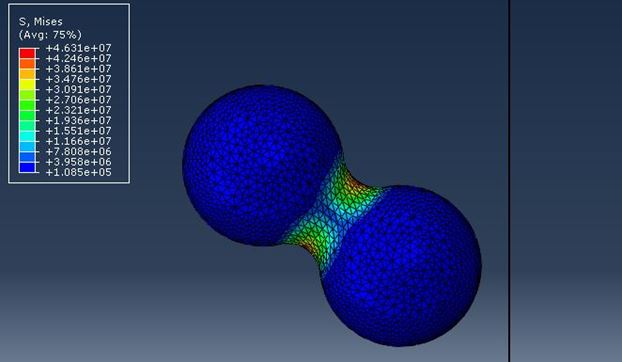
В результате проведения расчетов для заданных CAE-моделей агломерата были получены поля перемещений и напряжений. Пример поля напряжений и поля перемещений представлен на рис. 3. Максимальные значения напряжений, зарегистрированные в мостиках агломератов внесены в таблицу 1.

Рис. 3. Поля напряжений и перемещений соответственно

Таблица. 1. Результаты расчетов максимальных значений интенсивности напряжений, возникающих в мостике агломерата при статической нагрузке для разных радиусов мостика

Аналитическая модель балки Тимошенко

В качестве аналитической модели изгиба мостика агломерата была выбрана балка Тимошенко. Данная модель позволяет провести анализ влияния характерной геометрии мостика агломерата на возникающие в нем напряжения.

Постановка задачи

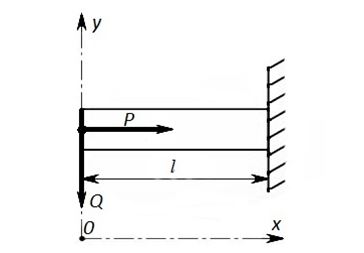
Рассмотрим балку с радиусом сечения [math] R [/math] и длинной [math] l [/math] (рис. 4). На торце [math] x=0 [/math] распределены касательные усилия, имеющие результирующую [math] Q=8 mN [/math] и нормальные усилия, имеющие результирующую [math] P=20 mN [/math].

Рис. 4. Модель балки с приложенными нагрузками

Уравнения равновесия для балки примут вид:

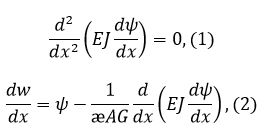
где [math] w [/math] – прогиб балки, [math] ψ [/math] – угол поворота сечения, [math] A [/math] – площадь сечения, [math] J [/math] – момент инерции сечения, [math] E [/math] – модуль Юнга, [math] G [/math] – модуль сдвига.

Граничные условия при x=0:

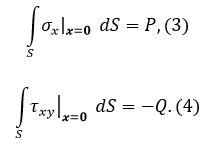
Граничное условие при x= l:

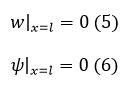
Параметры балки:

• Модуль Юнга [math] E = 2 GPa [/math];

• Коэффициент Пуассона [math] υ = 0.4 [/math];

• Длина балки [math] l= 0,9 mm [/math];

• Радиусы балки: [math] r = 0,2; 0,25; 0,3; 0.35; 0,4; 0,45; 0,5 mm [/math].

Общее решение:

Значение сжимающего напряжения принимается однородным во всём теле и равным:

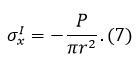
Данное решение удовлетворяет граничному условию (3).

Задача об изгибе балки решается с граничными условиями:

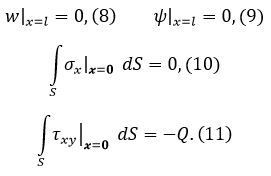
Решением задачи об изгибе будет:

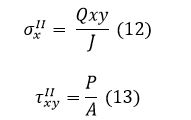
Где [math] J=πd^4/64=πr^4/4 [/math].

Общее решение имеет вид:

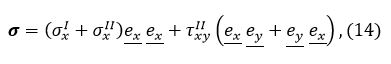
Интенсивность напряжений по Мизесу имеет вид:

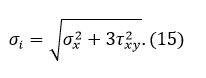
Максимальные значения интенсивности напряжений будут при [math] y = -r [/math] и [math] x = l[/math]

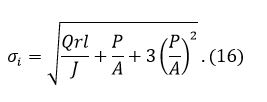
Результаты частного решения представлены в таблице 2.

Таблица. 2. Результаты аналитического расчета балки Тимошенко, зависимость максимального значения интенсивности напряжений от радиуса поперечного сечения балки.

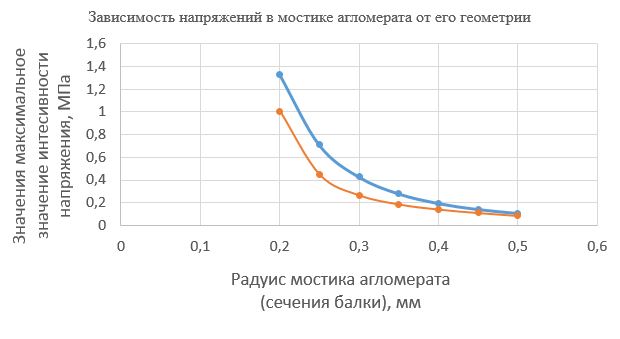
Далее представлен график сравнения результатов, полученных при численном моделировании с результатами аналитического решения балки Тимошенко

График 1. Сравнение результатов, полученных при численном моделировании и аналитическом решении.

Как видно из графика 1, кривые зависимости напряжений от радиуса имеют вид функции [math] 1/r^2 [/math] и совпадают с точностью до коэффициента. Отсюда выдвигается предположение, что появление такого коэффициента может быть связано непосредственно с характерной особенностью геометрии мостика.

Модель динамического нагружения агломерата

В продолжение работы по расчету напряжений в мостиках агломератов, научными сотрудниками института твердых частиц (SPE) гамбургского технического университета (TUHH) была поставлена задача численного расчета удара агломерата о стенку гранулятора. В рамках данного расчета существует задача определения напряжений в мостике агломерата, при различных скоростях и углах падения. Для данных целей, также использовался программный комплекс ABAQUS.

Основные положения и допущения, принятые при расчете удара агломерата о стенку гранулятора:

1. Используются линейно-упругие элементы.

2. Две частицы порошкообразного материала моделируются сферами с заданными свойствами оксида алюминия [math] Al_2 O_3 [/math]:

• Плотность [math] p = 1040 kg/m^3 [/math];

• Модуль Юнга [math] E = 14.5 GPa [/math] ;

• Коэффициент Пуассона [math] ν = 0.25 [/math].

3. Межчастичная связь моделируется твердофазным мостиком с заданными свойствами полимера (Полиэтиленгликоля)

• Плотность [math] ρ = 1000 kg/m^3 [/math];

• Модуль Юнга [math] E = 2 GPa [/math];

• Коэффициент Пуассона [math] ν = 0.4 [/math].

4. Конечно-элементная сетка (рис. 5.) строится из соотношения 1/10000, т.е. один элемент занимает не более 10000 части от общего объема.

5. Граничные условия соединения материалов были определены как жесткий контакт.

6. Граничное условие взаимодействия поверхности агломерата и стенки было определено с учетом сил трения (коэффициент трения κ=0.163).

7. В качестве вариационных параметров были выбраны скорость агломерата при ударе о стенку и угол падения.

8. В качестве 3D-CAD-модели агломерата, выбрана модель с радиусом мостика 0,5 мм.

Характерные размеры модели агломерата:

• Радиус частицы: [math] R_p=1.8 mm [/math];

• Толщина полимерного покрытия на частице [math] H_p=0.05 mm [/math] ;

• Длина мостика [math] L_b=0.2 mm [/math];

• Радиус мостика: [math] R_b=0.5 mm [/math].

Рис. 5. Конечно-элементная модель удара агломерата о стенку гранулятора под углом [math] 30^o [/math]

Результаты расчетов удара агломерата:

В результате проведения расчетов получены модели движения агломерата при ударе о стенку гранулятора и динамические поля напряжений. Пример поля напряжений представлен на рис. 6.

Рис. 6. Поле напряжений, возникающих в мостике агломерата при ударе о стенку гранулятора под углом [math] 30^o [/math]

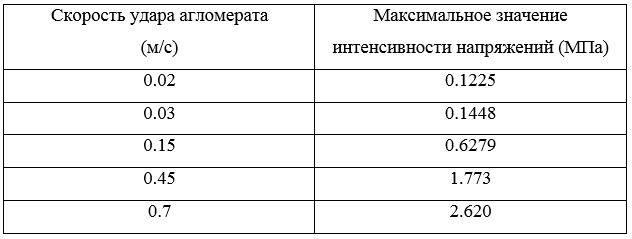
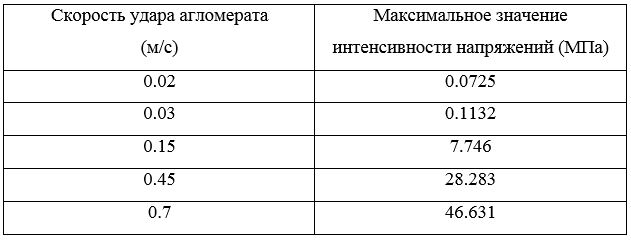
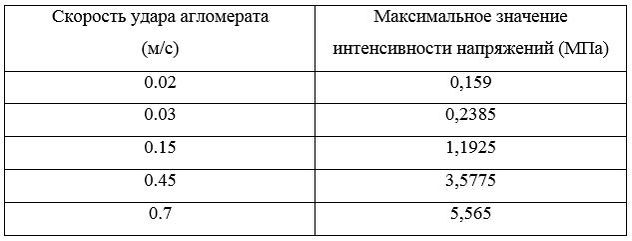
Максимальные значения напряжений, зарегистрированных в мостике агломерата внесены в таблицы 3, 4 и 5.

Таблица 3. Результаты расчетов максимальных значений интенсивности напряжений, возникающих в мостике агломерата при ударе о стенку гранулятора по нормали к поверхности стенки.

Таблица 4. Результаты расчетов максимальных значений интенсивности напряжений, возникающих в мостике агломерата при ударе о стенку гранулятора под углом [math] 30^o [/math] к нормали поверхности стенки.

Таблица 5. Результаты расчетов максимальных значений интенсивности напряжений, возникающих в мостике агломерата при ударе о стенку гранулятора под углом [math] 60^o [/math] к нормали поверхности стенки.

Результаты

• Создание конечно-элементных моделей агломератов. Созданные конечно-элементные модели агломератов, будут использованы для дальнейших расчетов напряжений, возникающих в мостике агломерата, под действием нагрузок, выходящих за рамки данного исследования. Модели удара агломератов о стенку гранулятора, будут использованы для расчета напряжений в мостике при ударах под углами от [math] 30^o [/math] до [math] 90^o [/math] относительно нормали к поверхности стенки гранулятора.

• Расчет напряжений, возникающих в мостике агломерата при статической нагрузке. Для расчета таких напряжений, был изучен программный комплекс Abaqus, построены конечно-элементные модели агломератов с различными диаметрами мостиков и сформулирована постановка задачи, при решении которой, получена зависимость максимальных значений напряжений в мостике от диаметра мостика, результаты занесены в табл. 1.

• Аналитический анализ напряжений, возникающих в балке Тимошенко. Для такого анализа, было выведено общее решение, подставлены значения параметров, описывающих мостик агломерата и получены решения для различных диаметров балки. Проведено сравнение результатов аналитического анализа и конечно-элементного моделирования (график 1).

• Расчет напряжений, возникающих в мостике агломерата при ударе о стенку гранулятора. Для данного расчета построены конечно-элементные модели ударов агломерата под углами [math] 0^o [/math], [math] 30^o [/math] и [math] 60^o [/math]. Сформулирована постановка задачи, при решении которой, получена зависимость максимальных значений напряжений в мостике от скорости удара и угла падения агломерата, результаты представлены в таблицах 3, 4 и 5.

Полученные результаты имеют важную роль для дальнейшего изучения процесса окатывания и агломерирования и будут переданы в институт твердых частиц (SPE) гамбургского технического университета (TUHH), для моделирования процесса гранулирования и разработки гранулирующих устройств.