КП: Динамика движения кривошипно-шатунного механизма в двигателе внутреннего сгорания
Курсовой проект по Теоретической механике
Исполнитель: Федоренко Максим
Группа: 08 (23604/1)
Семестр: весна 2014
Аннотация проекта[править]
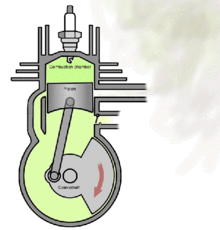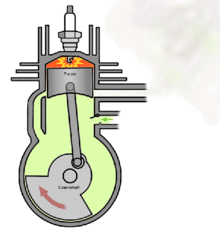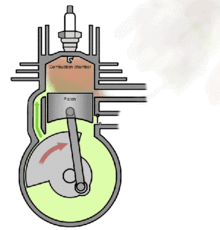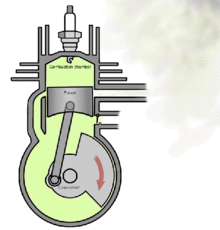
Проект направлен на изучение динамики движения кривошипно-шатунного механизма в двигателе внутреннего сгорания.
Кривошипно-шатунный механизм (КШМ) предназначен для преобразования возвратно-поступательного движения поршня во вращательное движение коленчатого вала. Исследование законов движения КШМ дает возможность получить расчетные формулы для определения величины и характера изменения сил, действующих в основных деталях двигателя при его работе.
Постановка задачи[править]
Изучить характер движения и определить момент инерции шатуна.
Найти зависимость величин сил, действующих на поршень от угла поворота кривошипа.
— длина шатуна (расстояние между осями поршневой и кривошипной головок шатуна)
— радиус кривошипа (расстояние между осями коренной и шатунной шеек кривошипа)
— масса шатуна
Общие сведения по теме[править]
На детали кривошипно-шатунного механизма действуют силы: давления газов, инерции и трения. Особый интерес представляют первые две, имеющие относительно большие и переменные значения и вызывающие деформации, напряжения и колебания, при которых получается динамическое усиление. Шатун совершает плоско-параллельное движение в плоскости перпендикулярной оси коленчатого вала. Силы инерции, действующие на него, при расчете деформаций и прочности должны рассматриваться, исходя из распределения массы по длине. При оценке внешнего действия сил инерции, т.е. действия их в узлах сочленения с поршневым пальцем и шатунной шейкой, производят приведение массы, заменяя сложное распределение ее по длине шатуна конечным числом соответствующих сосредоточенных масс, расположенных на недеформируемом стержне.
Масса шатуна может быть заменена двумя массами, сосредоточенными на осях поршневого пальца , шатунной шейки кривошипа . Такая замена будет эквивалентной при соблюдения следующих условий:
а) сумма всех масс должна быть равна массе шатуна;
б) центр тяжести всех масс должен совпадать с центром тяжести шатуна.
Решение[править]
1.Определение момента инерции шатуна
Приведем массу шатуна к виду:
Центр тяжести всех масс должен совпадать с центром тяжести шатуна ( , где – координаты -ой массы в выбранной системе координат), т.е
или
,
где расстояние от центра масс шатуна до оси поршневого пальца (если начало координат выбрать в центре масс шатуна, а одна из осей совпадает с осью шатуна);
Сумма моментов инерции всех масс относительно оси, проходящей через центр тяжести шатуна, должна быть равна моменту инерции шатуна относительно той же оси
Выразим и :
Тогда момент инерции шатуна выражается как:
(1)
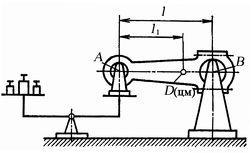
Для определения момента инерции шатуна необходимо знать и , а также положения его центра тяжести (центра масс). Эти величины определяются взвешиванием на рычажных весах. Высоты опор подбирают такими, чтобы при взвешивании ось шатуна была горизонтальной. Расстояние между опорами A и B должно быть равно длине шатуна как показано на рисунке справа. Из условия равновесия:
находим
Подставив полученное значение в формулу (1) получим, что
2.Зависимость величин сил, действующих на поршень от угла поворота коленчатого вала
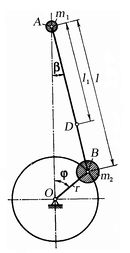
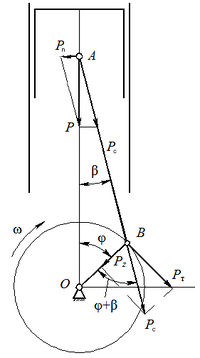
Сила , действующая на поршень может быть разложена на составляющие: , направленная вдоль оси шатуна, и - перпендикулярно (нормально) оси цилиндра. Они могут быть выражены через - угол поворота шатуна относительно центральной оси как:
Найдем зависимость угла поворота шатуна от угла поворота кривошипа . Для этого запишем теорему синусов для треугольника AOB:
– безразмерный параметр КШМ (отношение радиуса кривошипа к длине шатуна)
Значение этого параметра для автомобильных и тракторных двигателей находится в пределах 1/3... 1/4, (т. е. 0,31...0,24). Для решения нашей задачи возьмем и найдем все значения угла .
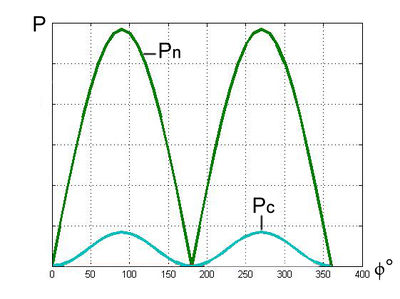
Построим график зависимости и от угла поворота коленчатого вала