Исследование свойств солитона в нелинейном одномерном кристалле

БАКАЛАВРСКАЯ РАБОТА
Автор работы: Александров Сергей
Научный руководитель: Д.В. Цветков

Введение

До середины 1970-х годов для описания физических явлений обычно использовались линейные или <<почти>> линейные модели, что позволяло воспользоваться удобным, но часто нереалистичным свойством таких систем: характеризующаяся замысловатыми причинно-следственными связями система рассматривалась как совокупность нескольких более простых подсистем, влияние которых на совокупную динамику можно было исследовать отдельно. Однако, использование линейной модели вместо нелинейной приводит к потере важных качественных характеристик исследуемого явления.
Известно, что в случае рассмотрения нелинейных систем целое есть нечто большее, нежели простая совокупность его частей и проявляется в образовании новых структур, которые оказываются пространственно или временно когерентными . Одной из таких структур является солитон.
Около 1834 года были замечены уединенные волны и объединены под общим словом солитон. Эту область науки исследовали многие ученые, такие как Скотт Рассел, Энрико Ферми, Мэри Цингоу и другие, но по сей день эта отрасль остается актуальной для экспериментов и теоретических расчетов.
Изучение солитонов в одномерном нелинейном кристалле может пригодиться в механике, морском деле и при использовании лазеров: могут быть использованы для расчета движения барж и лодок в узком канале и для расчета мощности лазера.
Для изучения этой области применяются технологии компьютерного моделирования и теоретические расчеты. Проведение реальных экспериментов требует сложного оборудования. Поэтому наиболее подходящим методом для исследования солитонов является их представление в 1D, 2D и 3D моделях, а так же теоретическое решение некоторых конкретных случаев.
Развитие компьютерных технологий в наше время позволяет достаточно точно прослеживать зависимость характеристик солитона от текущих параметров системы. Изучая нелинейный кристалл, появляется возможность описать реально происходящие процессы, которые нас окружают, что способствует повышенной точности и универсальности решения.
Конкретно в данной работе рассматривается солитон в одномерном нелинейном кристалле с целью предугадывать его поведение в различных системах.

Постановка задачи

Одномерный кристалл

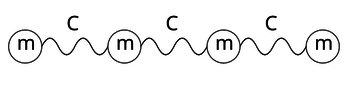
В данной работе рассматривается одномерный нелинейный кристалл, который представляет собой цепочку взаимодействующих частиц, где [math]С[/math] -- жесткость пружин, [math]m[/math] -- масса частиц.

Основные уравнения

В данной работе вместо линейного уравнения динамики цепочки будет использоваться нелинейное:
[math]\ddot{u}_i = \omega ^2 \, (u_{i+1}-u_i) + \alpha ^2 \, (u_{i-1}-u_i)[/math]
где [math]\omega[/math] -- частота колебаний, [math]\alpha[/math] -- коэффициент нелинейности, [math]u_{i}[/math] -- смещение [math]i[/math]-ой частицы относительно положения равновесия.
Нетрудно убедиться, что после несложных математических преобразований уравнение можно записать в виде:
[math]\ddot{u}_i = (u_{i+1} - 2 u_i + u_{i-1}) (\omega ^2 + \alpha^2 (u_{i+1} + u_{i-1}))[/math]

Начальные и граничные условия

На рисунке большими серыми стрелками показаны интересующие нас два максимума, а в серой прямоугольной области - два солитона.

Для задания скорости частиц берется уравнение бегущей волны (хотим получить бегущую в одну сторону волну):
[math]\dot{u} = A \sin(k x - w t)[/math]
где [math]{k}[/math] -- волновой коэффициент, [math]{A}[/math] -- амплитуда колебаний, [math]{w}[/math] -- масштаб времени.
Далее необходимо получить уравнение для перемещений, поэтому берем интеграл по [math]{t}[/math] от уравнения выше и получаем:
[math]u = - \frac{1}{w} A \cos(k x - w t).[/math]
Получились два уравнения: скорости и перемещения. Найдем начальные условия нашей системе положив [math]{t = 0}[/math]:
[math]u|_{t=0} = - \frac{1}{w} A \cos(k x),[/math]
[math]\dot{u}|_{t=0} = A \sin(k x).[/math]
Также, важным начальным условием является большое количество частиц в одномерном кристалле, то есть [math]{N \gt \gt 1}[/math].

Граничные условия у данной системы периодические:
[math]u_k = u_{k+n}.[/math]

Численное решение

Окно программы на JS

При вычислении скорости и перемещений частиц кристалла были использованы следующие уравнения:
Ускорение:
[math]\ddot{u}_i = (u_{i+1} - 2 u_i + u_{i-1}) (\omega ^2 + \alpha^2 (u_{i+1} + u_{i-1})),[/math]
Скорость:
[math]\dot{u}_i(t + \Delta t) = \dot{u}_i(t) + \ddot{u}_i \Delta t,[/math]
Перемещение:
[math]u_i(t + \Delta t) = u_i(t) + \dot{u}_{i}(t + \Delta t)\Delta t.[/math]

Результаты

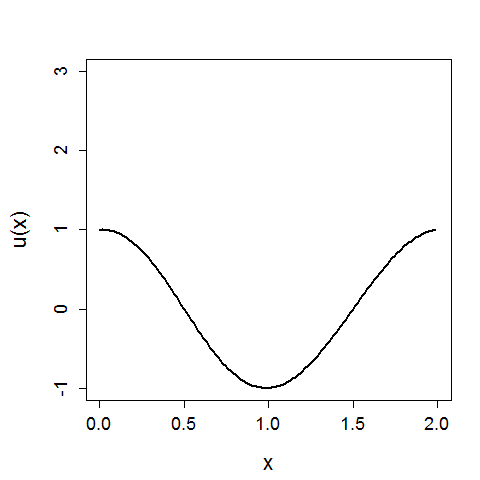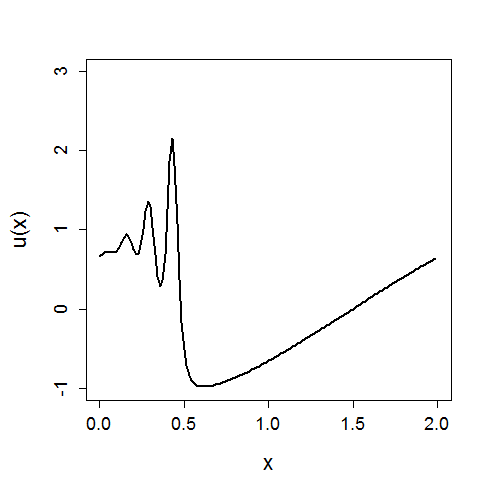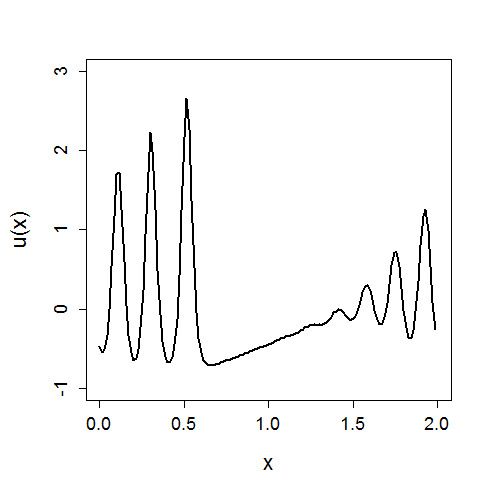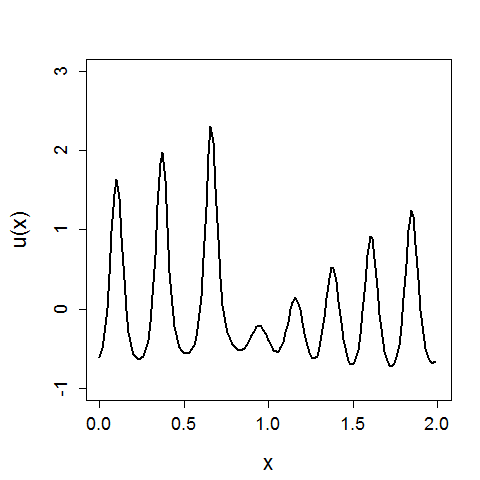
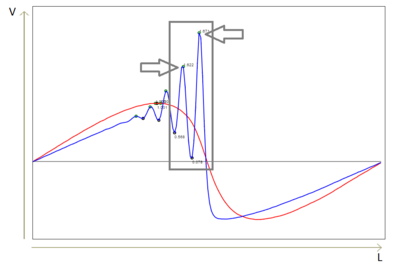
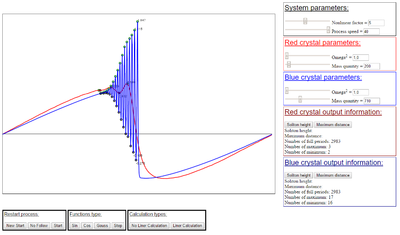
Для выявление зависимостей характеристик солитона от параметров система была написана программа на языке JavaScript, позволяющая наглядно наблюдать образование солитона и сравнивать два одномерных кристалла, варьируя их параметры.
Для установления зависимостей параметров системы от нелинейного коэффициента [math]\alpha[/math] был проведен следующий эксперимент: смоделирован одномерный нелинейный кристалл при различных [math]\alpha[/math]. Параметры системы: частота [math]\omega^2 = 1[/math], количество частиц [math]N = 500[/math]. Исследуемые параметры:
[math]Т_{раз}[/math] -- время за которое на волне образуются солитоны,
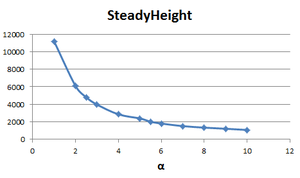
[math]Т_{уст}[/math] -- время за которое высота солитона выходит на постоянный уровень,
[math]h_{сол}[/math] -- высота солитона в отношении к начальной амплитуде колебаний волны,
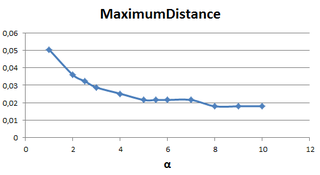
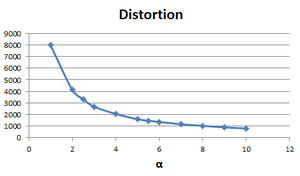
[math]s_{экс}[/math] -- расстояние между максимумами первых двух солитонов в отношении к длине кристалла.

Результаты показаны в виде графиков ниже:

Зависимость [math]s_{экс}[/math] от [math]\alpha[/math]

Зависимость [math]Т_{уст}[/math] от [math]\alpha[/math].

Зависимость [math]Т_{раз}[/math] от [math]\alpha[/math].

Выводы

До 1965 года полагали, что динамика нелинейных дифференциальных уравнений в частных производных настолько сложна, что практически не представляется возможным получить их аналитические решения. К настоящему моменту известно несколько дюжин подобных систем (некоторые из которых связаны с практическими приложениями), для которых точные решения были получены с использованием методов, основанных на понимании солитона как новой динамической сущности, образующейся из соответствующего дифференциального уравнения. Этот результат, важный сам по себе, расширяет область применения теории возмущений, поскольку позволяет исследователю выбрать в качестве оценки нулевого порядка полностью нелинейную функцию (скажем, выражение для N -- солитона).
Результатом данной работы стало определение зависимостей характеристик солитона от параметров системы, а конкретно:

• Наблюдается степенная зависимость между коэффициентом нелинейности [math]\alpha[/math] и расстоянием между максимумами первых двух солитонов [math]s_{экс}[/math].
• Наблюдается гиперболическая зависимость между коэффициентом нелинейности [math]\alpha[/math] и временем образования солитона [math]Т_{раз}[/math].
• Наблюдается гиперболическая зависимость между коэффициентом нелинейности [math]\alpha[/math] и временем установления высоты солитона [math]Т_{уст}[/math].
• Наблюдается степенная зависимость между количеством частиц [math]N[/math] и расстоянием между максимумами первых двух солитонов [math]s_{экс}[/math].
• Наблюдается линейная зависимость между количеством частиц [math]N[/math] и временем образования солитона [math]T_{рас}[/math].
• Наблюдается линейная зависимость между количеством частиц [math]N[/math] и временем установления высоты солитона [math]T_{уст}[/math].

Таким образом, были выявлены интересующие нас зависимости, которое позволяют прогнозировать поведение солитона в зависимости от условий системы.
Дальнейшей работой в этой области будет усовершенстование программы расчета, а именно рассмотрение влияния различных начальных условий на солитоны и проведение реального эксперимента для сравнения с аналитическим решением.

Список литературы

• Э. Скотт. Нелинейная наука. Развитие и рождение когерентных структур.
• J. Scott Russell. Report on Waves. 14th meeting of the British Association for the Advancement of Science (BAAS), 1844.
• J Boussinesq. Theorie des ondes et des remous qui se propagent le long d’un canal rectangulairc horizontal, en communiquant au liquid contenu dans ce canal des vitesses sensiblement pareilles de la surface au fond.
• D. J. Korteweg and H. De Vries. On the change of form of long waves advancing in rectangular canal, and on new type of long stationary waves.
• R. Pego. Origin of the KdV equation.
• J Boussinesq. Theorie des ondes et des remous qui se propagent le long d’un canal rectangulairc horizontal, en communiquant au liquid contenu dans ce canal des vitesses sensiblement pareilles de la surface au fond.
• Fermi E., Pasta J.R., Ulam S. Studies of nonlinear problems. Report LA-1940. Los Alamos: Los Alamos Scientific Laboratory, 1955.
• Улам С. Приключения математика. Москва–Ижевск: Регулярная и хаотическая динамика,2002. 272 с.
• Porter M.A., Zabusky N.J., Hu B., Campbell D.K. Fermi,Pasta, Ulam and the Birth of Experimental Mathematics // American Scientist. 2009. V. 97. № 3. P. 214–221. doi: 10.1511/2009.78.214
• Dauxois T., Peyrard M., Ruffo S. The Fermi-Pasta-Ulam “numerical experiment” history and pedago.
• Genta T., Giorgilli A., Paleari S., Penati T. Packets of resonant models in Fermi-Pasta-Ulam system // Phys. Lett. A. 2012, V. 376. P. 2038–2044.
• Н. А. Кудряшов. Дифференциальные уравнения и динамические системы.
• А. М. Кривцов. Курс лекций по динамике одномерного гармонического кристалла.