Исследование отрицательного теплового расширения цепочки с продольной и изгибной жесткостью

БАКАЛАВРСКАЯ РАБОТА
Автор работы: Марков Николай
Научный руководитель: В.А. Кузькин

Введение

Большинство известных веществ имеют положительный коэффициент теплового расширения. Это означает, что при увеличении температуры вещество расширяется, увеличивая занимаемый объем. Но существуют вещества, обладающие отрицательным коэффициентом теплового расширения. Хорошо известный пример такого вещества - лед. Но помимо льда отрицательным коэффициентом теплового расширения обладают и многие другие вещества, которые активно используются в науке и технике. Поэтому исследование физических процессов, лежащих в основе отрицательного теплового расширения, является актуальной проблемой. Основной причиной теплового расширения веществ являются продольные и поперечные колебания частиц, поэтому аналитическое предсказание зависимости коэффициента теплового расширения от микроскопических свойств вещества является довольно трудной задачей, решение которой предполагает использование методов статистической физики. Минус такого подхода в том, что для получения результата необходимо произвести сложные математические расчеты, такие как, например, вычисление интеграла в N - мерном фазовом пространстве. Использование метода динамики частиц для решения данной задачи позволяет получить количественные и качественные результаты, избегая сложных вычислений. В работе <<Nonlinear positive/negative thermal expansion and equations of state of a chain with longitudinal and transverse vibrations>> было проведено исследование теплового расширения цепочки с продольными и поперечными колебаниями частиц, обладающей только продольной жесткостью. В данной работе было показано, что параметр Грюнайзена меняется от [math]-\infty[/math] до +[math] \infty [/math] при изменении деформации цепочки от нуля до критического значения. Также аналитически и численно было показано, что зависимость температурного давления от температурной энергии нелинейна при малых деформациях цепочки, а при некоторых значениях деформации еще и не монотонна. Из всего вышеперечисленного делается предположение, что у реально существующих веществ зависимость температурного давления от температурной энергии при давлениях, близких к критическим, будет не линейной, что подтверждается экспериментальными данными. В связи с этим необходимо исследовать модель цепочки, более приближенную к реальной. Для этого предлагается поэтапно усложнять модель, добавляя в нее новые параметры.

В данной работе исследуется тепловое расширение двумерной цепочки с продольной и изгибной жесткостью, частицы которой совершают продольные и поперечные колебания. Целью данной работы является исследование свойств данной цепочки при растяжении, а так же сжатии при деформациях, меньших или равных критической.

Модель цепочки

В данной работе моделирование цепочки проводится методом динамики частиц.В начальный момент времени частицы цепочки находятся на одинаковом расстоянии [math] a [/math] друг от друга и обладают произвольными скоростями, равномерно распределенными в круге. Частицы цепочки обладают продольной и поперечной компонентой скорости, что приводит к наличию отрицательного теплового расширения. Потенциал взаимодействия между частицами цепочки

[math] \Pi = \Pi_{lj} + \Pi_s [/math]

Потенциал [math] \Pi_{lj} [/math] является потенциалом Леннарда-Джонса и имеет вид

[math] \Pi_{lj} = D \biggl[ \left (\frac{a_0}{r}\right)^{12} - 2\left(\frac{a_0}{r}\right)^{6}\biggr] [/math]

Потенциал [math] \Pi_{} [/math] является потенциалом угловой пружинки и имеет вид

[math] \Pi_s = \frac{c_s (\varphi-\pi)^2}{2} [/math]

В модели используются периодические граничные условия и учитывается взаимодействие только между ближайшими соседями. Интегрирование уравнения движения используется модифицированный алгоритм Верле.

Параметры системы

На каждую рассматриваемую частицу действует сила

[math] F = F_1 + F_{-1} [/math]

где [math] F_1 [/math] и [math] F_{-1} [/math] - силы, действующие на частицу со стороны ее соседей. Макроскопическими параметрами являются тепловое давление [math] p_T [/math] и тепловая энергия [math] E_T [/math]. Тепловое давление определяется формулой

[math] p_T = p - p_0, \,\,\, p = - \langle F_1 \rangle \cdot e_1 [/math]

Здесь [math] \langle F_1 \rangle[/math] - средняя сила, действующая на рассматриваемую частицу в направлении вектора [math] e_1 [/math], где [math] e_1 [/math] - вектор, коллинеарный цепочке в начальный момент времени. [math] p_0[/math] - холодное давление, характеризующее давление в цепочке в начальный момент времени. Тепловая энергия определяется соотношением

[math] E_T = K_T + U_T, \,\,\, K_T = \frac{m}{2} \langle \tilde v^2\rangle, \,\,\, U_T = \langle\text П\rangle - \text П_0 [/math]

здесь [math] \langle\text П\rangle [/math] - среднее значение потенциала взаимодействия в актуальной конфигурации, [math] \text П_0 [/math] - значение потенциала взаимодействия, [math] \langle \tilde v\rangle [/math] - среднее значение модуля скорости. Значения в данной модели для каждой точки на графике усредняются по разному, в зависимости от числа частиц в цепочке. При [math] n = 100 [/math] значения усредняются 60 раз по начальным условиям и [math] 3 \cdot 10^5 [/math] раз по временному шагу. При [math] n = 1000 [/math] значения усредняются 20 раз по начальным условиям и [math] 3 \cdot 10^5 [/math] раз по временному шагу. При [math] n = 10000 [/math] значения усредняются только [math] 3 \cdot 10^5 [/math] раз по временному шагу. Обезразмеривание [math] E_T [/math] происходит путем деления тепловой энергии на энергию взаимодействия [math] D [/math], а [math] p_T [/math] путем деления теплового давления на [math] \displaystyle \frac{D}{a_0} [/math].

Растяжение цепочки

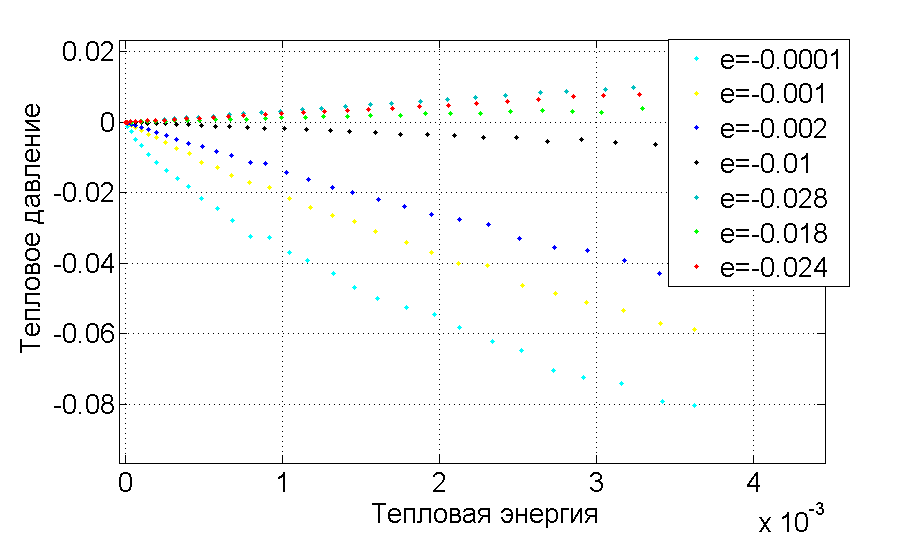
Посмотрим, как влияет растяжение цепочки на зависимость [math]p_T(E_T)[/math]. На рисунке, представленном ниже, видно, что при растяжении зависимость тепловой энергии [math]p_T[/math] от теплового давления [math]E_T[/math] линейна. Это означает, что в данном случае для получения зависимости [math]p_T(E_T)[/math] можно воспользоваться уравнением состояния Ми-Грюнайзена

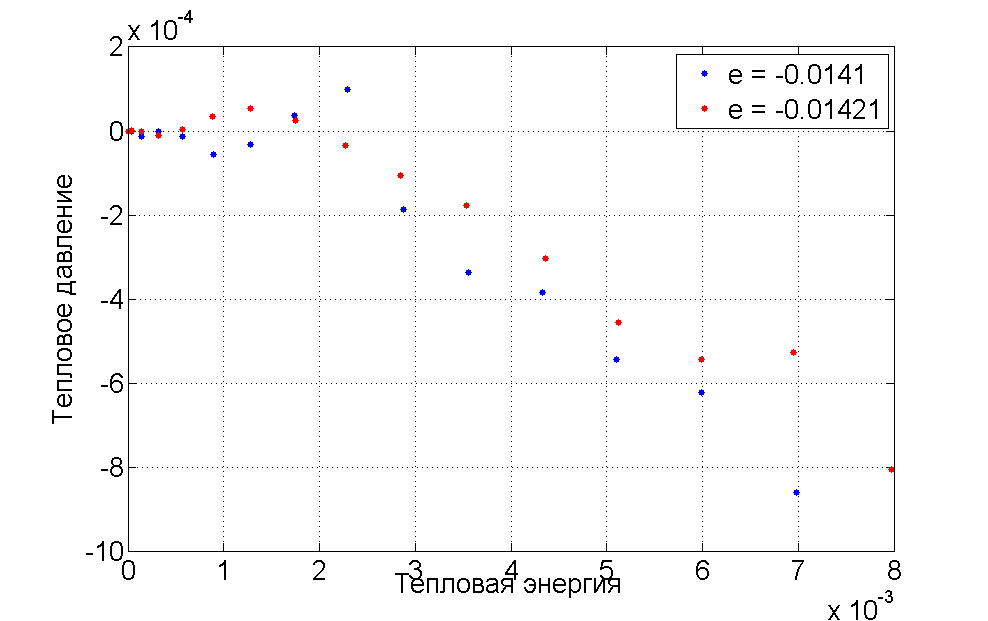
Также можно наблюдать, что при определенных значениях деформации цепочка имеет как положительный коэффициент теплового расширения, так и отрицательный. Здесь стоит отметить, что линейность зависимости [math]p_T[/math] от [math]E_T[/math] показана только в случаях, когда деформация цепочки не совпадает с деформацией [math]\varepsilon_*[/math], при которой реализуется случай нулевого теплового расширения. Рассмотрим более подробно поведение цепочки при растяжении от 1\% до 1.8\%. При значениях деформации [math]\varepsilon \in [-0.01, -0.018][/math] наблюдается переход от отрицательного теплового расширения к положительному, а так же при одном из этих значений реализуется ситуация нулевого теплового расширения. Так как для данной модели из-за нецентральности сил сложно составить аналитическое решение, для нахождения [math]\varepsilon_*[/math] необходимо провести серию численных экспериментов при растяжении цепочки от [math]1\%[/math] до [math]1.8\%[/math]. В результате численного моделирования было получено, что [math]\varepsilon_* \sim -0.0141[/math], что соответствует растяжению цепочки на [math]1.41\%[/math].

Сжатие цепочки

В работе ставится задача исследовать свойства системы при деформациях, близких к критической

[math] \varepsilon_{cr} = \frac{4 \pi^2 c_s n}{(n-1)^3 c_l} [/math]

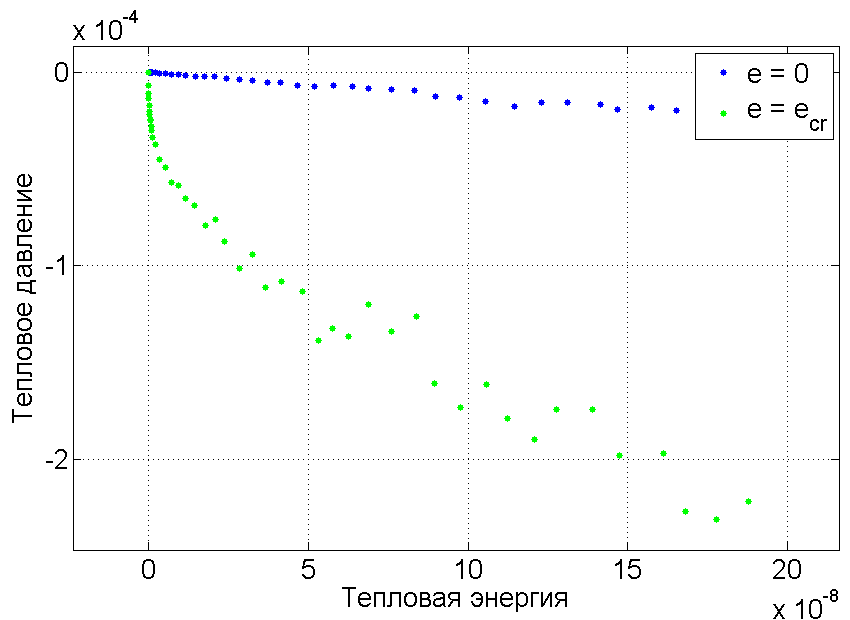
Рассматриваемая цепочка, состоящая из 100 частиц теряет устойчивость при [math]m = 2[/math] со значением критической деформации [math]\varepsilon_{cr} = 5.65 \cdot 10^{-5}[/math].

Рассмотрим график зависимости [math]p_T(E_T)[/math] в случае критического сжатия и сравним с графиком, полученным для недеформированной цепочки. На рисунке, представленном ниже, видно, что в случае критической деформации зависимость [math]p_T(E_T)[/math] нелинейна при малых значениях [math]E_T[/math], тогда как в случае нулевой деформации данная зависимость является линейной. Таким образом, в случае критического сжатия цепочки нельзя пользоваться уравнением состояния Ми-Грюнайзена для описания зависимости [math]p_T(E_T)[/math] даже при малых энергиях, так как данное уравнение предполагает линейную зависимость теплового давления от тепловой энергии. Таким образом можно сделать вывод, что для цепочки, обладающей продольной и изгибной жесткостью, параметр Грюнайзена [math]\text Г = -\infty[/math] в случае критической деформации, а не в случае нулевой деформации, как было для цепочки, обладающей только продольной жесткостью. Данный вывод хорошо согласуется с результатом анализа влияния изгибной жесткости на зависимость [math]p_T(E_T)[/math].

Выводы

В данной работе численно исследовано тепловое расширение цепочки, обладающей продольной и изгибной жесткостью. Для численного моделирования методом динамики частиц написана программа на языке $C++$. Программа имеет все модули для того, чтобы обеспечить возможность добавления в модель новых параметров, не прибегая к сложным функциям языка. В процессе исследования было проанализировано несколько различных конфигураций цепочки, отличающихся друг от друга как видом деформации, так и значениями тепловой энергии. В результате анализа полученных данных можно можно сделать следующие выводы:

• Зависимость [math]p_T(E_T)[/math] при растяжении цепочки линейна при значениях деформации [math]\varepsilon \neq \varepsilon_*[/math].

• Характер теплового расширения меняется при [math]\varepsilon \sim \varepsilon_* \sim -0.0141[/math]. При данном значении деформации реализуется ситуация нулевого теплового расширения.

• При [math]\varepsilon \sim \varepsilon_* \sim -0.0141[/math] зависимость [math]p_T(E_T)[/math] не только не линейна, но и не монотонна.

• При деформации [math]0 \lt \varepsilon \leqslant \varepsilon_{cr}[/math], то есть при сжатии цепочки, наблюдается изменение формы зависимости [math]p_T(E_T)[/math] с линейной на сильно нелинейную при малых значениях [math]E_T[/math]. Это приводит к тому, что [math]\text Г = - \infty[/math] для случая критического сжатия цепочки.

• Предположение о том, что при критическом сжатии цепочки зависимость [math]p_T(E_T)[/math] сильно нелинейна, подтвердилось. Таким образом, можно ожидать, что данный эффект можно также наблюдать в графеновых нанотрубках или в графеновых листах при давлении, близкому к критическому.

• Все свойства, которыми обладала цепочка без изгибной жесткости, наблюдаются и в данной модели. Это означает, что наличие изгибной жесткости приводит к изменению количественных параметров системы, например таких как [math]\varepsilon_* $ и $\varepsilon_{cr}[/math], но при этом характер зависимости [math]p_T(E_T)[/math] существенно не меняется.

Список использованной литературы

• K. Rottiger, A.Endriss,Jorg Ihringer, S.Doyle, W.F.Kuhs. <<Lattice constants and thermal expansion of [math] H_2O [/math] and [math] D_2O [/math] Ice Ih between 10 and 265 K>>, Addendum, Acta Crystallographica
• Joseph N. Grima, Victor Zammit and Ruben Gatt. <<Negative Thermal Expansion>>, Msida MSD 06, Malta.
• John S. O. Evans. <<Negative thermal expansion materials>>, Journal of the Chemical Society, Dalton Transactions, Issue 19, 1999
• P.R.L. Welche, V. Heine M.T. Dove. <<Negative thermal expansion in beta-quartz>>, Phys Chem Minerals (1998)
• Kuzkin V.A., Krivtsov A.M. <<Nonlinear positive/negative thermal expansion and equations of state of a chain with longitudinal and transverse vibrations>>, 2015.
• M.Born, Th. von Karman. <<Uber Schwingungen in Raumgittern>>, Physikzeitschrifft, 13:297-309,1912
• M.P. Allen, D.J. Tildesley. <<Computer Simulation of Liquids>>. Oxford Science Publications, Clarendon Press, Oxford, 1987
• А.М. Кривцов. <<Деформирование и разрушение твердых тел с микроструктурой>>. М.: Физматлит, 2007. 304 с.
• Verlet L.(1967). <<Computer 'experiments' on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules>>. Phys. Rev. 159: 98–103. doi:10.1103/physrev.159.98.
• Andrew Noske <<Efficient Algorithms for Molecular Dynamics Simulations and Other Dynamic Spatial Join Queries>>
• L. Verlet, Phys. Rev., 159 (1967).
• Vitaly A. Kuzkin, Jizeng Wang <<Infuence of thermal motion on bending stiffness of nanoscale rod-like structures>>, March 18, 2008