Исследование зависимости коэффициента сдвига от параметров сечения стержня.
МАГИСТЕРСКАЯ РАБОТА
Автор работы: Прокопенко Анастасия
Научный руководитель: д.ф.-м.н. Иванова Елена Александровна
Содержание
- 1 Введение
- 2 Методы определения упругих модулей
- 3 Постановка задачи для определения коэффициента сдвига
- 4 Сравнение решений задачи для балки Бернулли-Эйлера и Тимошенко
- 5 Влияние отверстий в сечении на коэффициент сдвига ([math]J_x = J_y[/math])
- 6 Влияние отверстий в сечении на коэффициент сдвига ([math]J_x \neq J_y[/math])
- 7 Выводы
- 8 Список литературы
Введение[править]
Модули жёсткости на растяжение, изгиб и кручение хорошо известны и приведены во всех справочниках. Интерес представляет модуль жёсткости на поперечный сдвиг. Существует формула для коэффициента сдвига . Зависимость от и вопроса не вызывает, интерес представляет значение и его нахождение. Существует два метода вывода основных уравнений тонких стержней: асимптотический и прямой. Асимптотический метод основан на уравнениях трехмерной теории и ряде априорных предположений относительно внутренней структуры стержня и характера поведения решения. Если коэффициент выводится асимптотическим методом, то он получается равным единице. Прямой метод основан на непосредственном использовании фундаментальных законов механики. Этот метод имеет более широкую область применимости, поскольку при выводе основных уравнений не делается никаких предположений о характере поведения решения, а все особенности внутренней структуры стержня содержатся в тензорах жесткости. При прямом методе коэффициент может принимать различные значения.
Были предложены различные искусственные приемы отыскания корректирующего коэффициента в уточненных теориях, основанных на сдвиговой модели Тимошенко. Все эти приемы являются приближенными. При построении уточненных уравнений, как математических аппроксимаций краевой задачи динамической теории упругости, не требуется введения каких–либо искусственных величин. Поэтому из сравнения математических аппроксимаций с соответствующими уточненными теориями, содержащими искусственные величины, можно найти формулы для корректирующих коэффициентов, иногда в явном виде.
В работах Ю. М. Гаврилива (1960-1968) изучается влияние деформаций сдвига на прогибы балок при статических нагрузках. Это влияние можно характеризовать коэффициентом сдвига, который зависит от формы поперечного сечения, коэффициента Пуассона и вида нагружения (сюда можно отнести и граничные условия). Для стержня прямоугольного поперечного сечения конечной длины, нагруженной сосредоточенной силой, следует формула для коэффициента сдвига: Здесь - число Пуассона. Д. Гросс (1969) построил точное решение в рамках плоского напряженного состояния для балки–стенки со свободно поворачивающимися концами. С помощью этого решения вычислен коэффициент сдвига по следующей формуле:
В следующей работе Д. Гросс (1971) на основе уравнений плоского напряженного состояния построил точные решения для гармонических колебаний бесконечной ортотропной балки-стенки, характеризуемой продольным , поперечным и сдвиговым модулями упругости. В случае несимметричных относительно срединной поверхности колебаний выведено и исследуется дисперсионной уравнение в предельных случая длинных волн и коротких (волны Релея). Показано, что дисперсия волн сильно зависит от отношения . Коэффициент сдвига определяется по формуле (при больших длинах волн):
В 1951 году в теории оболочек для коэффициента сдвига было получено значение: которое впервые было предложено Р. Миндлиным и мало отличается от известного значения Э. Рейсснера:
Также в теории оболочек П.А.Жилиным было получено следующее значение для коэффициента сдвига:
Методы определения упругих модулей[править]
Существует два метода определения упругих модулей стержней. Оба эти метода основаны на сравнении результатов решения трехмерных задач с результатами решения соответствующих задач теории стержней. Первый метод основан на использовании динамических тестовых задач и заключается в сравнении собственных частот. Второй метод основан на решении статических задач. При этом сравниваются величины, характеризующие напряженно-деформируемое состояние. Далее будем сравнивать кинематические характеристики. В результате решения трехмерной задачи получаем распределение перемещений по сечению стержня. Существуют различные подходы к определению соотношений между перемещениями трехмерного тела и перемещением и поворотом сечения стержня. Далее будет использоваться подход, согласно которому считается, что количество движения и кинетический момент стержня и трехмерного тела (прообраза) совпадают между собой. Проинтегрировав данное соотношение по времени, придем к следующим уравнениям: где - объемная плотность массы материала стержня, - вектор смещений точек трехмерной среды, - вектор положения точек поперечного сечения, - площадь поперечного сечения.
Постановка задачи для определения коэффициента сдвига[править]
Рассматривается задача изгиба стерженя длинной (см. Рис. 1). Один конец жестко закреплен, на втором конце действует поперечная сила . Решение будем искать в виде: . Имеем: Здесь - перемещение стержня со свободным концом, - угол поворота сечения стержня со свободным концом, - модуль жесткости на поперечный сдвиг, - модуль жесткости на изгиб.
Решение содержит два неизвестных модуля упругости. При вычислении может возникнуть проблема. В формуле для перемещения слагаемое содержащее жесткость на сдвиг является поправочным. Поэтому для его определения задача должна быть решена с высокой точность. Формула для упределения упругих модулей содержит интегралы от перемещений, которые находятся в результате решения трехмерной задачи. В конечно-элементном пакете мы находим набор дискретных величин. Значит нужно вычислять римановы суммы, а это вносит погрешность. Модуль жесткости на кручение также вычисляется с погрешностью.
При решении этой задачи нужно раскрыть векторное произведение в правой части формулы для определения модуля упругости. Из-за большого количества узлов погрешность будет большой. Чтобы избежать эту проблему нужно решить две задачи: изгиб стержня со свободным концом и с заделкой, как показано на Рис 1.
Угол поворота сечения и перемещение для стержня с двумя заделками: где - перемещение стержня с заделкой с двух сторон, - угол закручивания стержня с заделкой с двух сторон.
Переходим к относительной координате сечения, делая замену . Получаем итоговую формулу для модуля жесткости на поперечный сдвиг: Перейдем от найденного модуля жесткости на поперечный сдвиг к коэффициенту сдвига:
Здесь - модуль сдвига, - площадь поперечного сечения.
Сравнение решений задачи для балки Бернулли-Эйлера и Тимошенко[править]
Рассматривается задача, изображенная на Рис. 1, когда один конец жестко закреплен, а второй конец свободный и находится под действием поперечной силы. Полученное решение в пункте "Постановка задачи для определения коэффициента сдвига" - есть решение задачи в случае балки Тимошенко, где .
Для балки Бернулли-Эйлера будем иметь решение:
Вычислим абсолютную погрешность решений как разницу решений:
Рассмотрим случай, когда в сечении прямоугольник со сторонами на . Среднее значение коэффициента сдвига будет равно . Тогда модуль жесткости на поперечный сдвиг будет равен: .
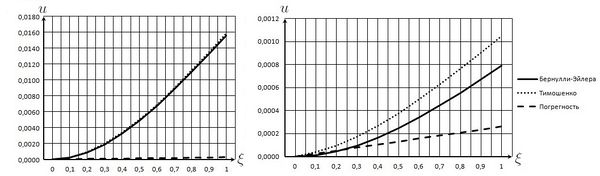
Изобразим на графиках (Рис 2.) для данного случая решения Бернулли-Эйлера и Тимошенко, а также погрешность этих решений , в зависимости от позиции сечения.
При сравнении решений Бернулли-Эйлера и Тимошенко был рассмотрен пример с конкретной формой сечения. Поведение графиков, будет такое же и для других форм сечения.
По этим графикам видно, что в случае тонкого стержня решения Бернулли-Эйлера и Тимошенко практически совпадают и погрешность будет минимальной. Таким образом, сдвиговые эффекты практически не влияют на изгиб тонких стержней. Поэтому при попытке определить коэффициент сдвига путем экспериментов с тонкими стержнями, результаты объективно оказываются недостоверными. С другой стороны, при расчете любых стержней (как толстых, так и тонких) по теории Тимошенко можно использовать значение коэффициента сдвига, найденное путем экспериментов с толстыми стержнями.
Влияние отверстий в сечении на коэффициент сдвига ()[править]
Введём безразмерный параметр , характеризующий геометрическое место отверстий. Этот параметр зависит от расположения и размера отверстий.
Хотим оценить зависимость коэффициента сдвига от для квадратных и круглых форм сечений сплошных и с отверстиями, когда .
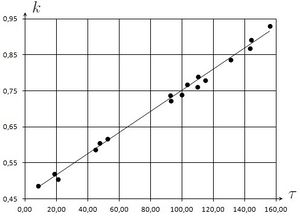
Для графика, изображенного на Рис 3., уравнение аппроксимирующей прямой имеет вид: .
Таким образом, зависимость коэффициента сдвига от коэффициента Пуассона находится в пределах погрешности эксперимента. Тогда зависимость коэффициента сдвига от безразмерного параметра можно записать в виде:
Влияние отверстий в сечении на коэффициент сдвига ()[править]
Видим на Рис 4., что некоторые точки плохо ложатся на прямую. Поэтому формулу, полученную в пункте "Влияние отверстий в сечении на коэффициент сдвига ()" нужно модифицировать.
Итоговая формула для этого случая:
Выводы[править]
Напишем основные результаты полученные в данной работе.
- Была определена зависимость коэффициента сдвига от безразмерного параметра , характеризующий геометрию сечения, когда моменты инерции совпадают, т.е. ().
- Определена зависимость коэффициента сдвига от коэффициента Пуассона.
- Удалось получить формулу для определения зависимости коэффициента сдвига от безразмерных параметров: , и , когда моменты инерции не совпадают, т.е. ().
Список литературы[править]
- В. И. Водопьянов, А. Н. Савкин, О. В. Кондратьев. Курс сопротивления материалов с примера и задачами. Учебное пособие, 2012.
- Э. И. Григолюк, И. Т. Селезов. Механика твердых деформируемых тел. Том 5. Неклассические теории колебаний стержней, пластин и оболочек.
- Mindlin R.D. influence of rotatory inertia and shear on flexural vibrations of isotropic, elastic plates // J. Appl. Mech. 1951. 18. P. 31–38.
- П. А. Жилин. Прикладная механика. Основы теории оболочек. Издательство Политехнического университета, 2006
- П. А. Жилин. Прикладная механика. Теория тонких упругих стержней. Издательство Политехнического университета, 2007
- В. К. Манжосов. Сопротивление материалов. Определение внутренних силовых факторов. - Учебное пособие. Ульяновск, УлГТУ.
- Феодосьев В. И. Сопротивление материалов. — М.: изд-во МГТУ им. Н. Э. Баумана, 1999
- Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. В 10-ти т. Т. VII. Теория упругости: Учеб. пособие. — 4-е изд., испр. и доп. — М.; Наука. Гл. ред. физ.-мат. лит., 1987. — 248 с.
- С. Г. Рабинович. Погрешности измерений. - Л.:Энергия. 1978.
- Erasmo Carrera, Gaetano Giunta, Marco Petrolo. Beam Structures: Classical and Advanced Theories.
- O. A. Bauchau, J. I. Craig. Euler-Bernoulli beam theory. Springer Netherlands, 2009.
- R. K. Bansal. A text book of strength of materials. Laxmi publications (p) ltd. 1996.
- M. Spittel, T. Spittel. Young's modulus of steel. Springer Berlin Heidelberg, 2009.
- David Roylance. Mechanical properties of materials. MIT 2008.