Динамическая потеря устойчивости дискретного стержня при сжатии

БАКАЛАВРСКАЯ РАБОТА

Рис.1 Первая форма потери устойчивости

Рис.2 Вторая форма потери устойчивости

Рис.3 Третья форма потери устойчивости

Автор работы: П. Д. Киселев
Руководитель: зам. зав. кафедры ТМ В. А. Кузькин

Введение

Деформация стержней (колонн, балок) является классической задачей для механики твердых тел. Около пятидесяти последних лет активно изучались упругие системы и связанная с ними динамическая потеря устойчивости, приводящая к разрушениям. Изучение динамических нагрузок является объектом пристального внимания исследователей.

Постановка задачи

Рис.4 Цепочка частиц

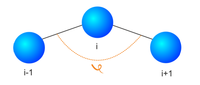
Рассматривается цепочка в двумерном пространстве, состоящая из материальных точек, соединенная линейными и угловыми пружинами (Рис.1)
Уравнение движения: [math] m\bar{a} = \bar{F_c} + \bar{F_s} [/math]
Начальные условия: Частицы находятся на равновесном расстоянии a и обладают случайными начальными скоростями
[math]V_i = V_{rand}[/math] ; [math]x_i = ai[/math]; [math]y_i = 0[/math]
Граничные условия: Левый конец цепочки закреплен, правому задана постоянная скорость.
[math]u_1 = 0[/math]; [math]u_n = -Vt[/math]

В ходе работы решались следующие задачи:
1. Построение модели дискретного стержня и моделирование с разными параметрами: температура, скорость сжатия.
2. Обработка и анализ получившихся зависимостей
3. Сравнение с континуальной постановкой задачи. Задача Хоффа.

Параметры системы

Для проведения моделирование задаются следующие параметры: масса частиц [math] m=1[/math], масштаб силы[math] f=12D/a=1[/math], равновесное расстояние[math] a=1[/math], жесткость угловой пружины[math] c=fa=1[/math], количество частиц в цепочке[math] n=100[/math], скорость длинных волн[math] v_0=√{6fa}=√6[/math], амплитуда начальных случайных скоростей (температура)[math] v_{rand}=5e^{-8} v_0[/math], скорость сжатия цепочки[math] V=1.1e^{-6} v_0[/math].

Случайные начальные скорости определяют температуру системы.

Взаимодействия в системе

В системе имеется два типа взаимодействия:

1. Потенциал Леннарда-Джонса:
[math]П_{LG}=D[( \frac {a_0}{r})^{12}- 2(\frac {a_0}{r})^6 ][/math]
где D - энергия взаимодействия; a0 – начальная длина; r – расстояние между частицами.
Сила взаимодействия, соответствующая потенциалу Леннарда-Джонса, вычисляется по формуле:
[math]F_{LG}=-П'_{LG}=12 \frac {D}{a_0}[( \frac {a_0}{r})^{13}- (\frac {a_0}{r})^7 ][/math]

2. Потенциал угловой пружины:

Рис.5 Угловая пружинка

Частицы соединены угловой пружиной, как показано на Рис.2.
[math]П_s= \frac {c_s(φ-π)^2}{2}[/math]
где Cs – жесткость, φ – угол образованный 2-мя соседними связями.
Силы, соответствующая потенциалу угловой пружины, вычисляются:
[math]F_{i-1}=-\frac {∂П_s}{∂r_{i-1}}[/math]
[math]F_i=-\frac {∂П_s}{∂r_i}[/math]
[math]F_{i+1}=-\frac {∂П_s}{∂r_{i+1}}[/math]

Виды нагружения

Для исследования задач о динамической потери устойчивости стержня имеются следующие варианты нагрузок:

1. Внезапное приложение силы (задача Ишлинского- Лаврентьева)
2. Удар твердого тела о стержень
3. Сжатие с постоянной скоростью (Задача Хоффа)

Задача Хоффа

Рис.6 Стержень с начальной кривизной

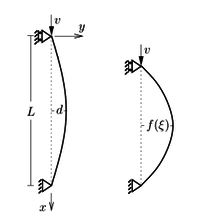
В задаче Хоффа рассматривается стержень с начальной кривизной.
Задается уравнение поперечных колебаний балки:
[math] \frac {∂^2}{∂x^2} (EI[\frac {∂^2 y}{∂x^2}-\frac {∂^2 y_0}{∂x^2}])+P\frac {∂^2 y}{∂x^2}+μA\frac {∂^2 y}{∂t^2}=0 [/math]

[math]\frac {∂^2 y(x=0)}{∂x^2}=\frac {∂^2 y(x=L)}{∂x^2}=0 [/math]
Уравнение для продольной силы:
[math] P= \frac {EA}{L} (2ϑt-\frac {1}{2} ∫_0^L[(\frac {∂y}{∂x} )^2-(\frac {∂y_0}{∂x} )^2 ]dx)[/math]
Начальные и граничные условия:
[math] y|_{x=0}=y|_{x=L}=0 [/math]
[math] \frac{∂^2 y}{∂x^2} |_{x=0}= \frac {∂^2 y}{∂x^2} |_{x=L}=0 [/math]

Данная задача решена в работе [4] и получено следующее решение: зависимость критической силы от скорости сжатия.

[math] \frac {P_*}{P_E} =1+( \frac {3}{4Ω^{1/2}} ln⁡(\frac {2}{πd^2 Ω}) )^{2/3}, Ω=π^8 (\frac {R}{L})^6 (\frac {υ_s}{υ}) [/math]
где d – переменная характеризующая кривизну стержня, Ω – функция скорости.
Это решение мы используем для сравнения с результатами данной работы.
В данной работе моделируется стержень также с постоянной скоростью сжатия, но вместо начальной кривизны, задается начальная случайная скорость для частиц цепочки (начальное отклонение)

Результаты моделирования

Рис.7 Продольная сила в стержне

Рис.8 Продольная сила. Задача Хоффа. Взято со статьи [4]

Важно отметить, что для потери устойчивости в данной работе задается начальная случайная скорость (Vrand) для частиц цепочки. Она определяет температуру системы. А в задаче Хоффа в качестве неидеальности задается параметр d – кривизна.

Продольная сила в стержне

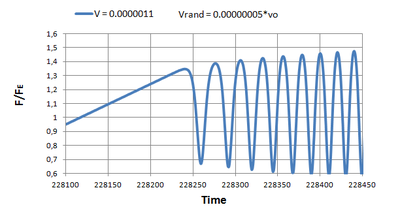
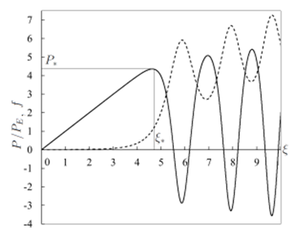
Для определения значения критической силы строится зависимость продольной силы от времени для цепочки (Рис. 7), состоящей из материальных точек. И фиксируется первый максимум, который говорит о том, что стержень сжался до критической отметки и начинает терять свою прямолинейную форму. Схожая зависимость продольной силы от времени в стержне получается в задаче Хоффа(Рис. 8)

Зависимость критической силы от скорости сжатия при разных температурах

Рис.9 Зависимость критической силы от скорости сжатия

Рис.10 Сравнение результатов с континуальной постановкой задачи

Рис.12 Сравнение результатов с континуальной постановкой задачи

Рис.13 Вторая форма потери устойчивости

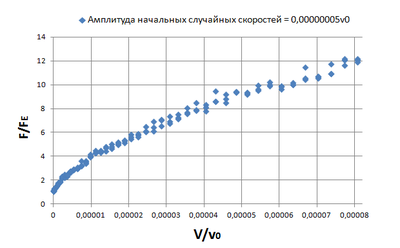
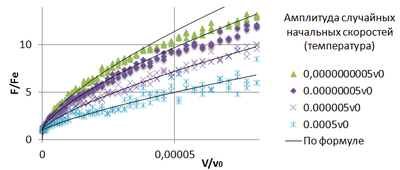
Теперь рассмотрим зависимость критической силы от скорости сжатия стержня с заданной амплитудой случайных начальных скоростей (Рис.9). И для получения размаха проведем несколько реализации, поскольку начальные скорости заданы случайным образом. На данном графике (Рис.9) видно, что при стремлении скорости сжатия к нулю получаем значение критической силы равной силе Эйлера (Fe). Показан тот факт, что действительно в динамике значение критической силы можно получить в несколько раз больше статической силы Эйлера. В данном случае в 12 раз больше. Далее строится аналогичная зависимость, но для разных начальных случайных скоростей частиц цепочки (Рис. 10) и сравнивается с решением, полученным в континуальной постановке задачи.

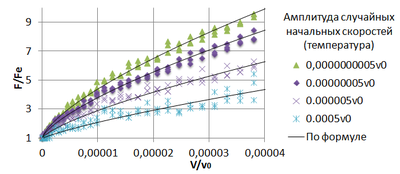
Приведено два графика (Рис.10-11), поскольку стоит отметить, что при локально малых скоростей сжатия видно качественное сходство в полученных результатах и решении задачи Хоффа. При построении графика по формуле (19) подбирался коэффициент d (кривизна) таким образом, чтобы получить максимально близкие значения критических сил к тем, что были определены в данной работе с разными случайными начальными скоростями. Диапозон скоростей сжатия (0 – 0.0002) в заданной конфигурации взят неслучайно. При данных значениях мы получаем первую форму потери устойчивости.

Вторая Форма потери устойчивости

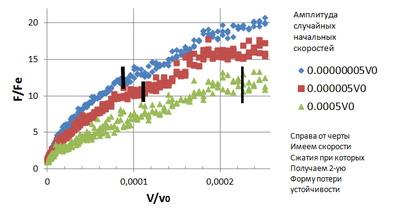
Вторая форма потери устойчивости имеет следующий геометрический вид (Рис.2) Определим, при каких начальных скоростей сжатия получается вторая форма потери устойчивости дискретного стержня. И каким образом на это влияет тепловое движение. Для этого построим зависимость критической силы от начальных скоростей сжатия, взятых в больших диапазонах (Рис.13).

Результаты и выводы работы

В ходе работы были получены следующие результаты:

1. Проведено моделирование потери устойчивости стержня
2. Амплитуда случайных скоростей частиц существенно влияет
на величину критической силы 3. Показано, что зависимость критической силы от скорости сжатия для цепочки при малых скоростях хорошо описывает поведение стержня в континуальной постановке задачи при его сжатии
4. Показано влияние теплового движения на получение второй формы потери устойчивости.

Материалы работы

• Презентация работы(pptx)
• Превью(pdf)
• Плакат(pdf)

Список литературы

[1] Лаврентьев М.А., Ишлинский А.Ю. Динамические формы потери устойчивости упругих систем. Докл. АН СССР, 64, №6, 1949, 779-782
[2] Heinzerling H. Mathematische Behandlung einiger grundlegender Fragen des Knicksproblems des geraden Stabes: Diss., 1938
[3] Попов Е.П. Теория и расчет гибких упругих стержней. Наука, М., 1986
[4] Kuzkin V.A., Dannert M.M. Buckling of a column under a constant speed compression: a dynamic correction to the Euler formula // Acta Mechanica, 227(6), 1645-1652, 2016, DOI: 10.1007/s00707-016-1586-5
[5] Karagiozova,D., Alves,M.: Dynamic elastic-plastic buckling of structural elements: A Review. Applied Mechanics Reviews 61 (2008). doi: 10.1115/1.2939481
[6] Kornev,V.M.: Development of dynamic forms of stability loss of elastic systems under intensive loading over a finite time interval. Journal of Applied Mechanics and Technical Physics 13(4), 536–541 (1974).
[7] Kornev,V.M.: Asymptotic analysis of the behavior of an elastic bar under aperiodic intensive loading, Journal of Applied Mechanics and Technical Physics 13(3), 398–406 (1974).
[8] Markin,A.V.: Buckling in an elastic rod under a time-varying load. Journal of Applied Mechanics and Technical Physics 18(1), 134–138 (1977).
[9] Andrew Noske «Efficient Algorithms for Molecular Dynamics Simulations and Other Dynamic Spatial Join Queries»
[10] Lei Shi, Philip Rohringer «Confined linear carbon chains as a route tobulk carbyne», (2016)
[11] Steven W Cranford «Thermal stability of idealized folded carbyne loops», (2013)