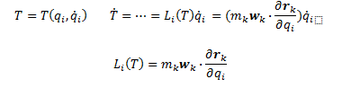Возможные и виртуальные скорости
Дискуссия между Ф.Ф.Прохоренко (ФП) и А.Костаревым (АК).
ФП: Одной из целей моей работы было сокращение в курсе лекций потерь времени на изложение тернистого пути Великих Механиков и их подходов к решению задач. Использование магического термина "возможное перемещение" и его отождествление с понятием вариации (вполне законного в разделе вариационных принципов) считаю ошибкой (методической, по меньшей мере). В самом деле, что общего у δr c вариацией - изменением вида функциональной зависимости? А ведь получают δr умножением некоторой возможной скорости на dt.
АК Это не так.
ФП: Это так. У Гантмахера, если вы помните, ключевыми понятиями являются именно возможные скорости, которые он получает как множество «решений» системы, полученной дифференцированием даже уравнений голономных связей, а разность этих скоростей, умноженных на dt называет виртуальными δr.
АК: Ну и правильно. Разность между двумя возможными скоростями есть виртуальная скорость. Умножать на dt и получать δr не нужно. Достаточно виртуальной скорости, которую (конечную) можно хоть изобразить.
ФП: А впереди еще и виртуальные и действительные …
АК: Термин "возможное перемещение" конечно неудачен лингвистически. При движущихся связях (есть - таки нестационарные связи) есть возможные скорости, определяемые множеством начальных условий.
ФП: Поэтому у меня все скорости возможные в прямом смысле этого слова ,
АК: Что значит прямой смысл? Какой еще бывает?
ФП: Это означает, что после введения величин, однозначно описывающих движение тела ( обобщенных координат) они могут изменяться как угодно, поскольку они и были введены с учетом т.н. связей , причем неголономные связи никак не влияют на описание положения, а будут приняты во внимание в описанной мною формулировке теоремы - частном случае закона баланса энергии, которому глубоко начхать ( простите) на все придумываемые нами термины.
АК: Мы говорим либо о разных вещах, либо на разных языках. Надо бы начать с терминов. Я называю возможными абсолютные скорости, Вы – относительные, даже, скорее, обобщенные.
ФП: А действительные мы получим , решив на основе трех ФЗМ поставленную задачу, причем замечу , что и Вы при составлении уравнений даже и не вспоминаете , что вы подразумеваете под символом V - возможную, действительную или , не дай бог, виртуальную скорости. Вы же, Алексей Владимирович, не в упрек вам будет сказано, ввели еще одну виртуальную скорость.
АК: У меня написано : «Силы и связи определяют множество возможных абсолютных скоростей Vk, отвечающих множеству начальных условий. Производные по времени от всех возможных скоростей точки одинаковы и равны Wk. Определенным начальным условиям отвечают действительные абсолютные скорости точек. Далее написан 2й закон, который порождает возможные скорости. На них он и умножен. Теорема справедлива для всех возможных скоростей. Я не ясно выразился? Слово «виртуальный» очень подходит, эти (относительные) скорости не могут совпасть с действительными при нестационарных связях.
ФП: Деление координат на ответственные за «переносное» и за «относительное» движение и на «свободные» и нет ничем не облегчает задачу - на каждую координату можно поставить свой «моторчик» ( в том числе и на относительную).
АК: Студенты уже знакомы с этими понятиями, и их полезно использовать. Раздувающийся шарик, божья коровка ползет по нему и тд, все доступно. Моторчик поставить можно, но его нет. Так можно дойти до отрицания связей и отличия их реакций от нагрузки. Это недопустимо. Есть прямая и обратная задача. Для свободных координат Вы решаете обратную задачу, для остальных- прямую. Понятие нестационарных связей применимо только в случаях, когда инертность системы пренебрежимо мала по сравнению с инертностью связей (движение спичечного коробка по волнам, поезда по Земле, человека по поезду, и т.п.). В противном случае связь должна быть включена в систему. В большинстве задач Мещерского не обращено внимание на это обстоятельство. Поэтому счел нужным в комплексном задании по динамике вычислять силы, приложенные к нестационарной связи, чтобы заставить ее двигаться указанным образом.
ФП: Принцип освобождаемости от связей - еще один ненужный «принцип» . Не проще ли один раз сказать, что все тела действуют друг на друга посредством сил и моментов и писать уравнения нисколько не заботясь о том , стали ли тела «!свободными!»?
АК: Этот принцип не лишний. Его применяют не там, где надо, например, в статике. А вот в принципе возможных скоростей он в самый раз, и Вы его применяете. Среди уравнений, которые получаем, освободив связи, cтолько дифф уравнений, сколько свободных координат. Остальные уравнения- не дифференциальные, хотя имеют их вид. Из них, после интегрирования первых уравнений, находим реакции.
ФП: Я вообще не применяю ПВП в его исходной формулировке в силу описанного мною подхода.
АК: В чем состоит Ваш подход? Можно получить основные тезисы?
ФП: Достаточно сказать , точнее , применить 3-й ФЗМ ( теорему о изменении энергии), чтобы получить, что необходимыми условиями покоя является равенство нулю мощности( т.е равенство нулю обобщенных сил – но это, опять же, излишняя смысловая нагрузка)
АК: Все верно. Но применять его к телу без степеней свободы бессмысленно. Нужно освободиться от связей. Вот где нужен принцип.
ФП: Другой вопрос. По прежнему не считаю нужным делить Т на три части. Но это мы обсудим при встрече.
АК: Попробуйте обойтись без этого в примере с эллипсом.
ФП: Самым коротким, но только для механических связей, мне кажется путь: Освобдились от связей, включили реакции в число активных сил, тогда
АК: Вы хотели сказать: освободить связи! Освобождая нестационарную связь, Вы
- Теряете ее идеальную реакцию. Не освобождая, Вы ее найдете по трем Т.
- Получаете лишние уравнения движения, которые затем игнорируете за ненадобностью. Вы предлагаете
писать уравнения совместного движения Земли и собачки. Не проще ли сразу задать движение Земли, считая, что собачка не может его изменить?
Независимость скобок Li(T) легко объяснить, не освобождая нестационарные связи. Li(T) есть касательные к поверхности движущейся связи ускорения, которые в принципе не могут зависеть от касательных к связи виртуальных скоростей.