Бублий И.Р.: Движение тела-точки в центральном потенциальном поле

Работу выполнил студент кафедры "Теоретическая механика" Бублий Илья (Группа 04).

Руководитель

Руководитель СПбГПУ: д.ф.-м.н Е.А. Иванова

Аннотация

Классическая механика, как метод изучения физических процессов, не имеет внутри себя ограничений на область применения. Естественно, каждая используемая модель имеет ограниченную область применения. Перспективным направлением развития классической механики является создание и использование более сложных базовых моделей. С помощью этих моделей можно описывать явления, ранее считавшиеся неподвластными методу классической механики. Данная работа посвящена описанию движения тела вблизи центра притяжения методами механики Эйлера. В качестве тела используется базовая модель тела-точки, введенная в рассмотрение П.А. Жилиным. Тело-точка общего вида является обобщением модели бесконечно малого абсолютно твердого тела , а соответственно и материальной точки. Тело-точка - это материальный объект, занимающий нулевой объем в пространстве. В отличие от материальной точки, тело-точка совершает не только трансляционные, но и вращательные движения. Фактически, определением тела-точки является задание его кинетической энергии в следующем виде:

[math] K=m(\dfrac{1}{2} \boldsymbol{v}\cdot \boldsymbol{v}+B \boldsymbol{v}\cdot\boldsymbol{\omega}+\dfrac{1}{2}J \boldsymbol{\omega}\cdot\boldsymbol{\omega}) [/math]

Здесь [math]\boldsymbol{v}[/math] - вектор трансляционной скорости, [math]\boldsymbol{\omega}[/math] - вектор угловой скорости, [math]m[/math] - масса тела-точки, [math]B, J[/math] - тензоры инерции тела-точки. Нетрудно видеть, что кинетическая энергия тела-точки имеет такую же структуру, как и кинетическая энергия абсолютно твердого тела. При этом в отличие от твердого тела, тензор [math]B[/math] тела-точки не обязан обладать свойством антисимметричности. Целью данной работы является решение задачи о движении тела-точки вблизи неподвижного центра притяжения, анализ влияния параметров задачи на вид решения, получение пространственных траекторий движения. Полученные результаты могут быть использованы для описания движения планет и спутников, движения заряженных частиц, движения тел в магнитном и электрическом полях, поведение сред, частицы которых имеют вращательные степени свободы. Тем не менее, в основной части работы автор будет оперировать абстрактными механическими величинами без привязки к конкретной области применения.

Постановка задачи

Численно исследовать решение системы нелинейных дифференциальных уравнений (их вывод подробно описан в работе) следующего вида:

[math] \boldsymbol{r}''+\boldsymbol{\Omega}'=-\dfrac{\boldsymbol{r}}{r^3} [/math]

[math] \boldsymbol{r}''+J^* \boldsymbol{\Omega}' =\boldsymbol{\Omega} \times \boldsymbol{r}' [/math]

Начальные условия:

[math] \boldsymbol{r}(0)=\boldsymbol{r_0},\quad \boldsymbol{r}'(0)=\boldsymbol{v_0},\quad \boldsymbol{\Omega}(0)=\boldsymbol{\Omega_0} [/math]

Результаты численных расчетов

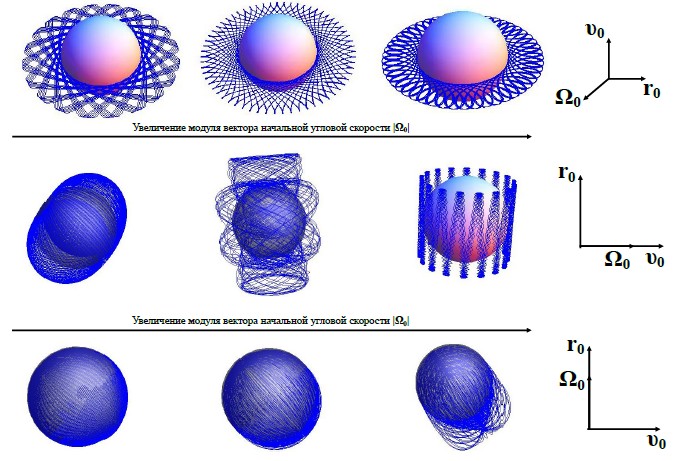
Далее параметр [math]J^*=100[/math]. Соотношение между векторами начального радиуса-вектора и начальной скорости выбрано таким, при котором материальная точка двигалась бы по окружности. Рассмотрены три варианта направления вектора начальной угловой скорости [math]\boldsymbol{\Omega_0}[/math]. В каждом случае варьировался его модуль.

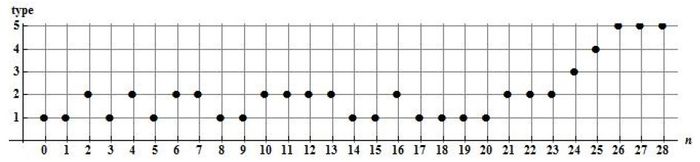
Зависимость характера траектории от параметра [math]B \cdot m=10^n[/math] кг[math] \cdot[/math] м

Система Земля-Луна

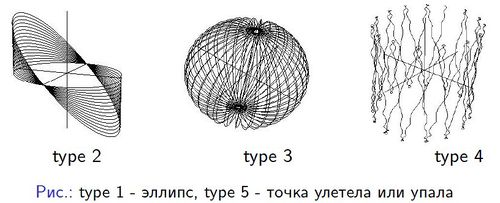
Расчеты проводились для параметров задачи о движении Луны вокруг Земли. Дополнительный параметр [math]B \cdot m[/math] варьировался в широких пределах. При значениях [math]B \cdot m[/math] порядка [math]10^{22}[/math] кг [math]\cdot[/math]м траектория тела-точки напоминает о колебаниях угла наклона плоскости орбиты Луны к плоскости эклиптики (type 2)

Частное решение задачи, [math] |\boldsymbol{K_1}|=const[/math]

Начальные условия должны быть такими, что:

[math] \boldsymbol{v_0}\cdot(\boldsymbol{v_0}+B \boldsymbol{\omega_0})=\dfrac{A}{m |\boldsymbol{R_0}|}, \quad \boldsymbol{R_0}\cdot(\boldsymbol{v_0}+B \boldsymbol{\omega_0})=0 [/math]

В этом случае задача сводится к решению уравнения для [math]|\boldsymbol{R}|[/math]:

[math] \dfrac{d^2 |\boldsymbol{R}|^2}{dt^2}+\dfrac{B^2 |\boldsymbol{K_1}|^2}{m^2 (J-B^2)^2}|\boldsymbol{R}|^2 - \dfrac{2 J A}{m (J-B^2)}\dfrac{1}{|\boldsymbol{R}|}=\dfrac{B^2 (|\boldsymbol{K}|^2+|\boldsymbol{K_2}|^2)-2 J^2 |\boldsymbol{K_1}|^2}{m^2 (J-B^2)^2} [/math]

Начальные условия:

[math] |\boldsymbol{R}||_{t=0}=|\boldsymbol{R_0}|, \quad \dfrac{d|\boldsymbol{R}|}{dt}|_{t=0}=\dfrac{\boldsymbol{v_0}\cdot \boldsymbol{R_0}}{|\boldsymbol{R_0}|} [/math]

Для частного решения доказаны следующие факты:

1. Если [math]\boldsymbol{R_0}\cdot\boldsymbol{v_0}=0[/math], траектория - окружность, [math]|\boldsymbol{R}|=const[/math].

Если [math]\boldsymbol{R_0}\cdot\boldsymbol{v_0} \ne 0[/math], траектория - пространственная кривая.

При любых начальных условиях [math]|\boldsymbol{R}| \ne const[/math]

2. Пусть [math]\boldsymbol{R_0}\cdot\boldsymbol{v_0} \ne 0[/math]. Введем обозначение [math]Cos \beta = \dfrac{\boldsymbol{K_1}\cdot\boldsymbol{K_2}}{|\boldsymbol{K_1}||\boldsymbol{K_2}|}[/math]

Из интеграла энергии: [math]\dfrac{1}{|\boldsymbol{R}|}=\dfrac{1}{|\boldsymbol{R_0}|}+\dfrac{2 B |\boldsymbol{K_1}||\boldsymbol{K_2}|}{A m (J-B^2)}(Cos \beta-Cos \beta_0)[/math]

Тогда [math] R_1 \le |\boldsymbol{R}|\le R_2 [/math], где [math] \dfrac{1}{R_1}-\dfrac{1}{R_2} =\dfrac{2 B |\boldsymbol{K_1}||\boldsymbol{K_2}|}{A M (J-B^2)} [/math]

Результаты численных расчетов

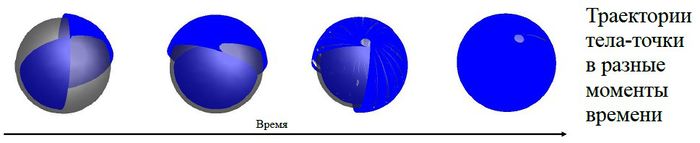
Параметры задачи выбраны так, чтобы траектории тела-точки находились в тонком концентрическом шаровом слое, подобном электронному облаку в атоме водорода.

Основные результаты

Исследованы зависимости радиуса вектора, количества движения и собственного кинетического момента от начальных условий и параметра [math]J^*[/math].

Установлено, что возможно движение, при котором угол наклона плоскости орбиты тела-точки к плоскости, ортогональной вектору полного кинетического момента, совершает колебания, подобные колебаниям угла наклона плоскости орбиты Луны к плоскости эклиптики.

Установлено, что существуют траектории, лежащие в сферическом слое, аналогичном электронной орбитали вокруг атома водорода в невозбужденном состоянии. Найдены параметры, регулируя которые можно менять толщину этого слоя.