Тепловые колебания в одномерном кристалле

Научный руководитель

Доктор физ.-мат. наук, зав. каф. "Теоретическая механика" А.М. Кривцов

Аннотация

• В работе рассмотрен одномерный кристалл с нелинейным взаимодействием частиц (кубическая нелинейность в силе взаимодействия). Получено численное решение следующих задач: исследование колебаний кинетической энергии при начальном равномерном задании кинетической температуры по кристаллу и исследование колебаний кинетической температуры при задании синусоидального профиля кинетической температуры кристалла. Получено, что зависимость кинетической энергии и кинетической температуры одномерного кристалла от времени носит колебательный характер и с увеличением нелинейности взаимодействия скорость затухания колебаний увеличивается. Предложена аппроксимация полученных законов затухания для различной нелинейности взаимодействия. Получено хорошее соответствие предложенной аппроксимации при малой нелинейности для различных начальных условий. Данный факт может свидетельствовать о том, что аналитическое решение, полученное ранее в [10] не нарушается при введении малой нелинейности. Проведено сравнение зависимости законов затухания от нелинейности для двух рассмотренных задач. Показано различие в законах затухания.

Актуальность

• Актуальные на сегодняшний день научные труды [1 – 3] посвящены исследованию процессов, протекающих в идеальных кристаллах. Такие кристаллы обладают свойствами отличными от повсеместно применяемых материалов с дефектами. Однако до недавнего времени, получить материалы без дефектов было невозможно.
• Существующие модели, описывающие термомеханические процессы в идеальных структурах, не позволяют получить удовлетворительного соответствия с результатами, наблюдаемыми в экспериментах. Так, например, при исследовании процесса теплопроводности в экспериментах с углеродистыми нанотрубками наблюдается отклонение от закона Фурье [4 – 6]. Известно, что и в простейших дискретных системах, таких как одномерный кристалл, распространение тепла не подчиняется закону Фурье [7 – 11]. В частности, если в начальный момент времени частицы линейного одномерного кристалла упорядочены, а их скорости заданы случайно, то начинается колебательный процесс перехода кинетической энергии в потенциальную энергию. Этот переход заканчивается распределением внутренней энергии между кинетическими и деформационными степенями свободы, определяемым теоремой о вириале. В работе [10] также получено аналитическое решение, позволяющее определить колебания кинетической и потенциальной энергии в линейном одномерном кристалле через функцию в Бесселя первого рода. Однако в случае нелинейного взаимодействия между частицами – аналитического решения нет.
• В работе рассмотрен одномерный кристалл с нелинейным взаимодействием частиц. Получено численное решение следующих задач: исследование колебаний кинетической энергии при начальном равномерном задании кинетической температуры по кристаллу и исследование колебаний кинетической температуры при задании синусоидального профиля кинетической температуры кристалла.

Нелинейный кристалл

Рассматривается одномерный кристалл: цепочка одинаковых частиц массы [math]m[/math], с линейным коэффициентом [math]\C_1[/math] и нелинейным [math]\C_2[/math]. В выражении для силы взаимодействия сохраняется линейное и кубическое слагаемое. Уравнение динамики цепочки имеет вид:

[math] \ddot u_k =C_1(u_{k-1}-2u_k+u_{k+1}) + C_2((u_{k+1}-u_k)^3 - (u_k-u_{k-1})^3) ~~~~~ (1) [/math]

где [math]u_k[/math]– перемещение [math]k[/math] – й частицы; [math]k[/math] – индекс, принимающий произвольные целые значения.

Принимались периодические граничные условия:

[math] {u_{k+N} =u_k, ~~~ N\gt \gt 1 } ~~~~~ (2) [/math]

где [math] N[/math] – число независимых частиц.

Для оценки влияния нелинейности введен безразмерный параметр [math] \alpha [/math], позволяющий определить вклад нелинейного взаимодействия на колебания энергии в цепочке.

Колебания кинетической энергии

Для решения уравнения (1) заданы начальные условия в виде:

[math] u_n = 0, ~~~~~ u_n =ρ_n, ~~~~ 0 ≤ n ≤ N ~~~~~ (3) [/math]

где [math] n [/math] – номер частицы, [math] ρ_n [/math] – случайная величина, полученная с помощью генератора случайных чисел. Подобное задание начальных условий аналогично распределению равномерной температуры по кристаллу Введем удельную (приходящуюся на одну частицу кристалла) кинетическую энергию:

[math] K=m\left \langle {\dot u_k^2} \right \rangle ~~~~~ (4) [/math]

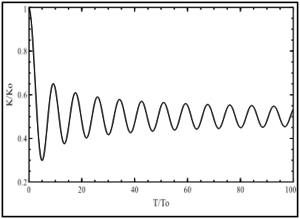
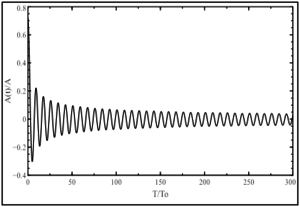
Для анализа зависимости кинетической энергии от параметра α были проведены численные эксперименты для одномерного кристалла с нелинейным взаимодействием частиц (1) с начальными условиями (3) и граничными условиями (2). Здесь и далее кинетическая энергия была обезразмерена по начальной заданной кинетической энергии, а время расчётов – по отношению к периоду колебаний частицы вблизи положения равновесия. На рис. 1 представлены результаты численного моделирования задачи об определении кинетической температуры одномерного кристалла с нелинейным взаимодействием.

а) б)

Рис. 1. Зависимость колебаний кинетической энергии в кристалле: [math] а)~ \alpha=0 [/math] , [math] б)~ \alpha=1 [/math]

Анализируя результаты, представленные на рис. 1 можно сделать вывод о том, что скорость затухания колебаний увеличивается при увеличении нелинейности, а период колебаний – уменьшается. Нелинейность во взаимодействии частиц одномерной цепочки позволяет кинетической энергии кристалла релаксировать быстрее, вследствие чего вся система приходит в состояние термодинамического равновесия.

Для линейного взаимодействия между частицами в работе [10] было получено, что колебания кинетической энергии затухают со скоростью [math] \sqrt{t} [/math]. Для случая нелинейного взаимодействия частиц одномерного кристалла, скорость затухания колебаний кинетической энергии и зависимость этого закона затухания от нелинейности неизвестна. В связи с этим, необходимо исследовать закон затухания кинетической энергии в зависимости от параметра нелинейности.

Вид затухающей функции определён в классе функций:

[math] g(t/T_0)=a(t/T_0)^{-b} ~~~~~~~~~~~ (5) [/math]

где [math] a,b [/math] – неизвестные параметры, варьируя которые, можно получить функцию, график которой наиболее точно ложится на график затухания кинетической энергии. Среднее значение кинетической энергии при определении закона затухания не учитывается.

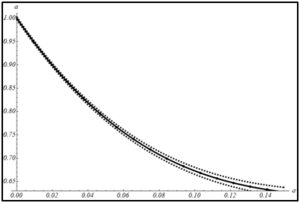
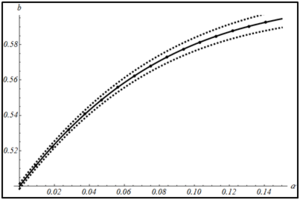
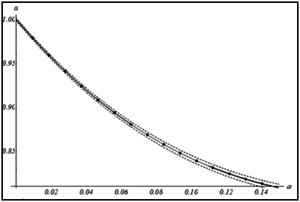
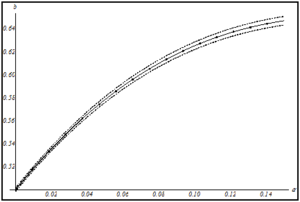
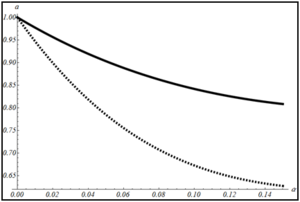
Исследована зависимость параметров в законе затухания кинетической энергии при малой нелинейности. Выдвинуто предположение, что закон затухания не должен сильно меняться при введении малой нелинейности во взаимодействие. Результаты численного моделирования представлены на рис. 2.

а) б)

Рис. 2. Зависимость а) параметра [math] a [/math] и б) параметра [math] b [/math] закона затухания от параметра нелинейности α. Штриховыми линиями отмечен доверительный интервал для значений коэффициентов.

Полученные результаты показывают, что при увеличении нелинейности взаимодействия частиц, значения параметров закона изменяются разнонаправлено. Так значение показателя степени в законе затухания [math] b [/math] увеличивается, а коэффициента [math] a [/math] - уменьшается.

В результате получено, что при малой нелинейности отличие в значениях параметров закона затухания от случая линейного взаимодействия составляет не более 10%, что подтверждает выдвинутое ранее предположение и может свидетельствовать об устойчивости известного аналитического решения [10]. Также установлено, что выбранный вид закона затухания дает хорошее соответствие при малой нелинейности. Однако при большой нелинейности предложенная аппроксимация не дает точного соответствия.

Для полученных зависимостей параметров закона затухания от нелинейности предложена аппроксимация в виде степенных функций. Для коэффициента [math] a [/math] получена следующая зависимость: [math] a(\alpha)=0.004{\alpha}^{-2}+0.57 [/math] Для показателя степени [math] b [/math] аппроксимация имеет следующий вид: [math] b(\alpha)=-4{\alpha}^{-2}+1.2\alpha+0.5 [/math]

Полученные результаты показывают, что зависимость степени [math] b [/math] и коэффициента [math] a [/math] в законе затухания от параметра нелинейности α является нелинейной. Установлено, что предложенная аппроксимация закона затухания дает хорошее соответствие при малой нелинейности. При рассмотрении малой нелинейности отличие в значениях параметров закона затухания от случая линейного взаимодействия составляет не более 20%. Предложена полиномиальная аппроксимация для зависимости параметров закона затухания от введенной нелинейности.

Колебания кинетической температуры

Как показано ранее, увеличение нелинейности взаимодействия частиц приводит к увеличению скорости затухания кинетической энергии в одномерном кристалле. Высокочастотные колебания наблюдают и при задании начального синусоидального распределения температуры по кристаллу. Синусоидальное распределение температуры можно представить как случай неравномерного нагрева материала по его длине. В этом случае инициализируется колебательный процесс, связанный со стремлением кинетической температуры равномерно распределиться по кристаллу. При этом колебания амплитуды профиля заданной температуры со временем будут затухать.

Для исследования распределения кинетической температуры в нелинейном одномерном кристалле (1) с периодическими граничными условиями (2), рассмотрены следующие начальные условия:

[math] u_n = 0, ~~~~~ u_n =ρ_n σ(х), ~~~~ x=na ~~~~~ (6) [/math]

где [math] n [/math] – номер частицы, [math] a [/math] – расстояние между ними, [math] ρ_n [/math] – случайная величина с равномерным распределением, а [math] σ(х) [/math] - начальные распределения скоростей частиц в цепочке. Величину [math] σ(х) [/math] определим так, чтобы получить начальное распределение температуры по синусоидальному закону:

[math] σ^2(х)=A\sin{(\kappa x)} + \overline{T} ~~~~~ (7) [/math]

где [math] A [/math] и [math] \kappa [/math] – константы, [math] \kappa=2\pi / N [/math], [math] \overline{T} [/math] – значение средней кинетической температуры в одномерном кристалле.

Определен способ вычисления колебаний амплитуды синусоидальной температуры через разложение кинетической температуры одномерной цепочки в ряд Фурье. Для этого вычислен первый коэффициент при разложении кинетической температуры в ряд Фурье.

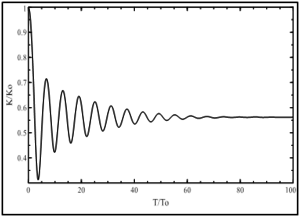
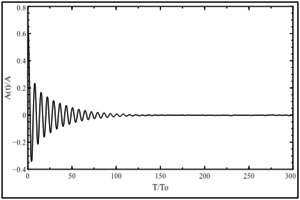
Для проведения исследований зависимости колебаний амплитуды кинетической температуры кристалла, от параметра α проведена серия численных экспериментов для одномерного кристалла с нелинейным взаимодействием частиц (1) с начальными условиями (6), (7) и граничными условиями (2). Амплитуда обезразмерена по начальной амплитуде [math] A [/math]. Результаты представлены на рис. 3.

а) б)

Рис. 3. Зависимость колебании амплитуды синусоидального профиля температуры от времени в одномерном кристалле: [math] а)~ \alpha=0 [/math] , [math] б)~ \alpha=2 [/math]

Анализируя результаты моделирования, полученные выше, можно сделать вывод о том, что скорость затухания колебаний амплитуды температуры увеличивается при увеличении коэффициента нелинейности α, а период колебаний – уменьшается.

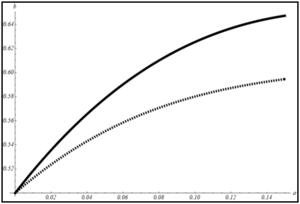
Получены параметры аппроксимации закона затухания (5) амплитуды кинетической температуры для различного значения параметра нелинейности. Показано, что выбранный вид закона затухания (5) дает хорошее соответствие при малой нелинейности, однако при большой нелинейности предложенная аппроксимация не дает точного соответствия. Как было отмечено ранее, для колебаний кинетической энергии одномерного кристалла, при малой нелинейности закон затухания меняется мало. Для проверки того, будет ли выполнятся это для колебаний амплитуды температурного профиля, были проведены исследования закона затухания амплитуды синусоидального профиля температуры при малой нелинейности. Результаты численного эксперимента представлены на рис.4.

а) б)

Рис. 4. Зависимость а) параметра [math] a [/math] и б) параметра [math] b [/math] закона затухания от параметра нелинейности α при синусоидальном задании температуры.

Полученные результаты показывают, что при увеличении нелинейности взаимодействия частиц значения параметров закона изменяются разнонаправлено. Так значение показателя степени в законе затухания [math] b [/math] увеличивается, а коэффициента [math] a [/math] - уменьшается. Также следует отметить, что при малой нелинейности, отличие в значениях параметров закона затухания от случая линейного взаимодействия составляет не более 15%.

Для полученных зависимостей коэффициентов закона затухания от нелинейности предложена аппроксимация в виде полиномиальных функций. Для коэффициента [math] a [/math] была получена следующая зависимость: [math] a(\alpha)=0.002{\alpha}^{-2}+0.8 [/math]. Для показателя степени [math] b [/math] аппроксимация имеет следующий вид: [math] b(\alpha)=-4.6{\alpha}^2+1.7\alpha+0.5 [/math].

В результате можно сделать вывод, что зависимость показателя степени [math] b [/math] и коэффициента [math] a [/math] в законе затухания от параметра нелинейности α является нелинейной. Предложена аппроксимация зависимостей параметров закона затухания от нелинейности. Установлено, что закон затухания зависит от нелинейности. При исследовании малой нелинейности, отличие в значениях параметров закона затухания от случая линейного взаимодействия составляет не более 15%.

Сравнение зависимостей параметров двух законов затухания от нелинейности

В двух рассмотренных задачах были определены законы затухания колебаний кинетической энергии и амплитуды кинетической температуры в одномерном нелинейном кристалле. Закон затухания для обеих величин определялся в виде степенных функций. Определены два параметра для каждого из законов затухания и установлены их зависимости от введенной нелинейности.

При этом остается вопрос, как отличается зависимость этих параметров от нелинейности для кинетической энергии и кинетической температуры. Также известно, что в случае линейного одномерного кристалла закон затухания для колебаний кинетической энергии и амплитуды синусоидального профиля температуры идентичен. Для решения этого вопроса проведены сравнения зависимостей параметров от нелинейности в двух законах затухания. Результаты представлены на Рис. 5.

а) б)

Рис. 5. Зависимость а) параметра [math] a [/math] и б) параметра [math] b [/math] закона затухания от нелинейности (кинетическая энергия - сплошная линия, кинетическая температура - штриховая)

Из представленных результатов можно сделать вывод о том, что зависимость параметра [math] a [/math] в законе затухания для колебания кинетической энергии и амплитуды кинетической температуры имеют схожий вид. Результаты, представленные на рис. 5, показывают, что показатели степени ([math] b [/math]) в законе затухания в двух рассмотренных задачах имеют схожий вид зависимости от параметра нелинейности, однако значения параметров отличаются друг от друга на 20%. Коэффициент а, для двух рассмотренных величин имеет нелинейную зависимость от параметра α, при этом значения коэффициентов двух законов затухания отличаются на 30%. Таким образом, установлено различие в законах затухания при рассмотрении нелинейного взаимодействия.

Заключение

• В работе исследован одномерный кристалл с нелинейным взаимодействием частиц (кубическая нелинейность в выражении для взаимодействия силы). Для проведения исследования введен безразмерный параметр [math] \alpha [/math], характеризующий отношение влияния линейного и нелинейного взаимодействия между частицами одномерного кристалла. Рассмотрены две постановки начальных условий: равномерное задание температуры и синусоидальный профиль температуры в одномерном кристалле.
• Для первой постановки задачи исследована кинетическая энергия кристалла и ее зависимость от параметра нелинейности [math] \alpha [/math]. Получено, что зависимость кинетической энергии одномерного кристалла от времени носит колебательный характер и с увеличением нелинейности скорость затухания колебаний увеличивается. Предложена аппроксимация закона затухания кинетической энергии кристалла для различного значения параметра нелинейности α. Введённая аппроксимация дает хорошее соответствие для малой нелинейности, при большой нелинейности наблюдается расхождение графика колебаний энергии и закона затухания.
• Хорошее соответствие предложенной аппроксимации при малой нелинейности для случая равномерного задания температуры может свидетельствовать о том, что аналитическое решение не нарушается при введении малой нелинейности. Таким образом, можно сделать вывод об устойчивости аналитического решения, полученного в [10].
• Для второй постановки задачи (синусоидальной профиль температуры кристалла) исследована зависимость кинетической температуры кристалла от параметра нелинейности [math] \alpha [/math]. Показано, что зависимость амплитуды кинетической температуры кристалла от времени также носит колебательный характер и с увеличением нелинейности скорость затухания колебаний увеличивается. Введена аппроксимация закона затухания амплитуды температурного профиля кристалла для различного значения параметра нелинейности α. Предложенная аппроксимация дает хорошее соответствие для малой нелинейности. При большой нелинейности также наблюдается расхождение графика колебаний амплитуды и закона затухания.
• Проведено сравнение зависимостей параметров закона затухания от параметра нелинейности для двух начальных условий (равномерная температура и синусоидальный профиль температуры). Показано различие в законах затухания для двух рассмотренных начальных условий.

Литература

1. Кривцов А.М. Деформирование и разрушение твердых тел с микроструктурой. М.: Физматлит, 2007. 304 с.
2. Упругие и тепловые свойства идеальных кристаллов: учеб. пособие / И. Е. Беринский [и др.] ; под ред. А. М. Кривцова. - СПб.: Изд-во Политехн. ун-та, 2009. - 144 с.
3. Кривцов А.М., Ле-Захаров А.А. Исследование процесса теплопроводности кристаллах с дефектами методами молекулярной динамики// ДАН. 2008. Т. 420. № 1. С. 45 – 49.
4. E. Brown, L. Hao, J.C. Gallop, J.C. Macfarlane. Ballistic thermal and electrical conductance measurements on individual multiwall carbon nanotubes. Appl. Phys. Lett. (2005) 87, 023107.
5. Zhaohui Wang, Jeffrey A. Carter, Alexei Lagutchev, Yee Kan Koh, Nak-Hyun Seong, David G. Cahill, Dana D. Dlott. Ultrafast Flash Thermal Conductance of Molecular Chains. Science (2007) Vol. 317 no. 5839 pp. 787-790.
6. C. W. Chang, D. Okawa, H. Garcia, A. Majumdar, and A. Zettl. Breakdown of Fourier’s Law in Nanotube Thermal Conductors. Phys. Rev. Lett. (2008) 101, 075903.
7. Giardina C., Livi R., Politi A., Vassalli M. // Phys. Rev. Lett. 2000. V. 84. № 10. P. 2144–2147.
8. Lepri S., Livi R., Politi A. // Phys. Rev. Lett. 1997. V. 78. № 10. P. 1896–1899.
9. Ландау Л.Д., Лифшиц Е.М. Механика. Т. 1. Теоретическая физика. М.: Физматлит, 2004. 224 с.
10. Кривцов А.М. Колебания энергий в одномерном кристалле ДАН. 2014, том 458, № 3, с. 279–281.
11. Andrei A. Gusev, Sergey A. Lurie, Wave-relaxation duality of heat propagation in Fermi–Pasta–Ulam chains // Mod. Phys. Lett. B August 2012, Vol. 26, No. 22