А.М. Кривцов >
Теоретическая механика >
Курсовые проекты 2013 >
Диск Эйлера
Курсовой проект по Теоретической механике
Исполнитель: Соколов Алексей
Группа: 07 (20510)
Семестр: весна 2013
Аннотация проекта[править]
Диск Эйлера – это твёрдое цилиндрическое тело, имеющее единственную точку контакта с горизонтальной поверхностью, по которой он одновременно и катится, и вращается.
Этой простой
механической системе присущи две любопытные особенности — быстрое возрастание звуковой частоты в процессе контакта диска и поверхности на финальном этапе движения, а также
последующая внезапная остановка движения. Эти эффекты может наблюдать каждый, раскрутив на столе обыкновенную монету: «потеряв равновесие», монета окажется лежащей на столе
плашмя, при этом финальная стадия ее движения, когда ее плоскость почти горизонтальна, сопровождается характерным «дрожанием». Однако физическое объяснение этого своеобразного
поведения оказалось сложной задачей, решение которой еще требует дальнейших экспериментальных и теоретических исследований.
Постановка задачи[править]
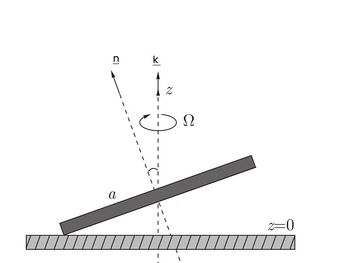
Рассмотрим стационарное движение твердого диска с одной точкой касания без диссипаций.
Для описания тела будем использовать единичный вектор нормали [math] \underline{n} [/math] и вектор [math] \underline{a} [/math] , находящегося в плоскости диска с длиной, равной радиусу диска.
Общие сведения по теме[править]
Повышенный интерес к диску Эйлера возник после опубликования работы К. Моффатта,
в которой резкое прекращение движения диска объясняется прежде всего воздействием силы
вязкого сопротивления воздуха. Эта теория вызвала значительную дискуссию и развитие
конкурентных гипотез о природе основного механизма диссипации энергии для диска Эйлера.
Ван ден Энг (van den Engh) с соавторами провели некоторые эксперименты по движению дископодобных тел, свидетельствующие не в пользу гипотезы о вязком трении. В ответ на работу
Моффатта они опубликовали свое объяснение, ключевым пунктом которого является наличие
скольжения при контакте диска и поверхности. Критика выводов и краткое обсуждение
возможных источников диссипации содержатся также в неопубликованной заметке Э. Руины.
Авторами последовавших экспериментальных и теоретических работ исследовался вопрос
о наличии и степени влияния определенных типов трения на различных этапах движения диска. Были численно и аналитически исследованы модели системы с различными ограничениями, проведен анализ полученных экспериментальных данных. Эти исследования в основном указывают на то, что основными диссипативными силами, вызывающими вибрацию и
остановку диска, являются силы трения качения и трения скольжения, нежели силы вязкого
трения. Из немногих предположений о физике этих эффектов стоит упомянуть, как наиболее
естественную, гипотезу Кесслера и О’Рейли, что резкая остановка диска происходит в результате потери контакта между диском и поверхностью в процессе вибраций при малом угле
наклона диска. (Для проверки этой гипотезы потребуется рассматривать деформируемую модель для контактирующих тел.)
Запишем кинетический момент сиcтемы:
[math] \dot{\underline{K}} = \dot{ \left( \underline{\underline{\Theta}} \cdot \underline{\omega} \right) } = \underline{M} [/math]
[math] \dot{\underline{K}} = \Theta_{12} \underline{n} \times \ddot{\underline{n}} + \Theta_3 \dot{ \left(\Omega \underline{n} \right) } [/math]
Положим
[math] \eta = \underline{k} \cdot \underline{n} = \cos(\vartheta) [/math]
[math] \varepsilon = \underline{k} \times \underline{n} = \sin(\vartheta) [/math]
Имеем далее
[math]\left\{
\begin{array}{lcl}
\underline{a} \perp \underline{k} \times \underline{n} \\
\underline{a} \perp \underline{n} \\
\end{array}
\right. [/math]
Из этого следует:
[math] \underline{a} \parallel \left[ \underline{n} \times ( \underline{k} \times \underline{n}) \right ] [/math]
Имеем
[math] \underline{n} \times ( \underline{k} \times \underline{n} ) = \underline{k} ( \underline{n} \cdot \underline{n}) - \underline{n} (\underline{n} \cdot \underline{k}) = \underline{k} - \eta \underline{n} [/math]
Таким образом можем представить вектор [math] \underline{a} [/math] следующим образом:
[math] \underline{a} = \lambda( \underline{k} - \eta \underline{n}) [/math]
Имеем далее:
[math] a^2 = \lambda^2(1 - \eta^2) = \lambda^2 \varepsilon [/math]
Таким образом
[math] \lambda = \frac{a}{ \sqrt{1 - \eta^2} } [/math]
Недтрудно понять что вектор [math] \underline{a} [/math] в таком случае записывается в следующем виде:
[math] \underline{a} = \frac{a}{ \sqrt{1 - \eta^2} } ( \underline{k} - \eta \underline{n}) [/math]
Имеем далее:
[math] \frac{ \underline{a} } {a} = \frac{ \underline{k} - \eta \underline{n} } { \left| \underline{k} - \eta \underline{n} \right| } [/math]
Получаем таким образом:
[math] \underline{a} = \frac{a}{\varepsilon} (\underline{k} - \eta \underline{n}) [/math]
Теперь запишем соотношения для сил и моментов:
[math] m \ddot{\underline{r}} = m \underline{g} + \underline{N} = (N - mg) \underline{k} [/math]
[math] \dot{ \left( \underline{\underline{O}} \cdot \underline{w} \right) } = \underline{a} \times \underline{N} [/math]
[math] \underline{N} = N \underline{k} [/math]
Таким образом имеем:
[math] \underline{a} \times \underline{N} = \frac{a \eta}{ e} N \underline{k} \times \underline{n} [/math]
В результате получаем систему, описывающую движение тела:
[math]\left\{
\begin{array}{lcl}
\Theta_{12} \underline{n} \times \ddot{\underline{n}} + \Theta_3 \dot{ \left(\Omega \underline{n} \right) } + a \frac{\eta}{\varepsilon} N \underline{n} \times \underline{k} = 0\;(1)\\
m \ddot{z} = N - mg \\
z = - a \varepsilon \\
\end{array}
\right. [/math]
Будем искать решение для стационарного движения:
[math]\left\{
\begin{array}{lcl}
\underline{\omega} = \dot{\psi} \underline{k} + \dot{\varphi} \underline{n} \\
\underline{\omega} \times \underline{a} = 0
\end{array}
\right. [/math]
Тогда:
[math] \dot{ \underline{n}} = \dot{\psi} \underline{k} \times \underline{n} [/math]
[math] \ddot{ \underline{n}} = (\dot{\psi} )^2 \left( \underline{k}\cos{\vartheta} - \underline{n} \right) [/math]
[math] \Omega = \underline{ \omega } \cdot \underline{n} = \dot{ \psi } \cos( \vartheta ) + \dot{ \phi } [/math]
[math] \dot{\left( \Omega \underline{n} \right)} = \Omega \dot{ \underline{n}} = \Omega \dot{ \psi } \underline{k} \times \underline{n} [/math]
Подставляем полученные выражения в уравнение (1)
[math] \left[ -\Theta_{12}(\dot{\psi} )^2 \cos\vartheta - \Theta_3 (\dot{\psi} )^2 \cos\vartheta - \Theta_3 \dot{\phi}\dot{\psi} + a \cot \vartheta N \right] \underline{n} \times \underline {k} = 0 [/math]
Получаем уравнение:
[math]-\Theta_{12}(\dot{\psi} )^2 \cos\vartheta - \Theta_3 (\dot{\psi} )^2 \cos\vartheta - \Theta_3 \dot{\phi}\dot{\psi} + a \cot \vartheta N = 0 [/math]
получаем:
[math] \underline{\omega} \times \underline{a} = 0 [/math]
[math] \left( \dot{\psi} \underline{k} + \dot{\varphi} \underline{n}\right) \times \underline{a} = 0 [/math]
[math] \dot{\psi} \underline{k} \times \underline{a} + \dot{\varphi} \underline{n} \times \underline{a} = 0 [/math]
[math] a \left( \dot{ \psi } \cot( \vartheta) + \frac{ \dot{ \varphi } } \sin( \vartheta) \right) = 0 [/math]
Получаем систему:
[math]\left\{
\begin{array}{lcl}
-\Theta_{12}(\dot{\psi} )^2 \cos\vartheta - \Theta_3 (\dot{\psi} )^2 \cos\vartheta - \Theta_3 \dot{\phi}\dot{\psi} + a \cot \vartheta N = 0 \\
m \ddot{z} = N - mg; z = - a \sin( \vartheta ) \\
\dot{ \psi } \sin( \vartheta ) + \dot{ \varphi } = 0
\end{array}
\right. [/math]
Имеем: [math] \ddot{z} = 0 [/math]
Таким образом [math] N = mg [/math]
Имеем
[math] -(\dot{\psi} )^2 \cos \vartheta ( \Theta_3 + \Theta_{12} ) - \Theta_3 (\dot{\psi} )^2\sin\vartheta + a \cot \vartheta N = 0 [/math]
Получаем следующую зависимость:
[math] \dot{ \psi } = \sqrt{ \frac{a m g \cot( \vartheta)}{ \sin\vartheta \Theta_3 + \cos\vartheta\left( \Theta_{3} + \Theta_{12} \right) } } [/math]
Обсуждение результатов и выводы[править]
В результате работы найден простой метод описания данной динамической системы, получено уравнение стационарного движения. Получена зависимость угловой скорости прецесси [math] \dot{\psi} [/math] от угла [math] \vartheta [/math] между нормалью с плоскости диска и вертикалью .
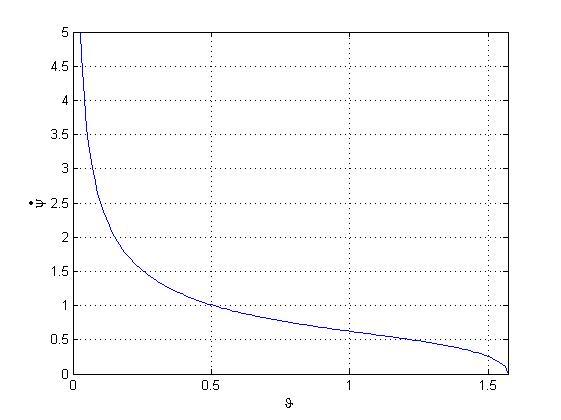
Зависимость угловой скорости прецессии [math] \dot{\psi} [/math] от угла [math] \vartheta [/math] между нормалью к плоскости диска и вертикалью
Ссылки по теме[править]