Dzenushko Dainis. Course project for theoretical mechanics "Double pendulum" — различия между версиями
Dainis (обсуждение | вклад) (Новая страница: «== Subject == Specification of double pendulum oscillations == Task == Rod is connected to the roof by cylindrical joint. The second rod is connected to the end of...») |
Dainis (обсуждение | вклад) |
||
| (не показано 8 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| + | [[Дзенушко Дайнис. Курсовой проект по теоретической механике|Русская версия ]][[Файл:RUS.jpg]] | ||
== Subject == | == Subject == | ||
Specification of double pendulum oscillations | Specification of double pendulum oscillations | ||
| Строка 5: | Строка 6: | ||
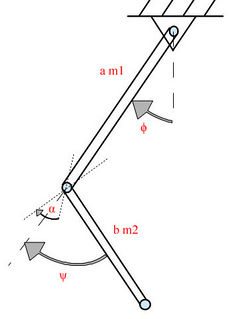
Rod is connected to the roof by cylindrical joint. The second rod is connected to the end of the first rod via cylindrical joint so that when both rods are vertical the angle between joint's axis equals to <math>\alpha</math>. Dissipative forces are not taken to account.<br> | Rod is connected to the roof by cylindrical joint. The second rod is connected to the end of the first rod via cylindrical joint so that when both rods are vertical the angle between joint's axis equals to <math>\alpha</math>. Dissipative forces are not taken to account.<br> | ||
'''System parameters:''' <br> | '''System parameters:''' <br> | ||
| − | # | + | #Inertia tensor of first and second rods are equal. <math>\underline{\underline{\Theta}}_1</math> and <math>\underline{\underline{\Theta}}_2</math> respectively. |
| − | # | + | #length of rods are a and b, their masses <math>m_1</math> and <math>m_2</math> for first and second rods. |
| − | # | + | #Angle between rotation axis of joints equals to <math>\alpha</math><br> |
| − | *<math>\varphi</math> - | + | *<math>\varphi</math> - angle between first rod and vertical direction |
| − | *<math>\psi</math> - | + | *<math>\psi</math> - angle between axis of first and second rods that means the angle in second joint relative to vertical orientation of system. |
<gallery widths=231px heights=319px perrow = 1> | <gallery widths=231px heights=319px perrow = 1> | ||
Файл:2_oscillator.jpg | Файл:2_oscillator.jpg | ||
</gallery> | </gallery> | ||
| − | ''' | + | '''Main task:'''<br> |
| − | * | + | *find the equation of motion for this double pendulum |
| − | == | + | == Solution == |
| − | ''' | + | '''Let's find the way of solving this problem:''' We are going to solve the problem by using the Lagrange equation:<br> |
<math>\frac{d}{dt}\frac{\partial T}{\partial \dot{q}_i}-\frac{\partial T}{\partial q_i} = -\frac{\partial \Pi}{\partial q_i}+Q_i</math><br> | <math>\frac{d}{dt}\frac{\partial T}{\partial \dot{q}_i}-\frac{\partial T}{\partial q_i} = -\frac{\partial \Pi}{\partial q_i}+Q_i</math><br> | ||
| − | *<math>T</math> - | + | *<math>T</math> - Kinetic energy of system <br> |
| − | *<math>\Pi</math> - | + | *<math>\Pi</math> - Potential energy of system<br> |
| − | *<math>q_i</math> - | + | *<math>q_i</math> - Generalized coordinates<br> |
| − | *<math>\dot{q}_i</math> - | + | *<math>\dot{q}_i</math> - generalized velocities<br> |
| − | *<math>Q_i</math> - | + | *<math>Q_i</math> - generalized non-potential forces<br> |
<br> | <br> | ||
| − | ''' | + | '''Selecting generalized coordinates:''' for generalized coordinates we are going to use angles <math>\varphi</math> and <math>\psi</math> <br> |
| − | * | + | *In this problem we neglect non-potential interactions, so generalized non-potential forces equals to zero.<br> |
| − | ''' | + | '''Calculating potential and kinetic energy of system:''' <math>\Pi_1 , T_1 ; \Pi_2 , T_2 </math> of first and second rods relatively.<br> <math>\Pi = \Pi_1 + \Pi_2</math> - Potential energy of system<br> |
| − | <math>T = T_1 + T_2</math> - | + | <math>T = T_1 + T_2</math> - Kinetic energy of system<br> |
| − | <math>T_1 = \frac{\underline{\omega}_1 \cdot \underline{\underline{\Theta}}_1 \cdot \underline{\omega}_1}{2} = \frac{\Theta_1 \omega_1^2}{2} = \frac{\Theta_1 \dot{\varphi}^2}{2}</math> - | + | <math>T_1 = \frac{\underline{\omega}_1 \cdot \underline{\underline{\Theta}}_1 \cdot \underline{\omega}_1}{2} = \frac{\Theta_1 \omega_1^2}{2} = \frac{\Theta_1 \dot{\varphi}^2}{2}</math> - Kinetic energy of first rod; Where |
| − | <math>\qquad \Theta_1 = \frac{m_1 a^2}{3}</math> - | + | <math>\qquad \Theta_1 = \frac{m_1 a^2}{3}</math> - Inertia torque of first rod<br> |
| − | <math>\Pi_1 = m_1 g \left( \frac{a}{2} - \frac{a}{2} \cos \varphi \right)</math> - | + | <math>\Pi_1 = m_1 g \left( \frac{a}{2} - \frac{a}{2} \cos \varphi \right)</math> - Potential energy of first rod<br> |
| − | <math>T_2 = \frac{\underline{\omega}_2 \cdot \underline{\underline{\Theta}}_2 \cdot \underline{\omega}_2}{2} + \frac{m_2 \vartheta_c^2}{2}</math> - | + | <math>T_2 = \frac{\underline{\omega}_2 \cdot \underline{\underline{\Theta}}_2 \cdot \underline{\omega}_2}{2} + \frac{m_2 \vartheta_c^2}{2}</math> - Kinetic energy of second rod<br> |
<math>\underline{\omega}_2 = ?</math><br><br> | <math>\underline{\omega}_2 = ?</math><br><br> | ||
| − | ''' | + | '''Finding second rod's angular velocity vector:''' <br> |
| − | + | For calculating <math>\underline{\omega}_2</math> we will find rotation tensors of both rods<br> | |
<math>\underline{\underline{P}}_1(\varphi,\underline{k}) = \underline{k}\underline{k} + (\underline{\underline{E}} - \underline{k}\underline{k})cos(\varphi) + \underline{k} \times \underline{\underline{E}}sin(\varphi)</math><br> | <math>\underline{\underline{P}}_1(\varphi,\underline{k}) = \underline{k}\underline{k} + (\underline{\underline{E}} - \underline{k}\underline{k})cos(\varphi) + \underline{k} \times \underline{\underline{E}}sin(\varphi)</math><br> | ||
<math>\underline{\underline{P}}_2(\psi,\underline{e}) = \underline{e}\underline{e} + (\underline{\underline{E}} - \underline{e}\underline{e})cos(\psi) + \underline{e} \times \underline{\underline{E}}sin(\psi)</math><br> | <math>\underline{\underline{P}}_2(\psi,\underline{e}) = \underline{e}\underline{e} + (\underline{\underline{E}} - \underline{e}\underline{e})cos(\psi) + \underline{e} \times \underline{\underline{E}}sin(\psi)</math><br> | ||
| − | + | Where:<br> | |
| − | <math>\underline{e} = \underline{\underline {P}}_1 \cdot \underline{e}_0</math> - | + | <math>\underline{e} = \underline{\underline {P}}_1 \cdot \underline{e}_0</math> - second rod's ongoing rotation axis<br> |
| − | <math>\underline{e}_0 = \cos(\alpha) \underline{k} + \sin(\alpha) \underline{i}</math> - | + | <math>\underline{e}_0 = \cos(\alpha) \underline{k} + \sin(\alpha) \underline{i}</math> - second rod's initial rotation axis<br><br> |
| − | <math>\underline{\underline{P}} = \underline{\underline{P}}_2 \cdot \underline{\underline{P}}_1</math> - | + | <math>\underline{\underline{P}} = \underline{\underline{P}}_2 \cdot \underline{\underline{P}}_1</math> - full rotation tensor for second rod<br><br> |
| − | + | But:<br> | |
<math> \underline{\underline{P}} = \underline{\underline{P}}_2 \cdot \underline{\underline{P}}_1 = \underline{\underline{P}}(\psi,\underline{e}) \cdot \underline{\underline{P}}_1 = \underline{\underline{P}}_1 \cdot \underline{\underline{P}}(\psi,\underline{e_0})\cdot \underline{\underline{P}}^T_1 \cdot \underline{\underline{P}}_1 = \underline{\underline{P}}_1 \cdot \underline{\underline{P}}(\psi,\underline{e_0})</math><br> | <math> \underline{\underline{P}} = \underline{\underline{P}}_2 \cdot \underline{\underline{P}}_1 = \underline{\underline{P}}(\psi,\underline{e}) \cdot \underline{\underline{P}}_1 = \underline{\underline{P}}_1 \cdot \underline{\underline{P}}(\psi,\underline{e_0})\cdot \underline{\underline{P}}^T_1 \cdot \underline{\underline{P}}_1 = \underline{\underline{P}}_1 \cdot \underline{\underline{P}}(\psi,\underline{e_0})</math><br> | ||
| − | + | Now using the angular velocity addition formula we get:<br> | |
<math>\underline{\omega}_2 = \underline{\omega}_1 + \underline{\underline{P}}_1 \cdot \underline{\tilde{\omega}}_2; \qquad \underline{\tilde{\omega}}_2 = \dot{\psi}\underline{e_0}</math><br> | <math>\underline{\omega}_2 = \underline{\omega}_1 + \underline{\underline{P}}_1 \cdot \underline{\tilde{\omega}}_2; \qquad \underline{\tilde{\omega}}_2 = \dot{\psi}\underline{e_0}</math><br> | ||
| − | + | So we got the equation:<br> | |
<math>\underline{\omega}_2 = \dot{\varphi} \underline{k} + \dot{\psi}\underline{e}</math><br><br> | <math>\underline{\omega}_2 = \dot{\varphi} \underline{k} + \dot{\psi}\underline{e}</math><br><br> | ||
| − | ''' | + | '''Finding second rod's center of mass velocity'''<br> |
<math>\underline{\vartheta}_c = \frac{1}{2}\underline{\omega}_2 \times \underline{b} + \dot{\varphi}\underline{k}\times \underline{a} ; \qquad \underline{a} = \underline{\underline{P}}_1 \cdot a\underline{j} ; \qquad \underline{b} = \underline{\underline{P}}_1 \cdot \underline{\underline{P}}(\psi,\underline{e_0}) \cdot b\underline{j}</math> | <math>\underline{\vartheta}_c = \frac{1}{2}\underline{\omega}_2 \times \underline{b} + \dot{\varphi}\underline{k}\times \underline{a} ; \qquad \underline{a} = \underline{\underline{P}}_1 \cdot a\underline{j} ; \qquad \underline{b} = \underline{\underline{P}}_1 \cdot \underline{\underline{P}}(\psi,\underline{e_0}) \cdot b\underline{j}</math> | ||
<br><br> | <br><br> | ||
| − | ''' | + | '''Finding second rod's kinetic energy'''<br> |
| − | + | Second rod's inertia tensor:<br> | |
<math>\underline{\underline{\Theta}}_2 = \frac{ml^2}{12}\left(\underline{\underline{E}} - \underline{\tilde{e}\tilde{e}} \right) ;\qquad \underline{\tilde{e}} = \underline{\underline{P}}_1 \cdot \underline{\underline{P}}(\psi,\underline{e_0}) \cdot \underline{j}</math><br><br> | <math>\underline{\underline{\Theta}}_2 = \frac{ml^2}{12}\left(\underline{\underline{E}} - \underline{\tilde{e}\tilde{e}} \right) ;\qquad \underline{\tilde{e}} = \underline{\underline{P}}_1 \cdot \underline{\underline{P}}(\psi,\underline{e_0}) \cdot \underline{j}</math><br><br> | ||
| − | + | Now we found all expressions required for second rod's kinetic energy formula:<br> | |
<math>T_2 = \frac{\underline{\omega}_2 \cdot \underline{\underline{\Theta}}_2 \cdot \underline{\omega}_2}{2} + \frac{m_2 \vartheta_c^2}{2}</math> | <math>T_2 = \frac{\underline{\omega}_2 \cdot \underline{\underline{\Theta}}_2 \cdot \underline{\omega}_2}{2} + \frac{m_2 \vartheta_c^2}{2}</math> | ||
<br><br> | <br><br> | ||
| − | ''' | + | '''Finding second rod's potential energy'''<br> |
| − | <math>\Pi_2 = mg(a+b - \underline{r}_c \cdot \underline{j}); \qquad \underline{r}_c = \underline{a} + \frac{1}{2}\underline{b}</math> - | + | <math>\Pi_2 = mg(a+b - \underline{r}_c \cdot \underline{j}); \qquad \underline{r}_c = \underline{a} + \frac{1}{2}\underline{b}</math> - radius-vector of second rod's center of mass<br><br> |
| − | ''' | + | '''Finding the motion equation'''<br> |
| − | + | We need to differentiate the equations for potential and kinetic energy, the way Lagrange equation requires and use the result in it. As the result we going to get the system of two differential equations which itself is equation of motion.<br> | |
| − | + | We notice that using this method we can get the motion equation also for big angles, it can be linearized assuming that angles <math>\varphi,\psi</math> are small and dropping terms of second order.<br> | |
| − | == | + | == Using this method for special case == |
| − | + | We'll check mentionad method for special case when <math>\alpha = 0</math><br> | |
| − | + | In this case problem becomes 2D.<br> | |
| − | ''' | + | '''Finding rotation tensors'''<br> |
<math>\underline{\underline{P}}_1(\varphi,\underline{k}) = \underline{k}\underline{k} + (\underline{\underline{E}} - \underline{k}\underline{k})cos(\varphi) + \underline{k} \times \underline{\underline{E}}sin(\varphi)</math><br><br> | <math>\underline{\underline{P}}_1(\varphi,\underline{k}) = \underline{k}\underline{k} + (\underline{\underline{E}} - \underline{k}\underline{k})cos(\varphi) + \underline{k} \times \underline{\underline{E}}sin(\varphi)</math><br><br> | ||
<math>\underline{e}_0 = \cos(\alpha) \underline{k} + \sin(\alpha) \underline{i} = \underline{k}</math><br> | <math>\underline{e}_0 = \cos(\alpha) \underline{k} + \sin(\alpha) \underline{i} = \underline{k}</math><br> | ||
| Строка 83: | Строка 84: | ||
<math>\underline{\underline{P}}_2(\psi,\underline{e})= \underline{\underline{P}}_2(\psi,\underline{k}) = \underline{k}\underline{k} + (\underline{\underline{E}} - \underline{k}\underline{k})cos(\psi) + \underline{k} \times \underline{\underline{E}}sin(\psi)</math><br><br> | <math>\underline{\underline{P}}_2(\psi,\underline{e})= \underline{\underline{P}}_2(\psi,\underline{k}) = \underline{k}\underline{k} + (\underline{\underline{E}} - \underline{k}\underline{k})cos(\psi) + \underline{k} \times \underline{\underline{E}}sin(\psi)</math><br><br> | ||
| − | ''' | + | '''Finding second rod's angular vielocity'''<br> |
<math>\underline{\omega}_2 = (\dot{\varphi}+\dot{\psi})\underline{k}</math><br><br> | <math>\underline{\omega}_2 = (\dot{\varphi}+\dot{\psi})\underline{k}</math><br><br> | ||
| − | ''' | + | '''Finding second rod's center of mass velocity'''<br> |
<math>\upsilon^2_c = \frac{1}{4} b^2 (\dot{\varphi}+\dot{\psi})^2 + ab\cos\psi(\dot{\varphi}+\dot{\psi})\dot{\varphi} + a^2\dot{\varphi}^2</math><br><br> | <math>\upsilon^2_c = \frac{1}{4} b^2 (\dot{\varphi}+\dot{\psi})^2 + ab\cos\psi(\dot{\varphi}+\dot{\psi})\dot{\varphi} + a^2\dot{\varphi}^2</math><br><br> | ||
| − | ''' | + | '''Finding second rod's kinetic energy'''<br> |
<math>T_2 = \frac{1}{2} \left( \frac{m_2 b^2}{3}(\dot{\varphi}+\dot{\psi})^2 + m_2 ab\cos\psi(\dot{\varphi}+\dot{\psi})\dot{\varphi} + m_2 a^2\dot{\varphi}^2 \right)</math><br><br> | <math>T_2 = \frac{1}{2} \left( \frac{m_2 b^2}{3}(\dot{\varphi}+\dot{\psi})^2 + m_2 ab\cos\psi(\dot{\varphi}+\dot{\psi})\dot{\varphi} + m_2 a^2\dot{\varphi}^2 \right)</math><br><br> | ||
| − | ''' | + | '''Finding second rod's potential energy'''<br> |
<math>\Pi_2 = m_2 g \left[ a \left(1-\cos\varphi \right) + \frac{b}{2}\left(2 + \sin\varphi\sin\psi - \cos\varphi\cos\psi \right) \right]</math><br><br> | <math>\Pi_2 = m_2 g \left[ a \left(1-\cos\varphi \right) + \frac{b}{2}\left(2 + \sin\varphi\sin\psi - \cos\varphi\cos\psi \right) \right]</math><br><br> | ||
| − | ''' | + | '''Finding first rod's kinetic and potential energy'''<br> |
<math>T_1 = \frac{1}{2}\frac{m_1 a^2}{3}\dot{\varphi}^2</math><br> | <math>T_1 = \frac{1}{2}\frac{m_1 a^2}{3}\dot{\varphi}^2</math><br> | ||
<math>\Pi_1 = m_1 g \left( \frac{a}{2} - \frac{a}{2} \cos \varphi \right)</math><br><br> | <math>\Pi_1 = m_1 g \left( \frac{a}{2} - \frac{a}{2} \cos \varphi \right)</math><br><br> | ||
| − | ''' | + | '''Finding equation of motion for this special case'''<br> |
| − | + | Let's write equations for system's kinetic and potential energy:<br> | |
<math>T = \frac{1}{2}\frac{m_1 a^2}{3}\dot{\varphi}^2 + \frac{1}{2} \left( \frac{m_2 b^2}{3}(\dot{\varphi}+\dot{\psi})^2 + m_2 ab\cos\psi(\dot{\varphi}+\dot{\psi})\dot{\varphi} + m_2 a^2\dot{\varphi}^2 \right)</math><br> | <math>T = \frac{1}{2}\frac{m_1 a^2}{3}\dot{\varphi}^2 + \frac{1}{2} \left( \frac{m_2 b^2}{3}(\dot{\varphi}+\dot{\psi})^2 + m_2 ab\cos\psi(\dot{\varphi}+\dot{\psi})\dot{\varphi} + m_2 a^2\dot{\varphi}^2 \right)</math><br> | ||
<math>\Pi = m_1 g \left( \frac{a}{2} - \frac{a}{2} \cos \varphi \right) + m_2 g \left[ a \left(1-\cos\varphi \right) + \frac{b}{2}\left(2 + \sin\varphi\sin\psi - \cos\varphi\cos\psi \right) \right]</math><br> | <math>\Pi = m_1 g \left( \frac{a}{2} - \frac{a}{2} \cos \varphi \right) + m_2 g \left[ a \left(1-\cos\varphi \right) + \frac{b}{2}\left(2 + \sin\varphi\sin\psi - \cos\varphi\cos\psi \right) \right]</math><br> | ||
| − | + | Now we differentiate both equations and linearise results assuming that <math>\varphi , \psi</math> are small and taking to account only infinitesimals of the first order. As the result we find equation of motion:<br> | |
<math> | <math> | ||
\begin{cases} | \begin{cases} | ||
| Строка 111: | Строка 112: | ||
</math> | </math> | ||
| − | == | + | == Discussing the results and conclusion == |
| − | + | The algorithm of solving the problem about double pendulum where both joints are cylindrical was described in this work. After that this method was used for special case of two-dimential problem. | |
| − | == | + | == Related links == |
*[http://en.wikipedia.org/wiki/Double_pendulum Double pendulum 2D Wiki]<br> | *[http://en.wikipedia.org/wiki/Double_pendulum Double pendulum 2D Wiki]<br> | ||
*[http://vuz.exponenta.ru/PDF/koleb2s2.html Двумерный случай двойного маятника] | *[http://vuz.exponenta.ru/PDF/koleb2s2.html Двумерный случай двойного маятника] | ||
| − | == | + | == See also == |
* [[Справка:Содержание|Справочная информация]] | * [[Справка:Содержание|Справочная информация]] | ||
* [[Курсовые проекты ТМ 20510 (2012)|Список курсовых проектов]] | * [[Курсовые проекты ТМ 20510 (2012)|Список курсовых проектов]] | ||
| − | * [[Кафедра "Теоретическая механика"]] | + | * [[Кафедра "Теоретическая механика"|Department for Theoretical Mechanics]] |
| − | * [[ | + | * [[Dzenushko Dainis]] |
[[Category: Студенческие проекты]] | [[Category: Студенческие проекты]] | ||
Текущая версия на 17:55, 17 сентября 2012
Содержание
Subject[править]
Specification of double pendulum oscillations
Task[править]
Rod is connected to the roof by cylindrical joint. The second rod is connected to the end of the first rod via cylindrical joint so that when both rods are vertical the angle between joint's axis equals to . Dissipative forces are not taken to account.
System parameters:
- Inertia tensor of first and second rods are equal. and respectively.
- length of rods are a and b, their masses and for first and second rods.
- Angle between rotation axis of joints equals to
- - angle between first rod and vertical direction
- - angle between axis of first and second rods that means the angle in second joint relative to vertical orientation of system.
Main task:
- find the equation of motion for this double pendulum
Solution[править]
Let's find the way of solving this problem: We are going to solve the problem by using the Lagrange equation:
- - Kinetic energy of system
- - Potential energy of system
- - Generalized coordinates
- - generalized velocities
- - generalized non-potential forces
Selecting generalized coordinates: for generalized coordinates we are going to use angles and
- In this problem we neglect non-potential interactions, so generalized non-potential forces equals to zero.
Calculating potential and kinetic energy of system: of first and second rods relatively.
- Potential energy of system
- Kinetic energy of system
- Kinetic energy of first rod; Where
- Inertia torque of first rod
- Potential energy of first rod
- Kinetic energy of second rod
Finding second rod's angular velocity vector:
For calculating we will find rotation tensors of both rods
Where:
- second rod's ongoing rotation axis
- second rod's initial rotation axis
- full rotation tensor for second rod
But:
Now using the angular velocity addition formula we get:
So we got the equation:
Finding second rod's center of mass velocity
Finding second rod's kinetic energy
Second rod's inertia tensor:
Now we found all expressions required for second rod's kinetic energy formula:
Finding second rod's potential energy
- radius-vector of second rod's center of mass
Finding the motion equation
We need to differentiate the equations for potential and kinetic energy, the way Lagrange equation requires and use the result in it. As the result we going to get the system of two differential equations which itself is equation of motion.
We notice that using this method we can get the motion equation also for big angles, it can be linearized assuming that angles are small and dropping terms of second order.
Using this method for special case[править]
We'll check mentionad method for special case when
In this case problem becomes 2D.
Finding rotation tensors
Finding second rod's angular vielocity
Finding second rod's center of mass velocity
Finding second rod's kinetic energy
Finding second rod's potential energy
Finding first rod's kinetic and potential energy
Finding equation of motion for this special case
Let's write equations for system's kinetic and potential energy:
Now we differentiate both equations and linearise results assuming that are small and taking to account only infinitesimals of the first order. As the result we find equation of motion:
Discussing the results and conclusion[править]
The algorithm of solving the problem about double pendulum where both joints are cylindrical was described in this work. After that this method was used for special case of two-dimential problem.