Численная оценка интеграла методом Монте-Карло. Антонов Илья. 6 курс — различия между версиями
| Строка 20: | Строка 20: | ||
==Результаты== | ==Результаты== | ||
Метод прямоугольников: | Метод прямоугольников: | ||
| − | [[File:graphMC_rand1.png]][[File:graphMC_rand2.png]] | + | [[File:graphMC_rand1.png|400px]][[File:graphMC_rand2.png|400px]] |
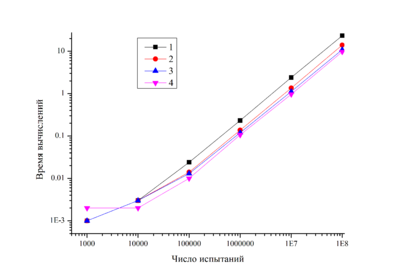
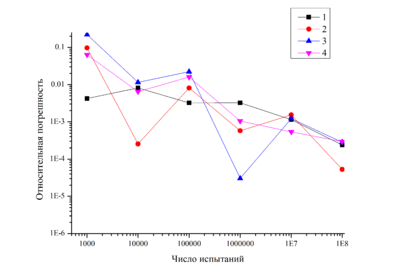
Метод Монте-Карло, srand(): | Метод Монте-Карло, srand(): | ||
| − | [[File:graphMC_rand3.png]][[File:graphMC_rand4.png]] | + | [[File:graphMC_rand3.png|400px]][[File:graphMC_rand4.png|400px]] |
Метод Монте-Карло, вихрь Мерсенна: | Метод Монте-Карло, вихрь Мерсенна: | ||
| − | [[File:graphMC_rand5.png]][[File:graphMC_rand6.png]] | + | [[File:graphMC_rand5.png|400px]][[File:graphMC_rand6.png|400px]] |
Версия 02:18, 27 января 2017
Цель работы
При применении технологии параллельных вычислениях в разных задачах зачастую наибольший интерес представляет характер убывания времени расчета при увеличении числа процессов на практике. Зная эту характеристику, например, для двух разных методов решения задачи, можно определить, какой из них будет предпочтительней при заданных условиях.
Основная цель данной работы — исследовать на распараллеливание простейший метод Монте-Карло численной оценки интеграла и сравнить его с классическим методом прямоугольников; по характеру убывания времени расчета и относительной погрешности определить, почему метод Монте-Карло для данной задачи используется лишь в качестве оценки; определить, как число процессов и выбор генератора случайных чисел сказывается на относительной погрешности при оценке интеграла методом Монте-Карло.
Описание исследования
Оценка интеграла методом Монте-Карло алгоритмически довольно проста. Подинтегральная функция геометрически заключается в простую фигуру, например, в прямоугольник (с заранее определенными минимальными и максимальными значениями функции в качестве высоты и пределами интегрирования в качестве ширины), по которому равномерно последовательно случайным образом разбрасываются точки. Испытание считается успешным, если точка попала под интегральную функцию. Значение интеграла оценивается как отношение числа успешных испытаний к общему числу испытаний, умноженному на площадь фигуры, в которую заключена подинтегральная функция. Кроме того, точность оценки будет зависеть равномерности распределения случайных точек по фигуре, то есть, в конечном счете, от генератора случайных чисел и генерируемого им равномерно-распределенного псевдослучайного числа. Предлагается сравнить стандартное РРПСЧ для C++ rand() и РРСПЧ из вихря Мерсенна (std::mt19937).
Такая задача довольно просто может быть распараллелена использованием своего генератора случайных чисел для каждого из процессов.
Для расчета был выбран следующий интеграл, заключенный в прямоугольник [(0,0);(10,1)]:
Решение задачи
Для сравнения методов было разработано консольное приложение на языке C++ с использованием технологии MPI для распараллеливания вычислений, которое позволяло рассчитать значение интеграла, определить время расчета и оценку относительной погрешности для:
- численного интегрирования функции методом прямоугольников;
- численной оценки интеграла методом Монте-Карло с использованием srand() в качестве РРПСЧ
- численной оценки интеграла методом Монте-Карло с использованием std::mt19937 generator() в качестве РРПСЧ
Результаты
Метод прямоугольников:
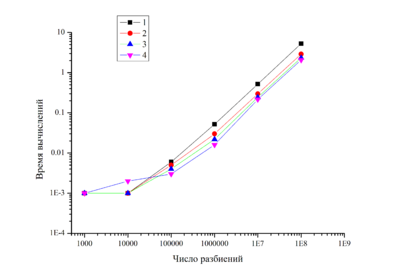
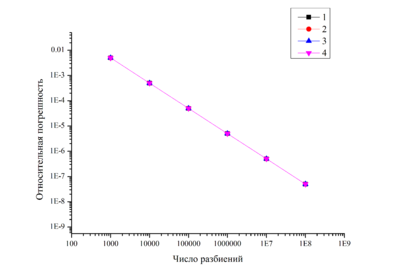Метод Монте-Карло, srand():
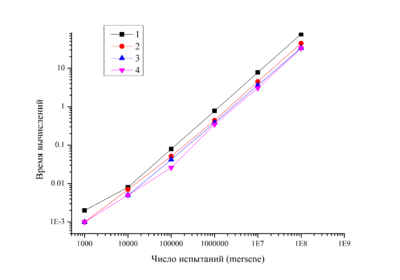
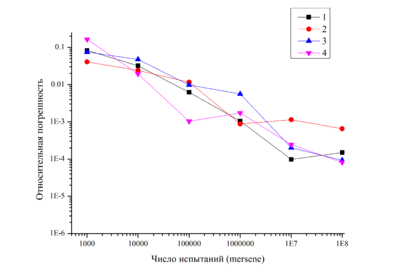Метод Монте-Карло, вихрь Мерсенна:
