Устойчивость протопланетного облака системы "Земля - Луна"

Проект выполняет Мурачёв Андрей, научный руководитель А.М.Кривцов.

Введение к первой модели

Рассматривается модель протопланетного облака, состоящего из пыли и газа, образовавшегося засчет испарения пылинок. Плотность вещества в протопланетном диске превышает [math]10^{-18} g/cm^3[/math], размеры частиц космической пыли составляют около 0,1 мкм . Газопылевой диск вокруг формирующейся звезды очень быстро "сплющивается" под действием сил гравитации и центробежной силы, направленных к наиболее плотной части диска в плоскости его вращения. Спустя несколько сотен тысяч лет диск имеет массу около 0,1 Масс Солнца, размеры от 0,2 до 50-70 а.е. и толщину около 0,001 диаметра. Размеры пылевых частиц увеличиваются в результате слипания до 10 мкм; их орбиты становятся почти круговыми. Акустические ударные волны, распространяющиеся в облаке при сжатии протозвездного сгустка вещества и возгорании молодой звезды, способствуют возникновению неоднородностей в диске.

Современные астрофизические модели химической конденсации предполагают, что исходный состав протопланетного облака был близок к составу межзвездной среды и Солнца: по массе до 75% водорода, до 25% гелия и менее 1% всех прочих элементов.

Температура в центральной плоскости протопланетного диска Солнечной системы уменьшалась с удалением от Солнца. Особенно сильно нагревалась ближайшая к звезде "горячая" зона облака: на расстоянии в 1 а.е. температура составляла 300-400 К.

Я пренебрегаю некоторыми важными деталями для облегчения расчёта и упрощения модели. Далее планируется их все,по возможности, учесть. В частности:

1. В протооблаке присутствует газ, помимо испарившегося с пылинок. Его влияние не рассматривается, так как считается, что он весь вытеснен солнечным излучением.

2. Пока непонятна степень оптической прозрачности облака, которая зависит от концентрации и сорта частиц. А именно она оказывает решающие влияние на испарение пылинок. Я считаю облако полностью прозрачным, что, естественно неправда.

4. Соударения между пылинками можно рассматривать, как абсолютно упругие. Хотя это тоже неправда.

Диффузия от точечного источника

Рассмотрим облако состоящие из небольших шариков, находящихся во взвешенном состоянии. Обозначим их частицами с концентрацией [math]w[/math], Теперь, пусть один какой-нибудь шарик начнёт испарятся-излучать равномерно частицы с концентрацией [math]n[/math], пренебрежительно малых размеров. Напишем уравнение диффузии:

[math] \frac{\partial n}{\partial t} - D\triangle n= \dot N\delta^3(r) [/math]

Итоги

Рассмотрим облако состоящие из небольших шариков, находящихся во взвешенном состоянии. Обозначим их частицами с концентрацией [math]w[/math], Теперь, пусть один какой-нибудь шарик начнёт испарятся-излучать равномерно частицы с концентрацией [math]n[/math], пренебрежительно малых размеров. Напишем уравнение диффузии:

[math] \frac{\partial n}{\partial t} - D\triangle n= \dot N\delta^3(r) [/math]

, где [math]n(r,t)[/math] -концентрация частиц второго сорта на расстоянии [math]r[/math] от излучающей частицы в некоторый момент времени [math]t[/math], [math] D =\frac 13 lv=\frac{v}{3(n\sigma_{n}+w\sigma_{w})}[/math] - коэффициент диффузии ([math]\sigma[/math]- сечение взаимодействия пылинок) (В выражении для [math]D[/math] можно спокойно пренебречь членом, вносящим нелинейность во все последующие рассуждения-[math]n\sigma_{n}[/math]. В данной модели газ пылинок довольно разрежен, и соударения между пылинками редки, но газ молекул в свою очередь должен быть ещё более разрежен и на собственную диффузию не оказывать какого-либо заметного влияния. Поэтому [math] D =\frac 13 lv=\frac 13\cdot\frac{v}{w\sigma_{w}}[/math] , [math] \dot N [/math]-количество частиц, оторвавшихся с единицы поверхности пылинки за единицу времени [[math]1\backslash[/math] сек].

Процесс в нашем случае стационарный, поэтому первое слагаемое в левой части равно 0. Плюс ко всему, избавляемся от дельта-функции.

[math] -D\frac{dn}{dr}\cdot 4\pi r^2=\dot N [/math]

Проинтегрируем по [math]r[/math] и найдём, что в устоявшемся процессе концентрация частиц сорта [math]n[/math] распределена по пространству таким вот образом:

[math] n(r)=\frac{\dot N}{4\pi rD},r\gt 0....................[1] [/math]

Случай дискообразного протопланетного облака

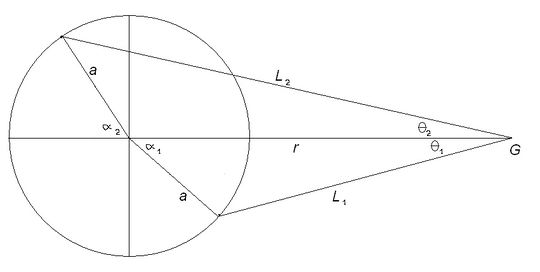
Выделим в облаке окружность с центром в точке (0,0) некоторого радиуса [math]r[/math]. Концентрация молекул газа, а следовательно и оказываемое ими давление в силу симметрии будет одинаковым. Найдём эту концентрацию: Сначала учтём вклад "внутренней" области выделенной окружности. Представим ещё одну сферу радиуса [math]a[/math], где [math]a\lt r[/math] и найдём влияние этой сферы на бесконечно маленький объём [math]G[/math] на сфере радиуса [math]r[/math]. Для этого, очевидно надо воспользоваться формулой [1], где [math]r[/math] пробегает по всем расстояниям (с каждой точки поверхности сферы до G).

[math]L[/math]-расстояние от точки [math]G[/math] до точек правой полуокружности.

[math]\alpha[/math]-угол между радиус-вектором [math]r[/math] и радиусом [math]a[/math]

Смотри рисунок internal.

internal

Легко сообразить для левой полуокружности:

[math]L_1=\sqrt{r^2+a^2-2ra\cos (\alpha+3\frac\pi2)}=\sqrt{r^2+a^2+2ra\cos \alpha}[/math]

и

[math]L_2=\sqrt{r^2+a^2-2ra\cos (\frac \pi2 +\alpha) }=\sqrt{r^2+a^2-2ra\cos (\alpha) }[/math][math]Вставьте сюда формулу[/math]

для правой.

Интегрирование по [math]L[/math] сводится к интегрированию по [math]\alpha[/math] от 0 до [math]\frac \pi 2[/math] для "верхнего левого" и "нижнего правого" сектора. А потом результат удваивается.

[math]n(r)_{internal}=2\int_0^r da \left( \int_0^{\frac \pi 2 } d\alpha \frac{\dot N\cdot n(a)^*}{4\pi D\sqrt{r^2+a^2-2ra\cos \alpha}}+ \int_0^{\frac \pi 2 } d\alpha \frac{\dot N\cdot n(a)^*}{4\pi D\sqrt{r^2+a^2+2ra\cos \alpha}}\right)[/math]

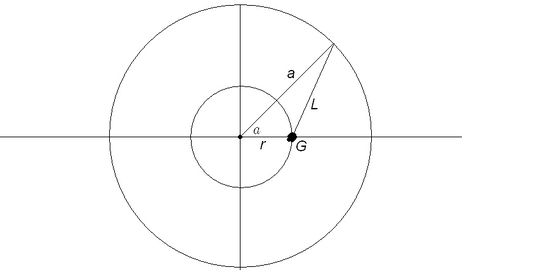
Теперь можно оценить вклад внешних слоёв на наш выделенный объём G . Смотри рисунок external. Можно заметить, что тут всё то же самое, что и в предыдущем примере, лишь точка [math]G[/math] <<переехала>> с одного конца отрезка на другой, а [math]a[/math] и [math]r[/math] поменялись местами. Поэтому повторяя предыдущие рассуждения, можно записать

external

[math]n(r)_{internal}=2\int_r^R da \left( \int_0^{\frac \pi 2 } d\alpha \frac{\dot N\cdot n(a)^*}{4\pi D\sqrt{r^2+a^2-2ra\cos \alpha}}+ \int_0^{\frac \pi 2 } d\alpha \frac{\dot N\cdot n(a)^*}{4\pi D\sqrt{r^2+a^2+2ra\cos \alpha}}\right)[/math]

Тогда влияние вклад в концентрацию от испарений всего облака будет

[math]n(r)=n(r)_{external}+n(r)_{internal}=[/math]

[math]2\int_0^R da \left( \int_0^{\frac \pi 2 } d\alpha \frac{\dot N\cdot n(a)^*}{4\pi D\sqrt{r^2+a^2-2ra\cos \alpha}}+ \int_0^{\frac \pi 2 } d\alpha \frac{\dot N\cdot n(a)^*}{4\pi D\sqrt{r^2+a^2+2ra\cos \alpha}}\right)[/math]

concentration

Значение концентрации пылинок

[math]w(a)=\sqrt{1-\frac{a^2}{R^2}}[/math]

Задача свелась к вычислению данных интегралов.

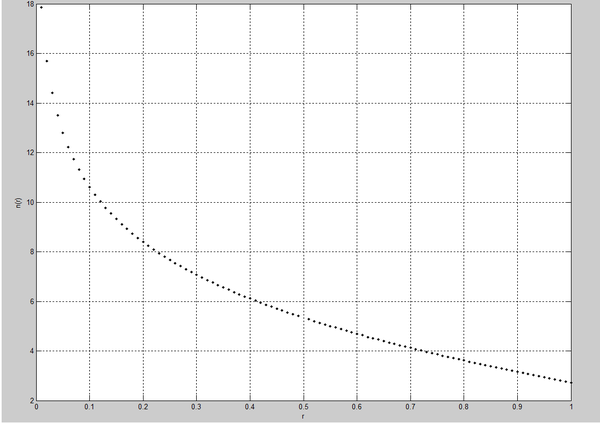
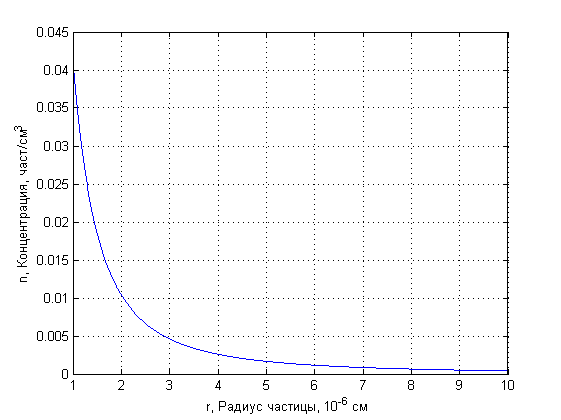
Но этот интеграл не берётся в элементарных функциях. Поэтому он был вычислен численно. На рисунке concentration, изображен результат численного интегрирования. Здесь [math]R=1[/math], и константа перед интегралом тоже взята за 1 (Точный вид этой константы зависит от константы диффузии [math]D[/math]). Что удивительно, при [math]r=R[/math], значение интеграла не равно нулю. Это можно объяснить тем, что у реального протопланетного диска нет чёткой границы.

Уравнение равновесия.

Для нашего облака сила гравитационного "самопритяжения", должна быть уравновешенна некими другими силами. Очевидно это будет сила давления газа и центробежная сила вращения облака.

[math]{\bf F_{grav}=F_c+F_{press}}[/math]

[math]\frac{Gm(r)}{r^2}=\frac{v^2}{r}+\frac{dP}{dr}\cdot\frac{1}{w(r)}[/math]

Второе слагаемое правой части самое важное в данном контексте. Выражение для давления состоит из двух частей: Давление газового облака (напомню, именно оно должно давать основной вклад в массу) и давления испарений. Газ, в силу разреженности можно считать идеальным.

Где, [math]m(r)[/math]-масса протопланетного диска радиуса [math]r[/math]

Испарение пылинок в вакуум

Интенсивность испарения [[math]g/cm^2\cdot sek[/math]] определяется формулой Ленгмюра.

[math] \nu=11,69 p^* \sqrt{\frac{\mu}{T}} [/math] , где

[math]p^*[/math]-давление насыщенного пара данного вещества, Па.

[math]\mu[/math]-молекулярная масса вещества

[math]T[/math]-Температура облака, K.

Эта формула выведена для абсолютного вакуума, поэтому реальная скорость испарения в космическом пространстве будет меньше расчётной.

[math] \dot m =4\pi r^3 \nu =\gt \left(\frac{4}{3}\pi r^3 \rho \right)'=4\nu\pi r^3 =\gt \dot r = \frac{\nu}{\rho} [/math]

Отсюда "время жизни" [math]t_l=\frac{r \rho}{\nu}[/math], для льдинок диаметром 10 мкм эта величина ровна [math] 4.4 \cdot 10^{-5}[/math] сек.

Можно сделать отсюда нижнюю оценку для диаметра частиц. На самом деле "время жизни" пылинки [math]t_l[/math] должно быть больше времени свободного пробега [math]\tau[/math] этой пылинки. Это очень грубо, но для первых оценок вполне достаточно.

[math]\tau=\frac{\sqrt{2}}{8\pi} \frac{1}{ w \cdot d^2v}[/math] ,

где

[math]v[/math]- средняя скорость пылинок,

[math]d[/math] -диаметр пылинок.

Сравнивая эту формулу с выражением для "времени жизни" пылинки находим

[math]d^3\gt \frac{\sqrt{2}}{4\pi} \frac{\nu}{\rho n_1 v}[/math]

Давление насыщенного пара воды при [math]30^o C[/math] равно 4.2455 кПа.

Плотность льда равна 0,917 г/см³

Молекулярная масса воды равна 18 а. е. м.

Теперь остался главный вопрос о концентрации и скорости пылинок.

Вторая модель

(Черновые тезисы)

• Вопрос на который должна дать данная часть работы, можно сформулировать так: "Как изменится концентрация испарившихся молекул после прохождения через испаряющейся участок пылевого облака"

• Работа состояла из двух частей: Компьютерного 2D моделирования эксперимента и поиска аналитического решения.

• Эксперимент и аналитика дали хорошее совпадение результатов. Рисунки представлены ниже.

рис. 1. Прохождение "лучей" через неиспаряющееся облако.

рис. 2. Прохождение "лучей" в испаряющемся облаке.

рис. 3. Сумма двух вкладов.

рис. 4. Эта зависимость от расстояния при заданной концентрации.

Об аналитическом решении

Чтобы найти закон распространения радиационного излучения в облаке, воспользуемся простой моделью. Некоторый объём пространства представим в виде цилиндра с основанием [math]H[/math] и длиной [math]L[/math]. В этом цилиндре находятся частицы-сферы радиуса r.

Пусть, перпендикулярно основанию в цилиндр, по прямым траекториям входят N лучей радиационного излучения. Рассматривается случай, когда нет никаких отражений, т.е. луч упавший на сферу, ей тотчас поглощается.

Наша задача ответить на вопрос: сколько в среднем лучей достигнет противоположной стенки цилиндра?

Эта задача равносильна следующей: На некоторой поверхности [math]H[/math] нанесена в случайном месте точка. На поверхность набрасываются случайным образом [math]N[/math] окружностей площадью [math]S[/math] [math](S=\pi r^2)[/math]. Какова вероятность того, что точка останется непокрытой? Будем решать её.

Ответ легко получить из закона распределения Пуассона.

Для начала-формальное определение:

Пусть производится [math]n[/math] независимых испытаний. Если число испытаний [math]N[/math] достаточно велико, а вероятность появления события [math]А[/math] в каждом испытании мало ([math]p\in(0,1)[/math]), то вероятность появления события [math]А[/math] [math]k[/math] раз находится следующим образом. Сделаем важное допущение – произведение [math]np[/math] сохраняет постоянное значение: [math]np=\lambda[/math] Практически это допущение означает, что среднее число появления события в различных сериях испытаний (при разном [math]N[/math]) остается неизменным.

[math]P_n(k)=\frac{\lambda^k e^{-\lambda}}{k!}[/math]

Очевидно, что вероятность того, что точка покроется одной окружностью есть отношение площадей окружности и поверхности:[math]p=\frac{S}{H}[/math]. Тогда для [math]N[/math] окружностей эта вероятность: [math]\lambda=\frac{n\cdot S}{H}[/math]

Вероятность, что точка будет покрыта ровна [math]к[/math] окружностями из [math]n[/math] даёт формула Пуассона.

Нас интересует случай, когда [math]k=0[/math]. Случай когда точка не покрылась ни одной окружностью, т.е. случай, когда луч прошёл через цилиндр со сферами ни встретив ни одну на своём пути.

Подставляя [math]k=0[/math], в формулу Пуассона, находим [math]P_n(0)=e^{-\lambda}[/math]. Тогда из [math]N[/math] лучей в среднем пройдёт

[math]N_{ex}=N\cdot e^{-\lambda}=N\cdot e^{-\frac{n\cdot S}{H}}[/math] .......................................(1)

лучей.

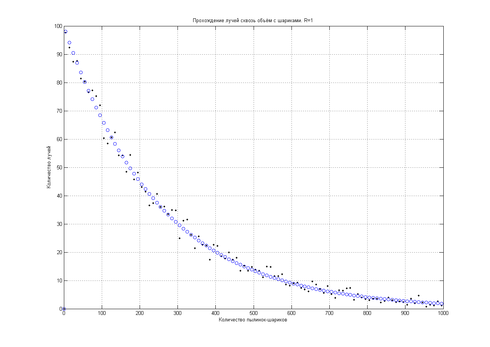
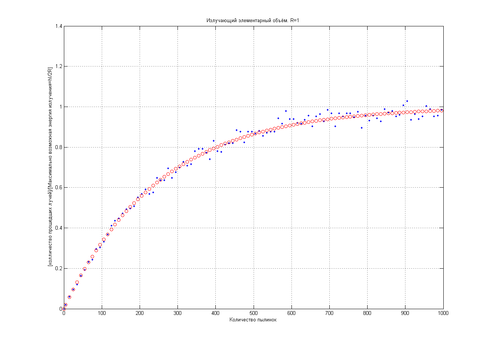
Зависимость числа пройдённых лучей от концентрации в некотором объёме проиллюстрирована на рис. 1.

Теперь рассмотрим другую ситуацию.

Тот же объём и те же шарики. Но теперь радиационное излучение не падает на стенки цилиндра, а каждый шарик излучает в произвольном направлении луч. Спрашивается, сколько лучей пройдёт через основание цилиндра?

Сперва откажемся от требования произвольности направления излучения. Пусть луч выходит из центра шарика в направлении основания [math]H[/math]. Тогда для луча с шарика, находящегося на расстоянии [math]x[/math] от поверхности [math]H[/math], вероятность прохожднения через оставшейся объём одного луча есть

[math]N_j^{*}=e^{-\frac{n\cdot S\cdot x}{H\cdot L}}[/math].................................................................(2)

где [math]L[/math] это длинна цилиндра. Соответственно, если излучается [math]I[/math] лучей, то последнее выражение надо умножить на [math]I[/math].

Чтобы найти количество лучей вышедших из бесконечно тонкого объёма, параллельного [math]H[/math], и находящегося на расстоянии [math]x[/math], очевидно необходимо (2) умножить на [math]N/L[/math].

Для всех шариков в цилиндре:

[math]N_j=\frac{N\cdot I}{L}\int_{0}^{L} e^{-\frac{n\cdot S\cdot x}{H\cdot L}} dx =\frac{N\cdot I\cdot H}{n\cdot S}(1-e^{-\frac{n\cdot S}{H}} ) [/math].................................................(3)

Для того, чтобы учесть случайность направления луча, следует выражение (3) умножить на вероятность того, что луч попадёт в угловой сегмент с основанием [math]H[/math] и вершиной в центре частички.

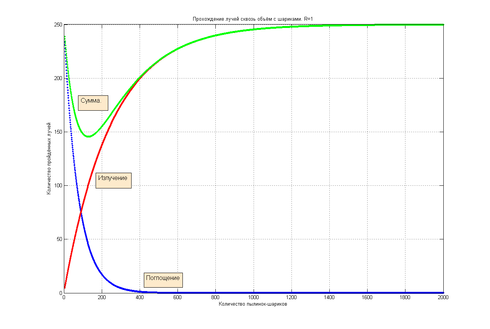
Иллюстрацию этого закона можно видеть на рис. 3.

К сожалению, это выражение столь сложно, что интеграл "руками" не берётся. Поэтому проводилось только численное интегрирование.

[math]N_j=\int_0^l I\cdot n\cdot \left(2\cdot arctg(\frac{H}{x})\cdot H- x\cdot ln(1+\frac{H^2}{x^2})\right)\cdot exp(-n \cdot S \cdot x)[/math]......................................................(4)

, где [math]n[/math]-концентрация пылинок

[math]I[/math]- интенсивность испарения.

Оценки для устойчивости

Две частицы в протопланетном облаке взаимодействуют по средством гравитации и радиационного излучения, вызванного испарением частицы.

Сила гравитационного притяжения:

[math]F_g=G\frac{m^2}{r^2}=\frac{16 \pi^2 G\rho_p^2 r_p^6}{9 r^2}[/math].......................................(5)

Сила радиационного отталкивания в пустом пространстве есть

[math]F_v=\frac{N m_0 v r_p^2}{4 r^2} [/math]

При выводе этой формулы, столкновения между молекулами не учитывалось.

Если ввести

[math]Nm_0=4\pi r_p^2 \nu[/math]- количество массы испаряющееся с пылинки за единицу времени (величина независящая от размеров частицы), то предыдущая формула перепишется, как

[math]F_v=\frac{\pi \nu v r_p^4 }{4 r^2} [/math]..................................................................(6)

[math]k=\frac{f_v}{f_g}= \frac {9\nu v}{16\pi G r_p^2 \rho^2} [/math]

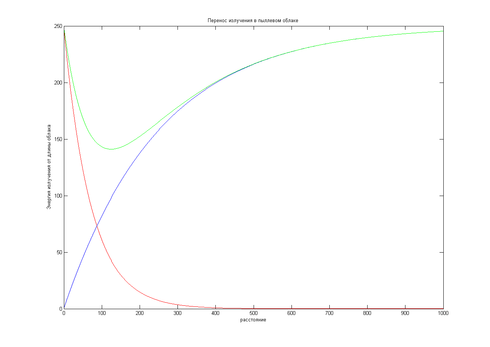
При [math]k=1[/math], силы газодинамического отталкивания, полностью уравновешивают силу гравитационного притяжения (рис.5).

Для пространства заполненного другими частицами, создающими экранирующий эффект

[math]F_v=\frac{\pi \nu v r_p^4 exp(-n \cdot \pi r_p^2 \cdot r)}{r^2}[/math]..................................................................(7)

,Где [math]n[/math]-концентрация пылинок в рассматриваемом объёме.

При равенстве этих сил облако будет находиться в равновесии.

Между тем, понятно, что при любой, отличной от нуля концентрации и при любом, отличном от нуля размере пылинок будет присутствовать эффект экранирования. Взаимодействие далёких частиц будут всё более отходить от закона обратных квадратов.

Будем считать, что облако может находиться в равновесии, если отношение сил радиационного отталкивания и гравитационного притяжения меньше одного процента.

[math]k=\frac{F_v}{F_g}\le 0.99\%[/math] ....................................................(8)

[math]k=\frac{F_v}{F_g}=\frac{9\pi\nu v \cdot exp(-n \cdot \pi r_p^2 \cdot r)}{16 \pi^2 G r_p^2\rho^2 }[/math]

Среднею скорость примем равной среднему значению модуля скорости идеального газа:

[math]v=\sqrt{\frac{8RT}{\pi}}[/math]

Радиус облака равен среднему расстоянию между Землёй и Луной ( [math]L=3,84\cdot 10^{10}[/math] см ).

Пусть на расстоянии [math]2L[/math] выполняется условие (8).

Если принять [math]\lt math\gt k=\frac{F_v}{F_g}=\frac{9\pi\nu v }{16 \pi^2 G r_p^2\rho^2 } =1 [/math], то значит </math>, то [math] exp(-n \cdot \pi r_p^2 \cdot 2L)=0.99[/math]

Следовательно:

[math] n \cdot \pi r_p^2 \cdot 2L=-ln(0.99)=0.01 =\gt n \cdot \pi r_p^2=2.6*10^{-13} [/math]

Тогда построим зависимость концентрации от площади, при условии сохранения постоянным их произведения.

рис.5

Ссылки по теме

• Снимки зарождающихся планетных систем в туманности Ориона, полученные космическим телескопом Хаббл
• А. Мурачев. Некоторые замечания по модели образования системы Земля-Луна в результате ротационного коллапса газопылевого облака (черновые наброски). Скачать презентацию, pptx: 2741 kb