Распределение тепла в одномерном кристалле
Выполнил: Цветков Д. В.
Научный руководитель: Кривцов А. М.
Скачать:
Содержание
- 1 Введение
- 2 Сравнительный анализ решений задач теплопроводности для бесконечного слоя, находящегося под воздействием ультракороткого лазерного импульса
- 3 Задача о переходе энергии механических колебаний в тепло для нелинейного одномерного кристалла
- 4 Заключение
- 5 Список использованной литературы
Введение[править]
На данный момент одной из наиболее активно развивающихся областей современной механики является механика наноструктур. Благодаря нанотехнологиям появляется возможность получать практически идеальные, бездефектные материалы. Требуется уметь предугадывать свойства и поведение таких материалов. Благодаря развитию компьютерных технологий имеется возможность моделировать достаточно крупные фрагменты материала, и исследовать их поведение на требуемом отрезке времени.
Также важной темой является исследование Парадокса возврата, следующего из теоремы Пуанкаре о возвращении, по отношению к достаточно коротким одномерным кристаллам. Суть Парадокса возврата в противоречии между возможностью молекул вещества любой динамической системы, сохраняющей механическую энергию, вернуться в окрестность своего первоначального положения, и такими необратимыми процессами, как теплопроводность или диффузия.
Пример: сосуд, разделенный перегородкой (рис.1а). В левой части сосуда содержится небольшое количество молекул газа, правая часть сосуда пуста. Убираем перегородку (рис.1б). Постепенно молекулы газа занимают все пространство сосуда (рис.1в). Но, так как молекул очень мало, через некоторое время они снова одновременно окажутся в левой части сосуда (рис.1г).
- Сосуд с небольшим количеством молекул газа
Если в начальный момент времени в левой части сосуда будет больше молекул (рис.2а), то, после удаления перегородки (рис.2б) ждать возвращения системы в начальное состояние (когда все молекулы находятся в левой части сосуда) придется намного дольше. В этом и состоит разгадка Парадокса возврата --- для достаточно большого тела вероятность обращения таких процессов, как теплопроводность, настолько мала, что время на ожидание такого возврата много больше времени существования вселенной.
- Сосуд с большим количеством молекул газа
Важно исследовать граничное время, в которое возврат системы становится практически невозможен.
В этой связи в данной работе рассматривается процесс преобразования механической энергии нелинейного одномерного стержня в тепловую и обратно с течением времени. Исследуется влияние флуктуаций скоростей на скорость преобразования энергии.
Сравнительный анализ решений задач теплопроводности для бесконечного слоя, находящегося под воздействием ультракороткого лазерного импульса[править]
Метод исследования[править]
Рассматривается задача одномерного теплоизолированного кристалла, нагретого ультракоротким лазерным импульсом. Производится сравнение следующих решений:
- стохастическое решение --- задача динамики кристалла, температура кристалла задается с помощью случайных скоростей
- численное решение дифференциального уравнения, полученного в [1]:
- аналитическое решение, полученное в [2]:
где --- интенсивность входящего пучка света, --- коэффициент поглощения света.
Для численного расчета и сравнения задач написано специальное программное обеспечение на языке MATLAB.
Постановка стохастической задачи[править]
Рассмотрим одномерный кристалл: цепочку одинаковых частиц массы , соединенных одинаковыми линейными пружинами с жесткостью :
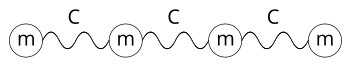
Уравнения динамики кристалла имеют вид:
где --- перемещение -й частицы; --- индекс, принимающий произвольные целые значения, --- жесткость связи между частицами, --- масса частицы.
Температура в кристалле определяется как дисперсия скоростей частиц. Скорости частиц задаются с помощью генератора случайных чисел.
Начальные условия[править]
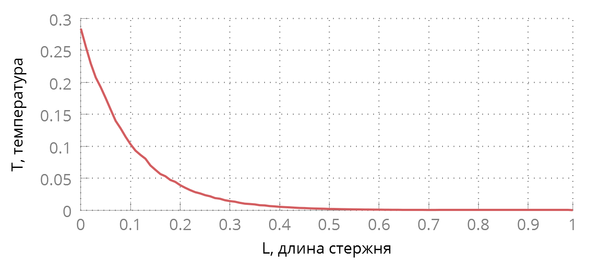
Требуемое распределение температуры по координате в кристалле на начальный момент времени описывается формулой:
где --- интенсивность входящего пучка света, --- коэффициент поглощения света, --- постоянная Больцмана. Согласно закону Бугера [3], данные начальные условия можно интерпретировать как результат воздействия на кристалл ультракороткого лазерного импульса.
Задание начальных скоростей[править]
Температура в кристалле задается с помощью скоростей. Воспользуемся определением кинетической температуры для одномерного случая:
где --- постоянная Больцмана, --- оператор усреднения по координате. Выразим :
Для того, чтобы получить требуемое распределение, будем задавать скорости с помощью случайного числа в диапазоне .
Посчитаем, чему равно :
Значит .
Заменим на , генерируемое с помощью :
Выразим :
При генерации скорости с помощью данной формулы, получается требуемое распределение температуры по координате:
Задание начальных перемещений[править]
Если задать нулевые начальные перемещения, то потенциальная энергия кристалла будет равна нулю, и с течением времени примерно половина кинетической энергии преобразуется в потенциальную [1]. Чтобы этого избежать, начальные перемещения задаются с помощью деформаций. Деформации задаются таким образом, чтобы кинетическая и потенциальная энергии кристалла в начальный момент времени были равны.
Сначала задаются случайных чисел, сумма которых равна нулю:
где --- количество частиц в цепочке. После рассчитывается параметр :
и кинетическая энергия :
Далее, с помощью отношения к находятся деформации:
Граничные условия[править]
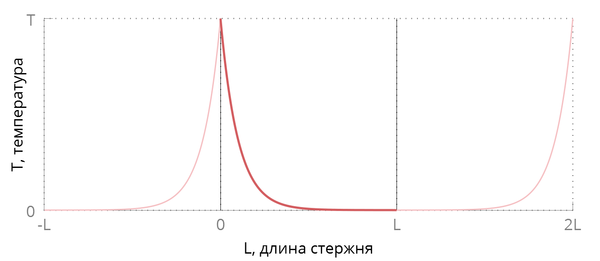
Граничные условия --- зеркальные. Это значит, что значения перемещения и скорости частицы на границе равны значениям перемещения и скорости соседней частицы:
где --- число частиц в цепочке.
При данных условиях энергия не убывает и не прибывает --- на границах стержня выполняется условие теплоизоляции.
Результаты[править]
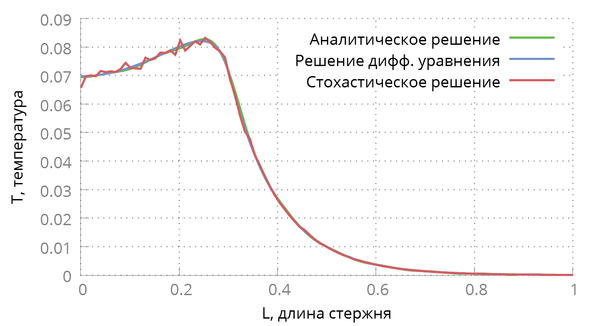
На рисунке аналитическое решение сравнивается со стохастическим решением и численным решением дифференциального уравнения. Численное решение получено для 125 реализаций цепочки из 10000 частиц. Легко видеть, что решения совпадают с точностью до малых тепловых осцилляций.
Задача о переходе энергии механических колебаний в тепло для нелинейного одномерного кристалла[править]
Постановка задачи[править]
Рассмотрим одномерный кристалл: цепочку одинаковых частиц массы , соединенных одинаковыми нелинейными пружинами с жесткостью . Уравнения динамики кристалла имеют вид:
где --- перемещение -й частицы; --- индекс, принимающий произвольные целые значения. Будем считать, что выполнены условия периодичности: , где --- число независимых частиц.
Рассматриваются два случая:
- Детерминированная задача --- при перемещения частиц равны нулю, а скорости распределены по синусоидальному закону.
- Стохастическая задача --- к скоростям в детерминированной задаче добавляются случайные флуктуации.
Детерминированная задача[править]
Начальные условия[править]
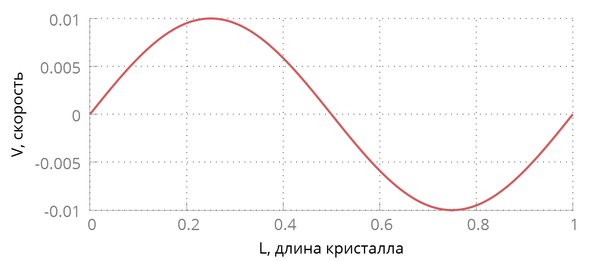
Начальные скорости в кристалле задаются следующим образом:
где --- амплитуда, --- длина кристалла, .
Начальные перемещения равны нулю по всей длине кристалла.
Метод определения формы кристалла в различные моменты времени[править]
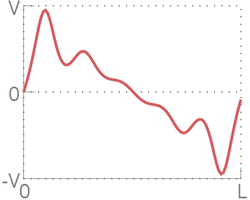
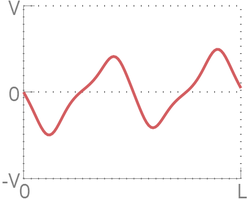
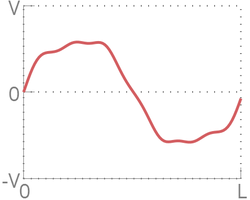
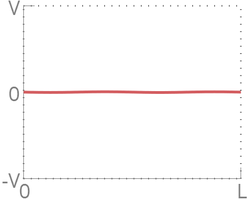
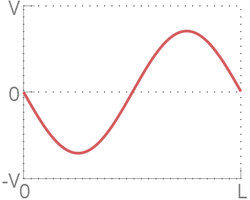
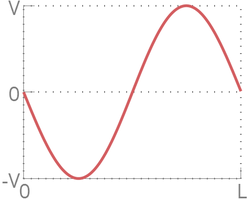
При малых в распределении скоростей по длине цепочки явно прослеживается форма синуса, однако, при возрастании цепочка теряет свою форму и движение частиц неотличимо от теплового. Это случается из за нелинейного взаимодействия между частицами. Однако, с течением времени цепочка вновь принимает форму синуса, искривленного тепловым движением.
- Трансформации синуса
Чтобы более точно определить, насколько форма цепочки близка к форме синуса, посчитаем параметр --- отношение полной механической энергии к начальной полной механической энергии по следующей формуле:
. Чем больше параметр , тем больше форма кристалла похожа на синус.
Анализ решения задачи на большом отрезке времени[править]
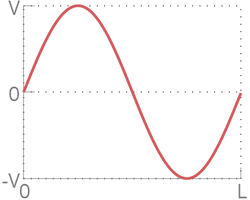
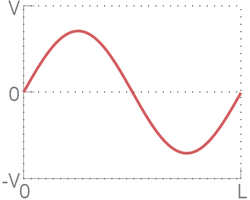
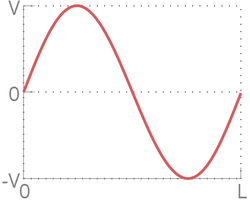
Время в данной главе измеряется в количестве осцилляций синуса. Под этим подразумевается время, за которое любая движущаяся со временем точка графика скорости кристалла совершит полное колебание. На рисунке ниже продемонстрирована одна осцилляция синуса.
- T --- период осцилляции синуса
Использованы следующие параметры системы: амплитуда , количество частиц ;
По графику ниже видно, что через некоторое время система возвращается к состоянию, близкому к начальному. Это означает, что распределение скоростей вновь приобретает форму синуса. Также видно, что система возвращается к начальному состоянию не на , а с некоторым отклонением.
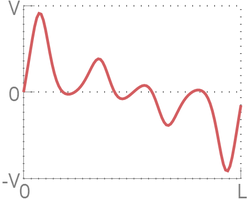
На рисунке ниже изображен тот же график, но на больший промежуток времени. По нему можно определить, в какой момент и насколько (относительно) распределение скоростей в цепочке было максимально похоже на начальное. Видно, что высота пика не снижается постоянно, а меняется по определенному закону.
Зависимость времени возвращения кристалла к начальному состоянию от количества частиц и амплитуды синуса[править]
При фиксированной амплитуде имеется линейная зависимость между количеством частиц в цепочке и временем, требуемым для возвращения синуса к начальному состоянию (время измеряется в периоде колебаний синуса).
Амплитуда .
Для того, чтобы глубже понять характер зависимости между временем, требуемым для возвращения кристалла к начальному состоянию, количеством частиц и амплитудой синуса, рассчитаны значения для разных амплитуд. Графики зависимостей представлены на рисунке ниже:
По рисунку видно, что при увеличении амплитуды синуса время, требуемое на возврат системы к начальному состоянию уменьшается.
Высота второго пика[править]
На рисунке ниже показана зависимость высоты второго пика функции от количества частиц в цепочке. Амплитуда . Под вторым пиком подразумевается второй по времени локальный максимум функции , который означает, что после преобразования механической энергии кристалла в тепловую, произошло обратное преобразование, и тепловая энергия кристалла в максимальной степени преобразовалась в механическую. В этот момент распределение скоростей в кристалле вновь приобретает форму синуса.
По графику можно предположить, что с увеличением количества частиц значение асимптотически стремится к нулю, но рассчитать его для большего затруднительно, т.к. время, требуемое на расчет такой системы, растет нелинейно с увеличением количества частиц в цепочке.
Стохастическая задача[править]
Заключение[править]
Рассчитан одномерный кристалл, нагретый с помощью ультракороткого лазерного импульса. Проведено сравнение трех решений:
- решения стохастической задачи, где одномерный кристалл представлен как цепочка частиц, для которых задается масса, жесткость и температура как дисперсия скоростей частиц.
- решения дифференциального уравнения, взятого из [1]
- аналитического решения из [2].
Полученное решение стохастической задачи совпадает с решением дифференциального уравнения и аналитическим решением с точностью до малых тепловых осцилляций.
Исследована задача о переходе механической энергии в тепловую и обратно в нелинейном одномерном кристалле. Заданная изначально механическая энергия в нелинейном одномерном кристалле постепенно переходит в тепловую. Если кристалл достаточно короткий, то через некоторое время происходит обратная трансформация энергии --- некоторая часть тепловой энергии переходит обратно в механическую.
Чем длиннее кристалл, тем дольше нужно ждать обратной трансформации энергии, и тем меньше тепловой энергии перейдет обратно в механическую.
Время , требуемое на то, чтобы тепловая энергия трансформировалась обратно в механическую, зависит от начальных условий. Если распределение скоростей в кристалле задано с помощью синусоиды, то обратно пропорционально амплитуде её колебаний.
Список использованной литературы[править]
- ↑ 1,0 1,1 1,2 Кривцов А.М. Колебания энергий в одномерном кристалле. --- Доклады Академии Наук, 2014, том 458, №3, с. 279-281.
- ↑ 2,0 2,1 Бабенков М.Б., Цветков Д.В. Распространие тепла в линейном одномерном кристалле. --- в печати.
- ↑ Путилов К.А. Курс физики. Том III. Оптика. Атомная физика. Ядерная физика. --- М.: ГИ ФМЛ, 1963, 636 с.


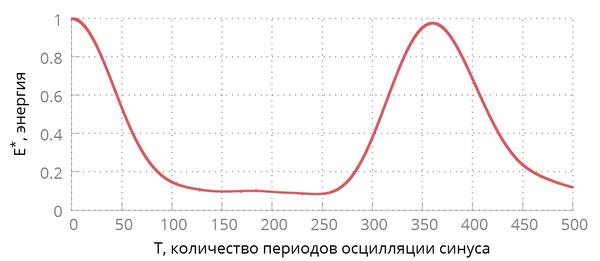
![Результаты, большое [math]T[/math]](http://mech.spbstu.ru/images/thumb/7/79/Tcvet_masters_Theme3_Temperature_long.png/600px-Tcvet_masters_Theme3_Temperature_long.png)
![[math]T(N)[/math] для различных значений амплитуды](http://mech.spbstu.ru/images/thumb/5/55/Tcvet_masters_Theme3_time_reverse%28N%2CA%29_6_lines.png/600px-Tcvet_masters_Theme3_time_reverse%28N%2CA%29_6_lines.png)
![Высота второго пика от [math]N[/math]](http://mech.spbstu.ru/images/thumb/1/16/Tcvet_masters_Theme3_second_peak_height.png/600px-Tcvet_masters_Theme3_second_peak_height.png)