Разработка электро-механических моделей углеродных нановискеров как детекторов масс — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
(→‎Дифференциальный резонатор)
 
(не показано 15 промежуточных версий 2 участников)
Строка 32: Строка 32:
 
==Задача о вискере, колеблющемся на игле==
 
==Задача о вискере, колеблющемся на игле==
 
Первая исследуемая конструкция представляет из себя одиночный прямой вискер, колеблющийся на игле. В ходе одного из экспериментов над такой системой было обнаружено, что существует две близкие собственные частоты этой системы с похожими формами колебаний.
 
Первая исследуемая конструкция представляет из себя одиночный прямой вискер, колеблющийся на игле. В ходе одного из экспериментов над такой системой было обнаружено, что существует две близкие собственные частоты этой системы с похожими формами колебаний.
−
[[File:Sameshapes.png|framed|left|Колебания одиночного вискера на игле]]
+
[[File:Sameshapes.png|thumb|400px|left|Колебания одиночного вискера на игле]]
−
 
 
−
Уравнения каждой из таких балок: <math>\rho F\frac{\partial^2 w}{\partial t^2}=-E J\frac{\partial^4 w}{\partial x^4} </math>
 
  
 +
Уравнения каждой из таких балок: <math> \rho F\frac{\partial^2 w}{\partial t^2}=-E J\frac{\partial^4 w}{\partial x^4} </math>. Это уравнения колебаний балки Бернулли-Эйлера.
 
Для построения приближённого решения задачи о двух балках используется метод, предложенный В.М.Фридманом, заключающемся в использовании спектральных свойств отдельных элементов системы. В соответствии с работой уравнения движения системы
 
Для построения приближённого решения задачи о двух балках используется метод, предложенный В.М.Фридманом, заключающемся в использовании спектральных свойств отдельных элементов системы. В соответствии с работой уравнения движения системы
 
балок могут быть для удобства записаны в операторном виде.
 
балок могут быть для удобства записаны в операторном виде.
Строка 42: Строка 41:
 
M
 
M
 
\end{array} \right) </math><math>\eta=\left( \begin{array}{cc} w\\ \theta \end{array} \right) </math>
 
\end{array} \right) </math><math>\eta=\left( \begin{array}{cc} w\\ \theta \end{array} \right) </math>
−
 
+
Так же вводятся <math>D</math> и <math>D^*</math> - дифференциальные операторы вида, а <math>R</math> и <math>B</math> - алгебраические операторы инерции и упругости: <math>D=\left( \begin{array}{cc}
−
<math>D=\left( \begin{array}{cc}
 
 
-\frac{\partial }{\partial x} & 0\\
 
-\frac{\partial }{\partial x} & 0\\
 
1 & -\frac{\partial }{\partial x}
 
1 & -\frac{\partial }{\partial x}
 
\end{array} \right) \qquad D^*=\left( \begin{array}{cc} \frac{\partial }{\partial x} & 1\\ 0 & \frac{\partial }{\partial x} \end{array} \right)</math>
 
\end{array} \right) \qquad D^*=\left( \begin{array}{cc} \frac{\partial }{\partial x} & 1\\ 0 & \frac{\partial }{\partial x} \end{array} \right)</math>
−
 
+
,<math>R=\left( \begin{array}{cc}
−
<math>R=\left( \begin{array}{cc}
 
 
\rho & 0\\
 
\rho & 0\\
 
0 & j
 
0 & j
 
\end{array} \right) \qquad B=\left( \begin{array}{cc} b & 0\\ 0 & \beta \end{array} \right)</math>
 
\end{array} \right) \qquad B=\left( \begin{array}{cc} b & 0\\ 0 & \beta \end{array} \right)</math>
 +
Важно заметить, что для <math>D</math> и <math>D^*</math> верно следующее соотношение, оно позволяет связать эти два дифференциальных оператора.
 +
<math>\int\limits_0^l D \xi \eta \,dx +\xi\eta\bigg|_{x=0}^{x=l} = \int\limits_0^l \xi D^* \eta \,dx</math>
 +
Тогда уравнения колебаний балок примут следующий вид:<math>\begin{array}{l}
 +
D \xi - \lambda^2 R \eta = 0
 +
\\
 +
D^* \eta - B \xi = 0
 +
\end{array}</math>
 +
 +
Так же необходимо учесть разложение решений на две составляющие:<math> \xi = \widetilde{\xi} + \bar{\xi} \qquad \eta = \widetilde{\eta} + \bar{\eta}</math>.
 +
Здесь составляющая с волной обозначает разложение по всем собственным формам каждой из балок, а слагаемое с чертой отвечает за сопряжение вискера с иглой. Решение с волной это сумма собственных форм колебаний с некоторыми коэффициентами:<math> \widetilde{\xi} = \sum_{i=1}^\infty \alpha_i \widetilde{\xi}_i \qquad \widetilde{\eta} = \sum_{i=1}^\infty \beta_i \widetilde{\eta}_i  </math>
 +
 +
А решение с чертой представимо в виде:<math>\bar{\eta}=b_1 \left( \begin{array}{cc}
 +
1\\
 +
0
 +
\end{array} \right) + b_2 \left( \begin{array}{cc}
 +
x\\
 +
-1
 +
\end{array} \right) \qquad \bar{\xi}=a_1 \left( \begin{array}{cc}
 +
1\\
 +
0
 +
\end{array} \right) + a_2 \left( \begin{array}{cc}
 +
x\\
 +
1
 +
\end{array} \right)</math>
 +
В ходе дальнейшего решения, находится зависимость коэффициентов разложения по собственным формам от коэффициентов в решении с чертой. Далее с помощью уравнений колебаний балок в операторном виде составляется система уравнений относительно коэффициентов части решения с чертой. В этой зависимости будет присутствовать <math> \lambda</math> - собственная частота всей системы. В результате получается уравнение относительно ее. Весь ход решения здесь не приведен, в силу его громоздкости, но его можно посмотреть в тексте дипломной работы.
 +
  
−
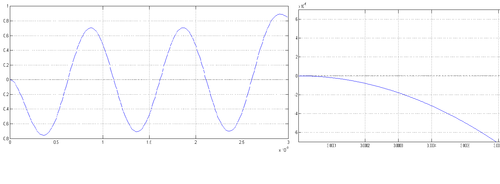
<math>\int\limits_0^l D \xi \eta \,dx +\xi\eta\bigg|_{x=0}^{x=l} = \int\limits_0^l \xi D^* \eta \,dx</math>
+
Предполагается,что объяснение этого эксперимента заключается в том, что нельзя рассматривать вискер, как консольную балку на неподвижном основании, необходимо учитывать колебания иглы, хотя она много превышает размерами вискер. Более того, можно предположить, что игла колеблется со своей высокой частотой, соответствующей одной из многоузловых форм колебаний. Поэтому во всем решении была учтена высокая частота балки и первая частота вискера.  То есть разложение по собственным формам колебаний проводилось до слагаемого, равного по номеру количеству учтенных собственных частот.
 +
[[File:Blabaa.png|thumbnail|500px|Форма колебаний иглы и вискера в системе]]
 +
Результатом такого метода решения стал набор собственных чисел всей системы игла-вискер. Колебания системы при полученных частотах имеют вид, изображенный на рисунке.
 +
 
 +
==Дифференциальный резонатор==
 +
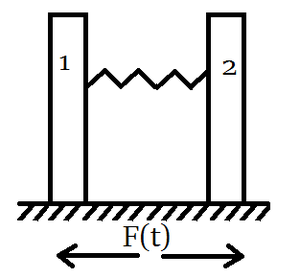
Под дифференциальным резонатором из углеродных вискеров понимается система, состоящая из двух параллельно расположенных вискеров, соединённых между собой упругой перемычкой и закреплённых на жёстком основании. Свободные колебания системы с двумя степенями свободы и близкими собственными частотами имеют вид биений. Период огибающей сильно зависит даже от малых изменений упругих и инерционных свойств системы, что может позволить повысить точность измерения малых добавленных масс.
 +
В качестве модели, для исследования такого резонатора были взяты две балки Бернулли-Эйлера, с заделкой на нижнем конце и свободные с верхнего. При этом упругая перемычка моделируется, как пружина, соединяющая два вискера. При частотах колебаний, близких к резонансным уравнения будут иметь следующий вид: <math>\begin{array}{c}
 +
m \ddot{x_1} + b \dot{x_1} +c x_1 + c \varepsilon (x_1 - x_2) = F(t)
 +
\\
 +
m \ddot{x_2} + b \dot{x_2} +c x_2 + c \varepsilon (x_2 - x_1) = F(t)
 +
\end{array}</math> В правой части стоит вынуждающая сила колебаний, которая выражает колебания подложки под вискерами.
 +
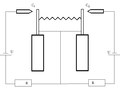
[[File:2whiskera.png|thumb|300px|left|Колебания одиночного вискера на игле]]
 +
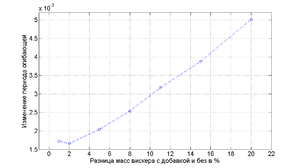
Для измерения масс в приведенных выше уравнениях необходимо взять разные массы вискеров. Одна из них считается равной елинице, а вторая отличается от неё на несколько процентов. Тогда при увеличении разницы между массами вискеров, частота огибающей будет возрастать.
 +
<gallery mode=""traditional"">
 +
File:2-2.png|Колебания одного из вискеров при разнице масс 3%
 +
File:3-2.png|Колебания одного из вискеров при разнице масс 5%
 +
File:6-2.png|Колебания одного из вискеров при разнице масс 15%
 +
</gallery>
 +
[[File:Graph11.png|thumb|300px|right|Зависимость частоты огибающей от приложенной массы]]
 +
Зависимость частоты огибающей от массы, прикрепленной к одному из вискеров является практически линейной, если добавочная масса более 2%. То есть возможно производить градуировку нановесов на основе 2-3 измерений. Это значительно упрощает производство таких приборов.
 +
 
 +
== Емкостные датчики колебаний==
 +
В работе рассмотрены три вида емкостных датчиков колебаний.
 +
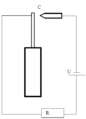
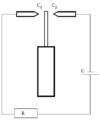
* Первый самый простой датчик представляет из себя электрическую цепь, включающую в себя конденсатор с переменным сопротивлением. Одной из обкладок конденсатора является вискер. Колебания вискера вызывают колебания напряжения в цепи. Проблемой данного датчика является нелинейность выходного сигнала.
 +
<gallery mode=""traditional"">
 +
File:Condensator.png|Устройство емкостного датчика колебаний одиночного вискера
 +
File:2condens.png|Устройство емкостного датчика колебаний двойного вискера
 +
File:Lineinii.png|Устройство улучшенного емкостного датчика колебаний одиночного вискера
 +
</gallery>
 +
Размерные уравнения колебаний такого вискера и соответствующего ему напряжения выглядят следующим образом:<math> \begin{array}{l}
 +
U-R i-u_c=0
 +
\\
 +
m \ddot{x}+b \dot{x} + cx - \frac{C u_c ^2}{d}= F(t)
 +
\end{array} </math>. Первое уравнение показывает распределение напряжений в цепи. То есть напряжение от источника частично тратится на сопротивление цепи, а частично на перезарядку конденсатора. Второе уравнение это уравнение механических колебаний вискера с демпфером, но с учетом действующей на него электрической силы.
 +
В результате численного решения этих уравнений получаются результаты, представленные на рисунке. Видно, что вискер имеет гармоническую форму колебаний, а напряжения нет. Но период и частота совпадают.
 +
*Второй датчик рассчитан на измерение колебаний двойного вискера и на детектирование масс. Он состоит из двух вискеров, связанных между собой упругой перемычкой, каждый из которых подключен к своему конденсатору.  Уравнение колебаний будут выглядеть следующим образом:  <math> \begin{array}{l}
 +
m \ddot{x_1} + b \ddot{x_1} - \frac{C_1 u_1^2}{d}+\epsilon c (x_1 - x_2) = F(t)
 +
\\
 +
m \ddot{x_2} + b \ddot{x_2} - \frac{C_2 u_2^2}{d}+\epsilon c (x_2 - x_1) = F(t)
 +
\\
 +
U-R i_1-u_1c=0
 +
\\
 +
U-R i_2-u_2c=0
 +
\end{array}</math>
 +
Эти уравнения отличаются от предыдущих тем, что в механической части добавилось слагаемое, отвечающее за упругую связь между вискерами. В результате интегрирования видно, что график напряжения полностью повторяет график механических колебаний, главное, что возможно точно измерить период огибающей биений, то есть померить массу с помощью напряжения.
  
−
== Модель нановесов ==
+
*Последний датчик предназначен для точного измерения колебаний одиночного вискера. Его особенность заключается в том, что один и тот же вискер выступает в роли обкладки для двух конденсаторов. Тогда выходной сигнал каждого из напряжений будет нелинейным, как и в первом случае, однако, если в качестве результата рассматривать разность напряжений на конденсаторах, то выходной сигнал получается гармоническим, точно совпадающим по частоте с колебаниями вискера, это дает возможность измерять частоту колебаний одиночного вискера с большой точностью. Уравнения колебаний такого датчика выглядят следующим образом: <math>m \ddot{x} + b \ddot{x} - \frac{C_1 u_1^2}{d}- \frac{C_2 u_2^2}{d} = F(t)
−
Исследуемые весы сделаны из углеродных наноструктур, называемых одиночными вискерами. Это углеродная балка очень маленьких размеров. На нее падает частица с некоторой скоростью, в результате чего вискер начинает колебаться. Исследовав колебания вискера, можно будет определить массу объекта, упавшего на   вискер. Для этого была построена конечноэлементная модель вискера с точечной массой на правом конце и заделкой на левом. Проведен расчет собственных частот и форм колебаний, а так же найдено аналитическое решение:<math>f = \sqrt\frac{3E(\frac{d}{2})^4}{16\pi (0.227*m_1+M)l^3}</math>, где <math>f </math> -собственная частота колебаний системы.
+
\\
−
[[File:Scalesreal.png|framed|right|Нановесы]]
+
U-R i_1-u_1c=0
−
Было проведено сравнение результатов, полученных аналитически и методом конечных элементов.
+
\\
−
[[File:Theorpract.png|framed|left|Сравнение зависимости собственной частоты от массы взвешиваемого объекта в зависимости от метода решения.]]
+
U-R i_2-u_2c=0</math>
  
−
== Конечноэлементное моделирование сложных структур.==
+
<gallery mode=""traditional"">
−
Для рассмотрения колебаний сложных структур, были созданы их конечноэлементные мо- дели и проведен расчет собственных и вынужденных колебаний.При создании моделей, бы- ли использованы размеры реальных наноконструкций, но увеличенные в 106 раз, так как в программном пакете ANSYS Workbench не предусмотрена работа с наноразмерами, однако понятно, что собственные формы не изменятся, а значения частот уменьшатся в 106 раз, не меняя при этом свое мантиссы. Некоторые из получившихся результатов представлены ниже.
+
File:UstCondens.png|Колебания вискера и напряжения в простейшем датчике
 +
File:2n.png|Колебания вискера и напряжения в датчике двойного вискера
 +
File:Lineinii2.png|Колебания вискера и напряжений в двойном датчике
 +
File:Lineinii3.png|Колебания вискера и разности напряжений в двойном датчике
 +
</gallery>
  
 
==Выводы==
 
==Выводы==
−
В данной работе проведено исследование продольных и поперечных колебаний вискера на игле с помощью представления этой системы в виде механической системы с двумя степенями свободы. Для продольных и поперечных колебаний были найдены аналитически уравнения движения и созданы интерактивные модели.Эти модели позволяют анализировать текущее движение системы в зависимости от параметров вискера и иглы.
+
В работе было рассмотрен и объяснён эксперимент с одиночным вискером, колеблющемся
−
В дальнейшем к данной части работы будет добавлена модель с постоянным гармоническим воздействием на иглу, что позволит исследовать колебания, более приближенные к реальным и рассмотреть случай динамического гашения колебаний вискера.
+
на игле; исследована и смоделирована система, состоящая из двух вискеров, соединённых
−
Так же была рассмотрена модель нановесов для случая падения массы точно на конец вискера.  
+
упругим элементом; рассмотрены различные емкостные датчики колебаний.
−
Были смоделированы сложные конструкции из вискеров, такие как вилка, скальпель и камертон. При моделировании этих конструкции мы получили два набора собственных частот (два спектра), так как модели трехмерные. Полезны собственные частоты и формы только в плоскости самой конструкции, так как при реальных экспериментах колебания происходят именно в этих плоскостях. Найдены только первые две собственные частоты каждого спектра, это объясняется тем, что чем ниже порядок частоты, тем проще попасть в нее при реальных экспериментах. Практически невозможно попасть в резонанс с третей и выше собственными частотами.
+
 
−
Для модели вискера на игле представлены только две собственные формы, так как эта модель осесимметрична и ее спектры и собственные формы, соответствующие частотам этих двух спектров совпадают,но располагаются в разных плоскостях. В дальнейшем, планируется решить полностью задачу нановесов, составив систему уравнений, для нахождения собственных частот; исследовать более сложные конструкции, например трехмерные; создать интерактивную модель динамического гасителя колебаний.
+
Решение задачи об одиночном вискере, колеблющемся на игле, объясняет природу явления, зафиксированного в эксперименте, а так же предлагает метод приближённого решения
−
Продолжение данного исследования необходимо, так как направление экспериментального создания вискеров развивается очень быстро. За последний год были построены и исследова- ны гораздо более сложные конструкции и найдены новые пути их применения. Но каждый эксперимент трудоемок, сложен и требует как финансовых, так и ресурсных затрат. В будущем планируется предсказывать результаты эксперементов с целью сокращения их числа и достижения максимальной эффективности работы специалистов-экспериментаторов.
+
подобных проблем. Метод решения (использования операторного подхода и разложения Галёркина) не увеличивает размерность задачи при увеличении количества искомых собственных частот, боле того, он учитывает особенности системы и позволяет находить только нужные собственные частоты и формы. Применить использованный подход можно так же и ко многим другим
−
[[File:2tuning.png|Колебания нанокамертона]]
+
задачам.
−
[[File:2xyFork.png|Клебания нановилки]]
+
 
 +
Следующая задача, изученная в этой работе, это система из двух вискеров, связанных
 +
между собой упругой перемычкой, так называемый дифференциальный резонатор. Изученный
 +
дифференциальный резонатор имеет аналоги, которые обладают как своими преимуществами, так и недостатками, но основной принцип работы остаётся одинаковым, что подтверждается схожестью результатов исследования вискерного резонатора с его аналогами. Одним из
 +
преимуществ дифференциального резонатора, рассмотренного в этой работе, является способ
 +
его раскачки, гарантирующий получение достаточной для наблюдений амплитуды колебаний.
 +
Главным направлением применения такой конструкции является измерение масс наночатсиц.
 +
 
 +
Последним этапом проведённого исследования было изучение емкостных датчиков, с помощью которых можно производить измерения колебаний нановискеров. Изучено три вида датчиков. Все они основаны на использовании вискера в качестве одной из обкладок конденсатора, подключенного в электрическую цепь. Такие устройства позволяют измерять напряжение в сети, вместо измерения амплитуды или частоты колебаний самого вискера.  
 +
 
 +
Все проведённое исследование основано на экспериментах с нановискерами и направлено на их улучшение и объяснение. Понимание процессов, происходящих при натурном исследовании нанообъектов позволяет упростить и усовершенствовать эксперименты, а также
 +
сократить количество неудачных, что ведет к значительной экономии денежных средств,
 +
материалов и времени учёных-эксперементаторов.
 +
 
  
 
==Список литературы==
 
==Список литературы==
−
* Z.L.Wang, P.Poncharal, W.A. de Heer. Measuring physical and mechanical properties of individual carbon nanotubes by in situ TEM. J. Phys. Chem. Solids, 2000, 61(7), pp.1025- 1030
+
*Левичев В.В. Электронные и фотонные устройства: принцип работы, технологии изготов-
−
* Dynamik der Baukonstruktionen, Christian Petersen 2000 1st edition,722 [3] И.М.Бабаков. Теория колебаний.1968,3
+
ления. //Учебник, учебное пособие, Год: 2015]
−
* Я.С.Гринберг, Ю.А.Пашкин, Е.В.Ильичев. Наномеханические резонаторы.2012.
+
* Я.С.Гринберг, Ю.А.Пашкин, Е.В.Ильичев. Наномеханические резонаторы.//Успехи фи-
−
* Mai Duc Dai, Chang-Wan Kim, Kilho Eom. Nonlinear vibration of graphene resonators and their applications in sensitive mass detection. Nanoscale Research Letters 2012  7:499
+
зических наук. Т.182. №4. 2012.
−
* Новопашенный Г.Н. Электронные измерительные приборы. 1966. 268
+
* Левичев В.В., Жуков М.В., Мухин И.С., Денисюк А.И., Голубок А.О. Об устойчивости
 +
работы сканирующего силового микроскопа с нановискером на вершине зонда.// Журнал
 +
технической физики, 2013, том 83, вып. 7
 +
* Голубок А.О., Ковров А.В., Левичев В.В., Мухин И.С., Приходько О.А. Формирова-
 +
ние одиночных нановискеров на вершинах зондов сканирующего зондового микроскопа.
 +
Научно-технический вестник Санкт-Петербургского государственного университета ин-
 +
формационных технологий, механики и оптики. 2009. № 4(62). С. 82-87. [Тип: Статья,
 +
Год: 2009]
 +
* Жилин П. А. Прикладная механика. Теория тонких упругих стержней: Учеб. пособие.
 +
СПб.: Изд-во Политехн. ун-та, 2007. 101 с.
 +
* Фридман В. М. Теория упругих колебаний: уравнения и методы / В. М. Фридман ; Рос.
 +
акад. наук, Ин-т проблем машиноведения. - Санкт-Петербург : Наука, 2014. - 253, [1] с.;
 +
16 усл. печ. л. - Библиогр.: с. 248-250 (61 назв.). - 500 экз. - ISBN 978-5-02-038375-3 (в пер.)
 +
*Галёркин Б. Г. Стержни и пластинки. Ряды в некоторых вопросах упругого равновесия
 +
стержней и пластинок. // Вестник инженеров. — 1915. — Т. 1. — С. 897—908.
 +
* Штукин Л.В., Беринский И.Е., Индейцев Д.А., Морозов Н.Ф., Скубов Д.Ю. Электроме-
 +
ханические модели нанорезонаторов. //Физическая мезомеханика 19 1 2016г
 +
* И.Е. Бринский, Д.И. Индейцев, Н.Ф. Морозов, Д.Ю. Скубов, Л.В. Штукин. Дифферен-
 +
циальный резонатор как детектор массы. // Механика твердого тела. №2 2015.
 +
* Д.И. Индейцев, О.С. Лобода, Н.Ф. Морозов, Д.Ю. Скубов, Л.В. Штукин. Автоколеба-
 +
тельный режим нанорезонатора. //Физическая мезомеханика 19 5 2016г с. 23-28
 +
*Н. Ф. Морозов, И.Е. Бринский, Д.И. Индейцев, О.В. Привалова, Д.Ю. Скубов, Л.В. Шту-
 +
кин. Срыв колебаний графенового резонатора, как способ определения его спектральных
 +
характеристик. ДОКЛАДЫ АКАДЕМИИ НАУК, 2014, том 456, № 5, с. 1–5
 +
41

Текущая версия на 16:11, 11 июня 2017

МАГИСТЕРСКАЯ РАБОТА
Автор работы: Ванюшкина Валентина
Научный руководитель: Л.В. Штукин

Введение[править]

Наноструктуры - объекты, созданные человеком и имеющие малые размеры (от нескольких нанометров до сотен микрометров). Эта область науки открывает много новых и интересных возможностей для экспериментов и теоретических расчётов. Наноструктуры могут быть очень полезны для медицины, механики, инженерии и биологии: могут быть ис- пользованы для разрезания клеток, взвешивания объектов на нано- и микро- уровнях, а так же для построения более сложных структур. Одной из технологий для создания наноструктур является напыление аморфного углерода на металлическую иглу. Целью данной работы является подробное исследование двух углеродных наноструктур Одна из них это прямолинейный одиночный вискер. Длина такого вискера порядка несколь- ких микрометров, а максимальная толщина всего лишь несколько десятков нанометров. Вис- кер выращен на вершине металлической иглы и закреплен на ней. Вторая исследуемая кон- струкция, это система из двух вискеров, связанных между собой упругой перемычкой. Пере- мычка так же создана из углерода путём напыления. Задачи данной работы заключаются в исследовании и описании одного из экспериментов с одиночным вискером на игле с помощью применения приближённого метода решения; опи- сание модели и изучение дифференциального резонатора из нановискеров для возможного применения его в качестве детектора масс; изучения одного из способов точного измерения колебаний нановискера и дифференциального резонатора с помощью различных емкостных датчиков.

  • Одиночный вискер

  • Двойной вискер


Задача о вискере, колеблющемся на игле[править]

Первая исследуемая конструкция представляет из себя одиночный прямой вискер, колеблющийся на игле. В ходе одного из экспериментов над такой системой было обнаружено, что существует две близкие собственные частоты этой системы с похожими формами колебаний.

Колебания одиночного вискера на игле

Уравнения каждой из таких балок: [math] \rho F\frac{\partial^2 w}{\partial t^2}=-E J\frac{\partial^4 w}{\partial x^4} [/math]. Это уравнения колебаний балки Бернулли-Эйлера. Для построения приближённого решения задачи о двух балках используется метод, предложенный В.М.Фридманом, заключающемся в использовании спектральных свойств отдельных элементов системы. В соответствии с работой уравнения движения системы балок могут быть для удобства записаны в операторном виде. [math]\xi=\left( \begin{array}{cc} Q\\ M \end{array} \right) [/math][math]\eta=\left( \begin{array}{cc} w\\ \theta \end{array} \right) [/math] Так же вводятся [math]D[/math] и [math]D^*[/math] - дифференциальные операторы вида, а [math]R[/math] и [math]B[/math] - алгебраические операторы инерции и упругости: [math]D=\left( \begin{array}{cc} -\frac{\partial }{\partial x} & 0\\ 1 & -\frac{\partial }{\partial x} \end{array} \right) \qquad D^*=\left( \begin{array}{cc} \frac{\partial }{\partial x} & 1\\ 0 & \frac{\partial }{\partial x} \end{array} \right)[/math] ,[math]R=\left( \begin{array}{cc} \rho & 0\\ 0 & j \end{array} \right) \qquad B=\left( \begin{array}{cc} b & 0\\ 0 & \beta \end{array} \right)[/math] Важно заметить, что для [math]D[/math] и [math]D^*[/math] верно следующее соотношение, оно позволяет связать эти два дифференциальных оператора. [math]\int\limits_0^l D \xi \eta \,dx +\xi\eta\bigg|_{x=0}^{x=l} = \int\limits_0^l \xi D^* \eta \,dx[/math] Тогда уравнения колебаний балок примут следующий вид:[math]\begin{array}{l} D \xi - \lambda^2 R \eta = 0 \\ D^* \eta - B \xi = 0 \end{array}[/math]

Так же необходимо учесть разложение решений на две составляющие:[math] \xi = \widetilde{\xi} + \bar{\xi} \qquad \eta = \widetilde{\eta} + \bar{\eta}[/math]. Здесь составляющая с волной обозначает разложение по всем собственным формам каждой из балок, а слагаемое с чертой отвечает за сопряжение вискера с иглой. Решение с волной это сумма собственных форм колебаний с некоторыми коэффициентами:[math] \widetilde{\xi} = \sum_{i=1}^\infty \alpha_i \widetilde{\xi}_i \qquad \widetilde{\eta} = \sum_{i=1}^\infty \beta_i \widetilde{\eta}_i [/math]

А решение с чертой представимо в виде:[math]\bar{\eta}=b_1 \left( \begin{array}{cc} 1\\ 0 \end{array} \right) + b_2 \left( \begin{array}{cc} x\\ -1 \end{array} \right) \qquad \bar{\xi}=a_1 \left( \begin{array}{cc} 1\\ 0 \end{array} \right) + a_2 \left( \begin{array}{cc} x\\ 1 \end{array} \right)[/math] В ходе дальнейшего решения, находится зависимость коэффициентов разложения по собственным формам от коэффициентов в решении с чертой. Далее с помощью уравнений колебаний балок в операторном виде составляется система уравнений относительно коэффициентов части решения с чертой. В этой зависимости будет присутствовать [math] \lambda[/math] - собственная частота всей системы. В результате получается уравнение относительно ее. Весь ход решения здесь не приведен, в силу его громоздкости, но его можно посмотреть в тексте дипломной работы.


Предполагается,что объяснение этого эксперимента заключается в том, что нельзя рассматривать вискер, как консольную балку на неподвижном основании, необходимо учитывать колебания иглы, хотя она много превышает размерами вискер. Более того, можно предположить, что игла колеблется со своей высокой частотой, соответствующей одной из многоузловых форм колебаний. Поэтому во всем решении была учтена высокая частота балки и первая частота вискера. То есть разложение по собственным формам колебаний проводилось до слагаемого, равного по номеру количеству учтенных собственных частот.

Форма колебаний иглы и вискера в системе

Результатом такого метода решения стал набор собственных чисел всей системы игла-вискер. Колебания системы при полученных частотах имеют вид, изображенный на рисунке.

Дифференциальный резонатор[править]

Под дифференциальным резонатором из углеродных вискеров понимается система, состоящая из двух параллельно расположенных вискеров, соединённых между собой упругой перемычкой и закреплённых на жёстком основании. Свободные колебания системы с двумя степенями свободы и близкими собственными частотами имеют вид биений. Период огибающей сильно зависит даже от малых изменений упругих и инерционных свойств системы, что может позволить повысить точность измерения малых добавленных масс. В качестве модели, для исследования такого резонатора были взяты две балки Бернулли-Эйлера, с заделкой на нижнем конце и свободные с верхнего. При этом упругая перемычка моделируется, как пружина, соединяющая два вискера. При частотах колебаний, близких к резонансным уравнения будут иметь следующий вид: [math]\begin{array}{c} m \ddot{x_1} + b \dot{x_1} +c x_1 + c \varepsilon (x_1 - x_2) = F(t) \\ m \ddot{x_2} + b \dot{x_2} +c x_2 + c \varepsilon (x_2 - x_1) = F(t) \end{array}[/math] В правой части стоит вынуждающая сила колебаний, которая выражает колебания подложки под вискерами.

Колебания одиночного вискера на игле

Для измерения масс в приведенных выше уравнениях необходимо взять разные массы вискеров. Одна из них считается равной елинице, а вторая отличается от неё на несколько процентов. Тогда при увеличении разницы между массами вискеров, частота огибающей будет возрастать.

  • Колебания одного из вискеров при разнице масс 3%

  • Колебания одного из вискеров при разнице масс 5%

  • Колебания одного из вискеров при разнице масс 15%

Зависимость частоты огибающей от приложенной массы

Зависимость частоты огибающей от массы, прикрепленной к одному из вискеров является практически линейной, если добавочная масса более 2%. То есть возможно производить градуировку нановесов на основе 2-3 измерений. Это значительно упрощает производство таких приборов.

Емкостные датчики колебаний[править]

В работе рассмотрены три вида емкостных датчиков колебаний.

  • Первый самый простой датчик представляет из себя электрическую цепь, включающую в себя конденсатор с переменным сопротивлением. Одной из обкладок конденсатора является вискер. Колебания вискера вызывают колебания напряжения в цепи. Проблемой данного датчика является нелинейность выходного сигнала.

  • Устройство емкостного датчика колебаний одиночного вискера

  • Устройство емкостного датчика колебаний двойного вискера

  • Устройство улучшенного емкостного датчика колебаний одиночного вискера

Размерные уравнения колебаний такого вискера и соответствующего ему напряжения выглядят следующим образом:[math] \begin{array}{l} U-R i-u_c=0 \\ m \ddot{x}+b \dot{x} + cx - \frac{C u_c ^2}{d}= F(t) \end{array} [/math]. Первое уравнение показывает распределение напряжений в цепи. То есть напряжение от источника частично тратится на сопротивление цепи, а частично на перезарядку конденсатора. Второе уравнение это уравнение механических колебаний вискера с демпфером, но с учетом действующей на него электрической силы. В результате численного решения этих уравнений получаются результаты, представленные на рисунке. Видно, что вискер имеет гармоническую форму колебаний, а напряжения нет. Но период и частота совпадают.

  • Второй датчик рассчитан на измерение колебаний двойного вискера и на детектирование масс. Он состоит из двух вискеров, связанных между собой упругой перемычкой, каждый из которых подключен к своему конденсатору. Уравнение колебаний будут выглядеть следующим образом: [math] \begin{array}{l} m \ddot{x_1} + b \ddot{x_1} - \frac{C_1 u_1^2}{d}+\epsilon c (x_1 - x_2) = F(t) \\ m \ddot{x_2} + b \ddot{x_2} - \frac{C_2 u_2^2}{d}+\epsilon c (x_2 - x_1) = F(t) \\ U-R i_1-u_1c=0 \\ U-R i_2-u_2c=0 \end{array}[/math]

Эти уравнения отличаются от предыдущих тем, что в механической части добавилось слагаемое, отвечающее за упругую связь между вискерами. В результате интегрирования видно, что график напряжения полностью повторяет график механических колебаний, главное, что возможно точно измерить период огибающей биений, то есть померить массу с помощью напряжения.

  • Последний датчик предназначен для точного измерения колебаний одиночного вискера. Его особенность заключается в том, что один и тот же вискер выступает в роли обкладки для двух конденсаторов. Тогда выходной сигнал каждого из напряжений будет нелинейным, как и в первом случае, однако, если в качестве результата рассматривать разность напряжений на конденсаторах, то выходной сигнал получается гармоническим, точно совпадающим по частоте с колебаниями вискера, это дает возможность измерять частоту колебаний одиночного вискера с большой точностью. Уравнения колебаний такого датчика выглядят следующим образом: [math]m \ddot{x} + b \ddot{x} - \frac{C_1 u_1^2}{d}- \frac{C_2 u_2^2}{d} = F(t) \\ U-R i_1-u_1c=0 \\ U-R i_2-u_2c=0[/math]

  • Колебания вискера и напряжения в простейшем датчике

  • Колебания вискера и напряжения в датчике двойного вискера

  • Колебания вискера и напряжений в двойном датчике

  • Колебания вискера и разности напряжений в двойном датчике

Выводы[править]

В работе было рассмотрен и объяснён эксперимент с одиночным вискером, колеблющемся на игле; исследована и смоделирована система, состоящая из двух вискеров, соединённых упругим элементом; рассмотрены различные емкостные датчики колебаний.

Решение задачи об одиночном вискере, колеблющемся на игле, объясняет природу явления, зафиксированного в эксперименте, а так же предлагает метод приближённого решения подобных проблем. Метод решения (использования операторного подхода и разложения Галёркина) не увеличивает размерность задачи при увеличении количества искомых собственных частот, боле того, он учитывает особенности системы и позволяет находить только нужные собственные частоты и формы. Применить использованный подход можно так же и ко многим другим задачам.

Следующая задача, изученная в этой работе, это система из двух вискеров, связанных между собой упругой перемычкой, так называемый дифференциальный резонатор. Изученный дифференциальный резонатор имеет аналоги, которые обладают как своими преимуществами, так и недостатками, но основной принцип работы остаётся одинаковым, что подтверждается схожестью результатов исследования вискерного резонатора с его аналогами. Одним из преимуществ дифференциального резонатора, рассмотренного в этой работе, является способ его раскачки, гарантирующий получение достаточной для наблюдений амплитуды колебаний. Главным направлением применения такой конструкции является измерение масс наночатсиц.

Последним этапом проведённого исследования было изучение емкостных датчиков, с помощью которых можно производить измерения колебаний нановискеров. Изучено три вида датчиков. Все они основаны на использовании вискера в качестве одной из обкладок конденсатора, подключенного в электрическую цепь. Такие устройства позволяют измерять напряжение в сети, вместо измерения амплитуды или частоты колебаний самого вискера.

Все проведённое исследование основано на экспериментах с нановискерами и направлено на их улучшение и объяснение. Понимание процессов, происходящих при натурном исследовании нанообъектов позволяет упростить и усовершенствовать эксперименты, а также сократить количество неудачных, что ведет к значительной экономии денежных средств, материалов и времени учёных-эксперементаторов.


Список литературы[править]

  • Левичев В.В. Электронные и фотонные устройства: принцип работы, технологии изготов-

ления. //Учебник, учебное пособие, Год: 2015]

  • Я.С.Гринберг, Ю.А.Пашкин, Е.В.Ильичев. Наномеханические резонаторы.//Успехи фи-

зических наук. Т.182. №4. 2012.

  • Левичев В.В., Жуков М.В., Мухин И.С., Денисюк А.И., Голубок А.О. Об устойчивости

работы сканирующего силового микроскопа с нановискером на вершине зонда.// Журнал технической физики, 2013, том 83, вып. 7

  • Голубок А.О., Ковров А.В., Левичев В.В., Мухин И.С., Приходько О.А. Формирова-

ние одиночных нановискеров на вершинах зондов сканирующего зондового микроскопа. Научно-технический вестник Санкт-Петербургского государственного университета ин- формационных технологий, механики и оптики. 2009. № 4(62). С. 82-87. [Тип: Статья, Год: 2009]

  • Жилин П. А. Прикладная механика. Теория тонких упругих стержней: Учеб. пособие.

СПб.: Изд-во Политехн. ун-та, 2007. 101 с.

  • Фридман В. М. Теория упругих колебаний: уравнения и методы / В. М. Фридман ; Рос.

акад. наук, Ин-т проблем машиноведения. - Санкт-Петербург : Наука, 2014. - 253, [1] с.; 16 усл. печ. л. - Библиогр.: с. 248-250 (61 назв.). - 500 экз. - ISBN 978-5-02-038375-3 (в пер.)

  • Галёркин Б. Г. Стержни и пластинки. Ряды в некоторых вопросах упругого равновесия

стержней и пластинок. // Вестник инженеров. — 1915. — Т. 1. — С. 897—908.

  • Штукин Л.В., Беринский И.Е., Индейцев Д.А., Морозов Н.Ф., Скубов Д.Ю. Электроме-

ханические модели нанорезонаторов. //Физическая мезомеханика 19 1 2016г

  • И.Е. Бринский, Д.И. Индейцев, Н.Ф. Морозов, Д.Ю. Скубов, Л.В. Штукин. Дифферен-

циальный резонатор как детектор массы. // Механика твердого тела. №2 2015.

  • Д.И. Индейцев, О.С. Лобода, Н.Ф. Морозов, Д.Ю. Скубов, Л.В. Штукин. Автоколеба-

тельный режим нанорезонатора. //Физическая мезомеханика 19 5 2016г с. 23-28

  • Н. Ф. Морозов, И.Е. Бринский, Д.И. Индейцев, О.В. Привалова, Д.Ю. Скубов, Л.В. Шту-

кин. Срыв колебаний графенового резонатора, как способ определения его спектральных характеристик. ДОКЛАДЫ АКАДЕМИИ НАУК, 2014, том 456, № 5, с. 1–5 41

Источник — «http://tm.spbstu.ru/?title=Разработка_электро-механических_моделей_углеродных_нановискеров_как_детекторов_масс&oldid=47312»