Проект "Фехтование"

Описание

Актуальность

Фехтование в наши дни пользуется растущей популярностью.В современном мире все большее количество людей заинтересовано спортивным фехтованием.Также на многих сценах и экранах мира можно наблюдать эпизоды, проникнутые именно этим видом искусства.Стоит упомянуть и непосредственно реконструкцию, или, историческое фехтование, которое весьма популярно среди жаждущих воспроизведения страниц истории, связанных с холодным боевым оружием.

Проектная команда

• Дзенушко Дайнис
  
• Фролова Ксения
  
• Александров Сергей
  

Научный руководитель: Е.А. Иванова

Цели проекта

• Создание модели руки фехтовальщика т.е. модели руки которая по заданным конечным параметрам руки и виду удара воспроизводит этот удар
• Высокоскоростная съемка и анализ фехтовальных движений с целью создания видеоучебника

План

1. Создать модель которая по заданным параметрам (углам в суставах, координатам плеча) восстанавливает положение руки и приходит в него из любого положения (с визуализацией)
2. Определить ограничения движения руки в суставах
3. Снять технику фехтования на высокоскоростную камеру
4. Проанализировать технику и выявить набор простейших движений из которых состоят удары
5. Найти параметры элементарных движений от которых зависит то куда придется удар
6. Обучить модель простейшим движениям
7. Создать базу ударов и обучить им модель
8. Используя параметры выявленные в пункте 4 обучить модель по заданному конечному положению руки и виду удара проводить этот удар

Поэтапное решение задач

Постановка задач, решаемых в реальном времени:

Срок	Задача	Ответственные	Статус
7.03.12	Решение проблемы визуализации траектории движения руки (проблема вращения)	Дзенушко Дайнис	DONE
11.03.12	Оптимизация поворота руки по изменению угла	Дзенушко Дайнис	DONE
13.03.2012	Аналитическое описание простейшего действия - движения руки вперед из положения "согнута в локте" в положение "выпрямлена".Нахождение отношений угловых скоростей в суставах	Фролова Ксения	решение найдено
16.03.12	Первая встреча с представителями школы фехтования для обсуждения видения результатов проекта	Дзенушко Дайнис Фролова Ксения Александров Сергей	Well Done
20.03.12	Восстановление углов по заданным конечным координатам положения запястья	Фролова Ксения	решение частично найдено
19.03-2.04.12	Первая съёмка фехтования	Дзенушко Дайнис Фролова Ксения Александров Сергей	планируется
20.03-1.04.12	Написание простейшей версии интерфейса для модели (C# WPF) + триангуляция руки	Дзенушко Дайнис	Developing
3.04.12	Написание класса тензоров.Реализация представления тензора поворота, скалярного умножения тензоров и скалярного умножения тензора на вектор.	Фролова Ксения	в процессе реализации

Результаты проекта

Поэтапная отчетность по проделанной работе.Демонстрация полученных результатов / содержательное описание возникших в ходе работы сложностей и проблем.

• Восстановление положения руки по заданным параметрам
• Аналитическое описание движений руки
• Пробы съемки на высокоскоростную камеру
• Краткий отчет по поводу первой встречи с фехтовальщиками

Восстановление положения руки по заданным параметрам

Степени свободы

Наша модель руки имеет 9 степеней свободы:
2 — поступательное движение плеча (вперед/назад;вверх/вниз)
3 — плечевой сустав (сферический шарнир)
1 — локтевой сустав
1 — вращение кистью вокруг своей оси
2 — запястье (2 перпендикулярных цилиндрических шарнира)

Поворот руки

В нашем случае рука состоит из трех частей представленных тремя векторами:

1. Плечевая кость соответствует [math]\b{a}[/math]
2. Локтевая кость соответствует [math]\b{b}[/math]
3. Кисть соответствует [math]\b{c}[/math]

С ними связаны базисы base1; base2; base3 соответственно.
Изначальное положение руки - вытянутая горизонтально в право (правая рука), ось поворота локтя вертикальна
Повороты частей осуществляются посредством поворота соответствующего вектора вокруг определенной оси. Это достигается посредством скалярного умножения вектора слева на тензор поворота, который рассчитывается следующим образом
[math]\b{\b{P}}(\phi,e) = \b{e}\b{e} + (\b{\b{E}} - \b{e}\b{e})cos(\phi) + \b{e} \times \b{\b{E}}sin(\phi)[/math]
[math]\widetilde{\b{a}} = \b{\b{P}}(\xi,\widetilde{\widetilde{\b{k})}} \cdot\b{\b{P}}(\psi,\widetilde{\b{j})} \cdot\b{\b{P}}(\varphi,\b{i}) \cdot \b{a}[/math]
После этого необходимо также повернуть остальные (отстоящие еще дальше от плеча чем рассматриваемый) векторы и соответствующие им базисы также умножив их слева на тот же тензор поворота [math]\b{\b{P}}(\phi,e)[/math]
Таким образом осуществляется поворот всех 3х векторов на необходимые углы. Затем вычисляем координаты суставов:
[math]\b{o}[/math] — радиус-вектор плеча;
локоть: [math]\b{r} = \b{o}+\b{a}[/math]
запястье: [math]\b{r} = \b{o}+\b{a}+\b{b}[/math]
кончик кисти: [math]\b{r} = \b{o}+\b{a}+\b{b}+\b{c}[/math]

Вращение

Визуализация движения подразумевает нахождение траектории движения. Здесь мы встретили проблему: необходимо разбить весь поворот на малые, последовательное применение которых в конечном итоге и приведет руку в заданное положение и при этом мы получим траекторию движения. Если мы просто разделим углы на количество шагов и будем каждый раз поворачивать руку на эти малые углы то в случае когда каждый сустав вращается вокруг только одной оси все будет хорошо, но в случае поворота вокруг двух и более осей вместе с поворотом вектора также будет вращаться и связанный с ним базис в результате каждый следующий малый поворот будет осуществляться вокруг уже немного повернутых осей и мы придем уже в другое положение чем если мы один раз применим тензор поворота с полными углами.
Решение:
Решение оказалось довольно таки простым и не усложнило программу. Теперь вместо того чтобы поворачивать руку на небольшие углы а потом из нового положения поворачивать ее дальше было решено поворачивать руку на каждом шаге из начальной точки траектории с каждым шагом все на большие углы. Т.е. разбив полные углы поворота на несколько частей (малые углы ,количество которых равно количеству шагов) на каждом шаге мы поворачиваем из начального положения руку на углы равные [math]\varphi_i = \Delta \varphi\cdot i[/math] где i - порядковый номер шага.
Оптимизация траектории:
Возникла идея оптимизировать траекторию движения. Имеется в виду оптимизация по изменению угла. Т.е. сделать так чтобы система осуществляла переход в новое положение таким образом что изменение углов в суставах было бы минимальным.
Рассмотрим на примере плечевой кости. Для оптимизации скачала определяем конечное положение соответствующего вектора. Затем векторно умножаем начальный вектор на конечный, так определяем ось вращения и синус угла между векторами. Потом умножаем их скалярно, откуда получаем косинус угла. Используя синус и косинус определяем сам угол. Делим угол на количество шагов. затем осуществляем вращение вокруг найденной оси на найденный угол. В результате поворот осуществляется на минимальный угол.

Реализация поворота в пакете MATLAB

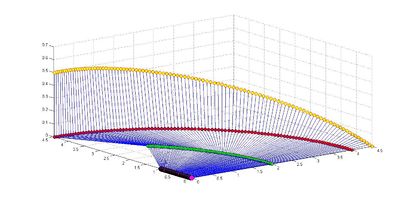
Используя пакет MATLAB был реализован данный алгоритм поворота с целью построить траекторию движения руки и проверить правильность алгоритма. Все вполне правдоподобно выглядит.
Пример движения руки:

• 



истории, связанных с холодным боевым оружием.

Аналитическое описание движений руки

Описание движения руки вперед из положения "согнута в локте" в положение "выпрямлена". Нахождение отношений угловых скоростей в суставах

Формулировка задачи и ее формализация
Исходя из заданного начального положения руки, определить, каковыми должны быть отношения угловых скоростей в суставах, чтобы удар был прямым.Таким образом, имеются начальные углы, под которыми согнута рука в трех суставах. Необходимо также найти возможную зависимость начальных углов друг от друга и определить, от каких начальных углов зависят конечные, соответствующие выпрямленному положению руки. Расчеты проводятся для 2D - случая.
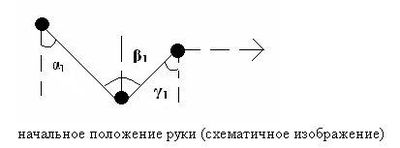
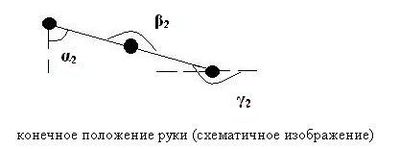
Схематичная демонстрация положения руки в начальном положении и в конечном (до проведения удара и после проведения прямого удара):

• 
• 



Нахождение отношений угловых частот "в лоб"
В конечном положении рука выпрямлена, то есть угол в локте, соответствующий [math]\beta2[/math], составляет [math]\pi[/math] радиан;
Рассмотрим угол [math]\gamma2[/math]. Из геометрических соображений он будет равен [math]\pi/2 - \alpha2 + \pi = 3*\pi/2 - \alpha2[/math]
Таким образом, мы получаем выражения для угловых частот в суставах:
[math]\omega_1 = (\alpha_{2} - \alpha_{1})/t[/math] (рад/с)
[math]\omega2 = (\beta2 - \beta1)/t = (\pi - \beta1)/t[/math] (рад/с)
[math]\omega3 = (\gamma2 - \gamma1)/t = (3*\pi/2 - \alpha2 - \gamma1)/t[/math] (рад/с)
Далее нахождение непосредственно интересующих нас отношений выраженных угловых частот [math]\omega1, \omega2, \omega3[/math]: [math]\omega1/\omega2 = (\alpha2 - \alpha1)/(\pi - \beta1)[/math]
[math]\omega2/\omega3 = (\pi - \beta1)/(3*\pi/2 - \alpha2 - \gamma1)[/math]
[math]\omega3/\omega1 = (3*\pi/2 - \alpha2 - \gamma1)/(\alpha2 - \alpha1)[/math]
Выявление зависимостей углов друг от друга
Из выше представленных формул видно, что
отношение [math]\omega1/\omega2[/math] зависит от углов [math]\alpha1,\alpha2,\beta1[/math];
отношение [math]\omega2/\omega3[/math] зависит от углов [math]\beta1,\alpha2,\gamma1[/math];
отношение [math]\omega3/\omega1[/math] зависит от углов [math]\alpha1,\alpha2,\gamma1[/math];
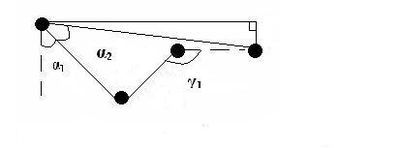
Рассмотрим угол [math]\beta1[/math]:
Из рисунка, демонстрирующего начальное схематичное положение руки, видно, что [math]\beta1 = \alpha1 + (\gamma1 - \pi/2)[/math]. Таким образом, угол [math]\beta1[/math] зависит от углов [math]\alpha1 и \gamma1[/math].
Из логических соображений нетрудно понять, что в свою очередь углы [math]\alpha1, \gamma1[/math] не зависят друг от друга. То есть начальное положение руки определяется двумя углами.
Рассмотрим зависимость конечного угла [math]\alpha2[/math] от начального положения руки (зависимость от углов [math]\alpha1,\gamma1[/math]):

• 



Из рисунка видно, что [math]\alpha2 = \pi/2 - \alpha1 - (\pi/2 - (\pi/2 - (\gamma1 - \pi))) = \pi/2 - \alpha1 - (\pi/2 - (3*\pi/2 - \gamma1))= \pi/2 - \alpha1 - (\gamma1 - \pi) = 3*\pi/2 - \alpha1 - \gamma1[/math]
Таким образом, угол [math]\alpha2[/math] зависит от углов [math]\alpha1,\gamma1[/math]
Окончательные результаты
[math]\omega1/\omega2 = (3*\pi/2 - \alpha1 - \gamma1 - \alpha1)/(3*\pi/2 - \alpha1 - \gamma1) = (3*\pi/2 - 2*\alpha1 - \gamma1)/(3*\pi/2 - \alpha1 - \gamma1) = 1 - \alpha1/(3*\pi/2 - \alpha1 - \gamma1)[/math];

[math]\omega2/\omega3 = (3*\pi/2 - \alpha1 - \gamma1)/(3*\pi/2 - 3*\pi/2 + \alpha1 + \gamma1 - \gamma1) = (3*\pi/2 - \alpha1 - \gamma1)/\alpha1 = 3*\pi/(2* \alpha1) - \gamma1/\alpha1 - 1[/math];

[math]\omega3/\omega1 = (3*\pi/2 - 3*\pi/2 + \alpha1 + \gamma1 - \gamma1)/(3*\pi/2 - 2*\alpha1 - \gamma1) = \alpha1/(3*\pi/2 - 2*\alpha1 - \gamma1) [/math];

Из чего следует, что [math]\omega1/\omega3 = 3*\pi/(2*\alpha1) - \gamma1/\alpha1 - 2[/math]
Возникшие затруднения:
Найденное выше решение соответствует конечному положению руки фехтовальщика. Найденное соотношение угловых скоростей действительно характеризует соотношение угловых скоростей в конце движения, а также конечные углы найдены в правильной зависимости от начальных заданных. Но нам неизвестна тракектория движения в процессе перехода от начального положения руки фехтовальщика к конечному. В следствие этого возникает необходимость подсчета поэтапных изменений угловых скоростей, иными словами - зависимостей изменений углов в суставах от времени в любой его момент с целью воссоздания не просто нужного конечного положения руки, но также необходимого движеня как такового.
Для нахождения непрерывных зависимостей необходимо рассматривать начальное положение, положение, в которое рука должна прийти (то есть нужно использовать уже найденное решение), а также необходимо учитывать, что в любой момент времени и производимых рассчетов, скорость сустава, соответствующего "запястью", должна быть равной значению "0" по оси y.

Восстановление углов по заданным конечным координатам положения запястья

2D - задача

Необходимо решить обратную задачу. То есть восстановить углы,которые необходимо задать для последующего перемещения запястья в точку с указанными координатами.По конечному положению определить, каковыми должны быть начальные заданные условия для осуществления движения руки.
Дано:
[math]\b{a} = a*cos\phi*\b{i}+a*sin\phi*\b{j}[/math]
[math]\b{b} = b*cos(\phi+\psi)*\b{i}+b*sin(\phi+\psi)*\b{j}[/math]
[math]\b{a}+\b{b}=\b{r}[/math]
Таким образом, получаем, что:
[math]x = a_i+b_i[/math]
[math]y = a_j+b_j[/math]
То есть:
[math]x = a*cos\phi + b*cos(\phi+\psi)[/math]
[math]y = a*sin\phi + b*sin(\phi+\psi)[/math]
Решим систему относительно угла [math]\psi[/math] посредством возведения в квадрат уравнений относительно x и относительно y, а затем сложения их.
[math]x^{2} = a^{2}*cos^{2}\phi + 2*a*cos\phi*b*cos(\phi+\psi) + b^{2}*cos^{2}(\phi+\psi)[/math]
[math]y^{2} = a^{2}*sin^{2}\phi + 2*a*sin\phi*b*sin(\phi+\psi) + b^{2}*sin^{2}(\phi+\psi)[/math]
[math]x^{2}+y^{2} = a^{2} + 2*a*b*cos\phi*cos(\phi+\psi) + 2*a*b*sin\phi*sin(\phi+\psi) + b^{2}[/math]
[math]\frac{x^{2}+y^{2}-a^{2}-b^{2}}{2*a*b} = cos\phi*cos(\phi+\psi) + sin\phi*sin(\phi+\psi)[/math]
[math]\frac{x^{2}+y^{2}-a^{2}-b^{2}}{2*a*b} = cos\phi*(cos\psi*cos\phi - sin\psi*sin\phi) + sin\phi*(cos\phi*sin\psi + sin\phi*cos\psi)[/math]
[math]\frac{x^{2}+y^{2}-a^{2}-b^{2}}{2*a*b} = cos^{2}\phi*cos\psi - sin\psi*sin\phi*cos\phi + sin\psi*sin\phi*cos\phi + sin^{2}\phi*cos\psi[/math]
[math]cos\psi = \frac{x^{2}+y^{2}-a^{2}-b^{2}}{2*a*b}[/math]
Следовательно,
[math]\psi = arccos(\frac{x^{2}+y^{2}-a^{2}-b^{2}}{2*a*b})[/math]

Реализация модели на C#

В данный момент ведется работа по написанию модели на C#(WPF). Подразумевается создание интерфейса и хорошей визуализации. Для визуализации требуется 3D модель руки которая получается путем триангуляции (составлением из треугольников).

Класс тензоров

Возникла необходимость написания класса тензоров для последующего использования его при реализации графической визуализации движения руки.
При реализации этого движения мы будем использовать тензор поворота. Таким образом, в классе "тензор" должны присутствовать следующие методы:

• Метод,возвращающий тензор поворота типа "тензор" по заданному углу поворота и координатам конца вектора вращения;
  
• Метод, возвращающий скалярное произведение тензоров типа "тензор" по двум заданным тензорам;
  
• Метод, возвращающий скалярное произведение тензора и вектора типа "вектор" по заданному тензору и вектору.
  

Примечание:
для последующей реализации визуализации движения руки необходимо использовать существующий тип Vector3D и новый тип Tenzor. Объект типа Tenzor представляется массивом из трех объектов типа Vector3D. Таким образом, обращение к одному из девяти элементов тензора по строке и столбцу будет происходить по полям .X,.Y,.Z и по индексам 0,1,2 соответственно.

Краткий отчет по поводу первой встречи с фехтовальщиками

1.Высокоскоростная съемка.
В технике фехтования оновополагающим элементом является траектория удара. Часто удары проводятся на большой скорости, а потому многие нюансы не видны глазу, при том, что провести этот же удар на более медленной скорости, не утратив при этом сам принцип, не представляется возможным. Этот факт и стал основной причиной необходимости введения высокоскоростной съемки. В последствие на основе снятого материала будет необходимо составить видеоучебник, который будет как разъяснять нюансы скоростных ударов ученикам, так и позволит освоить некоторые навыки самостоятельно, поскольку не все имеют возможность тренироваться под руководством тернера на постоянной основе. Для создания качественного учебника нужно будет обработать заснятый материал, проприсовав траекторию и отметив некотоыре точки в пространстве.
Таким образом, на повестке дня находтися высокоскоростная съемка с качественным изображением для наглядной демонстрации, а также приобретение навыков по обработке заснятого материала с помощью специальных средств и пакетов.
2.Создание робота.
Робот будет создан для фехтовальщиков, практикующших колющие удары, то есть для людей, тренирующихся на шпагах.
В качестве начального этапа мы рассматриваем возможность создания робота, обладающего одной степенью свободы. Мы рассматриваем только один шарнир, соответствующий "запястью", совершающий при этом движения в одной плоскости из стороны в сторону. В качестве "усовершенствования" робота можно будет добавить впоследствии роботу еще одну степень свободы для совершения колебаний как в горизонтальной плоскости, так и в вертикальной.

См. также

• Высокоскоростная видеокамера
• Научные работы студентов