Переход к тепловому равновесию в гармонической ГЦК решетке — различия между версиями
(→Вывод уравнений) |
|||
| Строка 20: | Строка 20: | ||
===Вывод уравнений=== | ===Вывод уравнений=== | ||
| − | Рассмотрим кристаллическую ГЦК решетку, состоящую из одинаковых частиц массой <math> m </math>, соединенных линейными пружинками жесткостью <math> c </math>. Уравнения движения частицы с радиус-вектором <math> \textbf{r} </math> имеют следующий вид: <br /> <math> \textbf{u}(\textbf{r}) = \sum_\alpha \textbf{C}_\alpha \textbf{u}(\textbf{r}+\textbf{n}_\alpha)</math>, <br /> | + | Рассмотрим кристаллическую ГЦК решетку, состоящую из одинаковых частиц массой <math> m </math>, соединенных линейными пружинками жесткостью <math> c </math>. Уравнения движения частицы с радиус-вектором <math> \textbf{r} </math> имеют следующий вид: <br /> <math> \ddot{\textbf{u}}(\textbf{r}) = \sum_\alpha \textbf{C}_\alpha \textbf{u}(\textbf{r}+\textbf{n}_\alpha)</math>, <br /> |
где <math> \textbf{u}(\textbf{r}) = (u_x, u_y, u_z)^\top </math> - вектор-столбец, состоящий из компонент вектора перемещения частицы с радиус-вектором <math> \textbf{r} </math>, <math> \textbf{C}_\alpha </math> - матрицы, коэффициенты которых определяют вклад частицы номер <math> \alpha </math> в суммарную силу, действующую на частицу с радиус-вектором <math> \textbf{r} </math>. <br /> | где <math> \textbf{u}(\textbf{r}) = (u_x, u_y, u_z)^\top </math> - вектор-столбец, состоящий из компонент вектора перемещения частицы с радиус-вектором <math> \textbf{r} </math>, <math> \textbf{C}_\alpha </math> - матрицы, коэффициенты которых определяют вклад частицы номер <math> \alpha </math> в суммарную силу, действующую на частицу с радиус-вектором <math> \textbf{r} </math>. <br /> | ||
Сделаем следующую подстановку в уравнение движения для получения дисперсионного соотношения <math> \omega </math>: <br /> | Сделаем следующую подстановку в уравнение движения для получения дисперсионного соотношения <math> \omega </math>: <br /> | ||
| Строка 28: | Строка 28: | ||
<math> \textbf{D} = -\frac{1}{m} \sum_\alpha \textbf{C}_\alpha e^{\textbf{k} \cdot \textbf{a}_\alpha}. \omega^2_j </math> - собственные числа матрицы <math> \textbf{D} </math>. С помощью них можно получить следующую формулу для кинетической температуры <math> T </math>: | <math> \textbf{D} = -\frac{1}{m} \sum_\alpha \textbf{C}_\alpha e^{\textbf{k} \cdot \textbf{a}_\alpha}. \omega^2_j </math> - собственные числа матрицы <math> \textbf{D} </math>. С помощью них можно получить следующую формулу для кинетической температуры <math> T </math>: | ||
<math> T = \frac{T_0}{2} + B_1 + B_2 + B_3, \quad B_j = \int_\textbf{k} (\textrm{cos} (2\omega_j t)) \textrm{d} \textbf{k} </math>. <br /> | <math> T = \frac{T_0}{2} + B_1 + B_2 + B_3, \quad B_j = \int_\textbf{k} (\textrm{cos} (2\omega_j t)) \textrm{d} \textbf{k} </math>. <br /> | ||
| − | |||
===Результаты=== | ===Результаты=== | ||
Версия 12:54, 24 января 2019
Курсовой проект по Механике дискретных сред
Исполнитель: Ляжков Сергей
Группа: 43604/1
Семестр: осень 2018
Содержание
Постановка задачи
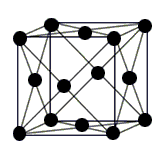
Рассмотреть поведение кинетической температуры при переходе к тепловому равновесию в бесконечной гармонической гранецентрированной кубической (ГЦК) решетке при следующих начальных условиях:
- Частицы имеют нулевые перемещения.
- Частицы имеют случайные скорости.
- Распределение температуры - однородное.
- Кинетические температуры, соответствующие различным пространственным направлениям, не равны.
Вывод уравнений
Рассмотрим кристаллическую ГЦК решетку, состоящую из одинаковых частиц массой , соединенных линейными пружинками жесткостью . Уравнения движения частицы с радиус-вектором имеют следующий вид:
,
где - вектор-столбец, состоящий из компонент вектора перемещения частицы с радиус-вектором , - матрицы, коэффициенты которых определяют вклад частицы номер в суммарную силу, действующую на частицу с радиус-вектором .
Сделаем следующую подстановку в уравнение движения для получения дисперсионного соотношения :
,
где - волновой вектор, и получим динамическую матрицу :
- собственные числа матрицы . С помощью них можно получить следующую формулу для кинетической температуры :
.
Результаты
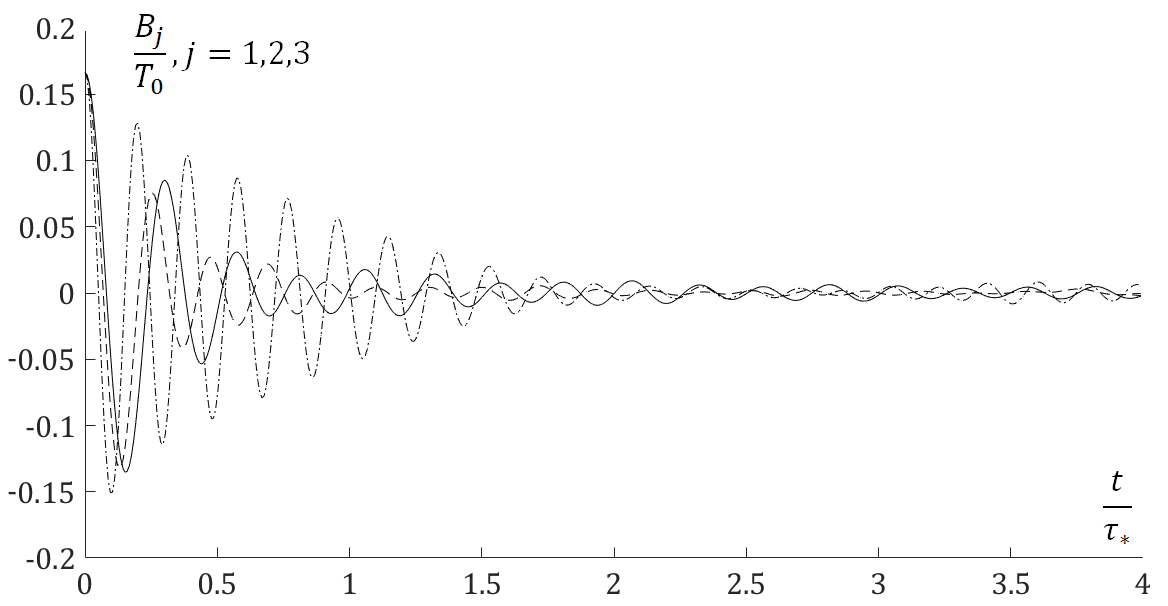
Вклады веток дисперсионного соотношения в колебания температуры:
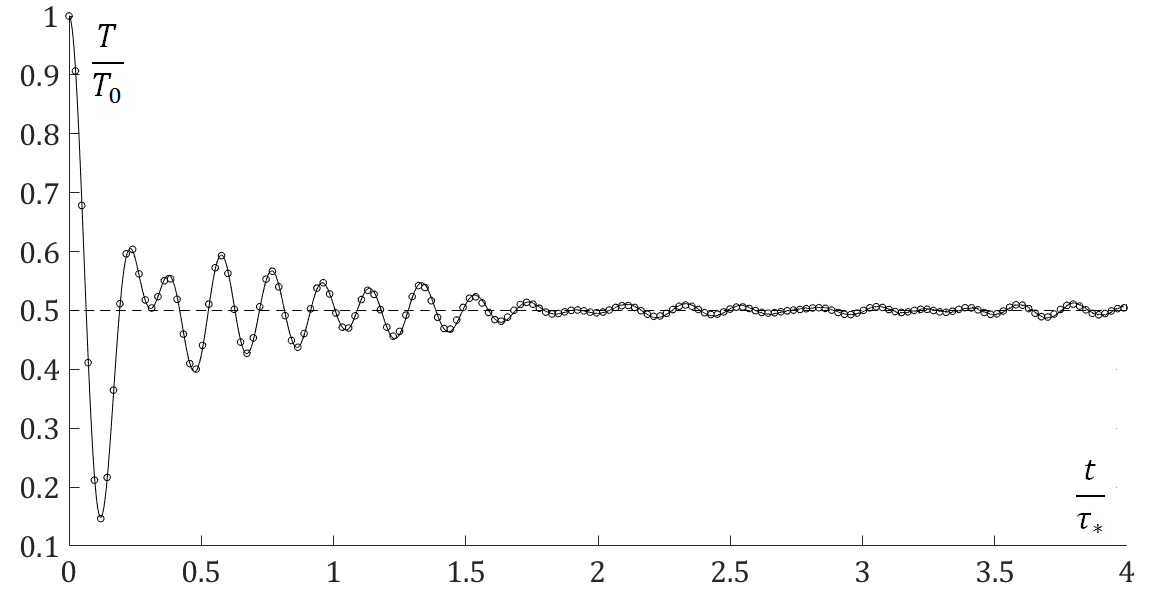
Колебания кинетической температуры, связанные с выравниванием кинетической и потенциальной энергий:
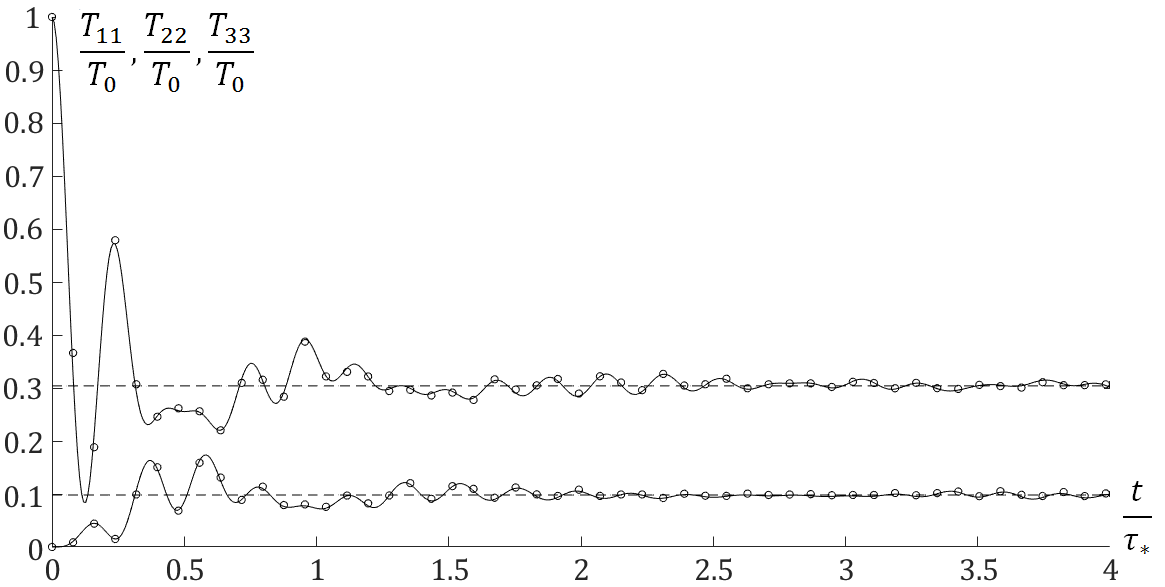
Перераспределение кинетической температуры по пространственным направлениям:
Линии - аналитическое решения по формулам, представленным в нижеприведенной статье, точки - численное решение уравнения динамики решетки.
Текст статьи
Переход к тепловому равновесию в гармонической гранецентрированной кубической решетке
Неделя науки 2018
Данный проект был представлен на конференции "Неделя науки 2018".