Перераспределение энергии между степенями свободы в нелинейной двухатомной цепочке — различия между версиями
Anpolol (обсуждение | вклад) (→Решение) |
Anpolol (обсуждение | вклад) (→Выводы) |
||
| (не показано 5 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | =Постановка задачи= | + | [[ Курсовые_работы_по_ВМДС:_2018-2019 | Курсовые работы 2018-2019 учебного года]] > '''Перераспределение энергии между степенями свободы в нелинейной двухатомной цепочке''' <HR> |
| + | |||
| + | '''''Курсовой проект по [[Механика дискретных сред|Механике дискретных сред]]''''' | ||
| + | |||
| + | '''Исполнитель:''' [[Белоусова Екатерина]] | ||
| + | |||
| + | '''Группа:''' 43604/1 | ||
| + | |||
| + | '''Семестр:''' осень 2018 | ||
| + | |||
| + | ===Постановка задачи=== | ||
| + | |||
Рассмотреть перераспределение энергии между степенями свободы в нелинейной двухатомной цепочке, построить графики зависимости энергии частиц от времени. | Рассмотреть перераспределение энергии между степенями свободы в нелинейной двухатомной цепочке, построить графики зависимости энергии частиц от времени. | ||
| − | =Решение= | + | |
| − | Рассмотрим модель колебаний одномерной двухатомной цепочки массами | + | ===Решение=== |
| + | |||
| + | Рассмотрим модель колебаний одномерной двухатомной цепочки массами <math> m_{1} </math> и <math> m_{2} </math>. Пусть в этой цепочке находится N атомов. Обозначим смещение n-го атома <math> u_n </math>, а атома, отстоящего от него на p узлов, <math> u_{n+p} </math>. Примем в качестве положительных смещения атомов вправо от положения равновесия, а отрицательных – влево. | ||
[[File:Ри1111.png|center]] | [[File:Ри1111.png|center]] | ||
Каждый атом смещается только вдоль цепочки, что следует из требования одномерности модели. | Каждый атом смещается только вдоль цепочки, что следует из требования одномерности модели. | ||
Пусть атомы связаны между собой упругой силой F с коэффициентом упругости с. Найдем уравнение движения n-го и n+1-го атома в цепи. В равновесном положении силы, действующие на атомы, равны нулю. При произвольных смещениях на каждый n-й атом будет действовать сила со стороны соседних атомов. Суммарную силу, действующую на n-й атом со стороны соседних атомов, можно представить в виде:<br /> | Пусть атомы связаны между собой упругой силой F с коэффициентом упругости с. Найдем уравнение движения n-го и n+1-го атома в цепи. В равновесном положении силы, действующие на атомы, равны нулю. При произвольных смещениях на каждый n-й атом будет действовать сила со стороны соседних атомов. Суммарную силу, действующую на n-й атом со стороны соседних атомов, можно представить в виде:<br /> | ||
<math> | <math> | ||
| − | F_n=F_{n,n+1}-F_{n-1,n}=c(u_{n+1}-2u_n+u_{n-1} | + | F_n=F_{n,n+1}-F_{n-1,n}=c(u_{n+1}-2u_n+u_{n-1}) |
</math><br /> | </math><br /> | ||
| − | Запишем систему уравнений движения атомов массой <math> m_{1} </math> и <math> m_{2} </math><br /> | + | Запишем систему уравнений движения атомов массой <math> m_{1} </math> и <math> m_{2} </math>:<br /> |
<math> | <math> | ||
m_{1} \frac{d^2 u_{2n-1}}{dt^2}=c(u_{2n}-2u_{2n-1}+u_{2n-2}) | m_{1} \frac{d^2 u_{2n-1}}{dt^2}=c(u_{2n}-2u_{2n-1}+u_{2n-2}) | ||
| Строка 16: | Строка 29: | ||
m_{2} \frac{d^2 u_{2n}}{dt^2}=c(u_{2n+1}-2u_{2n}+u_{2n-1}) | m_{2} \frac{d^2 u_{2n}}{dt^2}=c(u_{2n+1}-2u_{2n}+u_{2n-1}) | ||
</math><br /> | </math><br /> | ||
| − | + | В качестве начальных условий заданы случайные начальные скорости таким образом, что средняя скорость всех частиц равна 0. Перемещения всех частиц в начальный момент времени равны нулю. Также заданы периодические граничные условия на перемещения.<br /> | |
| − | + | <math> | |
| − | + | u_{n}(t=0)=0 | |
| − | + | </math><br /> | |
| − | В качестве начальных условий заданы случайные начальные скорости таким образом, что средняя скорость всех частиц равна 0. Перемещения всех частиц в начальный момент времени равны нулю. Также заданы периодические граничные условия на перемещения. | + | <math> |
| − | + | v_n(t=0) - случайные | |
| − | + | </math><br /> | |
| − | + | <math> | |
| − | + | u_{n+N}=u_n | |
| − | Система | + | </math><br /> |
| + | <math> | ||
| + | u_N=u_0 | ||
| + | </math><br /> | ||
| + | Система решалась в Matlab методом конечных разностей. | ||
В задаче на каждом шаге по времени находилась кинетическая энергия всей системы, после чего был построен график зависимости энергии системы от времени. | В задаче на каждом шаге по времени находилась кинетическая энергия всей системы, после чего был построен график зависимости энергии системы от времени. | ||
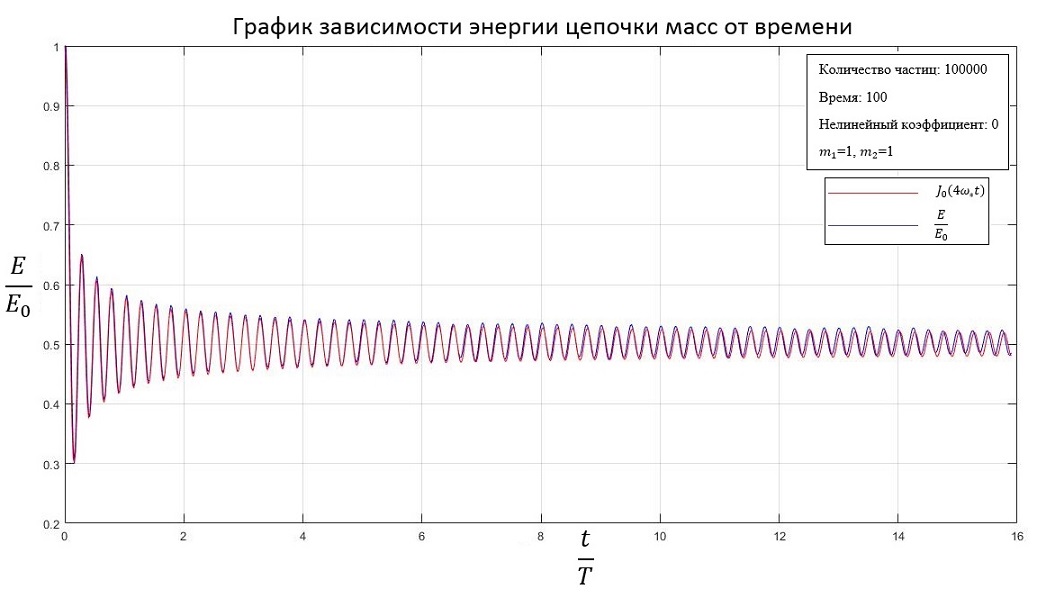
Для частиц одинаковой массы был получен следующий график: | Для частиц одинаковой массы был получен следующий график: | ||
[[File:Одинаковые массы..jpg|center]] | [[File:Одинаковые массы..jpg|center]] | ||
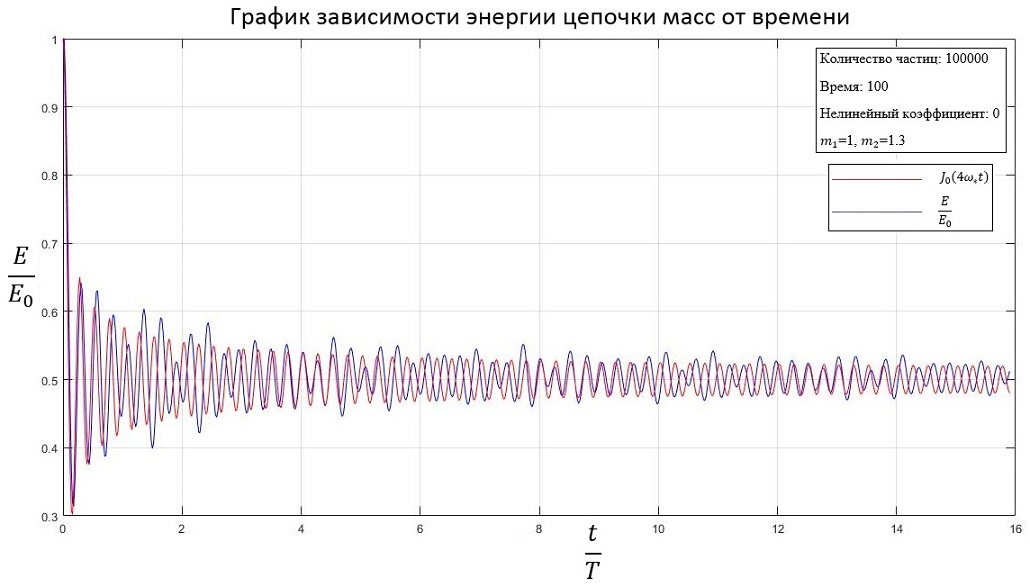
| − | Если рассматривать частицы разной массы, то график зависимости будет иметь следующий вид ( | + | Если рассматривать частицы разной массы, то график зависимости будет иметь следующий вид (<math> m_{1}=1 </math> и <math> m_{2}=1.3 </math>): |
[[File:M1=1 m2=1.3..jpg|center]] | [[File:M1=1 m2=1.3..jpg|center]] | ||
| − | Рассмотрим нелинейную постановку задачи. В выражении для силы будет присутствовать слагаемое третьего порядка: | + | Рассмотрим нелинейную постановку задачи. В выражении для силы будет присутствовать слагаемое третьего порядка:<br /> |
| − | + | <math> | |
| + | F_n=F_{n,n+1}-F_{n-1,n}=c(u_{n+1}-2u_n+u_{n-1})+b(u_{n+1}-u_n)^3-b(u_{n}-u_{n-1})^3 | ||
| + | </math><br /> | ||
Решается данная задача в нелинейной постановке аналогичным образом. если мы возьмем нелинейный коэффициент b равным нулю, получим решение, соответствующее предыдущей задаче. Начнем постепенно увеличивать коэффициент b и заметим, что система начнет затухать быстрее. | Решается данная задача в нелинейной постановке аналогичным образом. если мы возьмем нелинейный коэффициент b равным нулю, получим решение, соответствующее предыдущей задаче. Начнем постепенно увеличивать коэффициент b и заметим, что система начнет затухать быстрее. | ||
При одинаковой массе частиц: | При одинаковой массе частиц: | ||
| Строка 43: | Строка 62: | ||
b=1 | b=1 | ||
[[File:B=1..jpg|center]] | [[File:B=1..jpg|center]] | ||
| − | Разные массы частиц ( | + | Разные массы частиц (<math> m_{1}=1 </math> и <math> m_{2}=1.3 </math>):<br /> |
b=0.01 | b=0.01 | ||
[[File:M1=1 m2=1.3 b=0.01..jpg|center]] | [[File:M1=1 m2=1.3 b=0.01..jpg|center]] | ||
| Строка 53: | Строка 72: | ||
[[File:M1=1 m2=1.3 b=1..jpg|center]] | [[File:M1=1 m2=1.3 b=1..jpg|center]] | ||
| − | = | + | ===Выводы=== |
| − | + | ||
| + | Таким образом, в ходе реализации данной работы можно сделать следующие выводы: | ||
| + | |||
| + | 1. Для линейной системы с равными массами частиц график распределения кинетической энергии совпадает с функцией Бесселя нулевого порядка; | ||
| + | |||
| + | 2. Для нелинейной системы с увеличением коэффициента нелинейности кинетическая энергия стабилизируется на большем значении, чем для линейной системы. | ||
== См. также == | == См. также == | ||
| − | [[Кафедра "Теоретическая механика"]] | + | |
| + | *[[Кафедра "Теоретическая механика"]] | ||
| + | *[[Курсовые работы по ВМДС: 2018-2019]] | ||
| + | *[[Введение в механику дискретных сред]] | ||
Текущая версия на 11:37, 24 января 2019
Курсовые работы 2018-2019 учебного года > Перераспределение энергии между степенями свободы в нелинейной двухатомной цепочкеКурсовой проект по Механике дискретных сред
Исполнитель: Белоусова Екатерина
Группа: 43604/1
Семестр: осень 2018
Содержание
Постановка задачи[править]
Рассмотреть перераспределение энергии между степенями свободы в нелинейной двухатомной цепочке, построить графики зависимости энергии частиц от времени.
Решение[править]
Рассмотрим модель колебаний одномерной двухатомной цепочки массами и . Пусть в этой цепочке находится N атомов. Обозначим смещение n-го атома , а атома, отстоящего от него на p узлов, . Примем в качестве положительных смещения атомов вправо от положения равновесия, а отрицательных – влево.
Каждый атом смещается только вдоль цепочки, что следует из требования одномерности модели.
Пусть атомы связаны между собой упругой силой F с коэффициентом упругости с. Найдем уравнение движения n-го и n+1-го атома в цепи. В равновесном положении силы, действующие на атомы, равны нулю. При произвольных смещениях на каждый n-й атом будет действовать сила со стороны соседних атомов. Суммарную силу, действующую на n-й атом со стороны соседних атомов, можно представить в виде:
Запишем систему уравнений движения атомов массой и :
В качестве начальных условий заданы случайные начальные скорости таким образом, что средняя скорость всех частиц равна 0. Перемещения всех частиц в начальный момент времени равны нулю. Также заданы периодические граничные условия на перемещения.
Система решалась в Matlab методом конечных разностей.
В задаче на каждом шаге по времени находилась кинетическая энергия всей системы, после чего был построен график зависимости энергии системы от времени.
Для частиц одинаковой массы был получен следующий график:
Если рассматривать частицы разной массы, то график зависимости будет иметь следующий вид ( и ):
Рассмотрим нелинейную постановку задачи. В выражении для силы будет присутствовать слагаемое третьего порядка:
Решается данная задача в нелинейной постановке аналогичным образом. если мы возьмем нелинейный коэффициент b равным нулю, получим решение, соответствующее предыдущей задаче. Начнем постепенно увеличивать коэффициент b и заметим, что система начнет затухать быстрее.
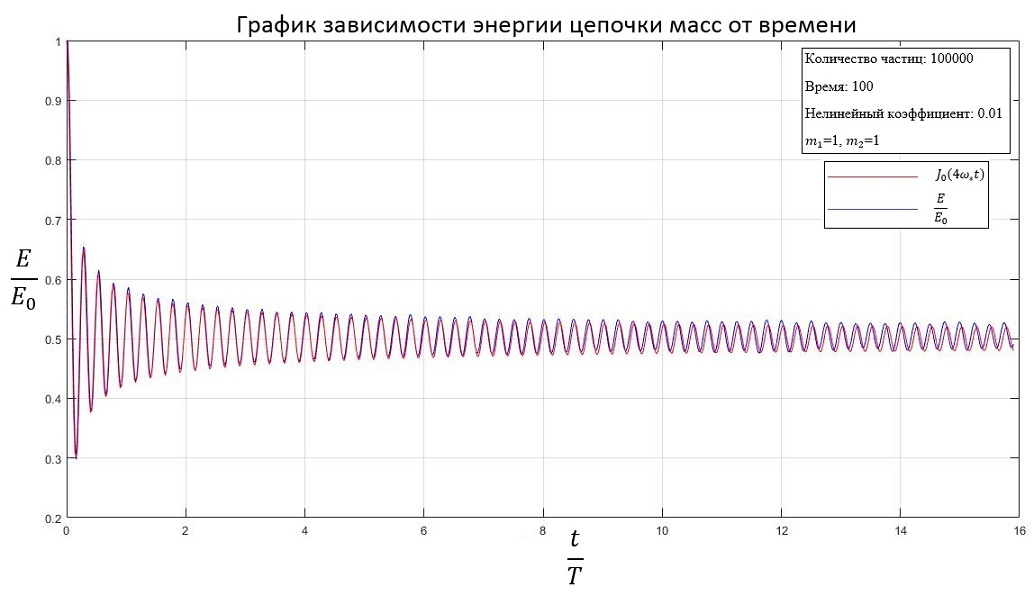
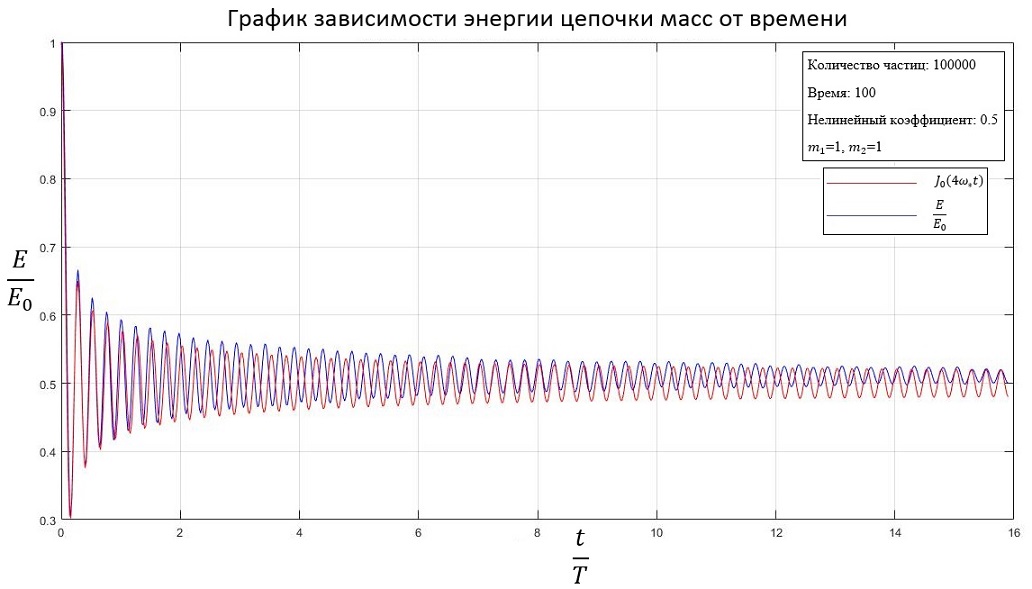
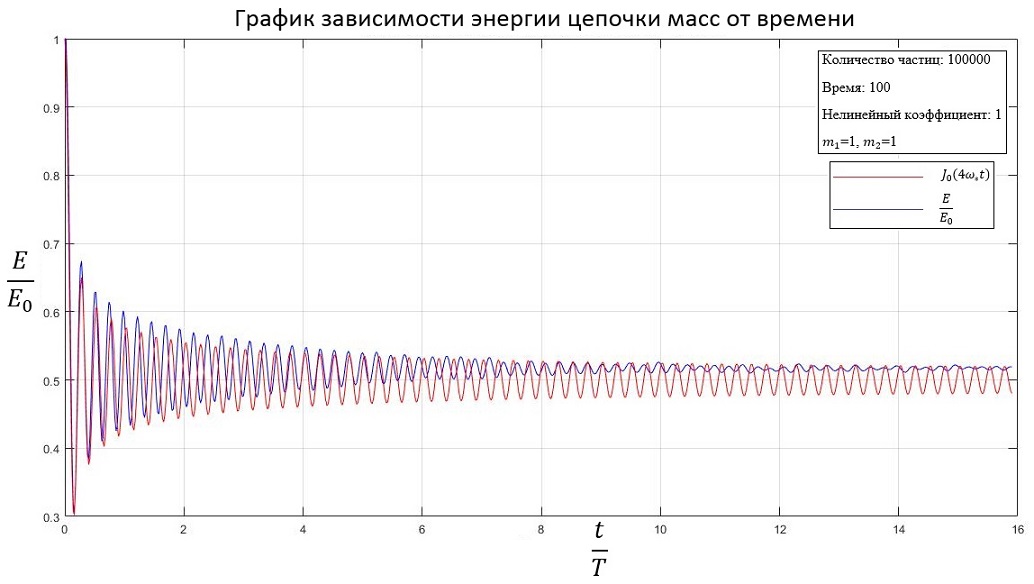
При одинаковой массе частиц:
b=0.01
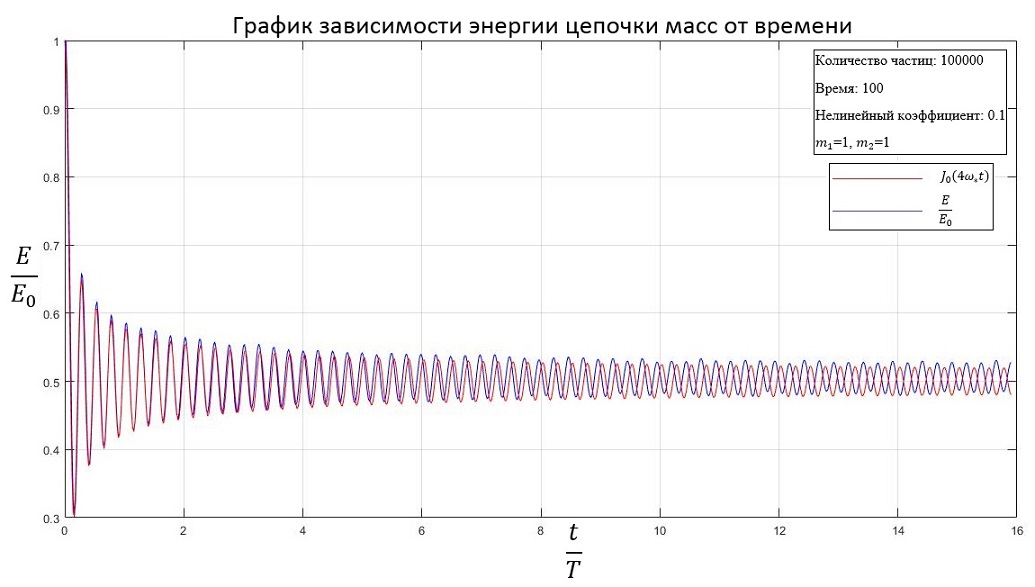
b=0.1
b=0.5
b=1
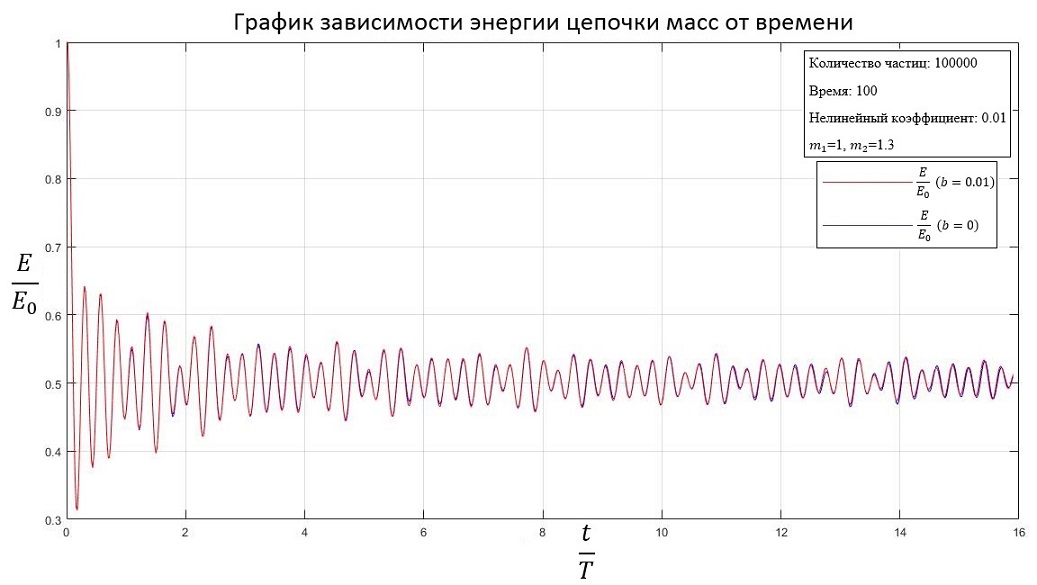
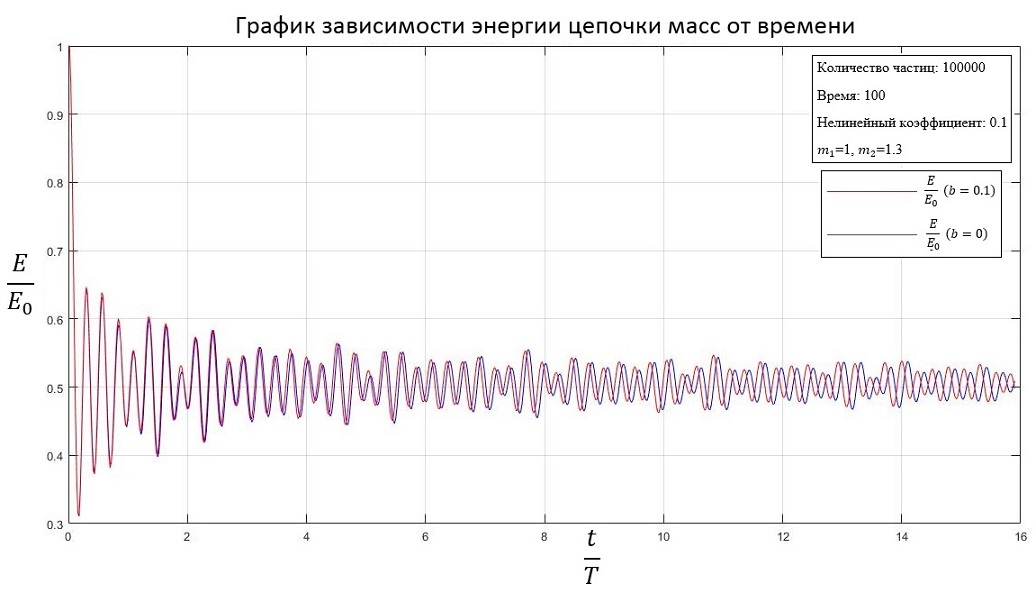
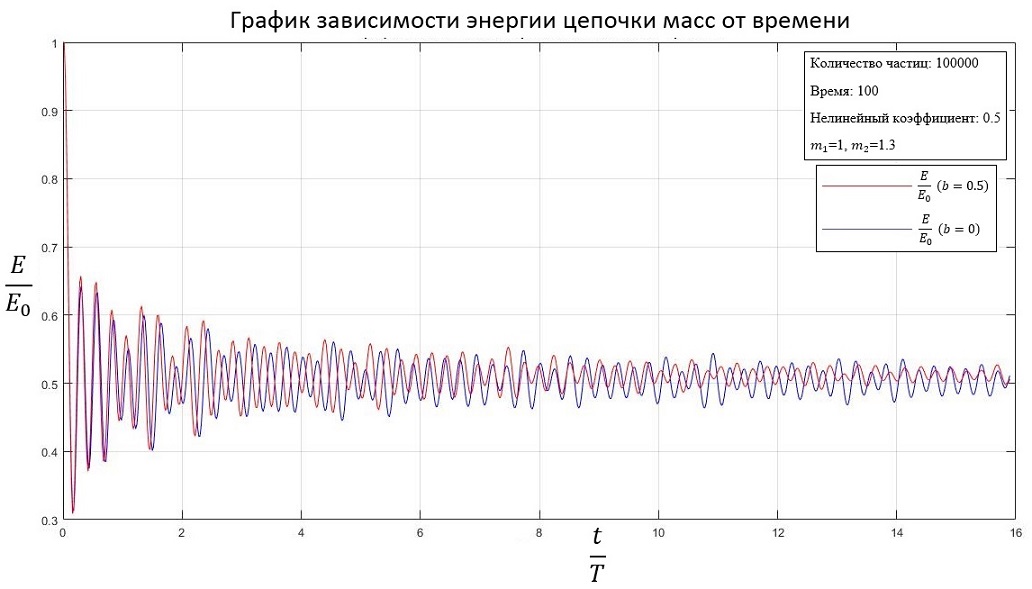
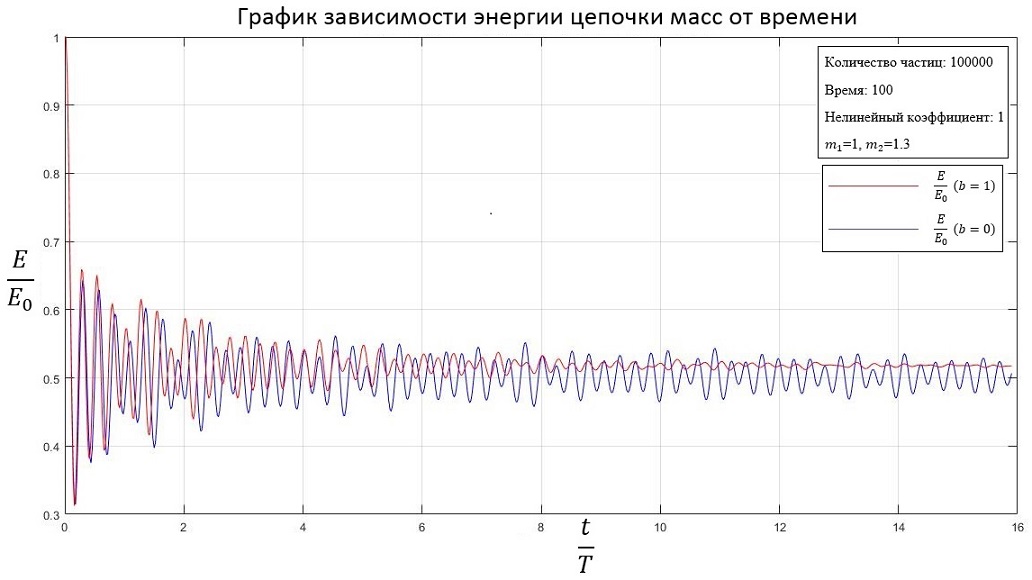
Разные массы частиц ( и ):
b=0.01
b=0.1
b=0.5
b=1
Выводы[править]
Таким образом, в ходе реализации данной работы можно сделать следующие выводы:
1. Для линейной системы с равными массами частиц график распределения кинетической энергии совпадает с функцией Бесселя нулевого порядка;
2. Для нелинейной системы с увеличением коэффициента нелинейности кинетическая энергия стабилизируется на большем значении, чем для линейной системы.