Нелинейные колебательные системы — различия между версиями
Loban9614 (обсуждение | вклад) (→Результаты работы программы) |
Loban9614 (обсуждение | вклад) (→Список литературы) |
||
| Строка 49: | Строка 49: | ||
[[File:Рисунок4.png]] | [[File:Рисунок4.png]] | ||
| + | |||
| + | ==Выводы== | ||
| + | |||
| + | У уравнения одна особая точка (0,0). Поведение вблизи неё определяется знаком ƛ. | ||
| + | В случае начального положения, удалённого от особой точки, при ƛ=0 и различных малых µ движение системы с течением времени стремится к гармоническим колебаниям | ||
| + | |||
==Список литературы== | ==Список литературы== | ||
| Строка 58: | Строка 64: | ||
| + | ==Ссылки== | ||
| − | + | '''Презентация''' | |
| − | ''' | ||
[[:File:Нелинейные колебательные системы.pptx]] | [[:File:Нелинейные колебательные системы.pptx]] | ||
| − | '''Код''' | + | '''Код программы''' |
[[:File:lab5_diff_eq.rar]] | [[:File:lab5_diff_eq.rar]] | ||
Версия 12:00, 2 июня 2017
Курсовой проект по информатике
Исполнитель: Лобанов Илья Юрьевич
Группа: 23604/1
Содержание
Аннотация к проекту
Дано нелинейное дифференциальное уравнение 2-ого порядка: 𝑥 ̈- (ƛ + µ𝑥^(2 )- 𝑥^4)𝑥 ̇ ẍ - (ƛ + µx^2). Необходимо исследовать поведение решения при различных малых значениях ƛ и µ.
Постановка задачи
- Преобразовать данное уравнение к системе из 2-х ОДУ 1-го порядка в фазовом пространстве
- Отыскать особые точки системы
- Линеаризовать систему в окрестности особых точек
- Определить типы особых точек и поведение решения вблизи этих точек
- Численно решенить данное уравнение с помощью метода Рунге-Кутта 4-го порядка
Описание работы программы
Программа написана c помощью пакета прикладных программ Matlab. С помощью метода Рунге-Кутта 4-го порядка в программе численно находятся значения исследуемого уравнения.Затем программа выводит графики решений данного уравнения и фазовые траектории в зависимости от заданных в функции Calculate начальных условий.
Результаты работы программы
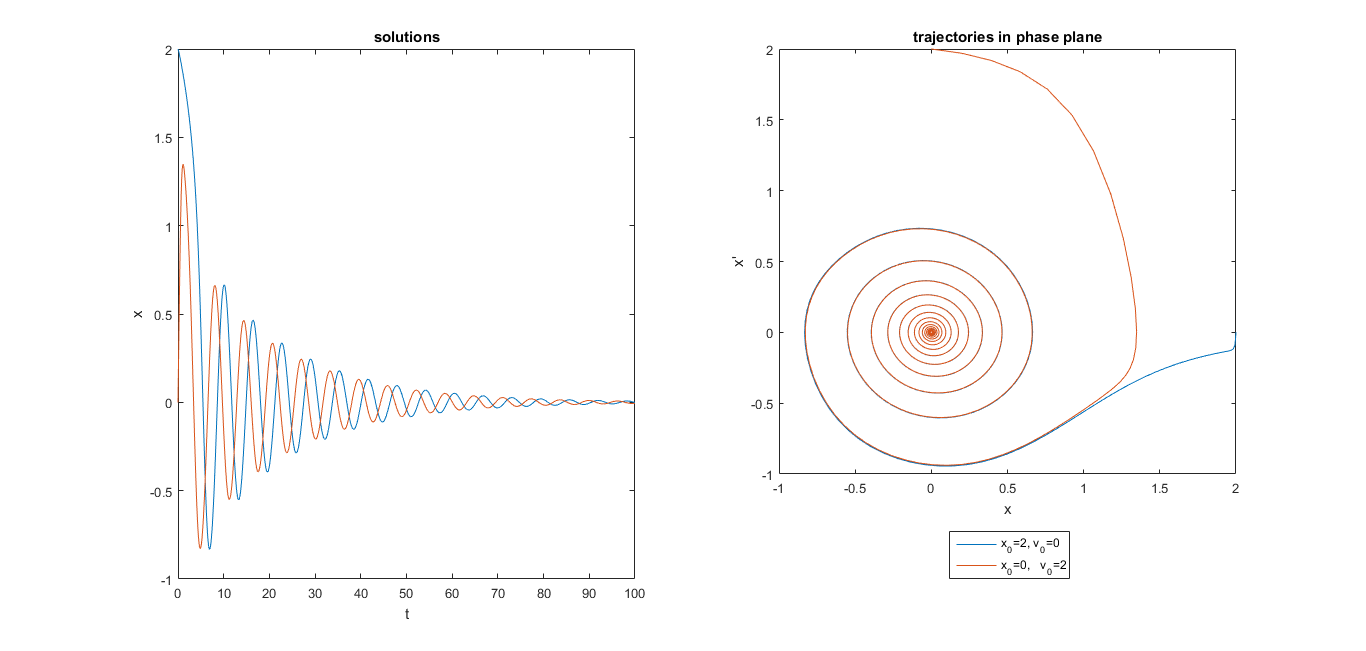
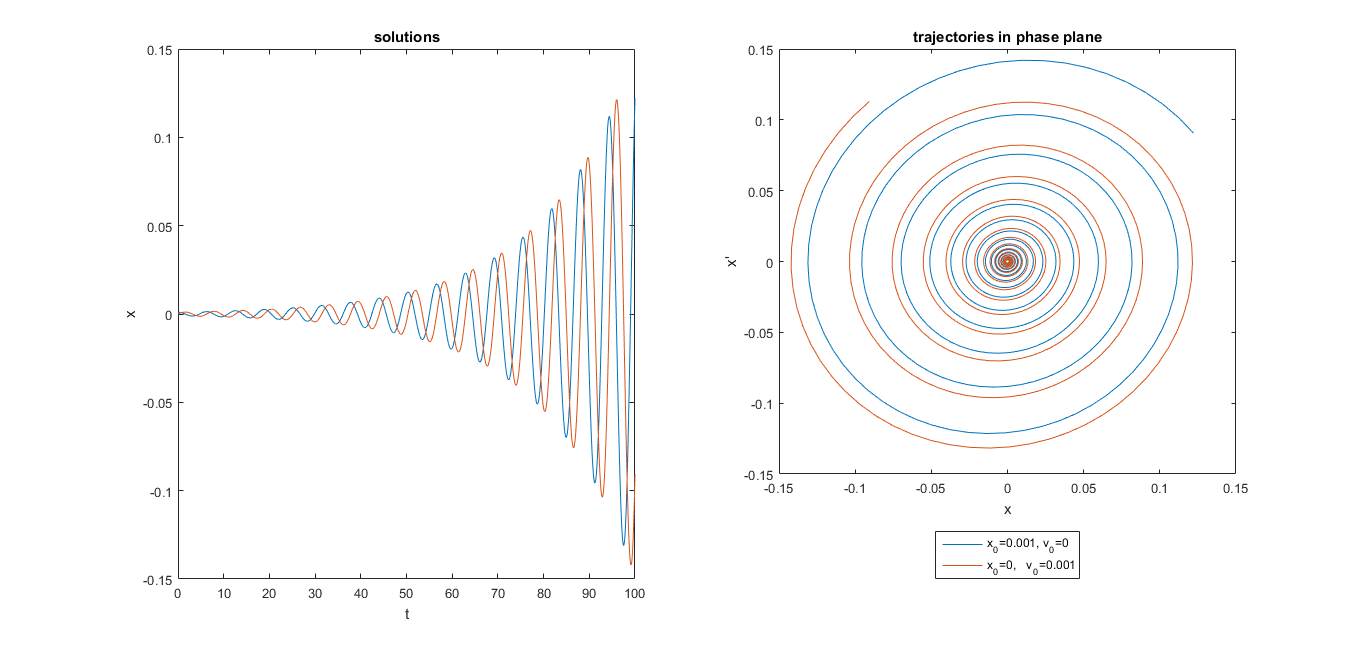
ƛ=-0.1, µ=0 , вблизи особой точки
ƛ=0.1, µ=0 , вблизи особой точки
ƛ=0, µ=0 , вблизи особой точки
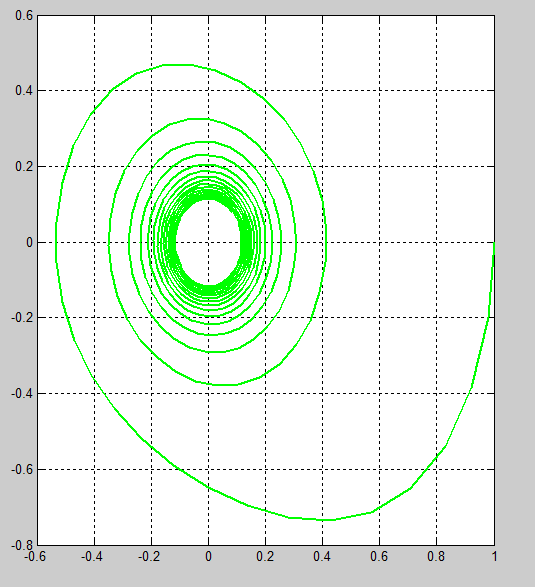
ƛ=0, µ=0 , начальное положение удалено особой точки
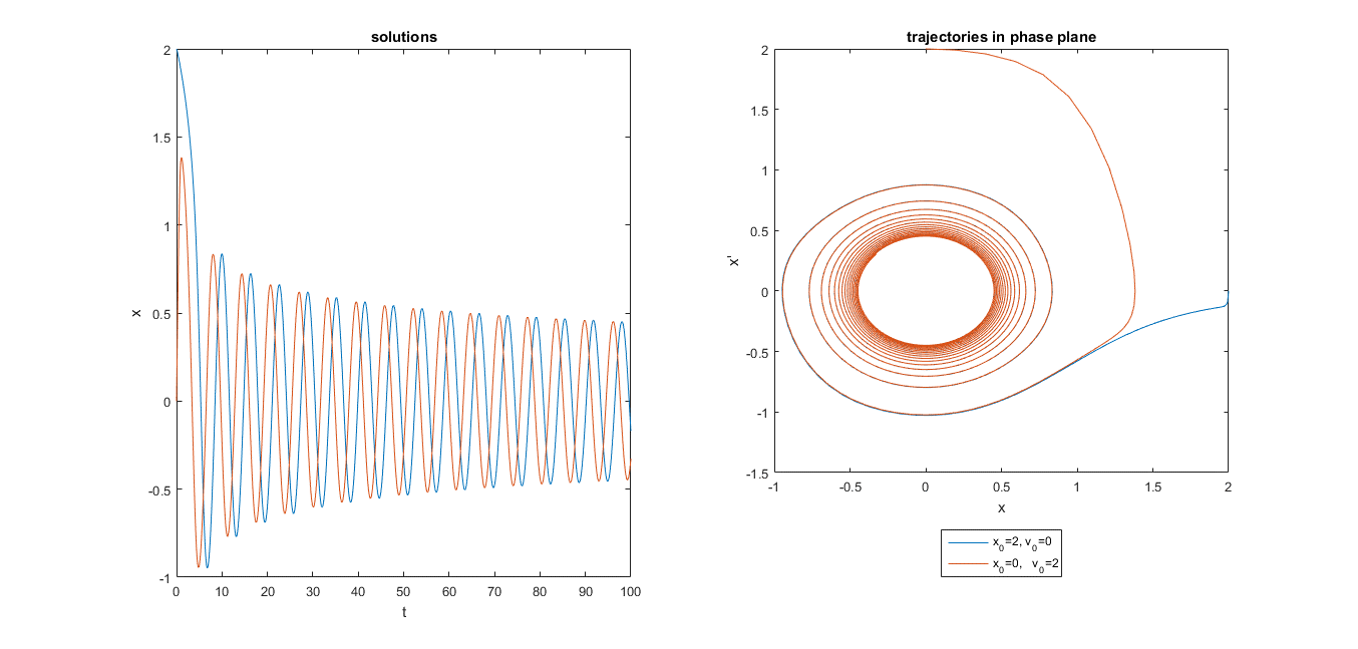
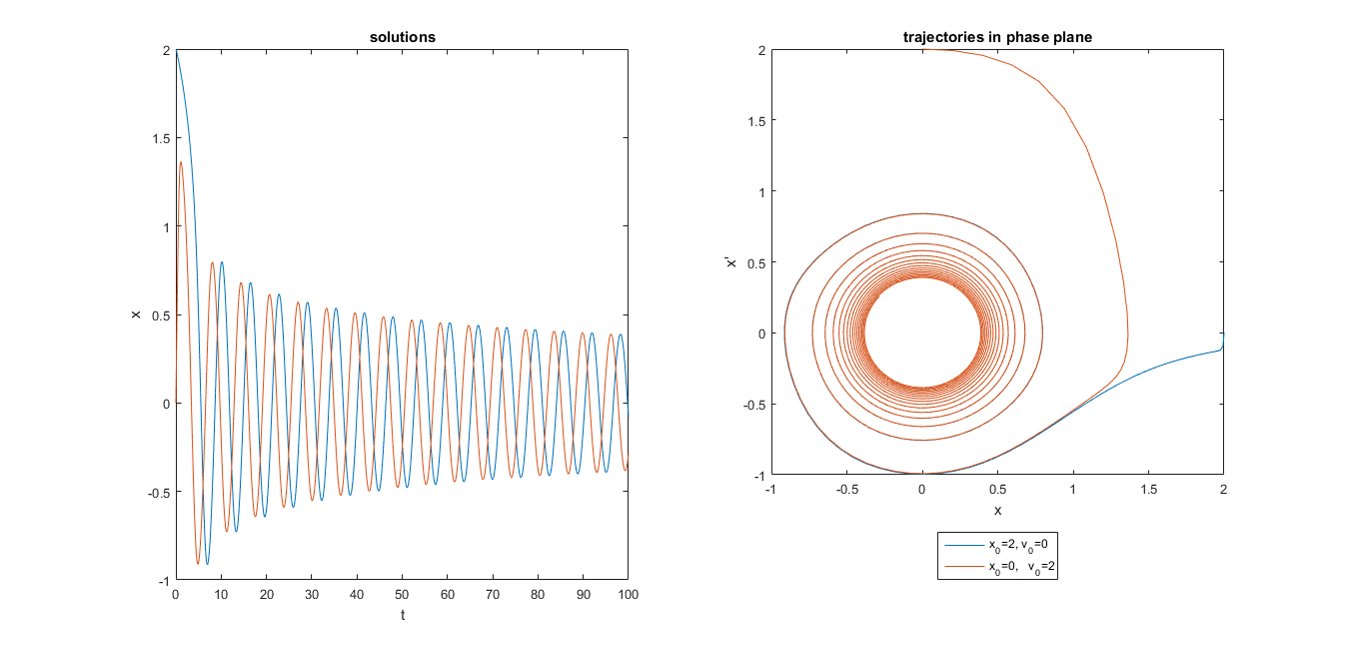
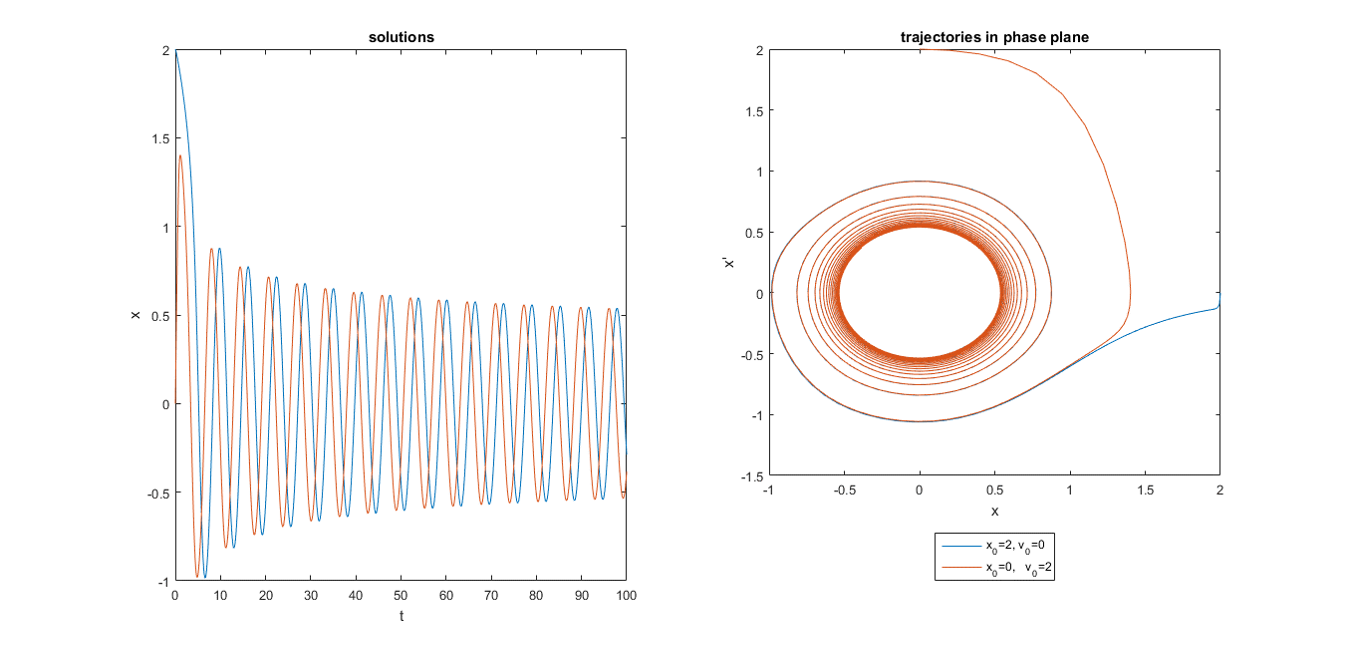
ƛ=0, µ=-0.1, начальное положение удалено особой точки
ƛ=0, µ=0.1, начальное положение удалено особой точки
Выводы
У уравнения одна особая точка (0,0). Поведение вблизи неё определяется знаком ƛ. В случае начального положения, удалённого от особой точки, при ƛ=0 и различных малых µ движение системы с течением времени стремится к гармоническим колебаниям
Список литературы
- Алдошин Г.Т. Теория линейных и нелинейных колебаний:Учебное пособие. 2-е изд., стер.
Ссылки
Презентация File:Нелинейные колебательные системы.pptx Код программы File:lab5_diff_eq.rar