Модель Скотта

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск

Модель Скотта - это механическая система, которая служит для демонстрации солитонных решений уравнения sin-Гордона (Френкеля-Конторовой) вида: [math]\ddot{u} - u'' = -\sin u[/math]

Участники проекта

Обновленная версия установки, выполненная в рамках 3-ей Школы Fab Lab

Александр Гаврилов (электроника)

Катерина Чижкова (программирование)

Ольга Костенко (механика)

Сергей Сычугов (электроника)

Михаил Бабенков (механика, автор проекта)

Краткие исторические сведения

John Scott Russell (1808-1882)

Уединенные волны (солитоны) впервые стали предметом научных исследований в 1834 году благодаря английскому инженеру Джону Скотту Расселу, проводившему судоходные эксперименты в канале Юнион, недалеко от Эдинбурга. В своих трудах он описал увиденное им явление так:

"... масса воды... собралась около носа судна... затем неожиданно оставила его позади, катясь вперед с огромной скоростью и принимая форму большого одиночного возвышения, т.е. округлого, гладкого и четко выраженного водяного холма, который продолжал свой путь вдоль канала, ни сколько не меняя своей формы и не снижая скорости..." [1]

Нелинейное дифференциальное уравнение в частных производных, которое является математическим описанием "гидродинамической уединеной волны Рассела" или "солитона Рассела" было получено лишь около 60 лет спустя, в 1895 году Дидериком Кортевегом и Густавом де Вризом.

Второе рождение уединенные волны пережили в 1965 году, когда исследователи М. Крускал и Н. Забуски, проведя численный эксперимент, установили, что нелинейная волна обладает свойствами, характерными скорее для частиц. Выяснилось, что уединенные волны не проходят друг через друга (как это считалось во времена Рассела), а отталкиваются подобно упругим телам. Название "уединенная волна" было немедленно заменено термином "солитон", созвучным с названием элементарных частиц.

Парадоксально, что способность проявлять свойства как упругих тел так и волн сначала были установлены у объектов настолько малых размеров, что наблюдать их можно было лишь косвенно, и только затем, спустя почти пол века, обнаружены у объектов макро мира.

Стоит заметить, что солитонные решения инвариантны относительно преобразования Лоренца [2], из этого следует, что при приближении скорости солитона к скорости звука в среде, он испытывает сокращение своих размеров в направлении движения. В специальной теории относительности (СТО) аналогичный эффект называется "сокращение Лоренца" и вместо скорости звука в среде фигурирует скорость света в вакууме.

Виды солитонов (уединенных нелинейных волн)

Свойства линейных волн:

  • скорость всех линейных волн одинакова и зависит только от свойств среды
  • частота, скорость и длина линейных волн связаны простым соотношением [math]\omega = c/\lambda[/math]
  • линейные волны свободно проходят друг через друга, образуя интерференционную картину

Некоторые виды нелинейных волн и их свойства [2], [3]:

  • стоячие волны - не двигаются, совершая колебания на одном месте; частота таких колебаний должна быть отстроена от собственных частот системы
  • кинки и антикинки - топологические солитоны, различающиеся разным направление закрученности; взаимоуничтожаются при столкновении "кинк-антикинк" как частицы с разноименными зарядами и отталкиваются как упругие тела при взаимодействии типа "кинк-кинк", скорость кинка зависит от его размера
  • бризеры - могут как стоять на месте, так и двигаться; представляют собой повторяющийся процесс рождения-взаимоуничтожения кинка и анитикинка; частота этого периодического процесса должна быть отстроена от собственных частот системы
  • тахионы - перемещаются быстрее скорости распространения линейных волн в среде (так же называются гипотетические элементарные частицы, перемещающиеся со скоростью превышающей скорость света)

Разнообразие солитонных явлений [2]: Цунами, сверхвысокие волны (т.н. "фрики", от англ. freaks), нервные импульсы, распространения света в оптических волокнах, локальные колебания в молекулах и молекулярных кристаллах, динамика Большого Красного Пятна на Юпитере и т.д.

Уединенные волны наблюдаются в решениях следующих нелинейных дифференциальных уравнений: Кордевега де Вриза (описывает распространение солитона Рассела), нелинейного уравнения Шрёдингера (описывает распространение волновых пакетов на большой глубине), sin-Гордона (данное уравнение подробно рассматривается ниже). С этими и некоторыми другими уравнениями можно ознакомиться в книге [2].

Уравнение sin-Гордона

Данное уравнение применяется для описания следующих процессов [2], [3]:

  • перемещений дислокаций (ячейки кристаллической решетки с отсутствующим атомом) в кристаллах, взаимодействие дислокаций и антидислокаций (ячеек с лишним атомом) [4]
  • моделирования элементарных частиц [5]
  • расплетания цепочки ДНК при репликации и динамики протяженных молекул [6], [4]
  • распространения поперечных электромагнитных волн в длинном полосковом волноводе (полосковый волновод представляет собой слой диэлектрика, заключенный между двумя сверхпроводниками, через который протекает сверхпроводящий ток; данное явление известно под названием "эффект Джозефсона") [7]
  • распространения границ доменов (доменом называется макроскопическая область намагниченности в материале) ферромагнитных и ферроэлектрических материалов [4]

Экспериментальная установка

ЦТТМ > Фаблаб Политех > Проекты Фаблаб Политех > Модель Скотта

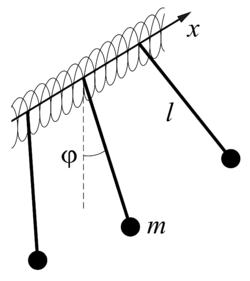
Уравнение sin-Гордона имеет простую механическую интерпретацию. Модель Скотта (Рис. 1) представляет из себя маятниковую решетку, в которой распространяются крутильные волны [8].

Рис. 1 Фотография установки

Длина установки составляет 1.1м, 60 маятников длиной 12см закреплены с помощью деревянных цилиндров толщиной около 1см на пружине с шагом 5мм, навитой из проволоки ГОСТ 9389-75 (диаметр 0.7мм). Диаметр цилиндров подогнан под внутренний диаметр пружины. Цилиндры вращаются вокруг струны натянутой между кронштейнами.

Для изготовления установки использовалось оборудование Мини Фаблаб.

16 марта 2013г., в клубе YES™ состоялась итоговая лекция с демонстрацией работы установки.

Вывод уравнения динамики механической системы

Рис. 2 Схематическое изображение модели

Маятники связаны пружинами с жесткостью [math]\kappa[/math], работающими на кручение (Рис. 2). Масса каждого маятника равна [math]m[/math], его момент инерции находится по формуле [math]m l^2[/math], где [math]l[/math] - длина маятника. Расстояние между маятниками на оси [math]x[/math] равно [math]d[/math].

Если отклонить [math]i[/math]-ый маятник из положения равновесия на угол [math]\varphi_i[/math], то на него будут действовать момент силы тяжести [math]-mgl \sin \varphi_i[/math], момент со стороны предыдущей пружины [math]-\kappa(\varphi_i-\varphi_{i-1})[/math] и момент со стороны следующей за ним пружины [math]-\kappa(\varphi_i-\varphi_{i+1})[/math], тогда систему разностных уравнений движения дискретной маятниковой системы можно записать так:

[math]m l^2 \ddot{\varphi_i} = -mgl \sin \varphi_i -\kappa(\varphi_i-\varphi_{i+1})-\kappa(\varphi_i-\varphi_{i-1})[/math]

Или:

[math]m l^2 \ddot{\varphi_i} = -mgl \sin \varphi_i +\kappa(\varphi_{i+1} -2\varphi_i +\varphi_{i-1})[/math]

Перепишем в новых обозначениях:

[math]\ddot{\varphi_i} - c^2 \frac{\varphi_{i+1} -2\varphi_i +\varphi_{i-1}}{d^2} = -\Omega^2 \sin \varphi_i[/math]

Где [math]c^2=\frac{\kappa d^2}{m l^2}[/math], [math]\Omega^2=\frac{g}{l}[/math]

Для перехода к континуальной модели воспользуемся длинноволновым приближением, т.е. будем рассматривать волны, длина которых много больше расстояния между маятниками. Тогда, согласно определению производной, дробь [math](\varphi_{i+1} -2\varphi_i +\varphi_{i-1})/(d^2)[/math] можно заменить операцией дифференцирования по координате [math]x[/math]:

[math]\ddot{\varphi} - c^2 \varphi '' = - \Omega^2 \sin \varphi[/math]

Где [math]c[/math] - скорость распространения линейных волн (волн с малой амплитудой) в среде.

Полученное уравнение называется уравнением sin-Гордона.

Точные решения уравнения sin-Гордона (СГ) получаются с помощью преобразования Бэклунда. В книге [2] приводятся аналитические решения для распространения одиночного СГ-солитона (кинка), взаимодействия двух однонаправленных кинков и кинк-антикинк аннигиляции.

Линеаризованное уравнение sin-Гордона (уравнение Клейна-Гордона) при малых значений угла [math]\varphi[/math] описывает колебания тяжелой нити, лежащей на упругой подложке.

Видео эксперимента

Фото и видео съемка: Андрей Голубчиков, Фотомеханика™

На видео представлены:

  • линейные волны малой амплитуды
  • отталкивание (упругое взаимодействие) двух кинков
  • аннигиляция кинка и антикинка с выделением энергии в виде линейных волн
  • кинк, увеличивающий свои размеры при уменьшении скорости за счет "сокращения Лоренца"
  • рождение двух разноименных кинков
  • отражение кинка от заделки без смены "знака" (направления закрученности)
  • отражение от свободного конца, происходящее со сменой "знака"

Стоячие волны не возникают в механической модели, так как соответствующее решение уравнения sin-Гордона получается при "нефизичных" граничных условиях нулевых угловых деформаций [2].

Обсуждение

Необычайная схожесть солитонов с объектами микромира порождает ряд интересных дискуссий, в т.ч. о природе электрического заряда [3]. Способностям отталкиваться или аннигилировать СГ-солитон обязан своим топологическим свойствам: в зависимости от направления его закрученности ему можно сопоставить положительный или отрицательный "заряд".

Топология изучает объекты безотносительно их непрерывных деформаций (таких деформаций, которые происходят без разрывов и склеиваний), т.е. геометрические тела "кружка" и "бублик" с точки зрения топологии могут рассматриваться как идентичные (топологически гомеоморфные) объекты: wiki.

Чтобы нагляднее представить как устроен СГ-солитон с точки зрения топологии, рассмотрим "солитон Эйлера", представляющий собой петлю на тонкой проволоке. Он топологически гомеоморфен кинкам в механической модели sin-Гордона (может быть получен из СГ-солитона путем непрерывных деформаций) и описывается почти тем же уравнением, что и СГ-солитон, но с той лишь разницей, что пространственную координату [math]x[/math] и время [math]t[/math] нужно поменять местами [3]. Две петли на проволоке, закрученные в одном направление "отталкиваются", если пытаться их сблизить и, ноборот, петли, закрученные в разные стороны при взаимодействии "распутывают" друг друга.

Согласно одной из гипотез, заряженные элементарные частицы обладают своими свойствами благодаря тому, что топологически гомеоморфны рассмотренным объектам.

Благодарности

Работа выполнена Михаилом Бабенковым в рамках сотрудничества с клубом YES™. Автор благодарен Андрею Мурачеву и Игорю Асонову, кафедра Теоретическая механика за предоставленную возможность поучаствовать в проекте.

Автор выражает глубокую благодарность Андрею Голубчикову, Фотомеханика™ за профессиональную фото и видео съемку.

Автор благодарен сотрудникам Мини Фаблаб, ООО «Фотомеханика» за помощь в освоении оборудования, необходимого для работы.

Список литературы

  1. ↑ Russel, J.S.: Report on Waves, 14th meeting of the British Asossiation for the Advancement of Science (1844)
  2. ↑ 2,0 2,1 2,2 2,3 2,4 2,5 2,6 Скотт, Э.: Нелинейная наука: развитие и рождение когерентных структур (перевод с англ.), Физматлит, Москва (2007)
  3. ↑ 3,0 3,1 3,2 3,3 Filippov, A.T.: The Versatile Soliton, Springer, Berlin (2000)
  4. ↑ 4,0 4,1 4,2 Кившарь, Ю.С., Браун, О.М.: Модель Френкеля-Конторовой. Концепции, методы, приложения (перевод с англ.), Физматлит, Москва (2005)
  5. ↑ Caudrey, P.J., Eilbeck, J.C., Gibbon, J.D.: The sine-Gordon equation as a model classical field theory, Il Nuovo Cimento B Series 25(2), 497-512 (1975)
  6. ↑ Давыдов, А.С.: Солитоны в квазиодномерных молекулярных структурах, УФН 138, 603–643 (1982)
  7. ↑ Josephson, B.D.: Possible new effects in superconductive tunnelling, Phys. Lett. 1(7), 251—253 (1962)
  8. ↑ Scott, A.C.: A Nonlinear Klein-Gordon Equation, American Journal of Physics 37(1), 52-61 (1969)
Источник — «http://tm.spbstu.ru/?title=Модель_Скотта&oldid=26122»