Моделирование распространения колебаний в бесконечном теле методом конечных элементов
БАКАЛАВРСКАЯ РАБОТА
Автор работы: В. С. Погодина
Руководитель: ассистент кафедры ТМ С. А. Ле-Захаров
Содержание
Введение[править]
Задачи геологоразведки, прогнозирование техногенной взрывной волны, расчет зданий и сооружений на действие сейсмических волн и другие динамические задачи распространения волн в твердом теле в настоящее время весьма актуальны. Целью данной работы является исследование распространения волн, возникающих под действием постоянной точечной силы, в бесконечных телах.В связи с поставленной целью в работе решаются следующие задачи:
- описать основные методы моделирования «бесконечных» границ
- выбрать подходящий способ моделирования «бесконечной» границы для одномерного и двумерного тела
- провести моделирование распространения волн в бесконечном одномерном и двумерном телах с помощью выбранных способов моделирования «бесконечных» границ
- проанализировать полученные результаты
Моделирование фиктивной неотражающей границы[править]
Существует несколько подходов к решению задачи моделирования поглощающей границы. Здесь рассматриваются два основных: вязкие и вязкоупругие граничные условия.
Вязкие граничные условия[править]
В однородных изотропных средах существует два типа волн:продольные и поперечные. Их скорости соответственно равны.
где - модуль сдвига, а - упругая константа, найденная по формуле:
где \mu - коэффициент Пуассона. Вязкие граничные условия задаются в соответствии с формулами, предложенными J. Lysmer и R. Kuhlemeyer:
Вязкие граничные условия в точности передают все нормально набегающие плоские волны тела. Для тех случаев, когда не удается добиться поглощения волны, используются вязкоупругие граничные условия.
Вязкоупругие граничные условия[править]
Исходя из названия вязкоупругих граничных условий, очевидно, что они имеют вязкую и упругую составляющую. Данная модель приведена в работе Андервуда и Гирса. Вязкая состовляющая задается как для вязких граничных условий.Упругая составляющая напряжений в граничных условиях задается исходя из решения стационарной задачи для достаточно большой области с тем же типом нагрузки, что и в динамической задаче.
Таким образом уравнения на границе примут следующий вид:
Одномерная задача[править]
Задача распространения колебаний в бесконечном теле может быть решена в одномерной, двумерной или трехмерной постановке. Изучение волн начнем с простейшего случая одномерного движения среды, когда все характеристики волны зависят от одной декартовой координаты, например координаты х. В данной работе исследуется поведение среды в случае точечной постоянной силы.
Постановка задачи[править]
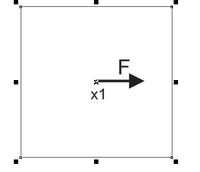
Имеется бесконечный стержень.Перемещения во всех точках этой прямой в начальный момент времени равны нулю.Начиная с момента времени, не равного нулю, в некоторой точке (х1) начинает действовать постоянная, сонаправленная с прямой сила F.Требуется найти зависимость перемещения от времени в любой точке прямой, в которой не приложена сила.Поглощающая граница создана с помощью вязких граничных условий.
Результаты численного моделирования[править]
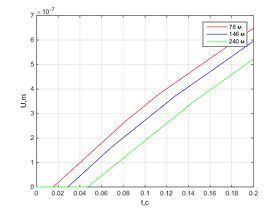
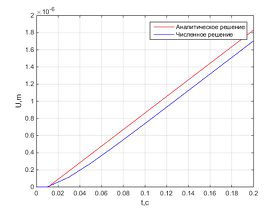
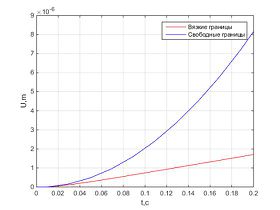
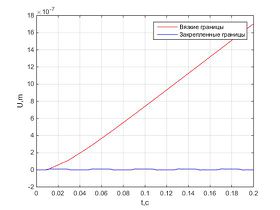
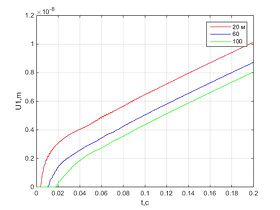
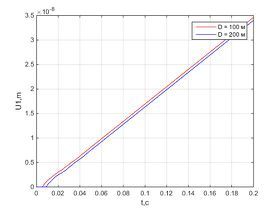
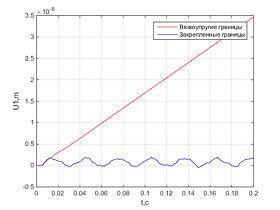
Было проведено численное решение и получены следующие результаты.Графики перемещения в разных точках стержня параллельны и отличаются лишь на длину участка, где перемещения нулевые.Численное решение незначительно отличается от аналитического, и ошибка не растет с течением времени.При использовании вязких граничных условий характер зависимости перемещения от времени линейный для всех точек стержня, в то время как для закрепленного стержня график перемещения колеблется возле некоторого значения, а для стержня со свободными границами – экспоненциально возрастает с течением времени.
Двумерная задача[править]
Продолжим изучение волн с двумерного движения среды, когда все характеристики волны зависят от двух декартовых координат, например координаты х и у. В этом случае возникают два типа волн: продольные и поперечные. В этом случае мы сталкиваемся с проблемой задания таких граничных условий, которые поглощают эти два типа волн, а именно с вязкоупругими граничными условиями.
Постановка задачи[править]
Имеется бесконечная плоскость.Начальные и граничные условия аналогичны одномерной задаче с отличием лишь в том, что они формулируются для двумерного случая. Перемещения во всех точках этой плоскости в начальный момент времени равны нулю. Начиная с момента времени, не равного нулю, в некоторой точке (х1) начинает действовать постоянная, сонаправленная, например, с осью абсцисс сила F. Требуется найти зависимость перемещения от времени в любой точке плоскости, в которой не приложена сила.
Результаты моделирования[править]
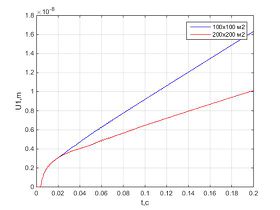
Было проведено численное моделирование и получены следующие результаты.Вязкие границы, реализованные с помощью «бесконечных» элементов или демпферов, не могут быть использованы для моделирования поглощающих границ, так как не поглощают весь спектр волн.Большое влияние на способность вязких границ проводить волны оказывает угол падения волны на границу.Вязкоупругие границы, реализованные с помощью демпферов и пружинок, чувствительны к воздействиям всего спектра частот, поэтому хорошо проводят волны на бесконечность.
Выводы[править]
В связи с отсутствием универсальных методов моделирования бесконечных тел, актуальной является задача исследования основных методов моделирования «бесконечной» границы.
В настоящей дипломной работе исследовалось распространение колебаний в бесконечном теле, возникающих в результате точечной постоянной силы. В ходе исследования были решены следующие задачи.
Были описаны два основных типа поглощающих границ: вязкие и вязкоупругие. Вязкоупругие граничные условия отличает от вязких то, что помимо вязкой составляющей они имеют еще и упругую. При этом поглощающая способность вязкоупругих граничных условий выше, за счет того, что они способны работать с волнами, которые набегают не только под прямыми углами.
Было проведено численное моделирование распространения волны в стержне. Роль поглощающих границ выполняли вязкие граничные условия, с помощью которых удалось добиться согласия численного и аналитического решения.
Было также проведено моделирование распространения колебаний в пластине. Вязкие граничные условия были реализованы как с помощью «бесконечных» элементов, так и с помощью демпферов на границе. При использовании вязких граничных условий не удалось добиться поглощения волны на границе.
Поэтому была создана численная модель, реализующая вязкоупругие граничные условия. Демпферы и пружинки на границе создавались программой, написанной на языке программирования Python, коэффициенты вязкости и упругости которых задавались исходя из решения стационарной задачи. При использовании вязкоупругих граничных условий удалось добиться поглощения волны на границе.
В дальнейшем исследование планируется расширить за счет использования других методов моделирования «бесконечной» границы и других типов прикладываемой нагрузки.
Литература[править]
- Тропкин С. Н., Тляшева Р. Р., Баязитов М. И., Разработка Защитного Устройства Операторной Станции при Воздействии Воздушной Взрывной Волны с Помощью Программного Комплекса Abaqus // «ООО ТЕСИС»
- Терентьева Е.О. Задача Лэмба [Электронный ресурс] // Строительство: наука и образование. 2013. Вып. 3. Ст. 3. Режим доступа: http://www.nso-journal.ru.
- Расчет сооружений на сейсмические воздействия и ветровую нагрузку с пульсационной составляющей : учеб. пособие /А. Н. Куликов ; Волгогр. гос. архит.-строит. ун-т ; Волж. ин-т стр-ва и технол. (филиал) ВолгГАСУ.–Волгоград: ВолгГАСУ, 2008.–91 с.
- Галлагер Р. Метод конечных элементов. Основы: Пер. с англ. — М.: Мир, 1984
- Деклу Ж. Метод конечных элементов: Пер. с франц. — М.: Мир, 1976
- Зенкевич О. Метод конечных элементов в технике — М.: Мир, 1975.
- Ильгамов М. А., Гильманов А. Н. Неотражающие условия на границах расчетной области. — М.: ФИЗМАТЛИТ, 2003. — 240 с.
- Lysmer J., Kuhlemeyer R. L., Finite dynamic model for infinite media // Journal of the Engineering Mechanics Division, Berkeley, 1969, pp. 859-877.
- Underwood P., Geers T. L. Doubly Asymptomic Boundary-Element Analysis of Dynamic Soil-Structure interaction // International Journal of Solids and Structures, 1981, n. 17, pp. 687-697.
- Abaqus 6.13 Documentation. Доступно по ссылке: http://129.97.46.200:2080/v6.13/books/usb/default.htm?startat=pt06ch32s02ael27.html