Задача: С помощью языка программирования JavaScript смоделировать эллиптический маятник.
Исполнитель: Серов Александр
Группа: 23632/2
Семестр: осень 2017
Решение
Используемые библиотеки
- three.js
- dat.gui.js
- reflector.js
- orbitControls.js
Возможности программы
- изменение масс шара, катушки и веревки
- детальное рассмотрение работы с удобного ракурса
Решение частного случая
Условия задачи:
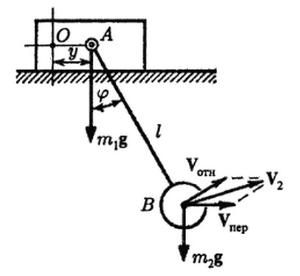
Определить движение груза массы m, висящего на однородном тросе массы m1 и длины l; трос навернут на барабан радиуса a и массы m2; ось вращения горизонтальна; трением пренебречь, массу барабана считать равномерно распределенной по его ободу. В начальный момент t=0 система находилась в покое, длина свисавшей части троса l0.
Решение:
[math]\frac{d}{dt}\left(\frac{\partial L}{\partial\dot q_i}\right) - \frac{\partial L}{\partial q_i} = 0 [/math]
где [math]L[/math] - функция Лагранжа
[math]L = T-\Pi [/math]
[math]T[/math] - кинетическая энергия системы, [math]\Pi[/math] - потенциальная энергия системы [math]q_1 = y[/math] , [math]q_2 = \varphi [/math]
[math]T = T_1 + T_2[/math], где [math] T_1[/math] - кинетическая энергия ползуна, [math]T_1[/math] - кинетическая энергия шара
[math]T_1 = \frac{1}{2}\ m_1\dot y^{2}[/math]
[math]T_2 = \frac{1}{2}\ m_2\ V_2 ^{2}[/math]
[math]V_2 = V_e + V_r[/math] , [math]V_e = \dot \varphi \ l[/math] , [math]V_r = \dot y\[/math]
[math]V_2 ^{2} = \dot y^{2}\ + \dot \varphi ^{2}\ l^{2} + 2\ l\dot y\dot \varphi \cos(\varphi )\[/math]
[math]T = \frac{1}{2} \ (m_1 + m_2) \dot y^{2} + \frac{1}{2} \ m_2 \ l ^{2} \dot \varphi^{2} + m_2 \ l\dot y\dot \varphi \cos(\varphi )\[/math]
[math]\Pi = - m_2 \ l\ g \cos(\varphi )\ [/math]
[math]L = \frac{1}{2} \ (m_1 + m_2) \dot y^{2} + \frac{1}{2} \ m_2 \ l ^{2} \dot \varphi^{2} + m_2 \ l\ (\dot y\dot \varphi + g) \cos(\varphi )\[/math]
[math]\frac{\partial L}{\partial\dot y} = (m_1 + m_2) \dot y + m_2 \ l\dot \varphi \cos(\varphi )\[/math]
[math]\frac{\partial L}{\partial y} = 0 [/math]
[math]\frac{\partial L}{\partial\dot \varphi } = m_2 \ l ^{2} \dot \varphi + m_2 \ l\dot y \cos(\varphi )\[/math]
[math]\frac{\partial L}{\partial\varphi} = - m_2 \ l\ (\dot y\dot \varphi + g) \sin(\varphi )\[/math]
В результате получаем уравнения , описывающие движение рассматриваемой системы :
[math] (m_1 + m_2) \ddot y + m_2 \ l\ddot \varphi \cos(\varphi ) - m_2 \ l\dot \varphi \sin(\varphi ) = 0[/math]
[math] l \ddot \varphi + \ddot y \cos(\varphi ) + g \sin(\varphi) = 0 [/math]
См. также