КП: Динамика несферических гравитирующих тел — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
(→‎Обсуждение результатов и выводы)
 
(не показаны 4 промежуточные версии 1 участника)
Строка 12: Строка 12:
 
== Аннотация проекта ==
 
== Аннотация проекта ==
 
Данный проект посвящён динамике несферических гравитирующих тел.  
 
Данный проект посвящён динамике несферических гравитирующих тел.  
 +
На первом этапе одна из частиц считается неподвижной и рассматривается как материальная точка. На следующем этапе планируется рассмотреть обе частицы как несферические тела, которые вращаются вокруг неподвижной точки.
 
Тела, не обладающие сферической симметрией, интересны тем, что их сила притяжения отличается от классического закона всемирного тяготения на асимптотически главный член.  
 
Тела, не обладающие сферической симметрией, интересны тем, что их сила притяжения отличается от классического закона всемирного тяготения на асимптотически главный член.  
  
 
== Постановка задачи ==
 
== Постановка задачи ==
−
[[Файл:20133.png]]
+
[[Файл:787.png]]
  
 
Даны два несферических тела, а именно две гантели. Для выполнения первого этапа нужно считать одну из гантелей неподвижной и рассматривать её как материальную точку. Из неё проводится радиус-вектор <math>\vec{r}</math> в центр масс второй частицы.  
 
Даны два несферических тела, а именно две гантели. Для выполнения первого этапа нужно считать одну из гантелей неподвижной и рассматривать её как материальную точку. Из неё проводится радиус-вектор <math>\vec{r}</math> в центр масс второй частицы.  
  
−
<math>\varphi</math> - это угол поворота, который характеризует на сколько повернулась вторая частица относительно своего изначального положения.
+
<math>\varphi</math> — это угол поворота, который характеризует на сколько повернулась вторая частица относительно своего изначального положения.
  
−
<math>M</math> - масса неподвижной частицы.
+
<math>M</math> — масса неподвижной частицы.
  
−
<math>m_{1} + m_{2}</math> - масса подвижной частицы.
+
<math>m_{1} + m_{2}</math> — масса подвижной частицы.
  
 
== Общие сведения по теме ==
 
== Общие сведения по теме ==
−
На первом этапе одна из частиц считается неподвижной и рассматривается как материальная точка. На следующем этапе планируется рассмотреть обе частицы как несферические тела, которые вращаеются вокруг неподвижной точки.
+
Примером таких систем может служить притяжение спутника и Земли, так как принцип ориентации в этих системах легко понять на примере гантели (две равные массы, соединенные жестким невесомым стержнем), центр масс которой движется по круговой орбите. Различие сил притяжения конечных масс гантели Землей приводит к появлению гравитационного момента, стремящего совместить ось гантели с направлением радиуса-вектора, соединяющего центры масс Земли и спутника. Это положение равновесия является устойчивым (случай Луны, имеющей форму слегка вытянутой дыни). Существует и неустойчивое положение равновесия, когда ось гантели совпадает с направлением касательной к орбите. Ясно, что величина управляющего гравитационного момента зависит от размеров спутника. Спутник с неравными главными центральными моментами инерции имеет на круговой орбите четыре устойчивых положения равновесия, соответствующих совпадению наибольшей оси эллипсоида инерции спутника с радиусом-вектором и наименьшей оси с нормалью к плоскости орбиты.
 +
 
 +
[[Файл:qqq.png]]
 +
 
 +
[[Файл:q.gif]]
  
 
== Решение ==
 
== Решение ==
 
Запишем силу притяжения рассматриваемой системы тел: <math>\vec{F} = \vec{F_1} + \vec{F_2}</math>.  
 
Запишем силу притяжения рассматриваемой системы тел: <math>\vec{F} = \vec{F_1} + \vec{F_2}</math>.  
  
−
Отсюда получаем после разложения в ряд Тейлора <math>\vec{F} = F_x\vec{i} + F_y\vec{j}</math>, где <math>F_x = \frac{A}{r^2} + \frac{B}{r^3}</math>, <math>F_y = \frac{C}{r^3}</math>.  
+
Отсюда получаем после разложения в ряд Тейлора <math>\vec{F} = F_x\vec{i} + F_y\vec{j}</math>, где <math>F_x = \frac{A}{r^2} + \frac{B}{r^3}</math> + остальные члены ряда, <math>F_y = \frac{C}{r^3}</math>.  
  
 
Величины <math>A,B,C</math> включают в себя массы всех тел и угол поворота подвижной частицы.
 
Величины <math>A,B,C</math> включают в себя массы всех тел и угол поворота подвижной частицы.
Строка 39: Строка 44:
 
<math>\vec{e_r} = \cos\theta\vec{i} + \sin\theta\vec{j}</math>
 
<math>\vec{e_r} = \cos\theta\vec{i} + \sin\theta\vec{j}</math>
  
−
<math>\vec{e}_\theta = \cos\theta\vec{i} + \sin\theta\vec{j}</math>
+
<math>\vec{e}_\theta = -\sin\theta\vec{i} + \cos\theta\vec{j}</math>
  
 
А тогда сила примет вид:
 
А тогда сила примет вид:
Строка 47: Строка 52:
 
Момент такой системы: <math>\vec{M} = \frac{D}{r^3}\vec{k}</math>.  
 
Момент такой системы: <math>\vec{M} = \frac{D}{r^3}\vec{k}</math>.  
  
−
Величина <math>D</math> также включают в себя массы всех тех и угол поворота подвижной частицы.
+
Величина <math>D</math> также включают в себя массы всех тел и угол поворота подвижной частицы.
  
−
Запишем <math>J</math> - момент инерции:
+
Запишем <math>J</math> — момент инерции:
  
 
<math>J = 2(m_{1} + m_{2})R^2</math>, где <math>R</math> характеризует положение центра масс подвижной частицы.   
 
<math>J = 2(m_{1} + m_{2})R^2</math>, где <math>R</math> характеризует положение центра масс подвижной частицы.   
  
−
Таким образом, можно записать систему дифференциальных уравнений, которые и будут описывать движение несферических тел в данной задачи:
+
Запишем систему дифференциальных уравнений, которые и будут описывать движение несферических тел:
  
 
<math>\begin{cases}
 
<math>\begin{cases}
  
−
(m_{1} + m_{2})\vec{\ddot{r}} = \vec{F} \\  
+
(m_{1} + m_{2})\ddot{r}_r = F_r \\
 +
 
 +
(m_{1} + m_{2})\ddot{r}_\theta = F_\theta\\
 
          
 
          
 
J\ddot{\theta} = M \\
 
J\ddot{\theta} = M \\
 
\end{cases}</math>
 
\end{cases}</math>
 +
 +
Где
  
−
Или же с учётом проекций:
+
<math>\ddot{r}_r = \dot{r} - r\dot{\theta}^2</math>
  
−
<math>\begin{cases}
+
<math>\ddot{r}_\theta = \frac{1}{r}\frac{d}{dt}(r^2\dot{\theta})</math>
 +
       
 +
<math>F_r = (\frac{A}{r^2} + \frac{B}{r^3})\cos\theta + \frac{C}{r^3}\sin\theta</math>
  
−
(m_{1} + m_{2})\ddot{r}_r = F_r \\
+
<math>F_\theta = -(\frac{A}{r^2} + \frac{B}{r^3})\sin\theta + \frac{C}{r^3}\cos\theta</math>
  
−
(m_{1} + m_{2})\ddot{r}_\theta = F_\theta \\
 
−
       
 
−
J\ddot{\theta} = M \\
 
−
\end{cases}</math>
 
−
         
 
 
== Обсуждение результатов и выводы ==
 
== Обсуждение результатов и выводы ==
−
 
+
В данной работе удалось получить уравнения, которые описывают движения тел в простом случае, то есть, когда одна частица принимается как неподвижная материальная точка, а другая частица - гантель вращается вокруг неё. Далее эту систему можно решить численно или аналитически.
  
 
== Ссылки по теме ==  
 
== Ссылки по теме ==  

Текущая версия на 14:42, 3 июня 2013

А.М. Кривцов > Теоретическая механика > Курсовые проекты 2013 > Динамика несферических гравитирующих тел


Курсовой проект по Теоретической механике

Исполнитель: Прокопенко Анастасия

Группа: 07 (20510)

Семестр: весна 2013

Аннотация проекта[править]

Данный проект посвящён динамике несферических гравитирующих тел. На первом этапе одна из частиц считается неподвижной и рассматривается как материальная точка. На следующем этапе планируется рассмотреть обе частицы как несферические тела, которые вращаются вокруг неподвижной точки. Тела, не обладающие сферической симметрией, интересны тем, что их сила притяжения отличается от классического закона всемирного тяготения на асимптотически главный член.

Постановка задачи[править]

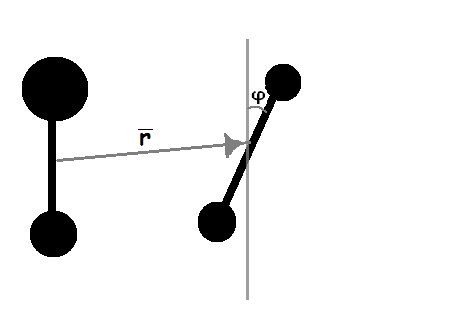
787.png

Даны два несферических тела, а именно две гантели. Для выполнения первого этапа нужно считать одну из гантелей неподвижной и рассматривать её как материальную точку. Из неё проводится радиус-вектор [math]\vec{r}[/math] в центр масс второй частицы.

[math]\varphi[/math] — это угол поворота, который характеризует на сколько повернулась вторая частица относительно своего изначального положения.

[math]M[/math] — масса неподвижной частицы.

[math]m_{1} + m_{2}[/math] — масса подвижной частицы.

Общие сведения по теме[править]

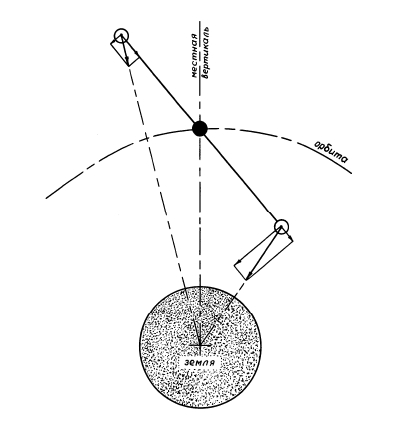
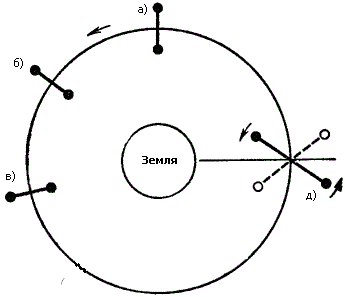
Примером таких систем может служить притяжение спутника и Земли, так как принцип ориентации в этих системах легко понять на примере гантели (две равные массы, соединенные жестким невесомым стержнем), центр масс которой движется по круговой орбите. Различие сил притяжения конечных масс гантели Землей приводит к появлению гравитационного момента, стремящего совместить ось гантели с направлением радиуса-вектора, соединяющего центры масс Земли и спутника. Это положение равновесия является устойчивым (случай Луны, имеющей форму слегка вытянутой дыни). Существует и неустойчивое положение равновесия, когда ось гантели совпадает с направлением касательной к орбите. Ясно, что величина управляющего гравитационного момента зависит от размеров спутника. Спутник с неравными главными центральными моментами инерции имеет на круговой орбите четыре устойчивых положения равновесия, соответствующих совпадению наибольшей оси эллипсоида инерции спутника с радиусом-вектором и наименьшей оси с нормалью к плоскости орбиты.

Qqq.png

Q.gif

Решение[править]

Запишем силу притяжения рассматриваемой системы тел: [math]\vec{F} = \vec{F_1} + \vec{F_2}[/math].

Отсюда получаем после разложения в ряд Тейлора [math]\vec{F} = F_x\vec{i} + F_y\vec{j}[/math], где [math]F_x = \frac{A}{r^2} + \frac{B}{r^3}[/math] + остальные члены ряда, [math]F_y = \frac{C}{r^3}[/math].

Величины [math]A,B,C[/math] включают в себя массы всех тел и угол поворота подвижной частицы.

Полученное выражение для силы нужно записать в полярных координатах. Для этого спроецируем силу на вектора:

[math]\vec{e_r} = \cos\theta\vec{i} + \sin\theta\vec{j}[/math]

[math]\vec{e}_\theta = -\sin\theta\vec{i} + \cos\theta\vec{j}[/math]

А тогда сила примет вид:

[math]\vec{F}=F_r\vec{e}_r+F_\theta\vec{e}_\theta[/math]

Момент такой системы: [math]\vec{M} = \frac{D}{r^3}\vec{k}[/math].

Величина [math]D[/math] также включают в себя массы всех тел и угол поворота подвижной частицы.

Запишем [math]J[/math] — момент инерции:

[math]J = 2(m_{1} + m_{2})R^2[/math], где [math]R[/math] характеризует положение центра масс подвижной частицы.

Запишем систему дифференциальных уравнений, которые и будут описывать движение несферических тел:

[math]\begin{cases} (m_{1} + m_{2})\ddot{r}_r = F_r \\ (m_{1} + m_{2})\ddot{r}_\theta = F_\theta\\ J\ddot{\theta} = M \\ \end{cases}[/math]

Где

[math]\ddot{r}_r = \dot{r} - r\dot{\theta}^2[/math]

[math]\ddot{r}_\theta = \frac{1}{r}\frac{d}{dt}(r^2\dot{\theta})[/math]

[math]F_r = (\frac{A}{r^2} + \frac{B}{r^3})\cos\theta + \frac{C}{r^3}\sin\theta[/math]

[math]F_\theta = -(\frac{A}{r^2} + \frac{B}{r^3})\sin\theta + \frac{C}{r^3}\cos\theta[/math]

Обсуждение результатов и выводы[править]

В данной работе удалось получить уравнения, которые описывают движения тел в простом случае, то есть, когда одна частица принимается как неподвижная материальная точка, а другая частица - гантель вращается вокруг неё. Далее эту систему можно решить численно или аналитически.

Ссылки по теме[править]

Гравитационное притяжение тел нестандартной формы

См. также[править]

Источник — «http://tm.spbstu.ru/?title=КП:_Динамика_несферических_гравитирующих_тел&oldid=19949»