КП: Динамика молекулы (расчет) — различия между версиями
Polina (обсуждение | вклад) (→Общие сведения по теме) |
Polina (обсуждение | вклад) (→Общие сведения по теме) |
||
| (не показано 15 промежуточных версий этого же участника) | |||
| Строка 11: | Строка 11: | ||
== Аннотация проекта == | == Аннотация проекта == | ||
| − | Данный проект является продолжением работы над [[Проект "Земля - Луна"]], начатый [[А.М.Кривцов]]ым и [[Ле-Захаров А.А.|А.А | + | Данный проект является продолжением работы над [[Проект "Земля - Луна"|проектом "Земля-Луна"]], начатый [[А.М.Кривцов]]ым и [[Ле-Захаров А.А.|А.А.Ле-Захаровым]]. |
| − | Исследуется поведение газопылевого облака в гравитационном поле, создаваемом Солнцем | + | Исследуется поведение газопылевого облака в гравитационном поле, создаваемом Солнцем. |
== Постановка задачи == | == Постановка задачи == | ||
| − | + | Главная задача - выполнить предварительные расчёты и теоретически предсказать результаты моделирования. | |
| + | Ранее были получены результаты для облака, имеющего форму эллипсоида. Для этого случая были проведены исследования, которые выявили наиболее оптимальные начальные данные, при которых образование двойной системы происходит с большой вероятностью, однако не было теоретически предсказано, на каком расстоянии от Земли должна образовываться Луна. | ||
== Общие сведения по теме == | == Общие сведения по теме == | ||
| Строка 33: | Строка 34: | ||
[[Файл:G-spheresOfEarth.jpg]] | [[Файл:G-spheresOfEarth.jpg]] | ||
| + | |||
| + | медиафайл взят с сайта [http://astro.uni-altai.ru/] | ||
== Решение == | == Решение == | ||
Введем общие обозначения: | Введем общие обозначения: | ||
| − | <math>k=\frac{m_{earth}}{m_{sun}}</math>, a-расстояние от Земли до Солнца. | + | <math>k=\frac{m_{earth}}{m_{sun}}</math>, <math>a</math> - расстояние от Земли до Солнца. |
*Сфера притяжения | *Сфера притяжения | ||
Ищется геометрическое место точек, в которых сила,действующая на спутник в этой точке со стороны Земли больше,чем со стороны Солнца. | Ищется геометрическое место точек, в которых сила,действующая на спутник в этой точке со стороны Земли больше,чем со стороны Солнца. | ||
| Строка 42: | Строка 45: | ||
Для Земли расстояние от центра Земли до центра сферы притяжения на несколько порядков меньше,чем радиус сферы притяжения, поэтому им можно пренебречь и считать центром сферы притяжения центр Земли. | Для Земли расстояние от центра Земли до центра сферы притяжения на несколько порядков меньше,чем радиус сферы притяжения, поэтому им можно пренебречь и считать центром сферы притяжения центр Земли. | ||
*Сфера действия | *Сфера действия | ||
| − | Привяжем систему отсчёта к Земле. Тогда ускорение спутника можно разбить на 2 составляющие: в одну в качестве коэффициента входит масса Солнца, в другую - всё остальное. Первую составляющую назовём "возмущающим" ускорением, вторую-"собственным". Отношение этих двух величин обозначим за | + | Привяжем систему отсчёта к Земле. Тогда ускорение спутника можно разбить на 2 составляющие: в одну в качестве коэффициента входит масса Солнца, в другую - всё остальное. Первую составляющую назовём "возмущающим" ускорением, вторую-"собственным". Отношение этих двух величин обозначим за <math>A</math>. Чем меньше значение <math> A </math>, тем меньше орбита спутника отличается от Кеплеровской орбиты. |
| − | Аналогичный коэффициент | + | Аналогичный коэффициент <math> B </math> можем получить,привязав СО к Солнцу. В этом случае "возмущающим" ускорением будет составляющая, в коэффициент при которой входит масса Земли. |
| − | Область,в которой | + | Область,в которой <math> A </math> < <math> B </math>, называется сферой действия Земли относительно Солнца. Геометрическим местом всех таких точек является поверхность, задаваемая уравнением в полярных координатах <math>r=\frac{ak^{0.4}}{\sqrt[10]{1+3cos^2(\theta)}}</math> |
| − | Строго говоря,эта поверхность не является сферой, а представляет собой | + | Строго говоря,эта поверхность не является сферой, а представляет собой некий эллипсоид. Однако при малых значениях k поверхность мало отличима от сферы радиусом <math>r=ak^{0.4}</math> с центром в точке, совпадающей с центром Земли. |
*Сфера Хилла | *Сфера Хилла | ||
Сфера Хилла рассчитывалась исходя из представлений о точках Лагранжа.Точки Лагранжа-это точки в системе из двух массивных тел, в которых третье тело с пренебрежимо малой массой, на которое не действуют никакие другие силы, кроме гравитационных сил со стороны двух первых тел, может оставаться неподвижным относительно этих тел. | Сфера Хилла рассчитывалась исходя из представлений о точках Лагранжа.Точки Лагранжа-это точки в системе из двух массивных тел, в которых третье тело с пренебрежимо малой массой, на которое не действуют никакие другие силы, кроме гравитационных сил со стороны двух первых тел, может оставаться неподвижным относительно этих тел. | ||
В связи с тем, что для того, чтобы построить эквипотенциальную поверхность с нулевым потенциалом вокруг Земли(а это и есть сфера Хилла), необходимо опираться на сложный математический аппарат, были использованы уже вычисленные значения для геометрического места точек Лагранжа. 1 и 2 точки лежат на прямой,соединяющей центры Земли и Солнца по разную сторону от Земли. Поэтому расстояние от 1 до 2 точки Лагранжа можно считать диаметром сферы Хилла. | В связи с тем, что для того, чтобы построить эквипотенциальную поверхность с нулевым потенциалом вокруг Земли(а это и есть сфера Хилла), необходимо опираться на сложный математический аппарат, были использованы уже вычисленные значения для геометрического места точек Лагранжа. 1 и 2 точки лежат на прямой,соединяющей центры Земли и Солнца по разную сторону от Земли. Поэтому расстояние от 1 до 2 точки Лагранжа можно считать диаметром сферы Хилла. | ||
| − | В случае для Земли масса Земли много меньше массы Солнца, поэтому 1 и 2 точка лежат на примерно одинаковом расстоянии от Земли, и можно считать, что <math>r \approx R \sqrt[3]{\frac{ | + | В случае для Земли масса Земли много меньше массы Солнца, поэтому 1 и 2 точка лежат на примерно одинаковом расстоянии от Земли, и можно считать, что <math>r \approx R \sqrt[3]{\frac{M_{earth}}{3 M_{sun}}}</math> |
== Обсуждение результатов и выводы == | == Обсуждение результатов и выводы == | ||
| + | В результате были получены радиусы всех гравитационных сфер Земли. При подстановке значений в формулы получили значения радиусов, соответствующие общеизвестным и вычисленным ранее значениям. | ||
| + | Соотнести теоретические данные с данными, полученными в ходе моделирования, пока не удаётся: попытки привести значения переменных при моделировании к значению констант системы Земля-Луна-Солнце оказались не плодотворными. Подробнее о результатах моделирования: | ||
| + | *[[КП: Моделирование образования Земли и Луны в газопылевом облаке с учётом солнечного притяжения(моделирование эллипсоида)]] | ||
| + | *[[КП: Динамика молекулы (моделирование)]] | ||
== Ссылки по теме == | == Ссылки по теме == | ||
Текущая версия на 14:36, 28 мая 2013
А.М. Кривцов > Теоретическая механика > Курсовые проекты 2013 > Моделирование образования Земли и Луны в газопылевом облаке с учётом солнечного притяжения (расчет)
Курсовой проект по Теоретической механике
Исполнитель: Григорьева Полина
Группа: 07 (20510)
Семестр: весна 2013
Содержание
Аннотация проекта[править]
Данный проект является продолжением работы над проектом "Земля-Луна", начатый А.М.Кривцовым и А.А.Ле-Захаровым. Исследуется поведение газопылевого облака в гравитационном поле, создаваемом Солнцем.
Постановка задачи[править]
Главная задача - выполнить предварительные расчёты и теоретически предсказать результаты моделирования. Ранее были получены результаты для облака, имеющего форму эллипсоида. Для этого случая были проведены исследования, которые выявили наиболее оптимальные начальные данные, при которых образование двойной системы происходит с большой вероятностью, однако не было теоретически предсказано, на каком расстоянии от Земли должна образовываться Луна.
Общие сведения по теме[править]
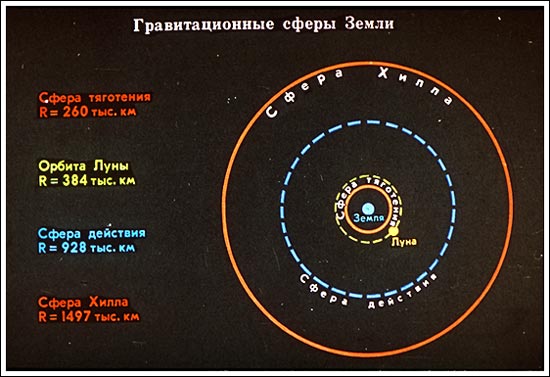
Луна движется не только под влиянием Земли, но и под влиянием Солнца. Однако при этом она остаётся спутником Земли, т.е. находится в области её гравитационного влияния, преобладающего над влиянием Солнца.
В астрономии используется три вида гравитационных сфер: сфера притяжения, сфера действия и сфера Хилла.
Сфера притяжения - такая сфера, в которой гравитационная сила, действующая на спутник со стороны Земли, больше гравитационной силы со стороны Солнца.
Сфера действия - такая сфера, в которой влияние Земли на ускорение спутника значительнее, чем влияние Солнца. Эта сфера не несёт особого физического смысла, однако внутри этой сферы удобнее пользоваться уравнениями в системе отчёта,связанной с Землей, а вне этой сферы - в системе отсчёта, связанной с Солнцем.
Сфера Хилла - область пространства с центром в притягивающей точке - Земле, двигаясь внутри которой тело всегда будет оставаться спутником Земли.[1]
Таким образом, можно сделать вывод: в результате моделирования Луна должна находиться в области пространства, ограниченной сферой притяжения и сферой Хилла.
Действительные радиусы сфер и радиус орбиты Луны:
медиафайл взят с сайта [2]
Решение[править]
Введем общие обозначения: , - расстояние от Земли до Солнца.
- Сфера притяжения
Ищется геометрическое место точек, в которых сила,действующая на спутник в этой точке со стороны Земли больше,чем со стороны Солнца. Фигурой, удовлетворяющей этому условию,является сфера, с центром в точке, отстоящей от точки, в которой располагается Земля, на расстояние (точка лежит на прямой, соединяющей центры Земли и Луны) и радиусом . Для Земли расстояние от центра Земли до центра сферы притяжения на несколько порядков меньше,чем радиус сферы притяжения, поэтому им можно пренебречь и считать центром сферы притяжения центр Земли.
- Сфера действия
Привяжем систему отсчёта к Земле. Тогда ускорение спутника можно разбить на 2 составляющие: в одну в качестве коэффициента входит масса Солнца, в другую - всё остальное. Первую составляющую назовём "возмущающим" ускорением, вторую-"собственным". Отношение этих двух величин обозначим за . Чем меньше значение , тем меньше орбита спутника отличается от Кеплеровской орбиты. Аналогичный коэффициент можем получить,привязав СО к Солнцу. В этом случае "возмущающим" ускорением будет составляющая, в коэффициент при которой входит масса Земли. Область,в которой < , называется сферой действия Земли относительно Солнца. Геометрическим местом всех таких точек является поверхность, задаваемая уравнением в полярных координатах Строго говоря,эта поверхность не является сферой, а представляет собой некий эллипсоид. Однако при малых значениях k поверхность мало отличима от сферы радиусом с центром в точке, совпадающей с центром Земли.
- Сфера Хилла
Сфера Хилла рассчитывалась исходя из представлений о точках Лагранжа.Точки Лагранжа-это точки в системе из двух массивных тел, в которых третье тело с пренебрежимо малой массой, на которое не действуют никакие другие силы, кроме гравитационных сил со стороны двух первых тел, может оставаться неподвижным относительно этих тел. В связи с тем, что для того, чтобы построить эквипотенциальную поверхность с нулевым потенциалом вокруг Земли(а это и есть сфера Хилла), необходимо опираться на сложный математический аппарат, были использованы уже вычисленные значения для геометрического места точек Лагранжа. 1 и 2 точки лежат на прямой,соединяющей центры Земли и Солнца по разную сторону от Земли. Поэтому расстояние от 1 до 2 точки Лагранжа можно считать диаметром сферы Хилла. В случае для Земли масса Земли много меньше массы Солнца, поэтому 1 и 2 точка лежат на примерно одинаковом расстоянии от Земли, и можно считать, что
Обсуждение результатов и выводы[править]
В результате были получены радиусы всех гравитационных сфер Земли. При подстановке значений в формулы получили значения радиусов, соответствующие общеизвестным и вычисленным ранее значениям. Соотнести теоретические данные с данными, полученными в ходе моделирования, пока не удаётся: попытки привести значения переменных при моделировании к значению констант системы Земля-Луна-Солнце оказались не плодотворными. Подробнее о результатах моделирования:
- КП: Моделирование образования Земли и Луны в газопылевом облаке с учётом солнечного притяжения(моделирование эллипсоида)
- КП: Динамика молекулы (моделирование)