КП: Динамика молекулы (моделирование)
Курсовой проект по Теоретической механике
Исполнитель: Марков Николай
Группа: 07 (20510)
Семестр: весна 2013
Содержание
Аннотация проекта
Данный проект является продолжением работы над проектом "Земля-Луна".Исследуется поведение газопылевого облака в гравитационном поле, создаваемом Солнцем. Уже получены результаты для облака, имеющего форму эллипсоида. Результатом является образование двойной системы путём одновременного возникновения двух небесных тел, одно из которых в несколько раз больше другого по размеру. Для этого случая были проведены исследования, которые выявили наиболее оптимальные исходные данные, при которых образование двойной системы происходит с большой вероятностью.
Постановка задачи
Выполнить моделирование динамики газопылевого облака, заданного виде тора в гравитационном поле центрального тела, с получением двойной системы, которая по своим характеристикам была приближена к системе Земля-Луна, а так же получить значения начальных параметров, при котором возникновение такой системы было бы наиболее вероятным.
Общие сведения по теме
Для рассматриваемого случая необходимо учитывать многое из того, что не учитывается в случае, когда облако задается в виде эллипсоида. Скорость твердотельного вращения должна считаться исходя из факта влияния на облако как самих частиц,его составляющих, так и центрального тела. Таким образом, задав скорость вращения облака, можно добиться того, что частицы пыли не будут падать в центр или разлетаться.
Облако в виде тора в поле центрального тела.
Также необходимо учитывать тот факт, что из-за более сложной геометрии тора по сравнению с геометрией эллипсоида, понять где и как будут образовываться необходимые кластеры гораздо сложнее. В случае с эллипсоидом, можно было предполагать образование системы в центральной части, тогда как для тора оно может произойти где угодно. Причем в данном случае может получиться так, что образуется несколько кластеров, подобных друг другу. Таким образом, для вероятности образования двойной системы, необходимо увеличивать толщину тора.
Решение
Для решения данной задачи было проведено ознакомление и изучение результатов, полученных без учета центрального тела для эллипсоида,а так же разбор работы программы, производящей моделирование. Создана модель газопылевого облака в виде тора, а так же исследовано влияние начальной скорости вращения на устойчивость геометрии тора. Рассмотрим решение подробнее:
Пусть имеется частица, имеющая массу , скорость и находящаяся на расстоянии от центрального тела массы . Тогда уравнение будет иметь вид:
.
Если учитывать, что угловая скорость твердотельного вращения без центрального тела имеет вид
, где - число частиц
то получим, что искомая уловая скорость твердотельного вращения будет иметь вид
Задав отношение , получаем значение угловой скорости облака Это отношение угловых скоростей позволяет сохронить подобие при изменении числа частиц.
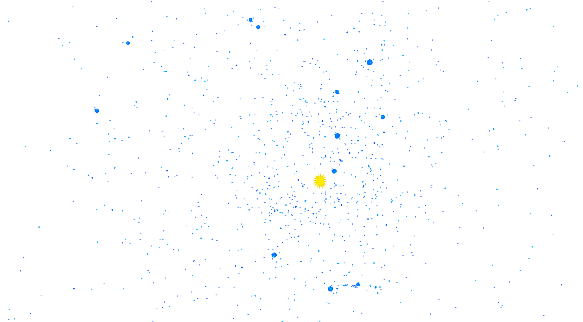
Зная можно найти скорость частицы ,где - расстояние до центра. Результат работы программы при: = 1.05
= 10000
Видим 12 кластеров, движущиеся по орбитам. Этот результат получен после 24804 итераций. То есть при данном отношении угловых скоростей облако устойчиво.
Обсуждение результатов и выводы
Полученные результаты позволяют исследовать зависимость поведения облака от параметров. Попытки привести значения переменных к значению констант системы Земля-Луна-Солнца оказались не плодотворными. Таким образом, для дальнейшего продвижения, необходимо далее исследовать влияние параметром на образование двойной системы. Помимо параметров динамических, необходимо рассматривать влияние и параметров геометрических, после чего уже можно будет пытаться применить к модели реальные параметры