Информатика: Движение тела в среде — различия между версиями
| Строка 133: | Строка 133: | ||
</div> | </div> | ||
| + | <div> | ||
| + | |||
| + | '''[[Бальцер Анастасия]]''' | ||
| + | |||
| + | '''Описание программы''' : программа записывает в четыре файла результаты вычисления: | ||
| + | |||
| + | Координаты, рассчитанные по формуле, при движении без сопротивления воздуха; | ||
| + | Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости; | ||
| + | Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости; | ||
| + | Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости. | ||
| + | |||
| + | Посмотреть программу можно [http://tm.spbstu.ru/File:falling.zip здесь] | ||
| + | |||
| + | </div> | ||
<div class="mw-collapsible mw-collapsed" style="width:100%" > | <div class="mw-collapsible mw-collapsed" style="width:100%" > | ||
| Строка 286: | Строка 300: | ||
</div> | </div> | ||
| + | <div class="mw-collapsible mw-collapsed" style="width:100%" > | ||
| + | '''[[Васильева Анастасия]]''' | ||
| − | + | '''Описание программы''': пользователь вводит начальную скорость полета, угол падения и шаг, с которым будут рассчитаны точки. | |
| − | ''' | ||
| − | + | Программа записывает в один файл результаты вычисления: | |
# Координаты, рассчитанные по формуле, при движении без сопротивления воздуха; | # Координаты, рассчитанные по формуле, при движении без сопротивления воздуха; | ||
| − | # Координаты, полученные методом Верле при | + | # Координаты, полученные при численном интегрировании - метод Эйлера; |
| + | # Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости. | ||
# Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости; | # Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости; | ||
| − | |||
| − | Скачать можно [http://tm.spbstu.ru/Файл: | + | Скачать можно [http://tm.spbstu.ru/Файл:fly.zip тут]. |
| + | |||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| − | |||
| − | |||
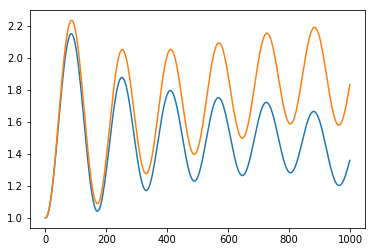
'''Визуализированный результат работы программы''' | '''Визуализированный результат работы программы''' | ||
| − | [[File: | + | [[File:graphick.png]] |
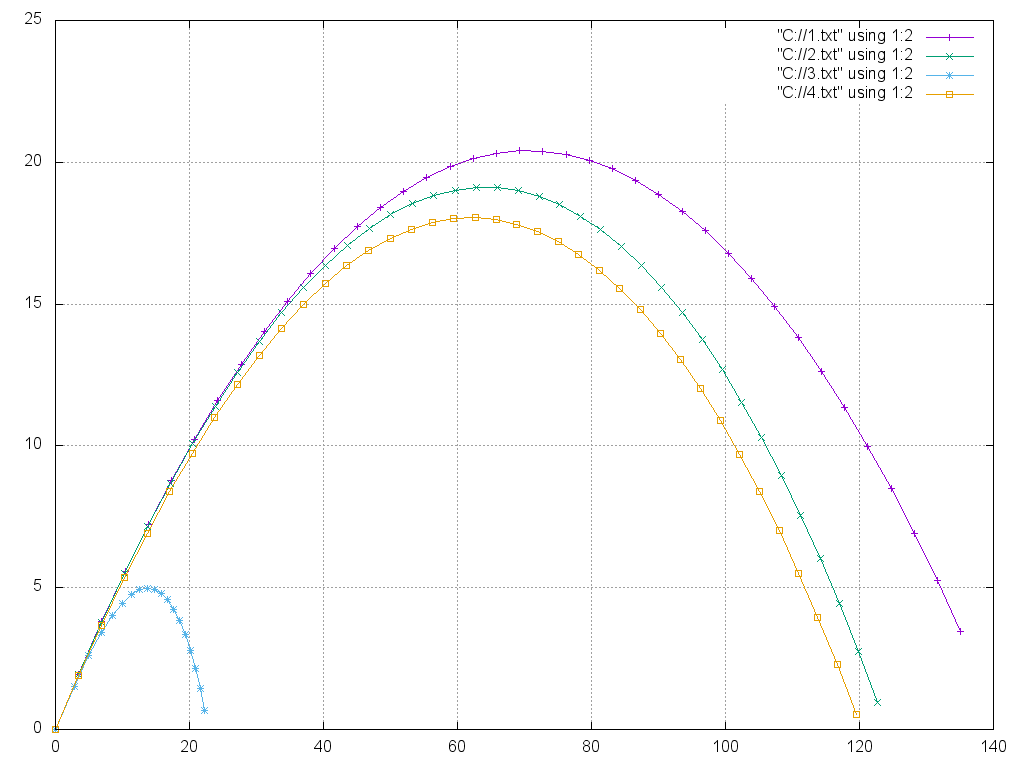
| − | + | Для тела с массой 0.5 кг,сопротивлением воздуха 0.1, угол бросания 30°, начальная скорость 30 м/с, ускорение свободного падения 9.8 м/c^2, шаг 0.001; | |
| − | |||
| − | |||
| − | |||
| + | # "output.txt" using 1 : 2 - координаты, рассчитанные по формуле, при движении без сопротивления воздуха; | ||
| + | # "output.txt" using 3 : 4 - координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости (численное интегрирование - метод Эйлера); | ||
| + | # "output.txt" using 5 : 6 - координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости; | ||
| + | # "output.txt" using 7 : 8 - координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости. | ||
| − | |||
| − | + | <syntaxhighlight lang="cpp" line start="1" enclose="div"> | |
| − | |||
| − | |||
#include <iostream> | #include <iostream> | ||
| + | #include <fstream> | ||
| + | #include <iomanip> | ||
| + | #include <time.h> | ||
| + | #include <conio.h> | ||
| + | #include <stdlib.h> | ||
#include <math.h> | #include <math.h> | ||
| − | |||
#include <cstring> | #include <cstring> | ||
| − | |||
| − | |||
| − | |||
| − | |||
using namespace std; | using namespace std; | ||
| − | + | class pad ///создаем класс | |
| − | |||
| − | |||
| − | class | ||
{ | { | ||
| − | + | private: ///в закрытом доступе | |
| − | + | double *X, *Y, *E, *G, *Z, *S, *V, *U; ///координаты по х и у; *E, *G : численное интегрирование метод Эйлера, *Z, *S- метод верле, *V, *U- точный метод | |
| − | + | double a, g , pi;///ускорение, коэфф свободного падения, значение числа пи | |
| − | + | int Size; ///размер массива- сколько точек считать в первом способе | |
| + | double v, shag, b, vx, vy;///скорость, шаг по времени, угол в градусах скорость по х, скорость по у | ||
| − | + | void SetX() ///создаем функцию для вычисления значенй по х для простого падения и по эйлеру | |
| − | + | { | |
| + | g = 9.8;///коэфф свободного падения | ||
| + | float t = 0; ///время | ||
| + | X = new double [Size];///создаем массив для координат по х для простого падения | ||
| + | E = new double [Size];///создаем массив для координат по х для интегрирования по эйлеру | ||
| + | X[0] = 0; ///задаем значение по х в нуле | ||
| + | E[0] = 0 ; ///задаем значение по х в нуле по эйлеру | ||
| + | for (int i = 1; i < Size; i++) ///задаем цикл от 1 (для нуля мы задали), чтобы считать координаты | ||
{ | { | ||
| − | + | t += shag; ///каждый раз прибавляем по времени шаг | |
| − | + | X[i] = v * cos(a) * t; ///координаты по х для простого падения | |
| − | v | + | E[i] = E[i-1] + v * cos(a) * shag; ///х из интегрирования по эйлеру |
| − | |||
} | } | ||
| + | } | ||
| − | + | void SetY()///создаем функцию для вычисления значенй по у для простого падения и по эйлеру | |
| − | + | { | |
| + | g = 9.8; ///коэфф свободного падения | ||
| + | double Vy; /// переменная для значение скорости по у для метода эйлера | ||
| + | float t = 0; ///время | ||
| + | Y = new double [Size];///создаем массив для координат по у для простого падения | ||
| + | G = new double [Size];///создаем массив для координат по х для интегрирования по эйлеру | ||
| + | Vy = v * sin (a);/// значение скорости по у для метода эйлера | ||
| + | Y[0] = 0;///задаем значение по у в нуле | ||
| + | G[0] = 0;///задаем значение по у в нуле по эйлеру | ||
| + | for (int i = 1; i < Size; i++)///задаем цикл от 1 (для нуля мы задали), чтобы считать координаты | ||
{ | { | ||
| − | + | t += shag; ///каждый раз прибавляем по времени шаг | |
| − | + | Y[i] = v * sin (a) *t - (g * t * t) * 0.5; ///координаты по у для простого падения | |
| − | + | Vy -= g * shag; ///значение скорости по у для метода эйлера | |
| − | + | G[i] = G[i-1] + Vy * shag;///у из интегрирования по эйлеру | |
| − | |||
| − | |||
} | } | ||
| + | } | ||
| − | // | + | void SetVerle() ///функция для метода верле |
| − | + | { | |
| + | double k = 0.1, m = 0.5; ///коэфф сопротивления водуха, масса тела | ||
| + | g = 9.8; /// коэфф свободного падения | ||
| + | uint32_t Size1 = 1000000.0; ///размер массива | ||
| + | S = new double [Size1]; ///создаем массив для значений по х для метода верле | ||
| + | Z = new double [Size1]; ///создаем массив для значений по у для метода верле | ||
| + | vx = v * cos(a); ///формулы для вычисления скорости по оси х | ||
| + | vy = v * sin(a); ///формулы для вычисления скорости по оси у | ||
| + | S[1] = 0; ///значение х метод верле | ||
| + | S[0] = -vx * shag; ///значение в нуле | ||
| + | Z[1] = 0; ///значение у метод верле | ||
| + | Z[0] = -vy * shag; ///значение в нуле | ||
| + | for (int i = 0; i < Size1-2; i++) ///задаем цикл | ||
{ | { | ||
| − | + | S[i+2] = 2.0 * S[i+1] - S[i] - (k / m) * v * vx * shag * shag;///значения по х для верле | |
| − | + | vx = 0.5 * ( 1.0 / shag )* ( S[i+2] - S[i]);///считаем значения скорости по оси х | |
| + | Z[i+2] = 2.0 * Z[i+1] - Z[i] - ( g + (k / m) * v * vy ) * shag * shag;///значения по х для верле | ||
| + | vy = 0.5 * ( 1.0 / shag )* ( Z[i+2] - Z[i]);///считаем значения скорости по оси х | ||
| + | v = sqrt (vx * vx + vy * vy); ///модуль общей скорости | ||
} | } | ||
| − | + | } | |
| − | + | void SetVerleLast() ///функция для точного метода верле | |
| − | + | { | |
| − | + | double k = 0.1, m = 0.5;///коэфф сопротивления водуха, масса тела | |
| − | + | g = 9.8; /// коэфф свободного падения | |
| − | + | uint32_t Size2 = 1000000.0; ///размер массива | |
| − | + | float t = 0; ///время | |
| − | // | + | V = new double [Size2]; ///создаем массив для значений по х для точного метода верле |
| − | + | U = new double [Size2]; ///создаем массив для значений по у для точного метода верле | |
| + | vx = v * cos(a); ///формулы для вычисления скорости по оси х | ||
| + | vy = v * sin(a); ///формулы для вычисления скорости по оси у | ||
| + | ///double e = 2.7 ;///значение экспоненты | ||
| + | V[0] = 0; ///значение х точный метод верле | ||
| + | U[0] = 0; ///значение у точный метод верле | ||
| + | for (int i = 1; i < Size2; i++) | ||
{ | { | ||
| − | + | t += shag; ///увеличиваем время на шаг | |
| − | + | V[i] = vx * (m / k) * (1.0 - exp(((-k) / m) * t)); ///значения по х для точного верле | |
| − | + | U[i] = (m / k) * (vy + g * (m / k)) * (1.0 - (exp(((-k) / m) * t))) - g * t * (m / k);///значения по х для точного верле | |
} | } | ||
| + | } | ||
| − | // | + | public: ///в открытом |
| − | + | pad() | |
| − | + | { | |
| − | + | X = 0; ///зануляем значения | |
| − | + | Y = 0; | |
| − | + | Size = 0; | |
| − | + | v = 0; | |
| − | + | shag = 0; | |
| − | + | b = 0; | |
| − | } | + | } |
| + | pad(double _v, double _shag, double _b) ///конструктор с параметрами | ||
| + | { | ||
| + | pi = M_PI; ///значение числа пи | ||
| + | g = 9.8; ///коэфф свободного падения | ||
| + | v = _v;/// присваиваем значения переменных значению параметров в конструкторе | ||
| + | shag = _shag; | ||
| + | b = _b; | ||
| + | a = (pi * b) / 180.0 ; ///вычисляем значение угла в радианах | ||
| + | double t = (2.0 * v * sin(a)) / g; /// считаем значение времени | ||
| + | Size = abs( t / shag )+1;///ищем значение размера массива | ||
| + | SetX(); ///вызываем функции зависящие от параметров конструктора | ||
| + | SetY(); | ||
| + | SetVerle(); | ||
| + | SetVerleLast(); | ||
| + | } | ||
| − | + | void FilePrint() ///функция записи в файл | |
| − | + | { | |
| − | + | ofstream fout("output.txt"); ///открываем файл уже созданный в папке с программой | |
| − | + | fout << "X: " << " Y: " << " E: " << " G: " << " S: " << " Z: "<< " V: "<< " U: "<<"\n" ; ///выводим стоку с разными названиями массивов, соотв. координатам по х и у различных методов | |
| − | + | for (int i = 0; i < Size; i++) ///цикл | |
| − | + | fout << X[i] << " " << Y[i] << " " << E[i] << " " << G[i] << " " << S[i] << " " << Z[i] << " " << V[i] <<" "<< U[i] <<"\n"; ///забивает сами значения массивов | |
| − | + | fout.close();///закрываем файл | |
| + | }; | ||
| + | }; | ||
| − | + | int main()/// основная функция | |
| − | + | { | |
| − | + | double shag, b, v; ///шаг, угол в градусах, скорость начальная | |
| − | + | cout << "vvedite v "; ///просим пользователя ввести значение скорости начальной | |
| − | + | cin >> v; ///считываем начальную скорость | |
| + | cout << "vvedite ygol ";///просим пользователя ввести угол в градусах | ||
| + | cin >> b;/// считываем угол | ||
| + | cout << "vvedite shag ";///просим пользователя ввести шаг по времени | ||
| + | cin >> shag; ///считываем значение шага | ||
| + | pad F1(v, shag, b); ///объявление коструктора, создание функции F1 с переменными v, shag, b | ||
| + | F1.FilePrint(); ///вызываем функцию для записи файла | ||
| + | } | ||
| + | </syntaxhighlight> | ||
| + | </div> | ||
| − | + | '''[[Гильманов Илья]]''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Описание программы''': программа состоит из четырех независимых друг от друга частей: | |
| − | + | # Полет тела без сопротивления воздуха; | |
| − | + | # Полет тела при линейной зависимости силы сопротивления воздуха от скорости, при котором координаты тела рассчитываются точным методом; | |
| − | + | # Полет тела при линейной зависимости силы сопротивления воздуха от скорости, при котором координаты тела рассчитываются методом Верле; | |
| − | + | # Полет тела при квадратичной зависимости силы сопротивлении воздуха от скорости, при котором координаты тела рассчитываются методом Верле; | |
| + | |||
| + | Скачать можно [[http://mech.spbstu.ru/File:Движение_тела_в_среде.rar тут]] | ||
| + | |||
| + | <div class="mw-collapsible mw-collapsed" style="width:100%" > | ||
| + | '''[[Демченко Артём]]''' | ||
| − | + | '''Описание программы''': программа записывает в четыре файла результаты вычисления: | |
| − | + | # Координаты, рассчитанные по формуле, при движении без сопротивления воздуха; | |
| − | + | # Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости; | |
| − | + | # Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости; | |
| − | + | # Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости. | |
| − | + | ''' Инструкция ''': | |
| − | + | Пользователь вводит начальные данные ( массу, скорость, угол броска, шаг по времени и сопротивление воздуха). Выбираем режим работы программы, после этого в папке с программой создается файл, который требуется открыть программой gnuplot для просмотра графика, построенного на полученных координатах. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <div class="mw-collapsible-content"> | |
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Визуализированный результат работы программы''' | |
| − | + | [[:File:Throws.png]] | |
| − | |||
| − | |||
| − | + | <syntaxhighlight lang="cpp" line start="1" enclose="div"> | |
| − | + | #include <iostream> | |
| − | + | #include <math.h> | |
| − | + | #include <iomanip> | |
| − | + | #include <fstream> | |
| − | + | #include <conio.h> | |
| − | + | #include <stdio.h> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | using namespace std; | |
| − | |||
| − | |||
| − | |||
| − | + | double g = 9.8, Pi = 3.1415; // Задаем две глобальные переменные ускорения свободного падения и числа Pi | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | int WoutR(double alpha, double dt, double t, double Yo, double Vo) // Функция, записывающая в файл Throws Without Resistance.txt координаты тела, которое движется без сопротивления | |
| − | + | { | |
| − | + | FILE *Coord; | |
| − | + | Coord = fopen ("Throws Without Resistance.txt", "w"); | |
| + | double X = 0, Y = 0; // Координаты начала | ||
| − | + | while ( Y >= Yo) // Yo используем для того, чтобы цикл прекратился тогда, когда тело упадет | |
| − | + | { | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | X = Vo*t*cos(alpha); | ||
| + | Y = Vo*t*sin(alpha) - (g*t*t)*0.5; | ||
| + | t+= dt; | ||
| + | if (Y > Yo ) | ||
| + | fprintf(Coord, "%.3lf \t %.3lf\n", X, Y); | ||
| + | else | ||
| + | fprintf(Coord, "%.3lf \t %.3lf\n", X, 0.000); // Используем такой else для того, чтобы не получить отрицательную координату | ||
| + | } | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
} | } | ||
| − | |||
| − | + | int ExactForm(double alpha, double dt, double t, double Yo, double Vo, double R, double m) // Функция, записывающая в файл ExactForm.txt координаты тела, рассчитывающиеся по формлуе точного решения | |
| − | + | { // для линейной зависимости | |
| − | + | FILE *Coord; | |
| − | + | Coord = fopen ("ExactForm.txt", "w"); | |
| + | double X, Y = 0, Vx, Vy; | ||
| − | + | while ( Y >= Yo) // Использование Yo аналогично использованию в прошлом пункте. | |
| − | { | + | { |
| − | |||
| − | |||
| − | + | X = ((m*Vx)/R) * (1 - exp(((-1)*R*t)/m)); | |
| − | + | Y = (m/R)*((Vy + (g*m)/R)*(1 - exp((-1)*R*t/m))) - (g*t*m)/R; | |
| − | + | Vx = Vo*cos(alpha); | |
| − | + | Vy = Vo*sin(alpha); | |
| − | + | t+= dt; | |
| − | + | if (Y > Yo ) | |
| − | + | fprintf(Coord, "%.3lf \t %.3lf\n", X, Y); | |
| − | + | else | |
| − | + | fprintf(Coord, "%.3lf \t %.3lf\n", X, 0.000); // используется аналогично прошлому пункту | |
| + | } | ||
} | } | ||
| − | double | + | int VerleSq (double alpha, double dt, double t, double Yo, double Xo, double Vo, double R, double m) // Функция, записывающая в файл VerleSq.txt оординаты тела, рассчитывающиеся по формлуе Верле |
| − | { | + | { // для Квадратичной зависимости сопротивления от скорости |
| − | + | FILE *Coord; | |
| − | + | Coord = fopen ("VerleSq.txt", "w"); | |
| − | + | double X, Xnext, Xprev, Y, Ynext, Yprev, Vx, Vy, V, Yop, Xop; // X, Y - текущие координаты; Xnext, Ynext - координаты следующего шага; Xprev, Yprev - координаты предыдущего шага. | |
| − | + | // Xop, Yop - вспомогательные координаты для (-1)-го шага | |
| − | + | ||
| − | + | Yop = Yo - Vo*sin(alpha)*dt; // Сторки 62-79 используются для просчитывания (-1)-го шага, так как в точке 0;0 у нас нету предыдущего шага | |
| − | + | Xop = Xo - Vo*cos(alpha)*dt; | |
| + | X = Xo; | ||
| + | Y = Yo; | ||
| + | Xnext = 2.0*X - Xop - (R/m)*Vo*Vo*cos(alpha)*(dt*dt); | ||
| + | Vx = (1.0/(2.0*dt))*(Xnext - Xop); | ||
| + | Ynext = 2.0*Y - Yop - (g +(R/m)*Vo*Vo*sin((alpha)))*(dt*dt); | ||
| + | Vy = (1.0/(2.0*dt))*(Ynext - Yop); | ||
| + | V = sqrt((Vo*cos(alpha)*Vo*cos(alpha)) + (Vo*sin(alpha)*Vo*sin(alpha))); | ||
| − | + | fprintf(Coord, "%.3lf \t %.3lf\n", X, Y); // Записываем первую координату в файл | |
| − | |||
| − | |||
| − | |||
| − | + | Xprev = X; // Меняем координаты местами. Так (n-1)-ый шаг становится n-ым шагом, n-ый шаг становится (n+1)-ым шагом. Далее аналогично | |
| − | + | X = Xnext; | |
| − | + | Yprev = Y; | |
| − | + | Y = Ynext; | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | while (Y >= Yo) // После выполнения строк 62-79 получаем все необходимые данные для выполнения алгоритма. | |
| − | { | + | { |
| − | + | Xnext = 2.0*X - Xprev - (R/m)*V*Vx*(dt*dt); | |
| − | + | Vx = (1.0/(2.0*dt))*(Xnext - Xprev); | |
| − | + | Ynext = 2.0*Y - Yprev - (g +(R/m)*V*Vy)*(dt*dt); | |
| + | Vy = (1.0/(2.0*dt))*(Ynext - Yprev); | ||
| + | V = sqrt((Vx*cos(alpha)*Vx*cos(alpha)) + (Vy*sin(alpha) - g*dt)*(Vy*sin(alpha) - g*dt)); | ||
| + | if (Ynext > Yo ) | ||
| + | fprintf(Coord, "%.3lf \t %.3lf\n", Xnext, Ynext); | ||
| + | else | ||
| + | |||
| + | fprintf(Coord, "%.3lf \t %.3lf\n", X, 0.000); | ||
| − | + | Xprev = X; | |
| − | + | X = Xnext; | |
| − | + | Yprev = Y; | |
| − | + | Y = Ynext; | |
| − | } | + | } |
| − | |||
| − | |||
| − | |||
} | } | ||
| − | + | int VerleL (double alpha, double dt, double t, double Yo, double Xo, double Vo, double R, double m) // Функция, записывающая в файл VerleL.txt оординаты тела, рассчитывающиеся по формлуе Верле | |
| − | + | { // для линейной зависимости сопротивления от скорости | |
| − | + | FILE *Coord; | |
| + | Coord = fopen ("VerleL.txt", "w"); | ||
| + | double X, Xnext, Xprev, Y, Ynext, Yprev, Vx, Vy, V,Yop, Xop; // Комментарии аналогичны переменным и формулам в VtrleSq | ||
| + | Yop = Yo - Vo*sin(alpha)*dt; | ||
| + | Xop = Xo - Vo*cos(alpha)*dt; | ||
| + | X = Xo; | ||
| + | Y = Yo; | ||
| + | Xnext = 2.0*X - Xop - (R/m)*Vo*Vo*cos(alpha)*(dt*dt); | ||
| + | Vx = (1.0/(2.0*dt))*(Xnext - Xop); | ||
| + | Ynext = 2.0*Y - Yop - (g +(R/m)*Vo*Vo*sin((alpha)))*(dt*dt); | ||
| + | Vy = (1.0/(2.0*dt))*(Ynext - Yop); | ||
| + | V = sqrt((Vo*cos(alpha)*Vo*cos(alpha)) + (Vo*sin(alpha)*Vo*sin(alpha))); | ||
| − | + | fprintf(Coord, "%.3lf \t %.3lf\n", X, Y); | |
| − | |||
| − | + | Xprev = X; | |
| − | + | X = Xnext; | |
| − | + | Yprev = Y; | |
| − | + | Y = Ynext; | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | while (Y >= Yo) | ||
| + | { | ||
| + | Xnext = 2.0*X - Xprev - (R/m)*Vx*(dt*dt); | ||
| + | Vx = (1.0/(2.0*dt))*(Xnext - Xprev); | ||
| + | Ynext = 2.0*Y - Yprev - (g +(R/m)*Vy)*(dt*dt); | ||
| + | Vy = (1.0/(2.0*dt))*(Ynext - Yprev); | ||
| + | if (Ynext > Yo ) | ||
| + | fprintf(Coord, "%.3lf \t %.3lf\n", Xnext, Ynext); | ||
| + | else | ||
| + | fprintf(Coord, "%.3lf \t %.3lf\n", Xnext, 0.000); | ||
| − | + | Xprev = X; | |
| + | X = Xnext; | ||
| + | Yprev = Y; | ||
| + | Y = Ynext; | ||
| + | } | ||
| + | } | ||
| − | + | int main() | |
| − | + | { | |
| + | double alpha, Vo, dt, R, m , t = 0, Yo = 0, Xo = 0; // Объявляем переменные: alpha - угол броска; Vo - начальная скорость; dt - шаг по времени; R- коэф. сопротивления; m- масса тела; | ||
| + | // t = 0 - начало отсчета времени с 0; Yo = 0, Xo = 0 - координаты начала | ||
| + | int i = 0; // переменная для оператора switch | ||
| − | + | cout << "Enter start speed:\n"; | |
| + | cin >> Vo; // Вводим с клавиатуры начальную скорость | ||
| + | cout << "Enter angle in grades ( from 0 to 180 ):\n"; | ||
| + | cin >> alpha; // Вводим с клавиатуры угол броска в градусах | ||
| + | alpha = alpha*Pi / 180; // переводим угол броска из градусов в радианы | ||
| + | cout << "Enter mass:\n"; | ||
| + | cin >> m; // Вводим с клавиатуры массу | ||
| + | cout << "Enter precision:\n"; | ||
| + | cin >> dt; // Вводим с клавиатуры шаг по времени | ||
| + | cout << "Enter resistance:\n"; | ||
| + | cin >> R; // Вводим сопротивление воздуха | ||
| + | cout << "Press 1 to draw graph without resistance\n\n" | ||
| + | "Press 2 to draw graph in Exact form\n\n" | ||
| + | "Press 3 to draw graph in VerleSq form\n\n" | ||
| + | "Press 4 to draw graph in VerleL form\n\n" | ||
| + | "Press 5 to draw all graphs at the same time\n\n" | ||
| + | "Press 0 to quit\n\n"; | ||
| + | cin >> i; | ||
| + | cout << "\nPress any button\n"; | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | FILE *Gnu; | ||
| + | Gnu = fopen ("Throws.gp", "w"); // Создаем файл формата gp, который будем открывать программой gnuplot для того, чтобы построить наш график/ки по точкам | ||
| + | |||
| + | switch ( i ) | ||
| + | { | ||
| + | case 1: | ||
| + | { | ||
| + | WoutR(alpha,dt,t,Yo,Vo); | ||
| + | fprintf(Gnu, "plot \"Throws Without Resistance.txt\" using 1:2 w l"); | ||
| + | break; | ||
| + | } | ||
| + | case 2: | ||
| + | { | ||
| + | ExactForm(alpha,dt,t,Yo,Vo,R,m); | ||
| + | fprintf(Gnu, "plot \"ExactForm.txt\" using 1:2 w l"); | ||
| + | break; | ||
| + | } | ||
| + | case 3: | ||
| + | { | ||
| + | VerleSq(alpha,dt,t,Yo,Xo,Vo,R, m); | ||
| + | fprintf(Gnu, "plot \"VerleSq.txt\" using 1:2 w l"); | ||
| + | break; | ||
| + | } | ||
| + | case 4: | ||
| + | { | ||
| + | VerleL(alpha,dt,t,Yo,Xo,Vo,R, m); | ||
| + | fprintf(Gnu, "plot \"VerleL.txt\" using 1:2 w l"); | ||
| + | break; | ||
| + | } | ||
| + | case 5: | ||
| + | { | ||
| + | WoutR(alpha,dt,t,Yo,Vo); | ||
| + | ExactForm(alpha,dt,t,Yo,Vo,R,m); | ||
| + | VerleSq(alpha,dt,t,Yo,Xo,Vo,R, m); | ||
| + | VerleL(alpha,dt,t,Yo,Xo,Vo,R, m); | ||
| + | fprintf(Gnu, "plot \"Throws Without Resistance.txt\" using 1:2 w l, \"ExactForm.txt\" using 1:2 w l, \"VerleSq.txt\" using 1:2 w l, \"VerleL.txt\" using 1:2 w l"); // записываем в Throws.gp названия четырех файлов | ||
| + | break; | ||
| + | } // с координатами таким образом, чтобы программа gnuplot смогла их увидеть и прочесть | ||
| + | case 0: | ||
| + | break; | ||
| + | default: | ||
| + | break; | ||
| + | } | ||
| + | return 0; | ||
| + | } | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | </div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''[[Иванова Яна]]''' | |
| − | + | ||
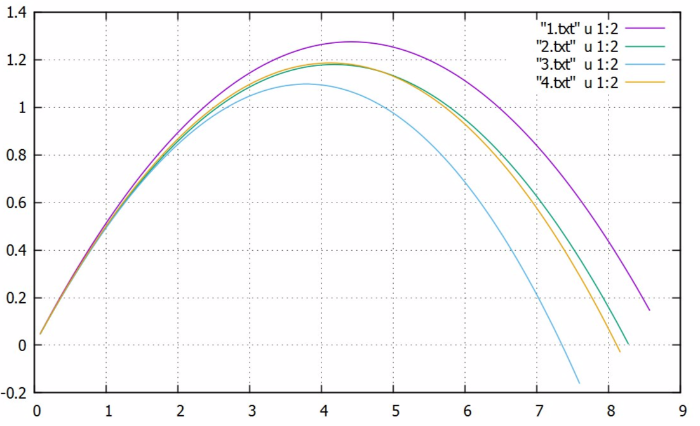
| − | + | '''Описание программы''': в программе выполняются четыре метода подсчета координат тела, брошенного под углом к горизонту. Координаты записываются в файл, строятся четыре графика, иллюстрирующие поведение тела при полете. Код написан для определенных начальных условий (для примера), если Вы хотите выполнить расчет для другой конфигурации, внесите изменения в начальные данные программы в самом коде. | |
| − | + | Начальная скорость: 40 м/с, угол бросания: 45 градусов, коэффициент сопротивления воздуха: 0.023, шаг по времени : 0.1 секунды. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Скачать программу можно [http://tm.spbstu.ru/File:main.zip здесь] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <div class="mw-collapsible-content"> | |
| − | + | '''Визуализированный результат работы программы'''[[File:graph.png]] | |
| − | + | ||
| − | + | [[:File:graph.png]] | |
| − | + | ||
| − | + | <syntaxhighlight lang="cpp" line start="1" enclose="div"> | |
| − | + | #include <iostream> | |
| − | + | #include <math.h> | |
| − | + | #include <iomanip> | |
| − | + | #include <fstream> | |
| − | + | #include <conio.h> | |
| − | + | ||
| − | + | ||
| − | + | using namespace std; | |
| − | + | ||
| − | + | ofstream outfile; | |
| − | + | ||
| − | + | double perevod (double angle) //перевод из градусов в радианы | |
| − | + | { | |
| − | + | return (angle * M_PI / 180 ); | |
| − | + | } | |
| − | + | ||
| − | + | ||
| + | int main() | ||
| + | { | ||
| + | //объявление переменных и задание начальных значений | ||
| + | double X, Xnext, Xprev, Y, Ynext, Yprev, Vx, Vy, V, | ||
| + | m = 1 , dt = 0.1 , g = 9.8,t = 0, | ||
| + | ugol = 45, alpha, R = 0.023, Xo = 0, Yo = 0, Vo = 40; | ||
| + | |||
| + | alpha = perevod (ugol); | ||
| + | |||
| + | //точное решение для случая движения без сопротивления воздуха | ||
| + | Y = Yo; | ||
| + | X = Xo; | ||
| + | |||
| + | outfile.open("1.txt"); | ||
| + | |||
| + | while (Y >= Yo) | ||
{ | { | ||
| − | + | X = Xo + Vo * cos(alpha) * t; | |
| − | + | Vx = Vo * cos(alpha); | |
| − | + | Y = Yo + Vo * sin(alpha) * t - 0.5 * g * t * t; | |
| − | + | Vy = Vo * sin(alpha) - g * t; | |
| − | + | t += dt; | |
| − | + | ||
| − | + | outfile << X << ' ' << Y << endl; | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
} | } | ||
| + | outfile.close(); | ||
| + | |||
| + | //начальные условия для квадратичной зависимости (метод Верле) | ||
| + | Yprev = Yo - Vo*sin(alpha)*dt; | ||
| + | Xprev = Xo - Vo*cos(alpha)*dt; | ||
| + | X = Xo; | ||
| + | Y = Yo; | ||
| + | V = Vo; | ||
| + | Vx = Vo * cos(alpha); | ||
| + | Vy = Vo * sin(alpha); | ||
| − | + | outfile.open("2.txt"); | |
| − | + | ||
| + | while (Y >= Yo) | ||
{ | { | ||
| − | + | Xnext = 2.0 * X - Xprev - (R / m) * V * Vx * (dt * dt); | |
| − | + | Vx = ( Xnext - Xprev )/ (2.0 * dt); | |
| − | + | Ynext = 2.0 * Y - Yprev - (g + (R / m) * V * Vy) * (dt * dt); | |
| − | + | Vy = (Ynext - Yprev)/ (2.0 * dt); | |
| − | + | V = sqrt(Vy*Vy + Vx*Vx ); | |
| − | + | outfile << X << ' ' << Y << endl; | |
| − | + | ||
| − | + | Xprev = X; | |
| − | + | X = Xnext; | |
| − | + | Yprev = Y; | |
| − | + | Y = Ynext; | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
} | } | ||
| + | outfile.close(); | ||
| + | |||
| + | //начальные условия для линейной зависимости (метод Верле) | ||
| + | Yprev = Yo - Vo*sin(alpha)*dt; | ||
| + | Xprev = Xo - Vo*cos(alpha)*dt; | ||
| + | X = Xo; | ||
| + | Y = Yo; | ||
| + | V = Vo; | ||
| + | Vx = Vo * cos(alpha); | ||
| + | Vy = Vo * sin(alpha); | ||
| + | |||
| + | outfile.open("3.txt"); | ||
| − | + | while (Y >= Yo) | |
{ | { | ||
| − | + | Xnext = 2.0 * X - Xprev - (R / m) * Vx * (dt * dt); | |
| − | + | Vx = ( Xnext - Xprev )/ (2.0 * dt); | |
| − | + | Ynext = 2.0 * Y - Yprev - (g + (R / m) * Vy) * (dt * dt); | |
| − | + | Vy = (Ynext - Yprev)/ (2.0 * dt); | |
| − | + | V = sqrt(Vy*Vy + Vx*Vx ); | |
| − | + | outfile << X << ' ' << Y << endl; | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | < | ||
| + | Xprev = X; | ||
| + | X = Xnext; | ||
| + | Yprev = Y; | ||
| + | Y = Ynext; | ||
| + | } | ||
| + | outfile.close(); | ||
| + | //точное решения для линейной зависимости | ||
| + | Y = Yo; | ||
| + | X = Xo; | ||
| + | t = 0; | ||
| − | + | outfile.open("4.txt"); | |
| − | + | while (Y >= Yo) | |
| − | + | { | |
| + | Vx = Vo * cos(alpha); | ||
| + | Vy = Vo * sin(alpha); | ||
| + | X = (m * Vx / R)* (1 - exp(-1 * R * t / m)); | ||
| + | Y = (m/R)*((Vy + g * m / R)*(1 - exp(-1 * R * t / m)) - g * t); | ||
| + | t += dt; | ||
| + | outfile << X << ' ' << Y << endl; | ||
| + | } | ||
| + | outfile.close(); | ||
| − | + | return 0; | |
| − | + | } | |
| − | |||
| − | + | </syntaxhighlight> | |
| + | </div> | ||
| − | < | + | <div> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''[[Капитанюк Светлана]]''' | ||
| − | + | '''Описание программы''' : программа записывает в четыре файла результаты вычисления: | |
| − | + | Координаты, рассчитанные по формуле, при движении без сопротивления воздуха; | |
| + | Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости; | ||
| + | Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости; | ||
| + | Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости. | ||
| − | + | Скачивать [http://tm.spbstu.ru/File:Point_03.zip тут] | |
| − | |||
| − | |||
| − | |||
| + | </div> | ||
| − | + | <div> | |
| − | + | '''[[Киселёв Лев]]''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Описание программы''': программа рассчитывает координаты точки при следующих случаях | |
| + | # Полет тела без сопротивления воздуха; | ||
| + | # Полет тела при линейной зависимости силы сопротивления воздуха от скорости, при котором координаты тела рассчитываются точным методом; | ||
| + | # Полет тела при линейной зависимости силы сопротивления воздуха от скорости, при котором координаты тела рассчитываются методом Верле; | ||
| + | # Полет тела при квадратичной зависимости силы сопротивлении воздуха от скорости, при котором координаты тела рассчитываются методом Верле; | ||
| − | + | Скачать можно [[http://mech.spbstu.ru/File:3zadanie.rar тут]] | |
| − | + | </div> | |
| − | |||
| − | + | <div class="mw-collapsible mw-collapsed" style="width:100%" > | |
| + | '''[[Лебедев Станислав]]''' | ||
| − | + | '''Описание программы''': программа записывает в четыре файла результаты вычисления: | |
| − | + | # Координаты, рассчитанные по формуле, при движении без сопротивления воздуха; | |
| − | + | # Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости; | |
| − | + | # Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости; | |
| − | + | # Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости. | |
| − | |||
| − | |||
| − | + | Скачать можно [http://tm.spbstu.ru/Файл:Шарик.rar тут]. | |
| − | |||
| − | |||
| − | + | <div class="mw-collapsible-content"> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[File:1.png]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Визуализированный результат работы программы''' | |
| − | + | [[File:graph.png]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | # o1 - координаты, рассчитанные по формуле, при движении без сопротивления воздуха; | |
| − | + | # o2 - координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости; | |
| − | + | # o3 - координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости; | |
| − | + | # o4 - координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Для тела с массой 10,сопротивлением воздуха 1, угол бросания 30°, начальная скорость 30 м/с, ускорение свободного падения 9.8 м/c^2; | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ''Примечание: графики o1 и o2 намеренно посчитаны с малой точностью, чтобы графики не сливались.'' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Файл "'''main.cpp'''" | |
| − | + | <syntaxhighlight lang="cpp" line start="1" enclose="div"> | |
| − | + | #include <iostream> | |
| − | + | #include <math.h> | |
| + | #include "Vector.h" | ||
| + | #include <cstring> | ||
| + | #include <cmath> | ||
| + | #include <malloc.h> | ||
| + | #include <fstream> | ||
| − | + | using namespace std; | |
| − | + | int n = 100; | |
| − | + | ofstream outfile; | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | class Ball //класс бросаемого тела | |
| + | { | ||
| + | private: | ||
| + | double angle,m,k; //угол броска,масса,коэффицент сопротивления воздуха | ||
| + | Vector3D r,v,a; //радиус-вектор,вектор скорости,ускорения | ||
| + | public: | ||
| − | } | + | //задание начальных параметров через угол,начальное положение,скорость и ускорение,с которым движется тело. Без сопротивления воздуха |
| + | Ball(double _angle, Vector3D _r, Vector3D _v, Vector3D _a) | ||
| + | { | ||
| + | angle = _angle; | ||
| + | r = _r; | ||
| + | v = _v; | ||
| + | a = _a; | ||
| + | } | ||
| − | + | //задание начальных параметров через угол,начальное положение,скорость и ускорение,с которым движется тело. Без сопротивления воздуха | |
| − | + | Ball(double _angle, double _m, double _k, Vector3D _r, Vector3D _v, Vector3D _a) | |
| + | { | ||
| + | angle = _angle; | ||
| + | r = _r; | ||
| + | v = _v; | ||
| + | a = _a; | ||
| + | m = _m; | ||
| + | k = _k; | ||
| + | } | ||
| + | //точная формула зависимости координаты от времени | ||
| + | Vector3D positionReal(double t) | ||
| + | { | ||
| + | double c1 = m/k,c2 = fabs(a.y)*c1, c3 = exp(-t/c1), c4 = c2*t; | ||
| + | return MakeVector(v.x*c1*(1 - c3), c1*(v.y + c2)*(1 - c3) - c4 , 0 ); | ||
| + | } | ||
| − | < | + | //вывод положения на экран |
| − | + | void writePosToScreen() | |
| + | { | ||
| + | cout << r.x << " " << r.y << " " << r.z << endl; | ||
| + | } | ||
| − | + | //вывод положения в файл | |
| − | + | void writePosToFile(char s[]) | |
| − | + | { | |
| − | + | outfile.open(s,ios :: app); | |
| − | + | outfile << r.x << " " << r.y << endl; | |
| + | outfile.close(); | ||
| + | } | ||
| − | < | + | //вывод произвольного вектора на экран |
| + | void WVTS(Vector3D v) | ||
| + | { | ||
| + | cout.width(15); | ||
| + | cout << v.x; | ||
| + | cout.width(15); | ||
| + | cout << v.y; | ||
| + | cout.width(15); | ||
| + | cout << v.z << endl; | ||
| + | } | ||
| − | [ | + | //вывод произвольного вектора в файл |
| + | void WVTF(Vector3D v,char s[]) | ||
| + | { | ||
| + | outfile.open(s,ios :: app); | ||
| + | outfile << v.x << " " << v.y << endl; | ||
| + | outfile.close(); | ||
| + | } | ||
| − | + | //"пересчет" координаты по Верле(Линейная зависмость) | |
| − | + | void changeR(Vector3D r1, double dt) | |
| − | + | { | |
| − | + | r = MakeVector(2 * r.x - r1.x - k/m*v.x*dt*dt,2*r.y - r1.y - (abs(a.y) + k/m*v.y)*dt*dt, 0 ); | |
| − | + | } | |
| − | |||
| + | //"пересчет" координаты по Верле(Квадратичная зависимость) | ||
| + | void changeRSQ(Vector3D r1, double dt) | ||
| + | { | ||
| + | r = MakeVector(2 * r.x - r1.x - k/m*Length(v)*v.x*dt*dt,2*r.y - r1.y - (abs(a.y) + k/m*Length(v)*v.y)*dt*dt, 0 ); | ||
| + | } | ||
| + | //пересчет скорости по Верле | ||
| + | void changeV(Vector3D r1,double dt) | ||
| + | { | ||
| + | v =VS((VmV(r,r1)),1/(2*dt)); | ||
| + | } | ||
| − | + | //рассчет предыдущегт к 0ому элементу | |
| − | + | Vector3D MR1(double dt) | |
| + | { | ||
| + | return MakeVector(r.x - v.x * dt,r.y - v.y * dt,0); | ||
| + | } | ||
| − | + | //возращает координату тела | |
| − | + | Vector3D getR() | |
| − | + | { | |
| − | + | return r; | |
| − | + | } | |
| − | + | //рассчет времени полета | |
| + | double TimeOfFly() | ||
| + | { | ||
| + | return (2*Length(v)*sin(angle)/Length(a)); | ||
| + | } | ||
| − | + | //рассчет координаты по точной формуле. без сопротивления воздуха. | |
| + | Vector3D position(double t) | ||
| + | { | ||
| + | return MakeVector(r.x + v.x*t + a.x*t*t/2,r.y + v.y*t + a.y*t*t/2,r.z + v.z*t + a.z*t*t/2); | ||
| + | } | ||
| − | + | }; | |
| − | + | int main() | |
| − | + | { | |
| − | + | //задание начальных параметров | |
| − | + | Vector3D g = {0,-9.8,0}; | |
| − | + | double a,dt = 0; | |
| − | + | char s[20]; | |
| − | + | ||
| − | + | // cin >> dt; | |
| − | double | ||
| − | |||
| − | + | dt = 0.1; | |
| + | a = (M_PI * 30)/180; | ||
| + | Ball b1(a, MakeVector(0,0,0),MakeVector(30,a),g); | ||
| − | + | double tof = b1.TimeOfFly()+1; //единичка прибавлена,чтобы график красивым был | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | //Без сопротивления возлуха | |
| − | + | strcpy(s,""); | |
| − | + | strcat(s, "o1.txt"); | |
| − | + | outfile.open(s, ios :: trunc); | |
| − | + | outfile.close(); | |
| − | + | for (double i = 0; i <= tof; i += dt) | |
| − | + | { | |
| − | + | b1.WVTS(b1.position(i)); | |
| − | + | b1.WVTF(b1.position(i), s); | |
| − | + | } | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | //Верле(Линейная зависимость) | |
| − | + | dt = 0.1; | |
| + | a = (M_PI * 30)/180; | ||
| + | Ball b2(a,10 , 1, MakeVector(0,0,0),MakeVector(30,a),g); | ||
| − | + | strcpy(s,""); | |
| − | + | strcat(s, "o2.txt"); | |
| − | + | outfile.open(s,ios :: trunc); | |
| − | + | outfile.close(); | |
| − | + | Vector3D r1 = b2.MR1(dt),rp; | |
| − | + | for (double i = 0; i <= 20; i += dt) | |
| − | + | { | |
| − | + | rp = b2.getR(); | |
| − | + | b2.writePosToFile(s); | |
| − | + | b2.writePosToScreen(); | |
| − | + | b2.changeR(r1,dt); | |
| − | + | b2.changeV(r1,dt); | |
| − | + | r1.x = rp.x; | |
| − | + | r1.y = rp.y; | |
| − | + | } | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | //Точное решение (Линейная зависимость) | |
| − | + | dt = 0.1; | |
| + | a = (M_PI * 30)/180; | ||
| + | Ball b3(a,10 , 1, MakeVector(0,0,0),MakeVector(30,a),g); | ||
| − | + | strcpy(s,""); | |
| − | + | strcat(s, "o3.txt"); | |
| − | + | outfile.open(s, ios :: trunc); | |
| − | + | outfile.close(); | |
| + | for (double i = 0; i <= 20; i += dt) | ||
| + | { | ||
| + | b3.WVTS(b3.positionReal(i)); | ||
| + | b3.WVTF(b3.positionReal(i), s); | ||
| + | } | ||
| − | |||
| − | |||
| − | + | //Верле (Квадратичная зависимость) | |
| − | + | dt = 0.1; | |
| − | + | a = (M_PI * 30)/180; | |
| − | + | Ball b4(a,10 , 1, MakeVector(0,0,0),MakeVector(30,a),g); | |
| − | |||
| − | |||
| − | |||
| − | + | strcpy(s,""); | |
| − | + | strcat(s, "o4.txt"); | |
| − | + | outfile.open(s, ios :: trunc); | |
| − | + | outfile.close(); | |
| − | + | r1 = b4.MR1(dt); | |
| − | + | for (double i = 0; i <= 20; i += dt) | |
| − | + | { | |
| − | + | rp = b4.getR(); | |
| − | + | b4.writePosToFile(s); | |
| − | + | b4.writePosToScreen(); | |
| − | + | b4.changeRSQ(r1,dt); | |
| − | + | b4.changeV(r1,dt); | |
| − | + | r1.x = rp.x; | |
| − | + | r1.y = rp.y; | |
| − | + | } | |
| − | + | ||
| − | + | return 0; | |
| − | |||
} | } | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | Файл "'''Vector.h'''" | ||
| + | <syntaxhighlight lang="cpp" line start="1" enclose="div"> | ||
| + | #ifndef VECTOR_H_INCLUDED | ||
| + | #define VECTOR_H_INCLUDED | ||
| − | + | struct Vector3D | |
{ | { | ||
| − | + | double x,y,z; | |
| + | }; | ||
| − | + | Vector3D VmV(Vector3D v1,Vector3D v2) //векторное вычитание | |
| − | + | { | |
| − | + | Vector3D v = {v1.x - v2.x,v1.y - v2.y,v1.z - v2.z }; | |
| − | + | return v; | |
| − | + | }; | |
| − | + | Vector3D VpV(Vector3D v1,Vector3D v2) //векторное сложение | |
| − | + | { | |
| − | + | Vector3D v = {v1.x + v2.x,v1.y + v2.y,v1.z + v2.z }; | |
| − | + | return v; | |
| − | + | } | |
| − | |||
| − | + | double VV(Vector3D v1,Vector3D v2) //скалярное умножение | |
| − | + | { | |
| − | + | return (v1.x*v2.x + v1.y*v2.y + v1.z*v2.z); | |
| − | + | } | |
| − | |||
| − | |||
| − | + | Vector3D VxV(Vector3D v1,Vector3D v2) //векторное умножение | |
| + | { | ||
| + | Vector3D v = {v1.y*v2.z - v1.z*v2.y, v1.z*v2.x - v1.x*v2.z,v1.x*v2.y - v1.y*v2.x}; | ||
| + | return v; | ||
} | } | ||
| − | |||
| − | |||
| − | |||
| − | + | bool Kol(Vector3D v1,Vector3D v2) | |
| + | { | ||
| + | return ((v1.x/v2.x == v1.y/v2.y)&&(v1.z/v2.z == v1.y/v2.y))? true:false; | ||
| + | } | ||
| − | + | Vector3D VS(Vector3D v1, double s) | |
| − | + | { | |
| − | + | Vector3D v = {v1.x*s, v1.y*s, v1.z*s}; | |
| − | + | return v; | |
| − | + | } | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | double Length(Vector3D v1) | ||
| + | { | ||
| + | return sqrt(VV(v1,v1)); | ||
| + | } | ||
| − | + | Vector3D MakeVector(double x,double y,double z) | |
| − | + | { | |
| − | + | Vector3D v = {x,y,z}; | |
| − | + | return v; | |
} | } | ||
| − | </syntaxhighlight> | + | Vector3D MakeVector(double length,double angle) |
| + | { | ||
| + | Vector3D v = {length * cos(angle), length * sin(angle),0}; | ||
| + | return v; | ||
| + | } | ||
| + | |||
| + | double Proection(Vector3D base, Vector3D dir) | ||
| + | { | ||
| + | return (VV(base,dir)/Length(base)); | ||
| + | } | ||
| + | #endif // VECTOR_H_INCLUDED | ||
| + | </syntaxhighlight> | ||
</div> | </div> | ||
| − | |||
| − | <div | + | <div> |
| − | '''[[ | + | '''[[Лобанов Илья]]''' |
| − | '''Описание программы''': программа записывает в четыре файла результаты вычисления: | + | '''Описание программы''' : программа записывает в четыре файла результаты вычисления: |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Координаты, рассчитанные по формуле, при движении без сопротивления воздуха; | |
| + | Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости; | ||
| + | Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости; | ||
| + | Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости. | ||
| − | |||
| − | |||
| − | + | '''Краткая инструкция''': | |
| + | В окне консоли пользователю предлагается вывести следующие значения: начальную скорость , угол и шаг. | ||
| + | После этого полученные в результате работы программы данные выводятся в файл. | ||
| + | Скачивать [[http://tm.spbstu.ru/File:Air.rar тут]] | ||
| + | [[http://tm.spbstu.ru/File:phys.rar тут]] | ||
| + | |||
| + | </div> | ||
| + | |||
| + | <div class="mw-collapsible mw-collapsed" style="width:100%" > | ||
| + | '''[[Лосева Татьяна ]]''' | ||
| + | |||
| + | '''Описание:''' Пользователя попросят ввести начальную скорость,угол бросания,массу тела и коэф.сопротивления воздуха,тогда программа запишет в 4 разных файла результаты следующих вычислений: | ||
| + | # Координаты, рассчитанные по формуле, при движении без сопротивления воздуха; | ||
| + | # Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости; | ||
| + | # Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости. | ||
| + | # Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости; | ||
| + | |||
| + | <div class="mw-collapsible-content"> | ||
| + | |||
| + | ''Графики полученные при скорости =10 m/c;угле = 30 градусам;массе=10 кг;коэф.сопротивления=1;'' | ||
| + | |||
| + | [[File:загружено (1).png]][[:File:загружено (1).png]] | ||
| − | |||
<syntaxhighlight lang="cpp" line start="1" enclose="div"> | <syntaxhighlight lang="cpp" line start="1" enclose="div"> | ||
| − | #include <iostream> | + | #include<iostream> |
| − | # | + | using namespace std; |
| − | # | + | #define N 1 |
| + | #define PI 3.14159265 | ||
#include <fstream> | #include <fstream> | ||
| − | #include< | + | #include<cmath> |
| − | #include < | + | double g=9.8; |
| − | + | double step=0.01; | |
| − | + | #include<math.h> | |
| + | |||
| + | void Func(double v,double r)//1.Координаты, рассчитанные по формуле, при движении без сопротивления воздуха; | ||
| + | |||
{ | { | ||
| − | + | double x,y; | |
| − | + | ||
| − | double x,y | + | ofstream fout;//открытие файла |
| − | + | fout.open("C:\\Users\\Light\\Desktop\\1.txt");//указываем путь записи | |
| − | + | cout<<"method1"<<endl; | |
| − | + | ||
| − | + | for(double t=0.01;t<N;t=t+0.01) | |
| − | + | { | |
| − | + | y=v*t*sin(r*PI/ 180)-g*t*t/2;//координата y | |
| − | { | + | x=v*t*cos(r*PI / 180);//координата х |
| − | + | ||
| − | + | fout<<x<<" ";//запись в файл х | |
| − | + | cout<<"X="<<x<<endl;//вывод на экран | |
| − | + | fout<<y<<" ";//запись в файл | |
| − | + | cout<<"Y="<<y<<endl<<endl;//вывод на экран | |
| + | fout<<endl; | ||
| + | } | ||
} | } | ||
| − | + | ||
| − | + | void Verle1( double n,double m ,double v0,double r)//Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости; | |
| − | + | ||
| − | + | { | |
| − | + | double x,y,x0=0,y0=0,xn_1,yn_1;//x0,y0=Xn,Yn начальные значения;xn_1=X(n-1);yn_1=Y(n-1); | |
| − | + | ||
| − | + | double vx=v0*cos(r*PI / 180);//рассчитваем Vn для первого случая n=0 для x | |
| − | + | double vy=v0*sin(r*PI/ 180)-g*step;//рассчитваем Vn для первого случая n=0 для y | |
| − | + | ||
| − | + | xn_1=x0-vx*step;//X(n-1) для первого случая n=0 | |
| − | + | yn_1=y0-vy*step;//Y(n-1) для первого случая n=0 | |
| − | + | ofstream fout;//открытие файла | |
| − | + | fout.open("C:\\Users\\Light\\Desktop\\2.txt");//путь записи в файл | |
| − | + | cout<<"Verle1"<<endl<<endl; | |
| − | + | for(double t=0.02;t<N;t=t+step) | |
| − | + | { | |
| − | + | x=2*x0-xn_1-(n*vx*step*step)/m;//считаем Хn+1 | |
| − | + | vx=(x-xn_1)/(2*step); | |
| − | + | xn_1=x0;//для следущего шага Xn-1=Xn | |
| − | + | x0=x;//для следущего шага Xn=Xn+1 | |
| − | + | ||
| − | + | y=2*y0-yn_1-(g+(n*vy)/m)*step*step;//Yn+1 | |
| − | + | vy=(y-yn_1)/(2*0.01);//скорость | |
| − | + | yn_1=y0;//для следущего шага Yn-1=Yn | |
| − | + | y0=y;//для следущего шага Yn=Yn+1 | |
| − | + | cout<<"X="<<x<<endl; | |
| − | + | cout<<"Y="<<y<<endl<<endl; | |
| − | + | fout<<x<<" "; | |
| − | + | fout<<y<<" "; | |
| − | + | fout<<endl; | |
| − | + | ||
| − | + | ||
| − | + | } | |
| − | + | } | |
| − | + | ||
| − | + | void Verle2( double n,double m ,double v0,double r)//3.Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости. | |
| − | + | ||
| − | + | { | |
| − | + | double x,y,x0=0,y0=0,xn_1,yn_1,v;//x0,y0=Xn,Yn начальные значения;xn_1=X(n-1);yn_1=Y(n-1); | |
| − | + | ||
| − | + | double vx=v0*cos(r*PI / 180);//рассчитваем Vn для первого случая n=0 для x | |
| − | + | double vy=v0*sin(r*PI/ 180)-g*step;//рассчитваем Vn для первого случая n=0 для y | |
| − | + | ||
| − | + | xn_1=x0-vx*step;//X(n-1) для первого случая n=0 | |
| − | + | yn_1=y0-vy*step;//Y(n-1) для первого случая n=0 | |
| − | + | ofstream fout;//открытие файла | |
| − | + | fout.open("C:\\Users\\Light\\Desktop\\3.txt");//путь записи | |
| − | + | cout<<"Verle2"<<endl<<endl; | |
| − | + | for(double t=0.02;t<N;t=t+step) | |
| − | + | { | |
| − | + | ||
| − | + | v=sqrt(vx*vx+vy*vy);//скорость V | |
| − | + | ||
| − | + | x=2*x0-xn_1-(n*v*vx*step*step)/m;//Xn+1 | |
| − | + | vx=(x-xn_1)/(2*step);//скорость Vx | |
| − | + | xn_1=x0;//для следущего шага Xn-1=Xn | |
| − | + | x0=x;//для следущего шага Xn=Xn+1 | |
| − | + | ||
| − | + | y=2*y0-yn_1-(g+(n*vy*v)/m)*step*step;//Yn+1 | |
| − | + | vy=(y-yn_1)/(2*0.01);//скорость Vy | |
| − | + | yn_1=y0;//для следущего шага Yn-1=Yn | |
| − | + | y0=y;//для следущего шага Yn=Yn+1 | |
| − | + | cout<<"X="<<x<<endl; | |
| − | + | cout<<"Y="<<y<<endl<<endl; | |
| − | + | fout<<x<<" "; | |
| − | + | fout<<y<<" "; | |
| − | + | fout<<endl; | |
| − | + | } | |
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
} | } | ||
| − | </ | + | void method4(double n,double m ,double v0,double r)//Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости; |
| − | < | + | { |
| + | double x,y,x0=0,y0=0;//x0,y0 начальные значения; | ||
| + | |||
| + | double vx=v0*cos(r*PI / 180);//рассчитваем Vx | ||
| + | double vy=v0*sin(r*PI/ 180)-g*step;//рассчитваем Vy | ||
| + | |||
| + | ofstream fout;//открытие файла | ||
| + | fout.open("C:\\Users\\Light\\Desktop\\4.txt"); | ||
| + | cout<<"4"<<endl<<endl; | ||
| + | for(double t=0.01;t<N;t=t+step) | ||
| + | { | ||
| + | x=x0+m*vx*(1-(exp((-1*n)*t/m)))/n;//координата х | ||
| + | |||
| + | y = y0+(m/n)*((vy + g * m / n)*(1 - exp(-1 * n * t / m))) - g * t*m/n;//координата у | ||
| + | |||
| + | //вывод в файл и на экран | ||
| + | cout<<"X="<<x<<endl; | ||
| + | cout<<"Y="<<y<<endl<<endl; | ||
| + | fout<<x<<" "; | ||
| + | fout<<y<<" "; | ||
| + | fout<<endl; | ||
| + | } | ||
| + | } | ||
| + | |||
| + | int main(void) | ||
| + | { | ||
| − | < | + | double v0,r,m,n;//v0-начальная скорость,r-угол в градусах,m-масса;n-коэф.сопротивления ветра |
| − | + | ||
| + | cout<<"Enter start speed:"<<endl; | ||
| + | cin>>v0; | ||
| + | cout<<"Enter angle less than 90 deg:"<<endl; | ||
| + | cin>>r; | ||
| + | cout<<"Enter mass:"<<endl; | ||
| + | cin>>m; | ||
| + | cout<<"Coefficient of resistance:"<<endl; | ||
| + | cin>>n; | ||
| + | |||
| + | Func(v0,r); | ||
| + | Verle1(n,m,v0,r); | ||
| + | Verle2(n,m,v0,r); | ||
| + | method4(n,m,v0,r); | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | int k; | ||
| + | cin>>k; | ||
| + | return 0; | ||
| + | } | ||
| − | + | </syntaxhighlight> | |
| − | + | </div> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Скачать можно [http://tm.spbstu.ru/Файл:Verle.rar тут]. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | <div> | ||
| − | + | '''[[Ляжков Сергей]]''' | |
| + | '''Описание программы''': Программа рассчитывает координаты полета тела по х и у. Как и в программе шахмат и интерполяции, здесь представлено меню выбора функций. Вы вводите начальные координаты, начальную скорость и угол полета(например, мяча или снаряда)(Нет смысла вводить величину скорости света, так как парабола вряд ли получится). | ||
| + | Затем Вы выбираете в меню "вариант" сопротивления воздуха, после чего вводите массу тела и коэффициент сопротивления среды(без сопротивления воздуха этим можно пренебречь). Программа выводит массив точек и сохраняет их в текстовый файл. Эти точки - координаты полета до тех пор, пока значения y не станет ОТРИЦАТЕЛЬНЫМИ... | ||
| + | Это мой первый проект по моделированию, спасибо за предоставленную возможность попрактиковаться. | ||
| + | Скачать можно [[http://mech.spbstu.ru/File:Полет.zip тут]] | ||
| + | </div> | ||
| − | + | <br>'''[[Нарядчиков Александр]]'''<br> | |
| − | + | '''Инструкция:''' Пользователю достаточно просто запустить программу.<br> | |
| − | + | '''Описание программы:''' В комнате скачут 4 мячика, первый двигается без сопротивления воздуха, второй двигается с квадратичной зависимостью сопротивления воздуха от скорости (Метод Верле), третий двигается с линейной зависимостью сопротивления воздуха от скорости (точное решение), четвертый двигается с линейной зависимостью сопротивления воздуха от скорости (Метод Верле).<br> | |
| − | + | '''Описание алгоритма:''' Программа реализована с помощью системы анимации(class anim), используя библиотеки OpenGl и GLUT. Изменения координат мячей проходят в режиме реального времени в векторной форме.<br> | |
| − | + | <div class="mw-collapsible mw-collapsed" style="width:100%" > | |
| − | + | "'''T06BALL.CPP'''" | |
| − | + | <syntaxhighlight lang="cpp" line start="1" enclose="div"> | |
| − | + | /* FILENAME: T06BALL.CPP | |
| − | + | * LAST UPDATE: 17.01.2016 | |
| − | + | */ | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | #include "ANIM.H" | ||
| + | #include "SAMPLE.H" | ||
| − | + | /* Main function */ | |
| − | + | void main( void ) | |
| − | |||
| − | |||
| − | |||
{ | { | ||
| − | + | // Получение единственного экземпляра класса анимации | |
| − | + | sagl::anim &My = sagl::anim::Get(); | |
| − | + | ||
| − | + | // Шар, летящий без сопротивлением воздуха | |
| − | + | for (int i = 0; i < 1; i++) | |
| − | + | My << new ball(Pi / 6, 10 + i); | |
| − | |||
| + | // Шар, летящий с сопротивлением воздуха | ||
| + | // Координаты получены методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости | ||
| + | for (int i = 0; i < 1; i++) | ||
| + | My << new ball_air(Pi / 6, 10 + i, 10, 0.01); | ||
| − | + | // Шар, летящий с сопротивлением воздуха | |
| − | + | // Координаты получены из точного решения при линейной зависимости силы сопротивлении воздуха от скорости | |
| − | + | for (int i = 0; i < 1; i++) | |
| − | + | My << new ball_air_2(Pi / 6, 10 + i, 10, 0.01); | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | // Шар, летящий с сопротивлением воздуха | |
| − | + | // Координаты получены методом Верле при линейной зависимости силы сопротивлении воздуха от скорости | |
| − | + | for (int i = 0; i < 1; i++) | |
| − | + | My << new ball_air_3(Pi / 6, 10 + i, 10, 0.01); | |
| − | + | ||
| − | + | // Запуск главного цикла | |
| + | My.Run(); | ||
| + | } // End of 'main' function | ||
| − | + | // END OF 'T43ANIM.CPP' FILE | |
| − | + | </syntaxhighlight> | |
| − | + | "'''ANIM.CPP'''" | |
| − | + | <syntaxhighlight lang="cpp" line start="1" enclose="div"> | |
| − | + | /* FILENAME: ANIM.CPP | |
| + | * LAST UPDATE: 17.01.2016 | ||
| + | */ | ||
| − | + | #include <stdio.h> | |
| + | #include <stdlib.h> | ||
| + | #include <time.h> | ||
| − | + | #include "ANIM.H" | |
| + | // Единственный экземпляр класса | ||
| + | sagl::anim sagl::anim::Instance; | ||
| − | int | + | /* Reshape function */ |
| + | // Стандартная функция, вызываемая при изменении размеров окна | ||
| + | void sagl::anim::Reshape( int W, int H ) | ||
{ | { | ||
| − | + | // Установка области просмотра - все окно | |
| − | + | glViewport(0, 0, W, H); | |
| − | + | Instance.WinW = W; | |
| − | + | Instance.WinH = H; | |
| − | + | double ratio_x = 1, ratio_y = 1; | |
| − | + | if (W > H) | |
| − | + | ratio_x = (double)W / H; | |
| + | else | ||
| + | ratio_y = (double)H / W; | ||
| + | double Size = 1, Near = 1, Far = 500; | ||
| + | // Установка системы координат "камеры" | ||
| + | glMatrixMode(GL_PROJECTION); | ||
| + | glLoadIdentity(); | ||
| + | glFrustum(-Size * ratio_x, Size * ratio_x, | ||
| + | -Size * ratio_y, Size * ratio_y, | ||
| + | Near, Far); | ||
| + | // Установка "мировой" СК в состояние без преобразований | ||
| + | glMatrixMode(GL_MODELVIEW); | ||
| + | } // End of 'Reshape' function | ||
| + | /* Timer function */ | ||
| + | // Подсчет времени | ||
| + | void sagl::anim::Timer( void ) | ||
| + | { | ||
| + | long Time = clock(); | ||
| + | |||
| + | if (IsPause) | ||
| + | DeltaTime = 0, PauseTime += Time - OldTime; | ||
| + | else | ||
| + | DeltaTime = (Time - OldTime) / (double)CLOCKS_PER_SEC; | ||
| + | OldTime = Time; | ||
| − | + | SyncTime = (Time - PauseTime - StartTime) / (double)CLOCKS_PER_SEC; | |
| − | + | } /* End of 'Timer' function */ | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | /* Display function */ | |
| − | + | // Стандартная функция, вызываемая при перерисовке окна | |
| − | + | void sagl::anim::Display( void ) | |
| − | + | { | |
| − | + | // Запуск времени | |
| − | + | Instance.Timer(); | |
| + | // Очищаем цветовой буфер для создания нового изображения | ||
| + | glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); | ||
| + | glLoadIdentity(); | ||
| + | // Позиционирование СК | ||
| + | gluLookAt(-40, 0, 0, 0, 0, 0, 0, 1, 0); | ||
| − | + | // Отрисовка объектов | |
| − | + | Instance.Render(); | |
| − | |||
| − | |||
| − | |||
| − | + | glFinish(); | |
| + | // Копируем вторичный буфер в окно | ||
| + | glutSwapBuffers(); | ||
| + | // Вызываем функцию обновления кадра | ||
| + | glutPostRedisplay(); | ||
| + | } // End of 'Display' function | ||
| − | } | + | /* Keyboard function */ |
| + | // Стандартная функция, вызываемая при нажатие клавиш на клавиатуре | ||
| + | void sagl::anim::Keyboard( unsigned char Key, int X, int Y ) | ||
| + | { | ||
| + | // Выход из программы | ||
| + | if (Key == 27) | ||
| + | exit(0); | ||
| + | // Открытие программы в полном экране | ||
| + | else if (Key == 'f') | ||
| + | glutFullScreen(); | ||
| + | // Пауза | ||
| + | else if (Key == 'p' || Key == 'P') | ||
| + | Instance.IsPause = !Instance.IsPause; | ||
| + | } // End of 'Keyboard' function | ||
| − | + | sagl::anim::anim( void ) : IsPause(false), SyncTime(0), DeltaTime(0), | |
| − | + | StartTime(clock()), OldTime(StartTime), PauseTime(0), StockSize(0) | |
{ | { | ||
| + | // Инициализации OpenGL и GLUT | ||
| + | glutInitDisplayMode(GLUT_RGB | GLUT_DOUBLE | GLUT_DEPTH); | ||
| + | |||
| + | // Задача размеров и позиции окна | ||
| + | glutInitWindowPosition(0, 0); | ||
| + | glutInitWindowSize(700, 700); | ||
| + | // Создание окна | ||
| + | glutCreateWindow("T06BALL"); | ||
| − | + | // Установка функций 'обратного вызова' | |
| − | + | glutDisplayFunc(Display); | |
| − | + | glutKeyboardFunc(Keyboard); | |
| − | + | glutReshapeFunc(Reshape); | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | // Установка цвета закраски фона | |
| − | + | glClearColor(0.3, 0.5, 0.7, 1); | |
| − | + | // Включение буфера глубины | |
| − | + | glEnable(GL_DEPTH_TEST); | |
| − | + | // Включение режима вычисления цвета согласно освещенности от источников света | |
| − | + | glEnable(GL_LIGHTING); | |
| − | + | // Включение источника света | |
| − | + | glEnable(GL_LIGHT0); | |
| − | + | // Включение упрощенного режима освещенности для простого способа описания свойств поверхности | |
| − | + | glEnable(GL_COLOR_MATERIAL); | |
| − | + | // Приведение нормалей к единичной длине | |
| − | + | glEnable(GL_NORMALIZE); | |
| − | + | } | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | // Деструктор | |
| + | sagl::anim::~anim( void ) | ||
| + | { | ||
| + | // Чистка памяти | ||
| + | for (int i = 0; i < StockSize; i++) | ||
| + | delete Stock[i]; | ||
} | } | ||
| + | /* Render function */ | ||
| + | // Отрисовка объектов | ||
| + | void sagl::anim::Render( void ) | ||
| + | { | ||
| + | for (int i = 0; i < StockSize; i++) | ||
| + | Stock[i]->Render(*this); | ||
| + | } // End of 'Render' function | ||
| − | + | /* Run function */ | |
| − | + | // Запуск главного цикла | |
| + | void sagl::anim::Run( void ) | ||
| + | { | ||
| + | // Запуск основного цикла построения | ||
| + | glutMainLoop(); | ||
| + | } // End of 'Run' function | ||
| + | // END OF 'ANIM.CPP' FILE | ||
| + | </syntaxhighlight> | ||
| + | "'''ANIM.H'''" | ||
| + | <syntaxhighlight lang="cpp" line start="1" enclose="div"> | ||
| + | /* FILENAME: ANIM.H | ||
| + | * LAST UPDATE: 17.01.2016 | ||
| + | */ | ||
| − | + | #ifndef __ANIM_H_ | |
| − | + | #define __ANIM_H_ | |
| − | + | #include <stdio.h> | |
| − | + | #include <stdlib.h> | |
| − | # | + | #include <time.h> |
| − | # | ||
| − | |||
| − | |||
| − | + | #include <GL\glut.h> | |
| − | + | #include "VEC.H" | |
| − | + | // Константы | |
| − | + | #define Pi 3.14159265358979323846 | |
| + | #define E 2.71828182845904523536 | ||
| − | + | // Собственное пространство имен 'sagl' | |
| − | + | namespace sagl | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{ | { | ||
| − | + | // Объявления класса анимации наперед | |
| − | + | class anim; | |
| − | + | ||
| − | + | // Функции получения случайных чисел | |
| − | + | inline double r0( void ) | |
| − | + | { | |
| − | + | return rand() / (double)RAND_MAX; | |
| − | + | } | |
| − | / | + | inline double r1( void ) |
| − | + | { | |
| − | + | return 2.0 * rand() / RAND_MAX - 1; | |
| − | + | } | |
| − | + | ||
| − | + | // Класс объектов | |
| − | + | class object | |
| − | // | + | { |
| − | + | public: | |
| − | + | // Вектора перемещения и скоростей | |
| − | // | + | vec P, V, AbsV; |
| − | + | ||
| − | + | // Конструктор | |
| − | + | object( void ) : P(vec::Rnd1()), V(vec::Rnd()), AbsV(V) | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{ | { | ||
| − | |||
| − | |||
} | } | ||
| − | + | ||
| − | + | // Отрисовка объектов | |
| − | + | virtual void Render( anim &Ani ) | |
| − | + | { | |
| − | + | } // End of 'Render' function | |
| − | + | }; // end of 'object' class | |
| − | + | ||
| + | // Класс анимации | ||
| + | class anim | ||
| + | { | ||
| + | private: | ||
| + | // Функции 'обратного вызова' | ||
| + | static void Display( void ); | ||
| + | static void Keyboard( unsigned char Key, int X, int Y ); | ||
| + | static void Reshape( int W, int H ); | ||
| − | + | // Единственный экземпляр класса | |
| − | + | static anim Instance; | |
| − | + | ||
| − | + | // Конструктор | |
| − | + | anim( void ); | |
| − | |||
| − | + | // Максимальное количество объектов | |
| − | + | static const int Max = 100; | |
| − | + | // 'Контейнер' объектов | |
| − | // | + | object *Stock[Max]; |
| − | + | // Размер 'контейнера' объектов | |
| − | + | int StockSize; | |
| − | + | ||
| − | + | // Переменные, хранящие время в секундах | |
| + | long StartTime, OldTime, PauseTime; | ||
| + | |||
| + | // Отрисовка объектов | ||
| + | void Render( void ); | ||
| + | |||
| + | // Подсчет времени | ||
| + | void Timer( void ); | ||
| + | public: | ||
| + | // Добавление объектов в 'контейнер' | ||
| + | anim & operator<<( object *Obj ) | ||
| + | { | ||
| + | if (StockSize < Max ) | ||
| + | Stock[StockSize++] = Obj; | ||
| + | else | ||
| + | delete Obj; | ||
| + | |||
| + | return *this; | ||
| + | } | ||
| + | |||
| + | // Ширина и высота окна | ||
| + | int WinW, WinH; | ||
| − | + | // Переменные, хранящие время в секундах | |
| − | + | double SyncTime, DeltaTime; | |
| − | |||
| − | // | + | // Переменная, отвечающая за паузу |
| + | bool IsPause; | ||
| − | + | // Деструктор | |
| − | + | ~anim( void ); | |
| + | |||
| + | // Запуск главного цикла | ||
| + | void Run( void ); | ||
| + | |||
| + | // Метод, возвращающий переменную - единственный экземпляр данного типа | ||
| + | static anim & Get( void ) | ||
| + | { | ||
| + | return Instance; | ||
| + | } | ||
| + | }; // end of 'anim' class | ||
| + | } // end of 'sagl' namespace | ||
| − | + | #endif /*__ANIM_H_ */ | |
| − | |||
| − | |||
| − | |||
| − | + | // END OF 'ANIM.H' FILE | |
| − | + | </syntaxhighlight> | |
| + | "'''VEC.H'''" | ||
| + | <syntaxhighlight lang="cpp" line start="1" enclose="div"> | ||
| + | /* FILENAME: VEC.H | ||
| + | * LAST UPDATE: 17.01.2016 | ||
| + | */ | ||
| − | + | #ifndef __VEC_H_ | |
| + | #define __VEC_H_ | ||
| − | + | #include <stdlib.h> | |
| − | + | #include <math.h> | |
| − | |||
| − | |||
| − | + | // Собственное пространство имен 'sagl' | |
| − | + | namespace sagl | |
| − | + | { | |
| − | + | // Класс векторов | |
| − | + | class vec | |
| − | + | { | |
| − | + | public: | |
| − | + | // Координаты вектора | |
| − | + | double X, Y, Z; | |
| − | + | ||
| + | // Конструктор | ||
| + | vec( void ) : X(0), Y(0), Z(0) | ||
{ | { | ||
| − | |||
| − | |||
| − | |||
| − | |||
} | } | ||
| − | + | ||
| − | + | // Конструктор | |
| − | + | vec( double A, double B, double C ) : X(A), Y(B), Z(C) | |
| − | |||
| − | |||
| − | |||
{ | { | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
} | } | ||
| − | + | ||
| − | + | // Функции получения случайных чисел | |
| − | + | static double R0( void ) | |
| − | + | { | |
| − | + | return rand() / (double)RAND_MAX; | |
| − | + | } | |
| + | |||
| + | static double R1( void ) | ||
{ | { | ||
| − | + | return 2 * rand() / (double)RAND_MAX - 1; | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
} | } | ||
| − | + | ||
| − | + | // Функции получения случайных векторов | |
| − | + | static vec Rnd( void ) | |
| − | + | { | |
| − | + | return vec(R0(), R0(), R0()); | |
| − | + | } | |
| + | |||
| + | static vec Rnd1( void ) | ||
{ | { | ||
| − | + | return vec(R1(), R1(), R1()); | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
} | } | ||
| − | + | ||
| − | + | vec operator+( vec V ) | |
| − | + | { | |
| − | + | return vec(X + V.X, Y + V.Y, Z + V.Z); | |
| − | + | } | |
| − | } | + | |
| − | + | vec operator*( double t ) | |
| − | + | { | |
| − | + | return vec(X * t, Y * t, Z * t); | |
| − | + | } | |
| − | ''' | + | |
| + | vec & operator+=( const vec &V ) | ||
| + | { | ||
| + | X += V.X; | ||
| + | Y += V.Y; | ||
| + | Z += V.Z; | ||
| + | |||
| + | return *this; | ||
| + | } | ||
| + | |||
| + | // Длина вектора | ||
| + | double operator!(void) const | ||
| + | { | ||
| + | return sqrt(X * X + Y * Y + Z * Z); | ||
| + | } /* end of 'operator!' function */ | ||
| + | }; // end of 'vec' class | ||
| + | } // end of 'sagl' namespace | ||
| − | + | #endif /*__VEC_H_ */ | |
| − | # | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | // END OF 'VEC.H' FILE | ||
| + | </syntaxhighlight> | ||
| + | "'''SAMPLE.H'''" | ||
<syntaxhighlight lang="cpp" line start="1" enclose="div"> | <syntaxhighlight lang="cpp" line start="1" enclose="div"> | ||
| − | + | /* FILENAME: SAMPLE.H | |
| − | + | * LAST UPDATE: 17.01.2016 | |
| − | + | */ | |
| − | + | #ifndef __SAMPLE_H_ | |
| + | #define __SAMPLE_H_ | ||
| − | + | #include <math.h> | |
| − | + | #include "ANIM.H" | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | // Шар, летящий без сопротивлением воздуха | |
| + | class ball : public sagl::object | ||
{ | { | ||
| − | + | private: | |
| − | + | double angle, v; // угол вектора скорости к горизонту; модуль скорости | |
| − | + | public: | |
| − | + | // Конструктор | |
| − | + | ball( void ) : angle(Pi / 3), v(1) | |
| − | + | { | |
| − | + | P = sagl::vec(sagl::r0() + 5, 5, 0); | |
| − | + | V.X = 0; | |
| − | + | V.Y = sin(angle) * v; | |
| − | + | V.Z = cos(angle) * v; | |
| − | + | } | |
| − | + | ||
| − | + | // Конструктор | |
| − | + | ball( double angle1, double v1 ) : angle(angle1), v(v1) | |
| − | + | { | |
| − | + | P = sagl::vec(sagl::r0() + 5, 5, 0); | |
| − | + | V.X = 0; | |
| − | + | V.Y = sin(angle) * v; | |
| − | + | V.Z = cos(angle) * v; | |
| − | + | } | |
| − | + | ||
| − | + | // Отрисовка объекта | |
| − | + | void Render( sagl::anim &Ani ) | |
| − | + | { | |
| − | + | // Вектор ускорения свободного падения | |
| − | + | sagl::vec g = sagl::vec(0, -9.8, 0); | |
| + | // Размер комнаты | ||
| + | double Size = 120; | ||
| − | + | // Изменение вектора скорости | |
| − | + | V += g * Ani.DeltaTime; | |
| − | + | // Изменение вектора перемещения | |
| − | + | P += V * Ani.DeltaTime; | |
| − | + | // Ограничения - стенки | |
| − | + | if (P.X > Size / 4) | |
| − | + | V.X = -fabs(V.X); | |
| − | + | if (P.X < -Size / 4) | |
| + | V.X = fabs(V.X); | ||
| − | + | if (P.Y > Size / 4) | |
| − | + | V.Y = -fabs(V.Y); | |
| − | + | if (P.Y < -Size / 4) | |
| − | + | V.Y = fabs(V.Y); | |
| − | + | if (P.Z > Size / 4) | |
| − | + | V.Z = -fabs(V.Z); | |
| − | + | if (P.Z < -Size / 4) | |
| − | + | V.Z = fabs(V.Z); | |
| − | + | ||
| − | + | // Запоминание состояния изменения текущей СК | |
| − | + | glPushMatrix(); | |
| − | } | + | |
| + | // Рисование стенок | ||
| + | glutWireCube(Size / 2); | ||
| + | // Задача перемещения мяча | ||
| + | glTranslated(P.X, P.Y, P.Z); | ||
| + | // Цвет мяча | ||
| + | glColor3d(0, 1, 0); | ||
| + | // Рисование мяча | ||
| + | glutSolidSphere(0.5, 30, 30); | ||
| + | |||
| + | // Восстановление последнего запоминания состояния изменения текущей СК | ||
| + | glPopMatrix(); | ||
| + | } | ||
| + | }; // end of 'ball' class | ||
| − | + | // Шар, летящий с сопротивлением воздуха | |
| + | // Координаты получены методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости | ||
| + | class ball_air : public sagl::object | ||
{ | { | ||
| − | + | private: | |
| − | + | double angle, v, m, n; | |
| − | + | public: | |
| − | + | // Конструктор | |
| − | + | ball_air( void ) : angle(Pi / 3), v(1), m(1), n(0.1) | |
| − | + | { | |
| − | + | P = sagl::vec(sagl::r0() + 5, 5, 0); | |
| + | V.X = 0; | ||
| + | V.Y = sin(angle) * v; | ||
| + | V.Z = cos(angle) * v; | ||
| + | } | ||
| + | |||
| + | // Конструктор | ||
| + | ball_air( double angle1, double v1, double m1, double n1 ) : angle(angle1), v(v1), m(m1), n(n1) | ||
| + | { | ||
| + | P = sagl::vec(sagl::r0() + 5, 5, 0); | ||
| + | V.X = 0; | ||
| + | V.Y = sin(angle) * v; | ||
| + | V.Z = cos(angle) * v; | ||
| + | } | ||
| + | |||
| + | // Отрисовка объекта | ||
| + | void Render( sagl::anim &Ani ) | ||
| + | { | ||
| + | // Вектор ускорения свободного падения и вектор полного ускорения | ||
| + | sagl::vec g = sagl::vec(0, -9.8, 0), a; | ||
| + | // Размер комнаты | ||
| + | double Size = 120; | ||
| + | |||
| + | // Изменение вектора ускорения | ||
| + | a = sagl::vec(0, g.Y - n / m * !V * V.Y, -n / m * !V * V.Z); | ||
| + | |||
| + | // Изменение вектора скорости | ||
| + | V += a * Ani.DeltaTime; | ||
| + | // Изменение вектора перемещения | ||
| + | P += V * Ani.DeltaTime; | ||
| − | + | // Ограничения - стенки | |
| − | + | if (P.X > Size / 4) | |
| − | + | V.X = -fabs(V.X); | |
| − | + | if (P.X < -Size / 4) | |
| − | + | V.X = fabs(V.X); | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | if (P.Y > Size / 4) | |
| − | + | V.Y = -fabs(V.Y); | |
| − | + | if (P.Y < -Size / 4) | |
| − | + | V.Y = fabs(V.Y); | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | if (P.Z > Size / 4) | |
| + | V.Z = -fabs(V.Z); | ||
| + | if (P.Z < -Size / 4) | ||
| + | V.Z = fabs(V.Z); | ||
| + | |||
| + | // Запоминание состояния изменения текущей СК | ||
| + | glPushMatrix(); | ||
| + | |||
| + | // Рисование стенок | ||
| + | glutWireCube(Size / 2); | ||
| + | // Задача перемещения мяча | ||
| + | glTranslated(P.X, P.Y, P.Z); | ||
| + | // Цвет мяча | ||
| + | glColor3d(1, 0, 0); | ||
| + | // Рисование мяча | ||
| + | glutSolidSphere(0.5, 30, 30); | ||
| + | |||
| + | // Восстановление последнего запоминания состояния изменения текущей СК | ||
| + | glPopMatrix(); | ||
| + | } | ||
| + | }; // end of 'ball_air' class | ||
| + | |||
| + | // Шар, летящий с сопротивлением воздуха | ||
| + | // Координаты получены из точного решения при линейной зависимости силы сопротивлении воздуха от скорости | ||
| + | class ball_air_2 : public sagl::object | ||
{ | { | ||
| − | + | private: | |
| − | + | double angle, v, m, n; | |
| − | + | public: | |
| − | + | // Конструктор | |
| − | + | ball_air_2( void ) : angle(Pi / 3), v(1), m(1), n(0.1) | |
| − | + | { | |
| − | + | P = sagl::vec(sagl::r0() + 5, 5, 0); | |
| − | + | V.X = 0; | |
| − | + | V.Y = sin(angle) * v; | |
| − | + | V.Z = cos(angle) * v; | |
| − | + | } | |
| − | + | ||
| − | + | // Конструктор | |
| − | + | ball_air_2( double angle1, double v1, double m1, double n1 ) : angle(angle1), v(v1), m(m1), n(n1) | |
| − | + | { | |
| − | + | P = sagl::vec(sagl::r0() + 5, 5, 0); | |
| − | + | V.X = 0; | |
| − | + | V.Y = sin(angle) * v; | |
| − | + | V.Z = cos(angle) * v; | |
| − | + | } | |
| − | + | ||
| − | + | // Отрисовка объекта | |
| − | + | void Render( sagl::anim &Ani ) | |
| − | + | { | |
| − | + | // Вектор ускорения свободного падения и вектор полного ускорения | |
| − | + | sagl::vec g = sagl::vec(0, -9.8, 0), a; | |
| − | + | // Размер комнаты | |
| − | + | double Size = 120; | |
| − | + | ||
| − | + | // Изменение вектора скорости | |
| − | + | V.Z = V.Z * exp(-n / m * Ani.DeltaTime); | |
| − | + | V.Y = (V.Y - g.Y * m / n) * exp(-n / m * Ani.DeltaTime) + g.Y * m / n; | |
| − | + | // Изменение вектора перемещения | |
| + | P += V * Ani.DeltaTime; | ||
| − | + | // Ограничения - стенки | |
| − | + | if (P.X > Size / 4) | |
| − | + | V.X = -fabs(V.X); | |
| − | + | if (P.X < -Size / 4) | |
| − | + | V.X = fabs(V.X); | |
| − | + | ||
| − | + | if (P.Y > Size / 4) | |
| − | + | V.Y = -fabs(V.Y); | |
| − | + | if (P.Y < -Size / 4) | |
| − | + | V.Y = fabs(V.Y); | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | if (P.Z > Size / 4) | |
| − | + | V.Z = -fabs(V.Z); | |
| − | + | if (P.Z < -Size / 4) | |
| − | + | V.Z = fabs(V.Z); | |
| − | |||
| − | + | // Запоминание состояния изменения текущей СК | |
| − | + | glPushMatrix(); | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | // Рисование стенок | ||
| + | glutWireCube(Size / 2); | ||
| + | // Задача перемещения мяча | ||
| + | glTranslated(P.X, P.Y, P.Z); | ||
| + | // Цвет мяча | ||
| + | glColor3d(0, 1, 1); | ||
| + | // Рисование мяча | ||
| + | glutSolidSphere(0.5, 30, 30); | ||
| + | |||
| + | // Восстановление последнего запоминания состояния изменения текущей СК | ||
| + | glPopMatrix(); | ||
| + | } | ||
| + | }; // end of 'ball_air_2' class | ||
| + | // Шар, летящий с сопротивлением воздуха | ||
| + | // Координаты получены методом Верле при линейной зависимости силы сопротивлении воздуха от скорости | ||
| + | class ball_air_3 : public sagl::object | ||
| + | { | ||
| + | private: | ||
| + | double angle, v, m, n; | ||
| + | public: | ||
| + | // Конструктор | ||
| + | ball_air_3( void ) : angle(Pi / 3), v(1), m(1), n(0.1) | ||
| + | { | ||
| + | P = sagl::vec(sagl::r0() + 5, 5, 0); | ||
| + | V.X = 0; | ||
| + | V.Y = sin(angle) * v; | ||
| + | V.Z = cos(angle) * v; | ||
| + | } | ||
| + | |||
| + | // Конструктор | ||
| + | ball_air_3( double angle1, double v1, double m1, double n1 ) : angle(angle1), v(v1), m(m1), n(n1) | ||
| + | { | ||
| + | P = sagl::vec(sagl::r0() + 5, 5, 0); | ||
| + | V.X = 0; | ||
| + | V.Y = sin(angle) * v; | ||
| + | V.Z = cos(angle) * v; | ||
| + | } | ||
| + | |||
| + | // Отрисовка объекта | ||
| + | void Render( sagl::anim &Ani ) | ||
| + | { | ||
| + | // Вектор ускорения свободного падения и вектор полного ускорения | ||
| + | sagl::vec g = sagl::vec(0, -9.8, 0), a; | ||
| + | // Размер комнаты | ||
| + | double Size = 120; | ||
| − | + | // Изменение вектора ускорения | |
| − | + | a = sagl::vec(0, g.Y - n / m * V.Y, -n / m * V.Z); | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | // Изменение вектора скорости | |
| + | V += a * Ani.DeltaTime; | ||
| + | // Изменение вектора перемещения | ||
| + | P += V * Ani.DeltaTime; | ||
| − | + | // Ограничения - стенки | |
| + | if (P.X > Size / 4) | ||
| + | V.X = -fabs(V.X); | ||
| + | if (P.X < -Size / 4) | ||
| + | V.X = fabs(V.X); | ||
| − | + | if (P.Y > Size / 4) | |
| − | + | V.Y = -fabs(V.Y); | |
| − | + | if (P.Y < -Size / 4) | |
| − | + | V.Y = fabs(V.Y); | |
| − | + | if (P.Z > Size / 4) | |
| − | / | + | V.Z = -fabs(V.Z); |
| + | if (P.Z < -Size / 4) | ||
| + | V.Z = fabs(V.Z); | ||
| − | + | // Запоминание состояния изменения текущей СК | |
| − | + | glPushMatrix(); | |
| − | |||
| − | |||
| − | /// | + | // Рисование стенок |
| − | + | glutWireCube(Size / 2); | |
| − | + | // Задача перемещения мяча | |
| − | + | glTranslated(P.X, P.Y, P.Z); | |
| − | + | // Цвет мяча | |
| − | + | glColor3d(1, 0.5, 0); | |
| − | + | // Рисование мяча | |
| − | + | glutSolidSphere(0.5, 30, 30); | |
| − | + | ||
| − | + | // Восстановление последнего запоминания состояния изменения текущей СК | |
| + | glPopMatrix(); | ||
| + | } | ||
| + | }; // end of 'ball_air_3' class | ||
| + | |||
| + | #endif /*__SAMPLE_H_ */ | ||
| + | |||
| + | // END OF 'SAMPLE.H' FILE | ||
| + | </syntaxhighlight> | ||
| + | </div> | ||
| + | [http://tm.spbstu.ru/File:T06BALL.7z Скачать архив] | ||
| + | <br> | ||
| + | |||
| + | '''[[Рубинова Раиса]]''' | ||
| − | + | '''Описание программы''': программа состоит из четырех независимых друг от друга частей: | |
| − | + | # Полет тела без сопротивления воздуха; | |
| − | + | # Полет тела при линейной зависимости силы сопротивления воздуха от скорости, при котором координаты тела рассчитываются точным методом; | |
| − | + | # Полет тела при линейной зависимости силы сопротивления воздуха от скорости, при котором координаты тела рассчитываются методом Верле; | |
| − | + | # Полет тела при квадратичной зависимости силы сопротивлении воздуха от скорости, при котором координаты тела рассчитываются методом Верле; | |
| − | + | ||
| − | + | Скачать можно [http://tm.spbstu.ru/File:Полет.rar тут]. | |
| − | + | ||
| − | + | <div class="mw-collapsible-content"> | |
| − | + | ||
| − | + | [[File:Обычный.png]] | |
| − | + | [[File:Точный.png]] | |
| − | + | [[File:Верле2.png]] | |
| − | + | [[File:Верле1.png]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | // | + | <syntaxhighlight lang="cpp" line start="1" enclose="div"> |
| + | // Первый случай | ||
#include <iostream> | #include <iostream> | ||
| Строка 1967: | Строка 2150: | ||
#include <fstream> | #include <fstream> | ||
| − | /// Программа, | + | /// Программа, анализирующая полет тела; |
using namespace std; | using namespace std; | ||
| − | double | + | double a,s,H,p1,p2,X,f; /// Создание переменных, необходимых для работы: |
| − | + | /// a - угол к горизонту, под которым летит тело, вводится пользователем; | |
| − | + | /// s - начальная скорость, с которой тело начинает лететь, вводится пользователем; | |
| − | + | /// H - координата тела по оси Oy; | |
| − | + | /// p1, p2 - промежуточные переменные, предназначенные для расчетов; | |
| − | + | /// X - координата тела по оси Oy; | |
| − | + | /// f - шаг по времени; | |
| − | |||
| − | |||
| − | |||
int main() | int main() | ||
{ | { | ||
| − | cout << "Enter speed and angle and step of time | + | cout << "Enter speed and angle and step of time" << endl; /// Обращение к пользователю, где требуется ввести скорость тела, угол к горизонту и шаг по времени; |
| − | cin >> | + | cin >> s >> a >> f; /// Считывание данных, введенных пользователем, в переменные; |
| − | double t= | + | double t=s*sin(a*3.14159/180.0)/9.8; /// Создание новой переменной t, хранящей значение времени полета тела вверх (вычисленное через уравнение скорости по оси Oy); |
| − | + | for (double i=f; i<(2*t+f); i+=f) /// Для вычисления координат тела в n-ом количестве точек мы создаем цикл, который повторяется то количество раз, сколько раз шаг по времени, введенным пользователем, вмещается во время полета всего тела; | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{ | { | ||
| − | + | p1=s*sin(a*3.14159/180)*i; /// Вычисление первой компоненты координаты тела по оси Oy, представляемй как произведение скорости по этой оси на время (выражено из уравнения равноускоренного прямолинейного движения); | |
| − | X | + | p2=4.9*i*i; /// Вычисление второй компоненты координаты тела по оси Oy, представляемой как произведение квадрата времени на половину укорения свободного падения (выражено из уравнения РУПД); |
| − | + | H=double(p1)-p2; /// Вычисление координаты тела по оси Oy; | |
| − | + | X=s*cos(a*3.14159/180)*i; /// Вычисление координаты тела по оси Ox как произведение скорости по оси Ox на время (выражено из уравнения равномерного движения); | |
| − | + | cerr << X << " "; /// Вывод на экран значения по оси Ox | |
| − | + | cerr << H << endl; /// и по оси Oy; | |
| − | out << X | + | } |
| − | + | ofstream out("zap.txt"); /// Так как результаты анализа не только выводятся на экран, но и записываются в файл, мы создаем переменную, соответствующую файлу "Res.txt", находящемуся в папке с программой, и открываем файл для записи; | |
| + | for (double i=0; i<(2*t+f); i+=f) /// Для вычисления координат тела в n-ом количестве точек мы создаем цикл, который повторяется то количество раз, сколько раз шаг по времени, введенным пользователем, вмещается во время полета всего тела; | ||
| + | { | ||
| + | p1=s*sin(a*3.14159/180)*i; /// Вычисление первой компоненты координаты тела по оси Oy, представляемй как произведение скорости по этой оси на время (выражено из уравнения равноускоренного прямолинейного движения); | ||
| + | p2=4.9*i*i; /// Вычисление второй компоненты координаты тела по оси Oy, представляемой как произведение квадрата времени на половину укорения свободного падения (выражено из уравнения РУПД); | ||
| + | H=double(p1)-p2; /// Вычисление координаты тела по оси Oy; | ||
| + | X=s*cos(a*3.14159/180)*i; /// Вычисление координаты тела по оси Ox как произведение скорости по оси Ox на время (выражено из уравнения равномерного движения); | ||
| + | out << X << " "; /// Запись в файл значения по оси Ox | ||
| + | out << H << endl; /// и по оси Oy; | ||
} | } | ||
out.close(); /// Закрываем файл, с которым работали в течение программы; | out.close(); /// Закрываем файл, с которым работали в течение программы; | ||
return 0; /// По умолчанию возвращаем функции int main значение 0, тем самым завершая программу; | return 0; /// По умолчанию возвращаем функции int main значение 0, тем самым завершая программу; | ||
| − | |||
| − | |||
} | } | ||
| − | // | + | // Второй случай |
#include <iostream> | #include <iostream> | ||
| Строка 2022: | Строка 2196: | ||
#include <fstream> | #include <fstream> | ||
| − | /// Программа, | + | /// Программа, позволяющая описать полет точки при помощи точного метода; |
using namespace std; | using namespace std; | ||
| − | double v,a,st,m | + | double v,a,st,m; /// Создание переменных, необходимых для работы: |
/// v - модуль скорости, который задает сам пользователь; | /// v - модуль скорости, который задает сам пользователь; | ||
/// a - угол относительно горизонта, под которым летит тело, задается пользователем; | /// a - угол относительно горизонта, под которым летит тело, задается пользователем; | ||
/// st - шаг по времени, через который расчитываются координаты точек, задается пользователем; | /// st - шаг по времени, через который расчитываются координаты точек, задается пользователем; | ||
/// m - масса тела, задается пользователем; | /// m - масса тела, задается пользователем; | ||
| − | |||
| − | |||
double *V,*X, *Y, *U; /// Создание массивов, хранящих значения типа double, в которых хранятся значения: | double *V,*X, *Y, *U; /// Создание массивов, хранящих значения типа double, в которых хранятся значения: | ||
/// V - массив, хранящий значения скорости по оси Ox; | /// V - массив, хранящий значения скорости по оси Ox; | ||
| Строка 2040: | Строка 2212: | ||
int main() | int main() | ||
{ | { | ||
| − | cout << "Enter speed and angle and step of time and weight" << endl; | + | cout << "Enter speed and angle and step of time and weight" << endl; /// Обращение к пользователю, где требуется ввести скорость тела, угол к горизонту, шаг по времени и массу тела; |
| − | cin >> v >> a >> st >> m; | + | cin >> v >> a >> st >> m; /// Считывание данных, введенных пользователей в переменные; |
| − | double t=(v/9.8)*sin(3.14159*a/180.0); | + | double t=(v/9.8)*sin(3.14159*a/180.0); /// Создание новой переменной t, хранящей значение времени всего полета тела, вычисленного, как два времени взлета (через уравнение скорости по оси Oy); |
| − | int n=2*t/st; | + | int n=2*t/st; /// Создание новой целочисленной переменной, которая равна времени полета тела (преобразование типов для переменной t) деленного на шаг, которая будет использоваться при создании массивов для размера; |
//int p=1/st; | //int p=1/st; | ||
V = new double [n+2]; /// Создание динамического массива V, предназначенного для хранения значений скорости по оси Ox, размером (n+2) (n показывает, сколько раз шаг по времени помещается во все время, то есть, сколько точек мы будем рассматривать, анализируя полет точки); | V = new double [n+2]; /// Создание динамического массива V, предназначенного для хранения значений скорости по оси Ox, размером (n+2) (n показывает, сколько раз шаг по времени помещается во все время, то есть, сколько точек мы будем рассматривать, анализируя полет точки); | ||
| Строка 2049: | Строка 2221: | ||
Y = new double [n+2]; /// Создание динамического массива X, предназначенного для хранения координаты тела по оси Oy и имеющего схожие характеристики с массивом V; | Y = new double [n+2]; /// Создание динамического массива X, предназначенного для хранения координаты тела по оси Oy и имеющего схожие характеристики с массивом V; | ||
U = new double [n+2]; /// Создание динамического массива U, предназначенного для хранения значений скорости тела по оси Oy и имеющего схожие характеристики с массивом V; | U = new double [n+2]; /// Создание динамического массива U, предназначенного для хранения значений скорости тела по оси Oy и имеющего схожие характеристики с массивом V; | ||
| − | V[0]=v*cos(3.14159*a/180.0); | + | V[0]=v*cos(3.14159*a/180.0); /// Вычисление значения скорости по оси Ox в начальный момент времени, как состовляющая модуля скорости, заданного пользователем; |
| − | X[0]=0; | + | X[0]=0; /// Задание координаты точки по оси Ox в начальный момент времени. Мы рассматриваем движение тела под углом к горизонту из начала координат, поэтому x=0; |
| − | + | U[0]=v*sin(3.14159*a/180.0); /// Вычисление значения скорости по оси Oy в начальный момент времени, как компонента модуля скорости, заданного пользователем, по вертикальной оси; | |
| − | + | Y[0]=0; /// Задание координаты точки по оси Oy в начальный момент времени. Мы рассматриваем движение тела под углом к горизонту из начала координат, поэтому y=0; | |
| − | U[0]=v*sin(3.14159*a/180.0); | ||
| − | Y[0]=0; | ||
| − | |||
| − | |||
| − | |||
ofstream out("Res.txt"); /// Так как результаты анализа не только выводятся на экран, но и записываются в файл, мы создаем переменную, соответствующую файлу "Res.txt", находящемуся в папке с программой, и открываем файл для записи; | ofstream out("Res.txt"); /// Так как результаты анализа не только выводятся на экран, но и записываются в файл, мы создаем переменную, соответствующую файлу "Res.txt", находящемуся в папке с программой, и открываем файл для записи; | ||
| − | + | for (int i=1; i<n; ++i) /// Для вычисления координат тела в пространстве в зависимости от времени мы создаем цикл, который позволяет, использая общую формулу нахождкения координат и компонент скорости, вычислять эти значения | |
| − | + | /// Цикл повторяется (n-1) раз, так как значения в начальный момент времени были найдены отдельно от цикла, и повторяется столько раз, сколько точек траектории мы рассматриваем; | |
| − | |||
| − | for (int i= | ||
| − | |||
{ | { | ||
| − | + | Y[i]=(m/0.001)*(U[0]+9.8*(m/0.001))*(1-exp(((0-0.001)/m)*i*st))-9.8*(m/0.001)*i*st; /// Вычисление координаты тела в момент времени (i*st) по оси Oy по формуле, выведенной через дифференциальное уравнение точки для вертикальной оси и находящей координату как функцию от времени и координаты тела в предыдущей рассматриваемой нами точке; | |
| − | + | X[i]=V[0]*(m/0.001)*(1-exp(((0-0.001)/m)*i*st)); /// Аналогично вычисляем координаты тела в момент времени (i*st) по оси Ox как функцию от времени и координате в предыдущей рассматриваемой точке; | |
| − | + | /// В приведенных выше формулах зачение 0.001 - это коэффициент сопротивления воздуха; | |
| − | + | /// Движение по горизонтальной оси рассматривается как равномерное прямолинейное движение; | |
| − | + | /// Движение по вертикальной оси рассматривается как равноускоренное прямолинейное движение; | |
| − | cerr << X[ | + | cerr << X[i] << " " << Y[i] << endl; /// Выведение рассчитанных значений на экран в виде строки, где первым идет координата по оси Ox, вторым - по оси Oy; |
| − | out << X[ | + | out << X[i] << " " << Y[i] << endl; /// Запись рассчитанных значений в файл "Res.txt" в виде строки, где первым идет координата по оси Ox, вторым - по оси Oy; |
| − | + | /// Таким образом, в результате работы программы мы получаем два столбика значений для координат по обеим осям, которые как записаны в файл, так и выведены на экран; | |
| − | |||
} | } | ||
| − | out.close(); | + | out.close(); /// Закрываем файл, с которым работали в течение программы; |
| − | return 0; | + | return 0; /// По умолчанию возвращаем функции int main значение 0, тем самым завершая программу; |
| + | |||
| + | |||
} | } | ||
| − | // | + | // Третий случай |
#include <iostream> | #include <iostream> | ||
| Строка 2086: | Строка 2251: | ||
#include <fstream> | #include <fstream> | ||
| − | /// Программа, анализирующая полет тела при помощи метода Верле; | + | /// Программа, анализирующая полет тела при помощи модифицированного метода Верле; |
using namespace std; | using namespace std; | ||
| − | double v,a,st,m,x,y; | + | double v,a,st,m,x,y; /// Создание переменных, необходимых для работы; |
| − | + | /// v - модуль скорости, который задает сам пользователь; | |
| − | + | /// a - угол относительно горизонта, под которым летит тело, задается пользователем; | |
| − | + | /// st - шаг по времени, через который расчитываются координаты точек, задается пользователем; | |
| − | + | /// m - масса тела, задается пользователем; | |
| − | + | /// x - координата тела по оси Ox в мнимый момент времени t=-1; | |
| − | + | /// y - координата тела по оси Oy в мнимый момент времени t=-1; | |
| − | double *V,*X, *Y, *U; | + | double *V,*X, *Y, *U; /// Создание массивов, хранящих значения типа double, в которых хранятся значения: |
| − | + | /// V - массив, хранящий значения скорости по оси Ox; | |
| − | + | /// X - массив, хранящий координаты точки по оси Ox; | |
| − | + | /// Y - массив, хранящий значения скорости по оси Oy; | |
| − | + | /// U - массив, хранящий координаты точки по оси Oy; | |
int main() | int main() | ||
{ | { | ||
| − | cout << "Enter speed and angle and step of time and weight" << endl; | + | cout << "Enter speed and angle and step of time and weight" << endl; /// Обращение к пользователю, где требуется ввести скорость тела, угол к горизонту, шаг по времени и массу тела; |
| − | cin >> v >> a >> st >> m; /// Считывание данных, введенных | + | cin >> v >> a >> st >> m; /// Считывание данных, введенных пользователей в переменные; |
double t=(v/9.8)*sin(3.14159*a/180.0); /// Создание новой переменной t, хранящей значение времени всего полета тела, вычисленного, как два времени взлета (через уравнение скорости по оси Oy); | double t=(v/9.8)*sin(3.14159*a/180.0); /// Создание новой переменной t, хранящей значение времени всего полета тела, вычисленного, как два времени взлета (через уравнение скорости по оси Oy); | ||
| − | int n=2*t/st; | + | int n=2*t/st; /// Создание новой целочисленной переменной, которая равна времени полета тела (преобразование типов для переменной t) деленного на шаг, которая будет использоваться при создании массивов для размера; |
//int p=1/st; | //int p=1/st; | ||
| − | V = new double [n+2]; | + | V = new double [n+2]; /// Создание динамического массива V, предназначенного для хранения значений скорости по оси Ox, размером (n+2) (n показывает, сколько раз шаг по времени помещается во все время, то есть, сколько точек мы будем рассматривать, анализируя полет точки); |
| − | X = new double [n+2]; | + | X = new double [n+2]; /// Создание динамического массива X, предназначенного для хранения координаты тела по оси Ox и имеющего схожие характеристики с массивом V; |
| − | Y = new double [n+2]; | + | Y = new double [n+2]; /// Создание динамического массива X, предназначенного для хранения координаты тела по оси Oy и имеющего схожие характеристики с массивом V; |
| − | U = new double [n+2]; | + | U = new double [n+2]; /// Создание динамического массива U, предназначенного для хранения значений скорости тела по оси Oy и имеющего схожие характеристики с массивом V; |
| − | V[0]=v*cos(3.14159*a/180.0); | + | V[0]=v*cos(3.14159*a/180.0); /// Вычисление значения скорости по оси Ox в начальный момент времени, как состовляющая модуля скорости, заданного пользователем; |
| − | X[0]=0; | + | X[0]=0; /// Задание координаты точки по оси Ox в начальный момент времени. Мы рассматриваем движение тела под углом к горизонту из начала координат, поэтому x=0; |
| − | x=X[0]-V[0]*st; | + | x=X[0]-V[0]*st; /// Суть данного метода заключается в том, что мы находим значение параметров тела по предыдущим двум состояниям, поэтому нам нужно вычислить мнимые координаты тела в -1 момент времени. Это расчет коордлинаты по оси Ox; |
| − | X[1]=2*X[0]-x-(0.01/m)*V[0] | + | X[1]=2*X[0]-x-(0.01/m)*V[0]*st*st; /// Вычисление координаты тела по оси Ox в момент времени t=1; |
U[0]=v*sin(3.14159*a/180.0); /// Вычисление значения скорости по оси Oy в начальный момент времени, как компонента модуля скорости, заданного пользователем, по вертикальной оси; | U[0]=v*sin(3.14159*a/180.0); /// Вычисление значения скорости по оси Oy в начальный момент времени, как компонента модуля скорости, заданного пользователем, по вертикальной оси; | ||
| − | Y[0]=0; | + | Y[0]=0; /// Задание координаты точки по оси Oy в начальный момент времени. Мы рассматриваем движение тела под углом к горизонту из начала координат, поэтому y=0; |
| − | y=Y[0]-U[0]*st; | + | y=Y[0]-U[0]*st; /// Суть данного метода заключается в том, что мы находим значение параметров тела по предыдущим двум состояниям, поэтому нам нужно вычислить мнимые координаты тела в -1 момент времени. Это расчет коордлинаты по оси Oу; |
| − | Y[1]=2*Y[0]-y-(0.01/m)*U[0] | + | Y[1]=2*Y[0]-y-(0.01/m)*U[0]*st*st; /// Вычисление координаты тела по оси Oу в момент времени t=1; |
cerr << X[1] << " " << Y[1] << endl; /// Вывод на экран значений координат по обеим осям в момент времени t=1; | cerr << X[1] << " " << Y[1] << endl; /// Вывод на экран значений координат по обеим осям в момент времени t=1; | ||
ofstream out("Res.txt"); /// Так как результаты анализа не только выводятся на экран, но и записываются в файл, мы создаем переменную, соответствующую файлу "Res.txt", находящемуся в папке с программой, и открываем файл для записи; | ofstream out("Res.txt"); /// Так как результаты анализа не только выводятся на экран, но и записываются в файл, мы создаем переменную, соответствующую файлу "Res.txt", находящемуся в папке с программой, и открываем файл для записи; | ||
| − | out << X[1] << " " << Y[1] << endl; | + | out << X[1] << " " << Y[1] << endl; /// Записываем в файл полученные значения координат тела в момент времени t=1; |
| − | int k=1; | + | int k=1; /// Создаем целочисленную переменную k=1 для работы в цикле; |
//cerr<<"N "<<n<<"\n"; | //cerr<<"N "<<n<<"\n"; | ||
| − | for (int i=0; i<n; ++i) | + | for (int i=0; i<n; ++i) /// Для вычисления координат тела в пространстве в зависимости от времени мы создаем цикл, который позволяет, использая общую формулу нахождкения координат и компонент скорости, вычислять эти значения |
| − | + | /// Цикл повторяется (n-1) раз, так как значения в начальный момент времени были найдены отдельно от цикла, и повторяется столько раз, сколько точек траектории мы рассматриваем; | |
{ | { | ||
| − | X[k+1]=2.0*X[k]-X[k-1]-(0.001/m) | + | X[k+1]=2.0*X[k]-X[k-1]-(0.001/m)*V[k]*st*st; /// Нахождение координаты тела по оси Ox в момент времени t, основываясь на известных параметрах за моменты времени t-1 и t-2; |
V[k]=(X[k+1]-X[k-1])/(2*st); /// Нахождение значения скорости тела по оси Ox в момент времени t-1, основываясь на рассчитанных выше координатах тела по оси Ox длямоментов времени t и t-2; | V[k]=(X[k+1]-X[k-1])/(2*st); /// Нахождение значения скорости тела по оси Ox в момент времени t-1, основываясь на рассчитанных выше координатах тела по оси Ox длямоментов времени t и t-2; | ||
| − | Y[k+1]=2.0*Y[k]-Y[k-1]-(9.8+(0.001/m) | + | Y[k+1]=2.0*Y[k]-Y[k-1]-(9.8+(0.001/m)*U[k])*st*st; /// Нахождение координаты тела по оси Oy в момент времени t, основываясь на известных параметрах за моменты времени t-1 и t-2; |
| − | U[k]=(Y[k+1]-Y[k-1])/(2*st); | + | U[k]=(Y[k+1]-Y[k-1])/(2*st); /// Нахождение значения скорости тела по оси Oy в момент времени t-1, основываясь на рассчитанных выше координатах тела по оси Ox длямоментов времени t и t-2; |
//cerr <<i<<" "<<k<<" "<< | //cerr <<i<<" "<<k<<" "<< | ||
cerr << X[k+1] << " " << Y[k+1] << endl; /// Выведение рассчитанных значений на экран в виде строки, где первым идет координата по оси Ox, вторым - по оси Oy; | cerr << X[k+1] << " " << Y[k+1] << endl; /// Выведение рассчитанных значений на экран в виде строки, где первым идет координата по оси Ox, вторым - по оси Oy; | ||
out << X[k+1] << " " << Y[k+1] << endl; /// Запись рассчитанных значений в файл "Res.txt" в виде строки, где первым идет координата по оси Ox, вторым - по оси Oy; | out << X[k+1] << " " << Y[k+1] << endl; /// Запись рассчитанных значений в файл "Res.txt" в виде строки, где первым идет координата по оси Ox, вторым - по оси Oy; | ||
k=k+1; /// Увеличиваем число k на единицу, чтобы в следующем шаге цикла рассчитать значения для следующего момента времени; | k=k+1; /// Увеличиваем число k на единицу, чтобы в следующем шаге цикла рассчитать значения для следующего момента времени; | ||
| − | + | /// Таким образом, в результате работы программы мы получаем два столбика значений для координат по обеим осям, которые как записаны в файл, так и выведены на экран; | |
} | } | ||
out.close(); /// Закрываем файл, с которым работали в течение программы; | out.close(); /// Закрываем файл, с которым работали в течение программы; | ||
| Строка 2143: | Строка 2308: | ||
} | } | ||
| − | + | // Четвертый случай | |
| − | |||
| + | #include <iostream> | ||
| + | #include <math.h> | ||
| + | #include <cstdlib> | ||
| + | #include <fstream> | ||
| − | + | /// Программа, анализирующая полет тела при помощи метода Верле; | |
| + | using namespace std; | ||
| + | double v,a,st,m,x,y; /// Создание переменных, необходимых для работы: | ||
| + | /// v - модуль скорости, который задает сам пользователь; | ||
| + | /// a - угол относительно горизонта, под которым летит тело, задается пользователем; | ||
| + | /// st - шаг по времени, через который расчитываются координаты точек, задается пользователем; | ||
| + | /// m - масса тела, задается пользователем; | ||
| + | /// x - координата тела по оси Ox в мнимый момент времени t=-1; | ||
| + | /// y - координата тела по оси Oy в мнимый момент времени t=-1; | ||
| + | double *V,*X, *Y, *U; /// Создание массивов, хранящих значения типа double, в которых хранятся значения: | ||
| + | /// V - массив, хранящий значения скорости по оси Ox; | ||
| + | /// X - массив, хранящий координаты точки по оси Ox; | ||
| + | /// Y - массив, хранящий значения скорости по оси Oy; | ||
| + | /// U - массив, хранящий координаты точки по оси Oy; | ||
| − | + | int main() | |
| − | + | { | |
| − | + | cout << "Enter speed and angle and step of time and weight" << endl; /// Обращение к пользователю, где требуется ввести скорость тела, угол к горизонту, шаг по времени и массу тела; | |
| − | + | cin >> v >> a >> st >> m; /// Считывание данных, введенных пользователем, в переменные; | |
| − | + | double t=(v/9.8)*sin(3.14159*a/180.0); /// Создание новой переменной t, хранящей значение времени всего полета тела, вычисленного, как два времени взлета (через уравнение скорости по оси Oy); | |
| − | + | int n=2*t/st; /// Создание новой целочисленной переменной, которая равна времени полета тела (преобразование типов для переменной t) деленного на шаг, которая будет использоваться при создании массивов для размера; | |
| − | + | //int p=1/st; | |
| − | + | V = new double [n+2]; /// Создание динамического массива V, предназначенного для хранения значений скорости по оси Ox, размером (n+2) (n показывает, сколько раз шаг по времени помещается во все время, то есть, сколько точек мы будем рассматривать, анализируя полет точки); | |
| − | + | X = new double [n+2]; /// Создание динамического массива X, предназначенного для хранения координаты тела по оси Ox и имеющего схожие характеристики с массивом V; | |
| − | + | Y = new double [n+2]; /// Создание динамического массива X, предназначенного для хранения координаты тела по оси Oy и имеющего схожие характеристики с массивом V; | |
| − | + | U = new double [n+2]; /// Создание динамического массива U, предназначенного для хранения значений скорости тела по оси Oy и имеющего схожие характеристики с массивом V; | |
| − | + | V[0]=v*cos(3.14159*a/180.0); /// Вычисление значения скорости по оси Ox в начальный момент времени, как состовляющая модуля скорости, заданного пользователем; | |
| − | < | + | X[0]=0; /// Задание координаты точки по оси Ox в начальный момент времени. Мы рассматриваем движение тела под углом к горизонту из начала координат, поэтому x=0; |
| − | " | + | x=X[0]-V[0]*st; /// Суть данного метода заключается в том, что мы находим значение параметров тела по предыдущим двум состояниям, поэтому нам нужно вычислить мнимые координаты тела в -1 момент времени. Это расчет коордлинаты по оси Ox; |
| − | < | + | X[1]=2*X[0]-x-(0.01/m)*V[0]*V[0]/cos(3.14159*a/180.0)*st*st; /// Вычисление координаты тела по оси Ox в момент времени t=1; |
| − | / | + | U[0]=v*sin(3.14159*a/180.0); /// Вычисление значения скорости по оси Oy в начальный момент времени, как компонента модуля скорости, заданного пользователем, по вертикальной оси; |
| − | + | Y[0]=0; /// Задание координаты точки по оси Oy в начальный момент времени. Мы рассматриваем движение тела под углом к горизонту из начала координат, поэтому y=0; | |
| − | + | y=Y[0]-U[0]*st; /// Суть данного метода заключается в том, что мы находим значение параметров тела по предыдущим двум состояниям, поэтому нам нужно вычислить мнимые координаты тела в -1 момент времени. Это расчет коордлинаты по оси Oу; | |
| − | + | Y[1]=2*Y[0]-y-(0.01/m)*U[0]*U[0]/sin(3.14159*a/180.0)*st*st; /// Вычисление координаты тела по оси Oу в момент времени t=1; | |
| − | + | cerr << X[1] << " " << Y[1] << endl; /// Вывод на экран значений координат по обеим осям в момент времени t=1; | |
| − | + | ofstream out("Res.txt"); /// Так как результаты анализа не только выводятся на экран, но и записываются в файл, мы создаем переменную, соответствующую файлу "Res.txt", находящемуся в папке с программой, и открываем файл для записи; | |
| − | + | out << X[1] << " " << Y[1] << endl; /// Записываем в файл полученные значения координат тела в момент времени t=1; | |
| − | /* | + | int k=1; /// Создаем целочисленную переменную k=1 для работы в цикле; |
| − | + | //cerr<<"N "<<n<<"\n"; | |
| − | + | for (int i=0; i<n; ++i) /// Для вычисления координат тела в пространстве в зависимости от времени мы создаем цикл, который позволяет, использая общую формулу нахождкения координат и компонент скорости, вычислять эти значения | |
| − | + | /// Цикл повторяется (n-1) раз, так как значения в начальный момент времени были найдены отдельно от цикла, и повторяется столько раз, сколько точек траектории мы рассматриваем; | |
| − | + | { | |
| − | + | X[k+1]=2.0*X[k]-X[k-1]-(0.001/m)*V[k]*V[k]*st*st; /// Нахождение координаты тела по оси Ox в момент времени t, основываясь на известных параметрах за моменты времени t-1 и t-2; | |
| − | + | V[k]=(X[k+1]-X[k-1])/(2*st); /// Нахождение значения скорости тела по оси Ox в момент времени t-1, основываясь на рассчитанных выше координатах тела по оси Ox длямоментов времени t и t-2; | |
| − | + | Y[k+1]=2.0*Y[k]-Y[k-1]-(9.8+(0.001/m)*U[k]*U[k])*st*st; /// Нахождение координаты тела по оси Oy в момент времени t, основываясь на известных параметрах за моменты времени t-1 и t-2; | |
| − | + | U[k]=(Y[k+1]-Y[k-1])/(2*st); /// Нахождение значения скорости тела по оси Oy в момент времени t-1, основываясь на рассчитанных выше координатах тела по оси Ox длямоментов времени t и t-2; | |
| + | //cerr <<i<<" "<<k<<" "<< | ||
| + | cerr << X[k+1] << " " << Y[k+1] << endl; /// Выведение рассчитанных значений на экран в виде строки, где первым идет координата по оси Ox, вторым - по оси Oy; | ||
| + | out << X[k+1] << " " << Y[k+1] << endl; /// Запись рассчитанных значений в файл "Res.txt" в виде строки, где первым идет координата по оси Ox, вторым - по оси Oy; | ||
| + | k=k+1; /// Увеличиваем число k на единицу, чтобы в следующем шаге цикла рассчитать значения для следующего момента времени; | ||
| + | /// Таким образом, в результате работы программы мы получаем два столбика значений для координат по обеим осям, которые как записаны в файл, так и выведены на экран; | ||
| + | } | ||
| + | out.close(); /// Закрываем файл, с которым работали в течение программы; | ||
| + | return 0; /// По умолчанию возвращаем функции int main значение 0, тем самым завершая программу; | ||
| + | } | ||
| − | + | </syntaxhighlight> | |
| − | + | </div> | |
| − | |||
| − | |||
| − | + | <div class="mw-collapsible mw-collapsed" style="width:100%" > | |
| − | + | '''[[Савельева Ольга]]''' | |
| − | |||
| − | |||
| − | + | '''Описание:''' Пользователя попросят ввести начальную скорость, угол бросания, тогда программа запишет в файл результаты следующих вычислений: | |
| − | + | # Координаты, рассчитанные по формуле, при движении без сопротивления воздуха; | |
| − | + | # Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости; | |
| − | + | # Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости. | |
| + | # Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости; | ||
| − | + | <div class="mw-collapsible-content"> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<syntaxhighlight lang="cpp" line start="1" enclose="div"> | <syntaxhighlight lang="cpp" line start="1" enclose="div"> | ||
| − | |||
| − | |||
| − | |||
| − | |||
#include <stdio.h> | #include <stdio.h> | ||
#include <stdlib.h> | #include <stdlib.h> | ||
| − | #include < | + | #include <cmath> |
| − | + | using namespace std; | |
| − | + | FILE *output; | |
| − | |||
| − | / | + | double e = 0.0000001; //точность |
| − | + | double g = 9.8; //ускорение свободного падения | |
| − | + | double dt = 0.00001; //шаг по времени | |
| − | + | double windageLinearCoefficient = 0.1; | |
| − | + | double windageSquareCoefficient = 0.00001; | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | / | + | struct Vector //вектор |
| − | |||
| − | |||
{ | { | ||
| − | + | double x, y; | |
| − | + | Vector():x(0), y(0) | |
| − | + | {} | |
| − | + | Vector(double x, double y):x(x), y(y) | |
| − | + | {} | |
| − | + | const Vector operator+(const Vector &v) const | |
| − | + | { | |
| + | return Vector(this -> x + v.x, this -> y + v.y); | ||
| + | } | ||
| + | const Vector operator-(const Vector &v) const | ||
| + | { | ||
| + | return Vector(this -> x - v.x, this -> y - v.y); | ||
| + | } | ||
| + | const Vector operator*(const double k) const | ||
| + | { | ||
| + | return Vector(this -> x * k, this -> y * k); | ||
| + | } | ||
| + | const Vector operator*(const int k) const | ||
| + | { | ||
| + | return Vector(this -> x * k, this -> y * k); | ||
| + | } | ||
| + | const Vector operator/(const double k) const | ||
| + | { | ||
| + | return Vector(this -> x / k, this -> y / k); | ||
| + | } | ||
| + | }; | ||
| − | + | const Vector operator*(const double a, const Vector &v) | |
| − | } | + | { |
| + | return Vector(v.x * a, v.y * a); | ||
| + | } | ||
| − | + | const Vector operator*(const int k, const Vector &v) | |
| − | |||
| − | |||
{ | { | ||
| − | + | return Vector(v.x * k, v.y * k); | |
| − | + | } | |
| − | |||
| − | |||
| − | + | double abs(const Vector &v) | |
| − | + | { | |
| − | + | return sqrt(v.x * v.x + v.y * v.y); | |
| + | } | ||
| − | + | void printCoordinate(const char *description, const Vector &v) //выводит координаты в более читаемом виде | |
| − | + | { | |
| + | fputs(description, output); | ||
| + | fputs(": ", output); | ||
| + | fprintf(output, "%lf", v.x); | ||
| + | fputs(", ", output); | ||
| + | fprintf(output, "%lf\n", v.y); | ||
| + | } | ||
| − | + | Vector getCoordinatesWithoutWindage(double velocity, double angle, double time = -1) | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{ | { | ||
| − | + | double fallTime = 2 * velocity * sin(angle) / g; //расчет времени падения | |
| − | + | if((time < 0) or (time > fallTime)) | |
| − | + | time = fallTime; | |
| − | + | double x = velocity * cos(angle) * time; // x = vx*t; | |
| − | + | double y = velocity * sin(angle) * time - g * time * time / 2; // y = vy*t-(g*t^2)/2; | |
| − | + | return Vector(x, y); | |
| − | + | } | |
| − | |||
| − | |||
| − | } | ||
| − | + | Vector getCoordinatesVerletLinear(double velocity, double angle, double time = -1) | |
| − | |||
{ | { | ||
| − | + | double nowTime = dt; | |
| − | + | Vector rsb(0, 0); | |
| − | + | if((time >= 0) and (dt / 2 - time > 0)) //если время расчета дается слишком малого промежутка | |
| − | + | return rsb; //вернитесь в начальную точку | |
| − | + | Vector v(velocity * cos(angle), velocity * sin(angle)); //проекции начальной скорости | |
| − | + | Vector r = v * dt; //вторая точка | |
| − | + | Vector a = -windageLinearCoefficient * v; //ускорение в начальной точке | |
| − | + | a.y -= g; | |
| − | + | v = v + a * dt; //скорость во второй точке | |
| − | + | a = -windageLinearCoefficient * v; //ускорение во второй точке | |
| − | + | a.y -= g; | |
| − | + | while((r.y > 0) or ((time > 0) and (nowTime <= time))) //пока точка выше 0 или не достигла заданного времени | |
| − | + | { | |
| − | + | Vector rn = 2 * r - rsb + a * dt * dt; // r(t+dt) = 2*r(t)-r(t-dt)+a(t)*dt^2; | |
| − | + | v = (rn - rsb) / (2 * dt); // v(t) = (r(t+dt)-r(t-dt))/(2*dt); | |
| − | + | rsb = r; //обновление r(t-dt) and r(t) | |
| − | + | r = rn; | |
| − | + | a = -windageLinearCoefficient * v; //обновление a(t) | |
| − | + | a.y -= g; | |
| − | + | nowTime += dt; //обновленное время | |
| − | + | } | |
| − | + | return r; | |
| − | |||
| − | |||
| − | |||
| − | |||
} | } | ||
| − | + | Vector calculateForTime(Vector &v, double time) | |
| − | |||
{ | { | ||
| − | + | Vector r; | |
| − | + | // x = vx/k*(1-e^(-k*t)); | |
| − | + | r.x = v.x / windageLinearCoefficient * (1 - exp(-windageLinearCoefficient * time)); | |
| + | // y = ((vy+g/k)*(1-e^(-k*t))-g*t)/k; | ||
| + | r.y = ((v.y + g / windageLinearCoefficient) * (1 - exp(-windageLinearCoefficient * time)) - g * time) / windageLinearCoefficient; | ||
| + | return r; | ||
} | } | ||
| − | + | Vector getCoordinatesAccurateLinear(double velocity, double angle, double time = -1) | |
| − | |||
| − | |||
{ | { | ||
| − | + | if(windageLinearCoefficient < e) //если коэффициент слишком близок к нулю | |
| − | + | return getCoordinatesWithoutWindage(velocity, angle, time); //вычисляй будто это 0 | |
| − | + | Vector r; | |
| − | + | Vector v(velocity * cos(angle), velocity * sin(angle)); //проекции начальной скорости | |
| − | + | if(time >= 0) //время данное | |
| − | // | + | { |
| − | + | r = calculateForTime(v, time); | |
| − | + | if(r.y >= 0) //если объект в воздухе или только приземлился | |
| − | + | return r; //затем верните координаты объекта | |
| − | + | else //еще | |
| − | } / | + | return getCoordinatesAccurateLinear(velocity, angle); //верните координаты приземления |
| − | + | } | |
| − | // | + | else |
| − | + | { | |
| − | + | double timer, timel, timem; | |
| − | + | timer = v.y / g; | |
| − | + | timel = 0; | |
| − | + | while(calculateForTime(v, timer).y > 0) //смотрим на некоторые значения времени, которые больше времени посадки | |
| − | + | timer *= 1.5; | |
| + | timem = timel + (timer - timel) / 2; | ||
| + | r = calculateForTime(v, timem); | ||
| + | while(abs(r.y) > e) //бинарный поиск времени посадки | ||
| + | { | ||
| + | if(r.y > 0) | ||
| + | timel = timem; | ||
| + | else | ||
| + | timer = timem; | ||
| + | timem = timel + (timer - timel) / 2; | ||
| + | r = calculateForTime(v, timem); | ||
| + | } | ||
| + | return r; | ||
| + | } | ||
| + | } | ||
| − | + | Vector getCoordinatesVerletSquare(double velocity, double angle, double time = -1) | |
| − | + | { | |
| − | + | double nowTime = dt; | |
| − | + | Vector rsb(0, 0); | |
| − | + | if((dt / 2 - time > 0)and(time >= 0)) //если время слишком малое для рсчета | |
| − | + | return rsb; //вернитесь в начальную точку | |
| + | Vector v(velocity * cos(angle), velocity * sin(angle)); //проекции начальной скорости | ||
| + | Vector r = v * dt; //вторая точка | ||
| + | Vector a = -abs(v) * v * windageSquareCoefficient; //ускорение в начальной точке | ||
| + | a.y -= g; | ||
| + | v = v + a * dt; //скорость во второй точке | ||
| + | a = -abs(v) * v * windageSquareCoefficient; //ускорение во второй точке | ||
| + | a.y -= g; | ||
| + | while((r.y > 0) or ((time > 0) and (nowTime <= time))) //когда точка выше нулевой отметки и не достигает заданного времени | ||
| + | { | ||
| + | Vector rn = 2 * r - rsb + a * dt * dt; // r(t+dt) = 2*r(t)-r(t-dt)+a(t)*dt^2; | ||
| + | v = (rn - rsb) / (2 * dt); // v(t) = (r(t+dt)-r(t-dt))/(2*dt); | ||
| + | rsb = r; //updating r(t-dt) and r(t) | ||
| + | r = rn; | ||
| + | a = -abs(v) * v * windageSquareCoefficient; //новое a(t) | ||
| + | a.y -= g; | ||
| + | nowTime += dt; //новое a(t) | ||
| + | } | ||
| + | return r; | ||
| + | } | ||
| − | + | void err(const char *s) //печатает сообщение об ошибке и завершает работу | |
| + | { | ||
| + | fputs(s, output); | ||
| + | exit(1); | ||
| + | } | ||
| − | + | int main(int argc, const char *argv[]) | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{ | { | ||
| − | + | double velocity, angle; | |
| − | + | bool needRead = true; | |
| − | + | if(argc==3) //если даны 2 аргумента | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{ | { | ||
| + | velocity = atof(argv[1]); //истолкование его как скорости и угла | ||
| + | angle = atof(argv[2]); | ||
| + | needRead = false; | ||
} | } | ||
| − | + | if(needRead) | |
| − | |||
| − | |||
{ | { | ||
| − | } // | + | puts("Enter initial velocity (m/s)"); |
| − | + | scanf("%lf", &velocity); | |
| − | + | } | |
| − | + | if(velocity < 0) //проверка, если скорость меньше 0 | |
| − | + | err("Initial velocity must be above 0"); | |
| − | + | if(needRead) | |
| − | + | { | |
| − | // | + | puts("Enter initial angle (0-180 degrees)"); |
| − | + | scanf("%lf", &angle); | |
| − | + | } | |
| − | + | if((angle < 0) or (angle > 180)) //проверка, что угол в нужном интервале | |
| + | err("Initial angle must be from 0 to 180"); | ||
| + | angle = angle / 180 * M_PI; // a = a/180*pi; преобразование угла из градусов в радианы | ||
| + | output = fopen("Coordinates.txt", "w"); //открытие результативного файла | ||
| + | //вычисление и печать 4 значений | ||
| + | printCoordinate("Without windage", getCoordinatesWithoutWindage(velocity, angle)); | ||
| + | printCoordinate("Verlet, linear dependence", getCoordinatesVerletLinear(velocity, angle)); | ||
| + | printCoordinate("Accurate, linear dependence", getCoordinatesAccurateLinear(velocity, angle)); | ||
| + | printCoordinate("Verlet, square dependence", getCoordinatesVerletSquare(velocity, angle)); | ||
| + | fclose(output); //закрытие файла | ||
| + | return 0; | ||
| + | } | ||
| + | </syntaxhighlight> | ||
| + | </div> | ||
| + | Скачать можно [http://tm.spbstu.ru/%D0%A4%D0%B0%D0%B9%D0%BB:%D0%9A%D0%BE%D0%BE%D1%80%D0%B4%D0%B8%D0%BD%D0%B0%D1%82%D1%8B.zip здесь] | ||
| + | |||
| + | <div class="mw-collapsible mw-collapsed" style="width:100%" > | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''[[Сенников Иван]]''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Суть программы:'''Программа позволяет отслеживать траекторию движения тела, брошенного под углом к горизонту, в каждом из четырех случаев/методов. | |
| − | |||
| − | + | '''Идея:''' Программа состоит из четырех методов: 1) движение тела без учета сопротивления воздуха; 2) движение тела с учетом сопротивления воздуха по первому методу Верле; 3) движение тела с учетом сопротивления воздуха по точному методу; 4) движение тела с учетом сопротивления воздуха по второму методу Верле. | |
| − | |||
| − | + | '''Инструкция:''' Результаты программы будут записаны в соответствующий файл (подробности смотри в самой программе). Пользователю будет предоставлена возможность ввести начальную скорость и угол, под которым и бросают тело. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Ссылка для скачиваний: [http://tm.spbstu.ru/Файл:Throws_v2.0.zip здесь]. | |
| − | + | </div> | |
| − | </ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <div class="mw-collapsible mw-collapsed" style="width:100%" > | |
| − | + | '''[[Степанянц Степан]]''' | |
| − | # | + | '''Описание программы''': программа записывает в четыре файла результаты вычисления: |
| − | # | + | # Координаты, рассчитанные по формуле, при движении без сопротивления воздуха; |
| + | # Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости; | ||
| + | # Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости; | ||
| + | # Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости. | ||
| − | // | + | Скачать можно [http://tm.spbstu.ru/%D0%A4%D0%B0%D0%B9%D0%BB:Mainpr.rar тут]. |
| − | namespace | + | |
| + | <div class="mw-collapsible-content"> | ||
| + | [[File:graph239.png]] | ||
| + | |||
| + | Для тела с массой 1,сопротивлением воздуха 0.05, угол бросания 30°, начальная скорость 40 м/с, ускорение свободного падения 9.8 м/c^2; | ||
| + | |||
| + | |||
| + | |||
| + | Файл "'''main.cpp'''" | ||
| + | <syntaxhighlight lang="cpp" line start="1" enclose="div"> | ||
| + | #include <iostream> | ||
| + | #include <locale.h> | ||
| + | #include <math.h> | ||
| + | #include <fstream> | ||
| + | #include<iomanip> | ||
| + | #include <cmath> | ||
| + | using namespace std; | ||
| + | main () | ||
{ | { | ||
| − | + | ofstream F; //a1-угол в градусах,dt-шаг,r-сопротивление воздуха | |
| − | + | int u0=50; | |
| − | + | double x,y,t,a,a1=30,dt=0.1,y0=0,x0=0,g=9.8,r=0.05,m=1,ux,uy,ypr,xpr,ysl,xsl,u,yt; //ux,uy - проэкции скорости на оси х и у. | |
| − | + | a=a1*M_PI/180; //Градусы в радианы | |
| − | + | t=0; | |
| − | + | ||
| − | + | //Движение без сопротивления воздуха | |
| − | + | F.open("C:\\1.txt",ios::out); | |
| − | + | while(y>=0) | |
| − | + | { | |
| − | + | x=x0+u0*cos(M_PI/6)*t; | |
| − | + | y=y0+u0*sin(M_PI/6)*t - 0.5 * g * t * t; //Расчитываем координаты в каждой точке через шаг | |
| − | + | F<<x<<" "<<y<<endl; | |
| − | + | t=t+dt; | |
| − | + | ||
| − | + | } | |
| − | + | ||
| − | + | F.close(); | |
| − | + | //Точное решение для линейной зависимости | |
| − | + | F.open("C:\\2.txt",ios::out); | |
| − | + | y=y0; | |
| − | + | x=x0; | |
| − | + | t=0; //Расчитываем координаты в каждой точке через шаг | |
| − | + | while(y>=0) | |
| − | + | { | |
| − | + | ux = u0 * cos(a); | |
| − | + | uy = u0 * sin(a); | |
| − | + | x = x0+ (m * ux / r)* (1 - exp(-1 * r * t / m)); //подстановка формул | |
| − | + | y = y0+(m/r)*((uy + g * m / r)*(1 - exp(-1 * r * t / m)) - g * t); | |
| − | + | t = t + dt; | |
| + | |||
| + | F << x << ' ' << y << endl; | ||
| + | |||
| + | |||
| + | |||
| + | } | ||
| + | F.close(); | ||
| + | //метод Верле 1 | ||
| + | ypr = y0 - u0*sin(a)*dt; | ||
| + | yt=ypr; | ||
| + | xpr = x0 - u0*cos(a)*dt; | ||
| + | x = x0; //Начальные условия | ||
| + | y = y0; | ||
| + | u = u0; | ||
| + | ux = u0 * cos(a); | ||
| + | uy = u0 * sin(a); | ||
| + | F.open("C:\\3.txt",ios::out); | ||
| + | |||
| + | while (y >= y0) | ||
{ | { | ||
| − | + | xsl = 2 * x - xpr - (r / m) * u * ux * (dt * dt); | |
| − | + | ux = ( xsl - xpr )/ (2 * dt); | |
| − | + | ysl = 2 * y - ypr - (g + (r / m) * u * uy) * (dt * dt); //xsl,ysl - координаты на шаге вперед. xpr,ypr- назад | |
| − | + | uy = (ysl - ypr)/ (2 * dt); | |
| − | + | u = sqrt(uy*uy + ux*ux ); | |
| − | + | F << x << ' ' << y << endl; | |
| + | |||
| + | xpr = x; | ||
| + | x = xsl; | ||
| + | ypr = y; | ||
| + | y = ysl; | ||
} | } | ||
| − | + | F.close(); | |
| − | + | //Метод Верле 2 | |
| − | + | ypr = y0 - u0*sin(a)*dt; | |
| − | + | yt=ypr; | |
| − | + | xpr = x0 - u0*cos(a)*dt; | |
| − | + | x = x0; //xsl,ysl - координаты на шаге вперед. xpr,ypr- назад | |
| − | + | y = y0; | |
| + | u = u0; | ||
| + | ux = u0 * cos(a); | ||
| + | uy = u0 * sin(a); | ||
| + | F.open("C:\\4.txt",ios::out); | ||
| + | |||
| + | while (y >= y0) | ||
{ | { | ||
| − | + | xsl = 2 * x - xpr - (r / m) * ux * (dt * dt); | |
| + | ux = ( xsl - xpr )/ (2 * dt); | ||
| + | ysl = 2 * y - ypr - (g + (r / m) * uy) * (dt * dt); | ||
| + | uy = (ysl - ypr)/ (2 * dt); | ||
| + | u = sqrt(uy*uy + ux*ux ); | ||
| + | F << x << ' ' << y << endl; | ||
| + | |||
| + | xpr = x; | ||
| + | x = xsl; | ||
| + | ypr = y; | ||
| + | y = ysl; | ||
} | } | ||
| − | + | F.close(); | |
| − | + | ||
| − | + | ||
| − | + | return 0; | |
| − | + | ||
| − | + | ||
| − | + | } | |
| − | + | ||
| − | + | </syntaxhighlight> | |
| − | + | </div> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | // | + | <div class="mw-collapsible mw-collapsed" style="width:100%" > |
| − | </ | + | '''[[Александр Сюрис]]''' |
| − | "''' | + | |
| + | '''Описание программы''': | ||
| + | Программа записывает в текстовый файл результаты вычисления координат по x и y с шагом в 0.1 секунду(возможно изменить) четырьмя различными способами: | ||
| + | #Координаты, рассчитанные по формуле, при движении без сопротивления воздуха | ||
| + | #Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости | ||
| + | #Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости | ||
| + | #Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости | ||
| + | Скачать можно [http://mech.spbstu.ru/File:%D0%9F%D0%BE%D0%BB%D0%B5%D1%82_%D1%82%D0%B5%D0%BB%D0%B0(%D0%90%D0%BB%D0%B5%D0%BA%D1%81%D0%B0%D0%BD%D0%B4%D1%80%D0%A1%D1%8E%D1%80%D0%B8%D1%81).zip тут]. | ||
| + | <div class="mw-collapsible-content"> | ||
| + | [[File:Снимок.PNG]] | ||
| + | Для тела с массой 1,сопротивлением воздуха 0.05, угол бросания 45°, начальная скорость 30 м/с, ускорение свободного падения 9.8 м/c^2; | ||
| + | Файл "'''main.cpp'''" | ||
<syntaxhighlight lang="cpp" line start="1" enclose="div"> | <syntaxhighlight lang="cpp" line start="1" enclose="div"> | ||
| − | + | #include <iostream> | |
| − | + | #include <fstream> | |
| − | + | #include <math.h> | |
| − | + | #include <cmath> | |
| − | + | using namespace std; | |
| − | + | int o; | |
| + | double v,a,m,k; | ||
| + | ofstream fout("file.txt");//создаем объект, сяванный с файлом file.txt | ||
| − | |||
| − | |||
| − | + | int rez_1(double v, double a) | |
| − | |||
{ | { | ||
| − | + | fout<<"---------------Первый режим-------------------------"<<endl; | |
| − | + | fout<<" T=0 x=0 y=0"; | |
| − | + | fout<<endl; | |
| − | + | double x=0,y=0,t=0.1, V0x, V0y, g=9.8,t1, T=0.1, Ty; | |
| − | + | V0x=v*cos(a/180*M_PI);//рассчет проекций начальных скоростей на оси x и y с переводом угла в радианы | |
| − | + | V0y=v*sin(a/180*M_PI); | |
| − | + | Ty=2*V0y/g;//время полета | |
| − | + | while (y>0 || x==0)//условие: пока тело не упадет на землю(те y=0, при этом не учитывая начало полета | |
| − | + | { | |
| − | + | x=x+V0x*t; //ф-лы для рассчета x и y в данный момент времени | |
| − | + | y=y+V0y*t-g*pow(t,2)/2; | |
| − | + | ||
| − | + | if (y<0) //если y<0 | |
| − | + | { | |
| − | + | t1=Ty-T; //рассчитываем время,которое осталось лететь телу до земли | |
| − | + | x=x+V0x*t1;//используя это время находим координату по х | |
| − | + | fout<<" T="<<Ty<<" x="<<x<<" y=0"<<endl;//ввод в текстовый файл | |
| − | + | break; | |
| − | + | } | |
| − | + | else | |
| − | + | { | |
| − | + | V0y=V0y-g*t;// иначе находим новую скорость по y (по x не меняется) | |
| − | + | fout<<" T="<<T<<" x="<<x<<" y="<<y<<endl; | |
| − | + | T=T+t;//увел время на шаг | |
| − | + | } | |
| − | + | } | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | } | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | int rez_2(double v, double a, double k, double m) | |
| − | + | { | |
| − | + | fout<<"---------------Второй режим работы-------------------------"<<endl; | |
| − | + | fout<<" T=0 x=0 y=0"; | |
| − | + | fout<<endl; | |
| − | // | + | double t=0.1, Vx=v*cos(a/180*M_PI), Vy=v*sin(a/180*M_PI),y,x,T=0.1,g=9.8; |
| − | + | x=(m*Vx/k)*(1-exp(-1*k*T/m)); //ф-лы для рассчета x и y в данный момент времени | |
| − | + | y =(m/k)*((Vy+g*m/k)*(1-exp(-1*k*T/m))-g*T); //точное решение при лин завсисимости | |
| − | + | while (y>0) | |
| − | + | { | |
| − | + | x=(m*Vx/k)*(1-exp(-1*k*T/m)); | |
| − | + | y =(m/k)*((Vy+g*m/k)*(1-exp(-1*k*T/m))-g*T); | |
| − | / | + | fout<<" T="<<T<<" x="<<x<<" y="<<y<<endl; |
| − | + | T=T+t; | |
| − | + | } | |
| − | + | ||
| − | + | ||
| − | + | } | |
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | int rez_3(double v, double a, double k, double m) | |
| − | + | { | |
| − | + | fout<<"---------------Третий режим работы-------------------------"<<endl; | |
| − | + | fout<<" T=0 x=0 y=0"; | |
| − | + | fout<<endl; | |
| − | + | double t=0.1, Vxn=v*cos(a/180*M_PI), Vyn=v*sin(a/180*M_PI), | |
| − | + | x3=0,x2=0,x1=x2-Vxn*t, y3=0, | |
| + | y2=0, y1=y2-Vyn*t, g=9.8, t1, T=0.1;//шаг, скорость по х в момент времени T, -\\- по y в момент времени Т | ||
| + | //координата по х в в момент времени T, -\\- в n-1 шаг, -\\- в n шаге, аналогично для y, | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | x3=2*x2-x1-k/m*Vxn*pow(t,2); //координаты в момент времени T | |
| − | + | y3=2*y2-y1-(g-+k/m*Vyn)*pow(t,2); | |
| − | + | Vxn=(x3-x1)/(2.0*t); //скорость в момент времени T | |
| − | + | Vyn=(y3-y1)/(2.0*t); | |
| + | x1=x2;// приравнивание к координате на n-1 шаге значение координаты в n шаге | ||
| + | y1=y2; | ||
| + | x2=x3;//-//- к координате в n шаге значение в момент времени T | ||
| + | y2=y3; | ||
| + | while (y2>0) | ||
| + | { | ||
| + | x3=2*x2-x1-k/m*Vxn*pow(t,2); | ||
| + | y3=2*y2-y1-(g+k/m*Vyn)*pow(t,2); | ||
| + | Vxn=(x3-x1)/(2.0*t); | ||
| + | Vyn=(y3-y1)/(2.0*t); | ||
| + | fout<<" T="<<T<<" x="<<x2<<" y="<<y2<<endl; | ||
| − | + | if (y3<0) | |
| − | + | { | |
| − | + | t1=sqrt(abs((-y1+2*y2)/(g+k/m*Vyn))); | |
| − | + | x3=2*x2-x1-k/m*Vxn*pow((t+t1),2); | |
| − | + | fout<<" T="<<T+t1<<" x="<<x3<<" y="<<0<<endl; | |
| − | + | } | |
| − | + | ||
| − | + | T=T+t; | |
| − | + | x1=x2; | |
| − | + | y1=y2; | |
| − | + | x2=x3; | |
| − | + | y2=y3; | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | } | |
| − | + | ||
| − | + | } | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | int rez_4(double v, double a, double k, double m) | |
| − | + | { | |
| − | + | fout<<"---------------Четвертый режим работы-------------------------"<<endl; | |
| − | + | fout<<" T=0 x=0 y=0"; | |
| − | + | fout<<endl; | |
| + | double t=0.1, Vxn=v*cos(a/180*M_PI), Vyn=v*sin(a/180*M_PI), | ||
| + | x3=0,x1=0, x2=x1+Vxn*t, y3=0, y1=0, | ||
| + | y2=y1+Vyn*t, g=9.8, t1, T=0.1, V=v;//шаг, скорость по х в момент времени T, -\\- по y в момент времени Т | ||
| + | //координата по х в в момент времени T, -\\- в n-1 шаг, -\\- в n шаге, аналогично для y, | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | x3=2.0*x2-x1-(k/m)*V*Vxn*pow(t,2); | |
| − | + | y3=2.0*y2-y1-(g+(k/m)*V*Vyn)*pow(t,2); | |
| − | + | Vxn=(x3-x1)/(2.0*t); | |
| − | + | Vyn=(y3-y1)/(2.0*t); | |
| + | V=sqrt(pow(Vxn,2)+pow(Vyn,2.0)); | ||
| + | x1=x2; | ||
| + | y1=y2; | ||
| + | x2=x3; | ||
| + | y2=y3; | ||
| + | while (y2>0) | ||
| + | { | ||
| + | x3=2.0*x2-x1-(k/m)*Vxn*V*pow(t,2); | ||
| + | y3=2.0*y2-y1-(g+(k/m)*Vyn*V)*pow(t,2); | ||
| + | Vxn=(x3-x1)/(2.0*t); | ||
| + | Vyn=(y3-y1)/(2.0*t); | ||
| + | V=sqrt(pow(Vxn,2)+pow(Vyn,2)); | ||
| + | fout<<" T="<<T<<" x="<<x2<<" y="<<y2<<endl; | ||
| − | + | if (y3<0) | |
| − | + | { | |
| + | t1=sqrt(abs((-y1+2.0*y2)/(g+(k/m)*Vyn*V))); | ||
| + | x3=2.0*x2-x1-(k/m)*Vxn*V*pow((t+t1),2); | ||
| + | fout<<" T="<<T+t1<<" x="<<x3<<" y="<<0<<endl; | ||
| + | } | ||
| + | |||
| + | |||
| + | T=T+t; | ||
| + | x1=x2; | ||
| + | y1=y2; | ||
| + | x2=x3; | ||
| + | y2=y3; | ||
| + | |||
| + | } | ||
| + | |||
| + | } | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | int main() | |
| − | |||
| − | |||
{ | { | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | setlocale(LC_ALL, "rus"); | |
| − | + | cout<<"Введите скорость тела и угол"<<endl; | |
| + | cin>>v>>a; | ||
| − | + | while (1>0){ | |
| − | + | cout<<"Выберите режим работы программы:"<<endl; | |
| − | + | cout<<"1 - Координаты, рассчитанные по формуле, при движении без сопротивления воздуха"<<endl; | |
| − | + | cout<<"2 - Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости"<<endl; | |
| + | cout<<"3- Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости"<<endl; | ||
| + | cout<<"4 - Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости"<<endl; | ||
| + | cout<<"5 - Выйти"; | ||
| + | cin>>o; | ||
| − | + | if (o==1) | |
| − | + | rez_1(v,a); | |
| − | + | if (o==2) | |
| − | + | { | |
| − | + | cout<<"Введите массу тела и коэф сопротивления воздуха:"<<endl; | |
| + | cin>>m>>k; | ||
| + | rez_2(v,a,k,m); | ||
| + | } | ||
| − | + | if (o==3) | |
| − | + | { | |
| − | + | cout<<"Введите массу тела и коэф сопротивления воздуха:"<<endl; | |
| − | + | cin>>m>>k; | |
| − | + | rez_3(v,a,k,m); | |
| − | + | } | |
| − | + | if (o==4) | |
| − | + | { | |
| − | + | cout<<"Введите массу тела и коэф сопротивления воздуха:"<<endl; | |
| + | cin>>m>>k; | ||
| + | rez_4(v,a,k,m); | ||
| + | } | ||
| + | if (o==5) | ||
| + | break; | ||
| − | + | } | |
| − | + | } | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | } | ||
| − | |||
| − | |||
</syntaxhighlight> | </syntaxhighlight> | ||
</div> | </div> | ||
| − | |||
| − | |||
| + | <div class="mw-collapsible mw-collapsed" style="width:100%" > | ||
| + | '''[[Тимошенко Валентина]]''' | ||
| + | '''Описание программы''': при запуске пользователь вводит шаг функции, угол, под которым бросают тело, массу тела, сопротивление воздуха и скорость. | ||
| + | Программа записывает в четыре файла результаты вычисления: | ||
| + | #Координаты, рассчитанные по формуле для движения без сопротивления воздуха; | ||
| + | #Координаты, рассчитанные по формуле для движения с учетом сопротивления воздуха; | ||
| + | #Координаты, полученные методом Верле при квадратичной зависимости силы сопротивления воздуха от скорости. | ||
| + | #Координаты, полученные методом Верле при линейной зависимости силы сопротивления воздуха от скорости; | ||
| − | + | Скачать можно [http://tm.spbstu.ru/Файл:motion.zip тут.] | |
| − | |||
| − | |||
| − | + | <div class="mw-collapsible-content"> | |
| − | |||
| − | |||
| − | |||
| + | '''Визуализированный результат работы программы''' | ||
| + | [[File:Grafics.png]] | ||
| − | + | Графики приведены для движения тела массой 1, со скоростью 50, под углом 45 градусов. Сопротивление воздуха принято равным 0.0001, шаг 0,1. | |
| − | + | <syntaxhighlight lang="cpp" line start="1" enclose="div"> | |
| − | |||
| − | + | #include <iostream> ///программа, подсчитывающая и записывающая в файл координаты движения тела для двух вариантов метода Верле | |
| − | + | #include <fstream> /// и для движений с учётом сопротивления и без его учёта | |
| + | #include <math.h> | ||
| + | #include<stdlib.h> | ||
| + | using namespace std; | ||
| − | + | int main() | |
| + | { | ||
| + | double a, step, Pi, g, Vo, m, r; | ||
| + | ///а - угол, под которым движется тело, step - шаг функции, Vo - начальная скорость тела, m - масса тела, r - величина сопротивления | ||
| + | double x, y, x_0, y_0, x0, y0, Vx, Vy; | ||
| + | ///переменные для движения точки без учёта сопротивления и с его учётом | ||
| + | ///х - изменяющаяся пошагово координата тела по оси Ох, у - изменяющаяся пошагово координата тела по оси Оу, | ||
| + | ///х0 - начальная координата тела по оси Ох, у0 - начальная координата тела по оси Оу | ||
| + | ///Vx - скорость тела по оси Ох, Vу - скорость тела по оси Оу | ||
| + | ///x_0 - изменяющаяся пошагово координата тела по оси Ох с учётом сопротивления, у_0 - изменяющаяся пошагово координата тела по оси Оу с учётом сопротивления | ||
| + | double Vy0, Vx0, x1, x2, x3, y1, y2, y3, Vxn, Vyn, Vn; | ||
| + | ///переменные для 1го варианта метода Верле | ||
| + | ///х1 - координата тела по оси Ох на (n-1) шаге, х2 - координата тела по оси Ох на (n) шаге, х3 - координата тела по оси Ох на (n+1) шаге | ||
| + | ///у1 - координата тела по оси Оу на (n-1) шаге, у2 - координата тела по оси Оу на (n) шаге, у3 - координата тела по оси Оу на (n+1) шаге | ||
| + | ///Vx0 - начальная скорость тела по оси Ох, Vy0 - начальная скорость тела по оси Оу | ||
| + | ///Vxn - скорость тела в данный момент времени по оси Ох, Vyn - скорость тела в данный момент времени по оси Оу | ||
| − | + | double Vxn2, Vyn2, x_1, x_2, x_3, y_1, y_2, y_3; | |
| − | + | ///переменные для 2го варианта метода Верле | |
| − | + | ///х_1 - координата тела по оси Ох на (n-1) шаге, х_2 - координата тела по оси Ох на (n) шаге, х_3 - координата тела по оси Ох на (n+1) шаге | |
| − | + | ///у_1 - координата тела по оси Оу на (n-1) шаге, у_2 - координата тела по оси Оу на (n) шаге, у_3 - координата тела по оси Оу на (n+1) шаге | |
| − | + | ///Vxn2 - скорость тела в данный момент времени по оси Ох, Vyn2 - скорость тела в данный момент времени по оси Оу | |
| − | + | g=10; ///значение ускорения свободного падения | |
| − | + | Pi=3.14159265; /// значение числа П, используем для перевода радиан в градусы | |
| − | |||
| − | |||
| − | + | do ///цикл, запрашивающий ввод пользователем значения шага функции | |
| + | { | ||
| + | cout << "Input the step, it must be less than 1" << endl; ///ввод с клавиатуры шага(то же самое, что дельта t), шаг должен быть маленьким (меньше 1) | ||
| + | cin >> step; ///вывод величины шага на экран | ||
| + | } | ||
| + | while (step>=1); ///выход из цикла не будет обеспечен, пока пользователь не введет число, меньшее 1 | ||
| − | </ | + | cout << '\n' << "Input the corner in degrees,the corner is in the range from 0 to 90 degrees" << endl; ///ввод с клавиатуры угла в радианах (угол от 0 до 90 градусов) |
| + | cin >> a; ///вывод значение угла на экран | ||
| + | a=(Pi*a)/180.0; | ||
| + | cout << '\n' << "Input the weight" << endl; ///ввод с клавиатуры значения массы | ||
| + | cin >> m; ///вывод величины массы на экран | ||
| − | </ | + | do ///цикл, запрашивающий ввод пользователем значения сопротивления воздуха |
| + | { | ||
| + | cout << '\n' << "Input the value of the resistance, it must be less than 1" << endl; ///ввод с клавиатуры величины сопротивления | ||
| + | cin >> r; ///вывод значения сопротивления на экран | ||
| + | } | ||
| + | while (r>=1); ///выход из цикла не будет обеспечен, пока пользователь не введет число, меньшее 1 | ||
| − | '' | + | cout << '\n' << "Input the speed" << endl; ///ввод с клавиатуры значения начальной скорости |
| + | cin >> Vo; ///вывод значения скорости на экран | ||
| − | + | ///для движения без учёта сопротивления | |
| + | x0=0; ///обнуление переменных | ||
| + | y0=0; | ||
| + | x=0; | ||
| + | y=0; | ||
| − | + | ///для движения с учётом сопротивления | |
| − | + | x_0=0; ///обнуление переменных | |
| − | + | y_0=0; | |
| − | |||
| − | + | ///для 1го варианта метода Верле | |
| − | + | Vx0=Vo*cos(a); ///расчет проекции начальной скорости по оси Ох | |
| + | Vy0=Vo*sin(a); ///расчет проекции начальной скорости по оси Оу | ||
| − | + | x2=0; ///обнуление переменных | |
| − | + | y2=0; | |
| + | x3=0; | ||
| + | y3=0; | ||
| − | + | y1=y2-Vy0*step; ///расчет начального значения координаты по оси Оу | |
| − | + | x1=x2-Vx0*step; ///расчет начального значения координаты по оси Ох | |
| − | |||
| − | |||
| − | |||
| − | + | ///для 2го варианта метода Верле | |
| − | |||
| + | x_2=0; ///обнуление переменных | ||
| + | y_2=0; | ||
| + | x_3=0; | ||
| + | y_3=0; | ||
| − | + | Vxn2=Vo*cos(a); ///расчет скорости тела на начальный момент времени по оси Ох | |
| + | Vyn2=Vo*sin(a); ///расчет скорости тела на начальный момент времени по оси Оу | ||
| + | y_1=y_2-Vo*sin(a)*step; ///расчет начального значения координаты на (п-1) шаге по оси Оу | ||
| + | x_1=-Vo*cos(a)*step; ///расчет начального значения координаты на (п-1) шаге по оси Ох | ||
| + | ofstream out("For method without resistance.txt"); | ||
| + | ///запись в файл значений координат по осям Ох и Оу для движения без сопротивления | ||
| − | + | for (int i=0; y>=0; ++i) ///цикл для подсчета координат при движении тела без учёта сопротивления | |
| + | { | ||
| + | x=Vo*step*i*cos(a); ///расчет координаты тела по оси х | ||
| + | y=Vo*sin(a)*i*step-(g*i*step*i*step)*0.5; ///расчет координаты тела по оси y | ||
| − | + | out << x << " " << y <<'\n'; ///вывод всех значений координат по оси х и по оси у при движении тела без учёта сопротивления | |
| + | } | ||
| + | out.close(); | ||
| − | + | ofstream out1 ("For method with resistance.txt"); | |
| + | ///запись в файл значений координат по осям Ох и Оу для движения с учётом сопротивления | ||
| − | + | for (int i=0; y_0>=0; ++i) ///цикл для подсчета координат при движении тела с учётом сопротивления | |
| − | + | { | |
| − | + | Vx=Vo*cos(a); ///расчет скорости тела по оси Ох | |
| − | + | Vy=Vo*sin(a); ///расчет скорости тела по оси Оу | |
| − | + | x_0=x0+(m/r)*Vx*(1.0 - exp((-r*i*step)/m)); ///расчет координаты тела по оси х | |
| − | + | y_0=y0+(m/r)*(Vy+g*(m/r))*(1.0 - exp((-r*i*step)/m))-g*i*step*(m/r); ///расчет координаты тела по оси y | |
| + | out1 << x_0 << " " << y_0 <<'\n'; ///вывод всех значений координат по оси х и по оси у при движении c учётом сопротивления | ||
| + | } | ||
| + | out1.close(); | ||
| − | + | ofstream out2 ("For method Verle 1.txt"); | |
| + | ///запись в файл значений координат по осям Ох и Оу для 1го варианта метода Верле | ||
| − | + | for (int i=0; y3>=0; ++i) ///цикл для подсчета координат и скорости по времени для 1го варианта метода Верле | |
| + | { | ||
| + | x3=2*x2-x1-(r/m)*Vn*Vxn*step*step; ///расчет координаты в данный момент времени по оси Ох | ||
| + | y3=2*y2-y1-(g+(r/m)*Vn*Vyn)*step*step; ///расчет координаты в данный момент времени по оси Оу | ||
| + | Vxn=(x3-x1)/(2.0*step); ///расчет скорости в данный момент времени по оси Оу | ||
| + | Vyn=(y3-y1)/(2.0*step); /// расчет скорости в данный момент времени по оси Ох | ||
| + | Vn=sqrt(Vxn*Vxn+Vyn*Vyn); ///расчет скорости тела по модулю | ||
| − | + | x1=x2; ///присваивание значению координаты х1 на (n-1) шаге значение координаты х2 на n шаге | |
| − | + | x2=x3; ///присваивание значению координаты х2 на (n) шаге значение координаты х3 на (n+1) шаге | |
| − | + | y1=y2; ///присваивание значению координаты у1 на (n-1) шаге значение координаты у2 на n шаге | |
| − | + | y2=y3; ///присваивание значению координаты у2 на (n) шаге значение координаты у3 на (n+1) шаге | |
| − | |||
| − | + | out2 << x3 << " " << y3 <<'\n'; ///вывод всех значений координат по оси Ох и по оси Оу на экран для 1го варианта метода Верле | |
| − | + | } | |
| + | out2.close(); | ||
| − | + | ofstream out3 ("For method Verle 2.txt"); | |
| − | + | ///запись в файл значений координат по осям Ох и Оу для 2го варианта метода Верле | |
| − | + | ||
| − | + | for (int i=0; y_3>=0; ++i) ///цикл для подсчета координат и скорости по времени для 2го варианта метода Верле | |
| − | + | { | |
| − | + | x_3=2*x_2-x_1-(r/m)*Vxn2*step*step; ///расчет координаты в данный момент времени по оси Ох | |
| − | + | y_3=2*y_2-y_1-(g+(r/m)*Vyn2)*step*step; ///расчет координаты в данный момент времени по оси Оу | |
| − | + | Vxn2=(x_3-x_1)/(2.0*step); ///расчет скорости в данный момент времени по оси Оу | |
| + | Vyn2=(y_3-y_1)/(2.0*step); ///расчет скорости в данный момент времени по оси Ох | ||
| − | + | x_1=x_2; ///присваивание значению координаты х_1 на (n-1) шаге значение координаты х_2 на n шаге | |
| + | x_2=x_3; ///присваивание значению координаты х_2 на (n) шаге значение координаты х_3 на (n+1) шаге | ||
| + | y_1=y_2; ///присваивание значению координаты у_1 на (n-1) шаге значение координаты у_2 на n шаге | ||
| + | y_2=y_3; ///присваивание значению координаты у_2 на (n-1) шаге значение координаты у_3 на (n+1) шаге | ||
| − | + | out3 << x_3 << " " << y_3 <<'\n'; ///вывод на экран всех значений координат по оси Ох и по оси Оу для 2го варианта метода Верле | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | } | |
| − | + | out3.close(); | |
| − | + | cout << '\n' << "All results are saved in files." << endl; ///вывод на экран сообщения о записи в файл всех результатов | |
| − | + | cout << '\n' << "The program is finished." << endl; ///вывод на экран сообщения о завершении работы программы | |
| − | + | return 0; | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
} | } | ||
| + | </syntaxhighlight> | ||
| + | </div> | ||
| − | + | <div class="mw-collapsible mw-collapsed" style="width:100%" > | |
| − | + | '''[[Уманский Александр]]''' | |
| − | |||
| − | |||
| − | + | '''Описание программы''': программа записывает в четыре файла результаты вычисления: | |
| − | + | # Координаты, рассчитанные по формуле, при движении без сопротивления воздуха; | |
| + | # Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости; | ||
| + | # Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости; | ||
| + | # Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости. | ||
| − | + | <div class="mw-collapsible-content"> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[File:Methods.rar|Скачать архив]] | |
| − | + | [[File:1.png]] | |
| − | |||
| − | |||
| − | |||
| − | + | <syntaxhighlight lang="cpp" line start="1" enclose="div"> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</syntaxhighlight> | </syntaxhighlight> | ||
</div> | </div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Текущая версия на 00:28, 16 июня 2016
Алгоритм: в специализированном классе хранятся данные о мяче, функции-члены, задающие различные типы движения тела, функции отрисовки движения мяча. Все расчёты ведутся в режиме реального времени с помощью дополнительных функций. Отрисовка движения мяча происходит с помощью графических средств библиотеки OpenGL.
Инструкция: при запуске программы пользователь видит полёт четырёх мячей в замкнутом пространстве с равными начальными условиями, но различными алгоритмами движения. При желании изменить тип движения мяча достаточно изменить лишь название функции движения конкретного объекта в функции Display.
Ссылка для скачивания: [1]
Краткое описание алгоритма: в классе находятся координаты по формулам и записываются в файл.
Инструкция : Пользователь должен ввести начальную скорость, угол и шаг, с которым будут рассчитываться координаты. В файл координаты записываются в таком порядке: 1, 2 столбики - Координаты, рассчитанные по формуле, при движении без сопротивления воздуха; 3, 4 - Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости; 5,6 - Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости; 7,8 - Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости.
Скачать можно тут.
Визуализированный результат работы программы
Для тела с массой 1 кг,сопротивлением воздуха 0.001, угол бросания 60°, начальная скорость 50 м/с, ускорение свободного падения 9.8 м/c^2, шаг 0.00001;
- "MyFile.txt" using 1 : 2 - координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
- "MyFile.txt" using 3 : 4 - Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости;
- "MyFile.txt" using 5 : 6 - Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости;
- "MyFile.txt" using 7 : 8 - Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости.
1 #include <iostream>
2 #include <fstream>
3 #include "math.h"
4 #include <iomanip>
5 using namespace std;
6 class func
7 {
8
9 private:
10 double speed0, angle0, step ;
11 double time;
12
13 public:
14 double const g=9.8, n=0.001, m=1;///постоянная g, n-коэфициент сопротивления воздухаб m-масса
15 double t, amount;
16 int amountint;
17 func ( double _speed0, double _angle0, double _step ):speed0(_speed0), angle0(_angle0), step(_step)
18 {
19 angle0=(3.14159*angle0) / 180 ; ///перевод угла в радианы
20
21 time = ( 2*speed0*sin(angle0) ) / g;///подсчет полного времени полета
22 amount = (time/step) + 1;///количество точек для траектории
23 amountint = static_cast<int> (amount) ;
24
25
26 }
27
28
29
30 void SaveFile(char filename[])
31 {
32 double x0=0, y0=0;
33 double xv1=0, x1=0, y1=0, Vx1=speed0*cos(angle0),Vy1=speed0*sin(angle0), V1=speed0, yv1=0;
34 double xm1=x0-speed0*cos(angle0)*step, ym1=y0-speed0*sin(angle0)*step;
35 double xv2=0, x2=0, y2=0, Vx2=speed0*cos(angle0),Vy2=speed0*sin(angle0), V2=speed0, yv2=0;
36 double xm2=x0-speed0*cos(angle0)*step, ym2=y0-speed0*sin(angle0)*step;
37 double x3,y3;
38 std::ofstream fout(filename);
39 for (int i=0; (y0+(speed0*sin(angle0)*i*step - (g*i*i*step*step*0.5)))>=0; i++)
40 {
41 ///Верле линейная зависимость
42 x2=2*xv2-xm2-(n/m)*step*step*Vx2;
43 y2=2*yv2-ym2-(g+(n/m)*Vy2)*step*step;
44 Vx2=(x2-xm2) / (2.0*step);
45 Vy2=(y2-ym2) / (2.0*step);
46 xm2=xv2;
47 xv2=x2;
48 ym2=yv2;
49 yv2=y2;
50
51 ///точное решение
52 x3=x0+speed0*cos(angle0)*(m/n)*(1.0-exp(-(n/m)*i*step));
53 y3=y0+(m/n)*(speed0*sin(angle0) + g*(m/n))*(1.0-exp(-(n/m)*i*step))-g*(m/n)*i*step;
54
55 ///метод Верле, квадратичная зависимость
56 x1=2*xv1-xm1-(n/m)*step*step* Vx1 * V1;
57 y1=2*yv1-ym1-(g+(n/m)*V1*Vy1)*step*step;
58 Vx1=(x1-xm1) / (2.0*step);
59 Vy1=(y1-ym1) / (2.0*step);
60 V1=sqrt(Vx1*Vx1+Vy1*Vy1);
61 xm1=xv1;
62 xv1=x1;///запоминание предыдущего шага
63 ym1=yv1;
64 yv1=y1;
65
66
67
68 fout<< setw(20) << (x0+(speed0*cos(angle0)*step*i)) << setw(20) << (y0+(speed0*sin(angle0)*i*step - (g*i*i*step*step*0.5)))<<setw(20) << x1 << setw(20) << y1 <<setw(20) << x2 << setw(20)<<y2<<setw(20) << x3 << setw(20) << y3<<" \n";
69
70 }
71 fout.close();
72 }
73
74 };
75
76
77 int main()
78 {
79 double V0, angle, step;
80 cout << " enter V0 = ";///введите начальную скорость
81 cin >> V0;
82 cout << " enter an angle , 0 < angle <= 90, angle = " ;///введите угол в диапозоне от 0 до 90 градусов
83 cin >> angle;
84 cout << "\n enter step ";///введите шаг, с которым будут рассчитываться координаты
85 cin >> step; cout << endl;
86 func f1(V0,angle,step);///создание траектории
87 f1.SaveFile("Myfile.txt");///запись в файл
88
89
90 return 0;
91 }
Описание программы : программа записывает в четыре файла результаты вычисления:
Координаты, рассчитанные по формуле, при движении без сопротивления воздуха; Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости; Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости; Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости.
Посмотреть программу можно здесь
Описание программы: пользователь вводит начальную скорость полета, угол бросания и шаг, с которым будут рассчитаны точки.
Программа записывает в один файл результаты вычисления:
- Координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
- Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости;
- Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости.
- Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости;
Скачать можно тут.
Визуализированный результат работы программы
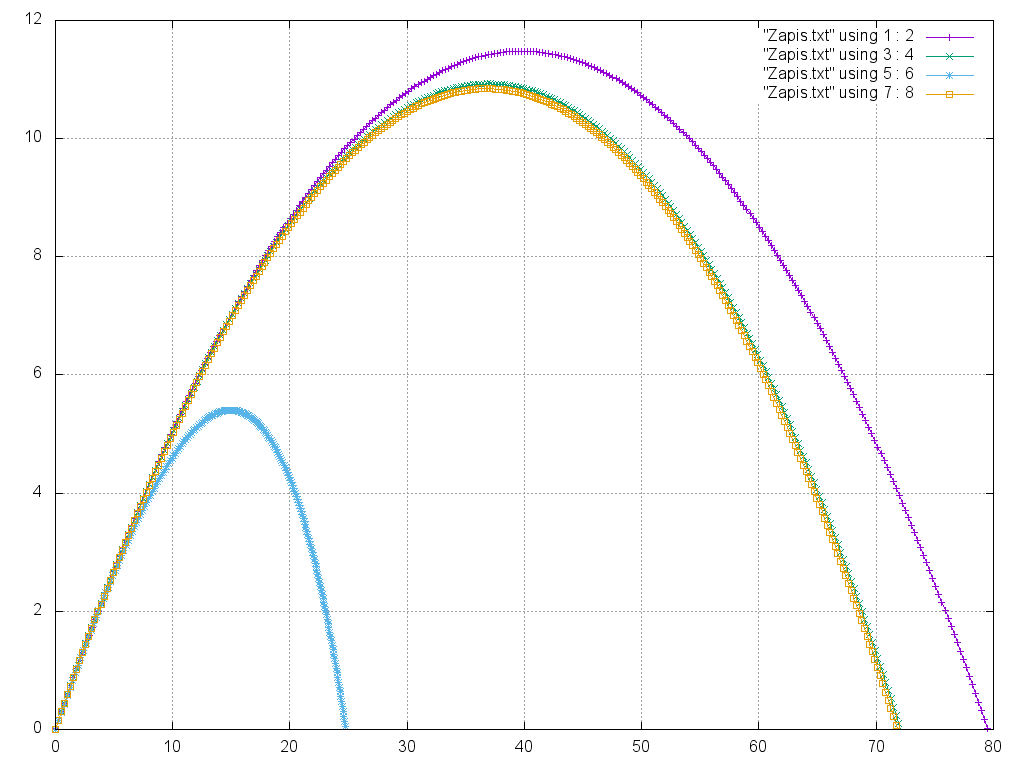
Для тела с массой 1 кг,сопротивлением воздуха 0.05, угол бросания 30°, начальная скорость 30 м/с, ускорение свободного падения 9.8 м/c^2, шаг 0.01;
- "Zapis.txt" using 1 : 2 - координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
- "Zapis.txt" using 3 : 4 - координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости;
- "Zapis.txt" using 5 : 6 - координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости;
- "Zapis.txt" using 7 : 8 - координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости.
1 #include <iostream>
2 #include <locale.h>
3 #include <math.h>
4 #include <fstream>
5 #include<iomanip>
6 #include <cmath>
7
8 using namespace std;
9
10 class fly ///создаем класс полета тела
11 {
12
13 private: ///объявляем тип переменных в привате
14 double Vo, Agrad, Brad, time, step, amountdouble; ///Vo-начальная скорость тела; Agrad-угол, под которым летит тело, в градусах;
15 ///Brad-угол, под которым летит тело, в радианах; time-время полета тела; step-шаг;
16 ///amountdouble-количество точек (типа double)
17
18 public: ///объявляем переменные в паблике
19 int amount; ///amoun-количество точек (типа int)
20
21 fly (double _step, double _Agrad, double _Vo):step(_step),Agrad(_Agrad),Vo(_Vo) ///создаем конструктор функции с объявлением переменных
22 {
23
24 double g=9.8; ///объявляем тип и значение переменной g(ускорение свободного падения)
25 Brad=3.14159*Agrad/180.0; ///переводим значение угла из градусов в радианы
26
27 time=2*Vo*sin(Brad)/g; ///рассчитываем время полета тела
28 amountdouble=(round(time/step)+1); ///подсчитываем количество точек с заданым шагом
29 amount=static_cast<int>(amountdouble); ///преобразуем количество из типа double к типу int
30
31 }
32 void zapis (char Zapis[]) ///создаем функцию записи
33 {
34 double g=9.8, m=1, n=0.05; ///объявляем тип и значения переменных g (ускорение свободного падения), m (масса тела), n(коэффициэнт сопротивления)
35 double Xb, Yb; ///объявляем тип переменных для полёта тела без сопротивления ветра Xb(координата тела по Х), Yb(координата тела по У)
36 double V=Vo, Vxv=Vo*cos(Brad), Vyv=Vo*sin(Brad), Xo=0, Yo=0, Xv=0, Yv=0, Y_1=Yo-Vo*sin(Brad)*step, X_1=Xo-Vo*cos(Brad)*step, Y=0, X=0;
37 ///объявляем тип переменных для метода ВерлеI V (скорость тела по модулю), Vxv (составляющая скорости по Х),
38 ///Vyv (составляющая скорости по У), Xo (начальное положение тела на оси Х), Yo (начальное положение тела на оси У),
39 ///Xv (координата тела на оси Х), Yv (координата тела на оси У), Y_1 (координата тела на (n-1)ом шаге на оси У),
40 ///X_1 (координата тела на (n-1)ом шаге на оси Х), Y (координата тела на n-ом шаге на оси У),
41 ///X (координата тела на n-ом шаге на оси Х);
42 double Vxv2=Vo*cos(Brad), Vyv2=Vo*sin(Brad), Xo2=0, Yo2=0, Xv2=0, Yv2=0, Y_12=Yo2-Vo*sin(Brad)*step, X_12=Xo-Vo*cos(Brad)*step, Y2=0, X2=0;
43 ///объявляем тип переменных для метода ВерлеII V (скорость тела по модулю), Vxv (составляющая скорости по Х),
44 ///Vyv (составляющая скорости по У), Xo (начальное положение тела на оси Х), Yo (начальное положение тела на оси У),
45 ///Xv (координата тела на оси Х), Yv (координата тела на оси У), Y_1 (координата тела на (n-1)ом шаге на оси У),
46 ///X_1 (координата тела на (n-1)ом шаге на оси Х), Y (координата тела на n-ом шаге на оси У),
47 ///X (координата тела на n-ом шаге на оси Х);
48 double Yt=0, Xt=0, Yot=0, Xot=0, Voxt=Vo*cos(Brad), Voyt=Vo*sin(Brad);
49
50 ofstream outfile("Zapis.txt"); ///запись элементов функции в фаил "Zapis.txt"
51 outfile<<setw(20)<<"Xb"<<setw(20)<<"Yb"<<setw(20)<<"Xt"<<setw(20)<<"Yt"<<setw(20)<<"Xv"<<setw(20)<<"Yv"<<setw(20)<<"Xv2"<<setw(20)<<"Yv2"<<" \n"; ///вывод на экран по столбцам
52 ///X (координата тела на оси Х без ветра),
53 ///Y (координата тела на оси У без ветра),
54 ///Xv (координата тела на оси Х с ветром для метода Верле),
55 ///Yv (координата тела на оси У с ветром для метода Верле)
56 ///setw() размер столбиков
57
58 for (int l=0; Yb>=0; ++l) ///создаем цикл от 0 до тех пор пока У больше нуля
59 {
60 outfile<<setw(20)<<Xb<<setw(20)<<Yb<<setw(20)<<Xt<<setw(20)<<Yt<<setw(20)<<Xv<<setw(20)<<Yv<<setw(20)<<Xv2<<setw(20)<<Yv2<<" \n";
61 ///вывод на экран по столбцам Xv, Yv;
62
63 ///полёт без ветра
64 Xb=Vo*cos(Brad)*l*step;
65 Yb=Vo*sin(Brad)*l*step-(9.8*l*step*l*step*0.5);
66
67 ///точный метод
68 Xt=Xot+(m/n)*Voxt*(1.0 - exp((-n*l*step)/m));
69 Yt=Yot+(m/n)*(Voyt+g*(m/n))*(1.0 - exp((-n*l*step)/m))-g*l*step*(m/n);
70
71 ///метод Верле I
72 Xv=2*X-X_1-(n/m)*V*Vxv*step*step; ///расчитываем координату Х в момент времени t для метода Верле
73 Yv=2*Y-Y_1-(g+(n/m)*V*Vyv)*step*step; ///расчитываем координату У в момент времени t для метода Верле
74 Vxv=(Xv-X_1)/(2.0*step); ///расчитываем скорость тела по оси Х в момент времени t для метода Верле
75 Vyv=(Yv-Y_1)/(2.0*step); ///расчитываем скорость тела по оси У в момент времени t для метода Верле
76 V=sqrt(Vxv*Vxv+Vyv*Vyv); ///рассчитываем скорость тела по модулю
77 X_1=X; ///присваиваем значению координаты Х на (n-1)ом шаге значение координаты Х на n-ом шаге
78 X=Xv; ///присваиваем значению координаты Х на n-ом шаге значение координаты Х
79 Y_1=Y; ///присваиваем значению координаты У на (n-1)ом шаге значение координаты У на n-ом шаге
80 Y=Yv; ///присваиваем значению координаты У на n-ом шаге значение координаты У
81
82 ///метод Верле II
83 Xv2=2*X2-X_12-(n/m)*Vxv2*step*step; ///расчитываем координату Х в момент времени t для метода Верле
84 Yv2=2*Y2-Y_12-(g+(n/m)*Vyv2)*step*step; ///расчитываем координату У в момент времени t для метода Верле
85 Vxv2=(Xv2-X_12)/(2.0*step); ///расчитываем скорость тела по оси Х в момент времени t для метода Верле
86 Vyv2=(Yv2-Y_12)/(2.0*step); ///расчитываем скорость тела по оси У в момент времени t для метода Верле
87 X_12=X2; ///присваиваем значению координаты Х на (n-1)ом шаге значение координаты Х на n-ом шаге
88 X2=Xv2; ///присваиваем значению координаты Х на n-ом шаге значение координаты Х
89 Y_12=Y2; ///присваиваем значению координаты У на (n-1)ом шаге значение координаты У на n-ом шаге
90 Y2=Yv2; ///присваиваем значению координаты У на n-ом шаге значение координаты У
91
92 }
93
94 outfile.close();
95
96 }
97
98 };
99
100 int main()
101 {
102
103 setlocale(LC_ALL,"RUS"); ///функция, позволяющая с++ распознавать русский язык
104
105 double Vo, Agrad, Brad, time, step; ///объявляем тип переменных Vo (начальная скорость тела), Agrad (угол, под которым летит тело, в градусах);
106 ///Brad (угол, под которым летит тело, в радианах); time (время полета тела); step (шаг)
107 cout<<"Задайте начальную скорость тела в м/с: Vo="; ///на экран выводится сообщение с просьюой задать начальную скорость тела
108 cin>>Vo; ///пользователь вводит начальную скорость тела
109 cout<<'\n'<<"Задайте в градусах угол, под которым брошено тело (угол должен принимать значения от 0 до 90): a=";
110 ///на экран выводится сообщение с просьбой задать угол, под которым летит тело, в градусах
111 cin>>Agrad; ///пользователь вводит угол, под которым летит тело
112 cout<<'\n'<<"Задайте шаг (шаг должен быть очень маленьким): шаг="; ///на экран выводится сообщение с просьбой ввести шаг
113 cin>>step; ///пользователь вводит шаг
114
115 fly X(step,Agrad,Vo); ///объявление коструктора, создание функции Х, зависящей от step,Agrad,Vo
116 X.zapis("координаты.txt"); ///запись элементов функции в файл
117
118 return 0; ///конец программы
119
120 }
Описание программы: пользователь вводит начальную скорость полета, угол падения и шаг, с которым будут рассчитаны точки.
Программа записывает в один файл результаты вычисления:
- Координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
- Координаты, полученные при численном интегрировании - метод Эйлера;
- Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости.
- Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости;
Скачать можно тут.
Визуализированный результат работы программы
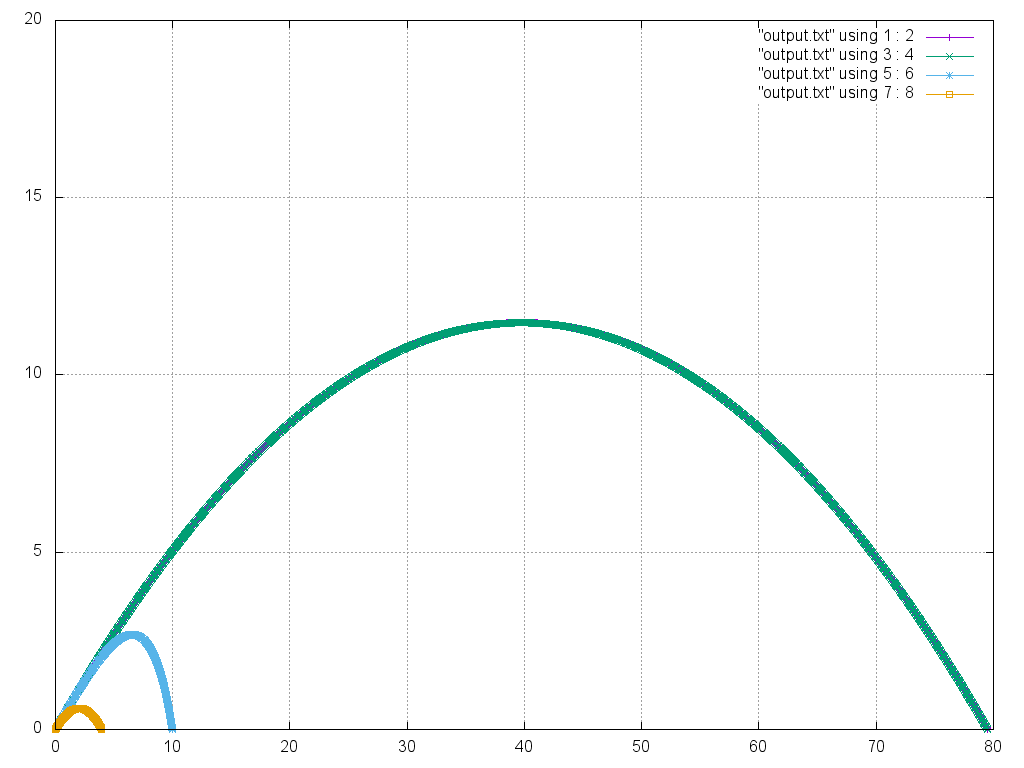
Для тела с массой 0.5 кг,сопротивлением воздуха 0.1, угол бросания 30°, начальная скорость 30 м/с, ускорение свободного падения 9.8 м/c^2, шаг 0.001;
- "output.txt" using 1 : 2 - координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
- "output.txt" using 3 : 4 - координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости (численное интегрирование - метод Эйлера);
- "output.txt" using 5 : 6 - координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости;
- "output.txt" using 7 : 8 - координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости.
1 #include <iostream>
2 #include <fstream>
3 #include <iomanip>
4 #include <time.h>
5 #include <conio.h>
6 #include <stdlib.h>
7 #include <math.h>
8 #include <cstring>
9 using namespace std;
10
11 class pad ///создаем класс
12 {
13 private: ///в закрытом доступе
14 double *X, *Y, *E, *G, *Z, *S, *V, *U; ///координаты по х и у; *E, *G : численное интегрирование метод Эйлера, *Z, *S- метод верле, *V, *U- точный метод
15 double a, g , pi;///ускорение, коэфф свободного падения, значение числа пи
16 int Size; ///размер массива- сколько точек считать в первом способе
17 double v, shag, b, vx, vy;///скорость, шаг по времени, угол в градусах скорость по х, скорость по у
18
19 void SetX() ///создаем функцию для вычисления значенй по х для простого падения и по эйлеру
20 {
21 g = 9.8;///коэфф свободного падения
22 float t = 0; ///время
23 X = new double [Size];///создаем массив для координат по х для простого падения
24 E = new double [Size];///создаем массив для координат по х для интегрирования по эйлеру
25 X[0] = 0; ///задаем значение по х в нуле
26 E[0] = 0 ; ///задаем значение по х в нуле по эйлеру
27 for (int i = 1; i < Size; i++) ///задаем цикл от 1 (для нуля мы задали), чтобы считать координаты
28 {
29 t += shag; ///каждый раз прибавляем по времени шаг
30 X[i] = v * cos(a) * t; ///координаты по х для простого падения
31 E[i] = E[i-1] + v * cos(a) * shag; ///х из интегрирования по эйлеру
32 }
33 }
34
35 void SetY()///создаем функцию для вычисления значенй по у для простого падения и по эйлеру
36 {
37 g = 9.8; ///коэфф свободного падения
38 double Vy; /// переменная для значение скорости по у для метода эйлера
39 float t = 0; ///время
40 Y = new double [Size];///создаем массив для координат по у для простого падения
41 G = new double [Size];///создаем массив для координат по х для интегрирования по эйлеру
42 Vy = v * sin (a);/// значение скорости по у для метода эйлера
43 Y[0] = 0;///задаем значение по у в нуле
44 G[0] = 0;///задаем значение по у в нуле по эйлеру
45 for (int i = 1; i < Size; i++)///задаем цикл от 1 (для нуля мы задали), чтобы считать координаты
46 {
47 t += shag; ///каждый раз прибавляем по времени шаг
48 Y[i] = v * sin (a) *t - (g * t * t) * 0.5; ///координаты по у для простого падения
49 Vy -= g * shag; ///значение скорости по у для метода эйлера
50 G[i] = G[i-1] + Vy * shag;///у из интегрирования по эйлеру
51 }
52 }
53
54 void SetVerle() ///функция для метода верле
55 {
56 double k = 0.1, m = 0.5; ///коэфф сопротивления водуха, масса тела
57 g = 9.8; /// коэфф свободного падения
58 uint32_t Size1 = 1000000.0; ///размер массива
59 S = new double [Size1]; ///создаем массив для значений по х для метода верле
60 Z = new double [Size1]; ///создаем массив для значений по у для метода верле
61 vx = v * cos(a); ///формулы для вычисления скорости по оси х
62 vy = v * sin(a); ///формулы для вычисления скорости по оси у
63 S[1] = 0; ///значение х метод верле
64 S[0] = -vx * shag; ///значение в нуле
65 Z[1] = 0; ///значение у метод верле
66 Z[0] = -vy * shag; ///значение в нуле
67 for (int i = 0; i < Size1-2; i++) ///задаем цикл
68 {
69 S[i+2] = 2.0 * S[i+1] - S[i] - (k / m) * v * vx * shag * shag;///значения по х для верле
70 vx = 0.5 * ( 1.0 / shag )* ( S[i+2] - S[i]);///считаем значения скорости по оси х
71 Z[i+2] = 2.0 * Z[i+1] - Z[i] - ( g + (k / m) * v * vy ) * shag * shag;///значения по х для верле
72 vy = 0.5 * ( 1.0 / shag )* ( Z[i+2] - Z[i]);///считаем значения скорости по оси х
73 v = sqrt (vx * vx + vy * vy); ///модуль общей скорости
74 }
75 }
76 void SetVerleLast() ///функция для точного метода верле
77 {
78 double k = 0.1, m = 0.5;///коэфф сопротивления водуха, масса тела
79 g = 9.8; /// коэфф свободного падения
80 uint32_t Size2 = 1000000.0; ///размер массива
81 float t = 0; ///время
82 V = new double [Size2]; ///создаем массив для значений по х для точного метода верле
83 U = new double [Size2]; ///создаем массив для значений по у для точного метода верле
84 vx = v * cos(a); ///формулы для вычисления скорости по оси х
85 vy = v * sin(a); ///формулы для вычисления скорости по оси у
86 ///double e = 2.7 ;///значение экспоненты
87 V[0] = 0; ///значение х точный метод верле
88 U[0] = 0; ///значение у точный метод верле
89 for (int i = 1; i < Size2; i++)
90 {
91 t += shag; ///увеличиваем время на шаг
92 V[i] = vx * (m / k) * (1.0 - exp(((-k) / m) * t)); ///значения по х для точного верле
93 U[i] = (m / k) * (vy + g * (m / k)) * (1.0 - (exp(((-k) / m) * t))) - g * t * (m / k);///значения по х для точного верле
94 }
95 }
96
97 public: ///в открытом
98 pad()
99 {
100 X = 0; ///зануляем значения
101 Y = 0;
102 Size = 0;
103 v = 0;
104 shag = 0;
105 b = 0;
106 }
107 pad(double _v, double _shag, double _b) ///конструктор с параметрами
108 {
109 pi = M_PI; ///значение числа пи
110 g = 9.8; ///коэфф свободного падения
111 v = _v;/// присваиваем значения переменных значению параметров в конструкторе
112 shag = _shag;
113 b = _b;
114 a = (pi * b) / 180.0 ; ///вычисляем значение угла в радианах
115 double t = (2.0 * v * sin(a)) / g; /// считаем значение времени
116 Size = abs( t / shag )+1;///ищем значение размера массива
117 SetX(); ///вызываем функции зависящие от параметров конструктора
118 SetY();
119 SetVerle();
120 SetVerleLast();
121 }
122
123 void FilePrint() ///функция записи в файл
124 {
125 ofstream fout("output.txt"); ///открываем файл уже созданный в папке с программой
126 fout << "X: " << " Y: " << " E: " << " G: " << " S: " << " Z: "<< " V: "<< " U: "<<"\n" ; ///выводим стоку с разными названиями массивов, соотв. координатам по х и у различных методов
127 for (int i = 0; i < Size; i++) ///цикл
128 fout << X[i] << " " << Y[i] << " " << E[i] << " " << G[i] << " " << S[i] << " " << Z[i] << " " << V[i] <<" "<< U[i] <<"\n"; ///забивает сами значения массивов
129 fout.close();///закрываем файл
130 };
131 };
132
133 int main()/// основная функция
134 {
135 double shag, b, v; ///шаг, угол в градусах, скорость начальная
136 cout << "vvedite v "; ///просим пользователя ввести значение скорости начальной
137 cin >> v; ///считываем начальную скорость
138 cout << "vvedite ygol ";///просим пользователя ввести угол в градусах
139 cin >> b;/// считываем угол
140 cout << "vvedite shag ";///просим пользователя ввести шаг по времени
141 cin >> shag; ///считываем значение шага
142 pad F1(v, shag, b); ///объявление коструктора, создание функции F1 с переменными v, shag, b
143 F1.FilePrint(); ///вызываем функцию для записи файла
144 }
Описание программы: программа состоит из четырех независимых друг от друга частей:
- Полет тела без сопротивления воздуха;
- Полет тела при линейной зависимости силы сопротивления воздуха от скорости, при котором координаты тела рассчитываются точным методом;
- Полет тела при линейной зависимости силы сопротивления воздуха от скорости, при котором координаты тела рассчитываются методом Верле;
- Полет тела при квадратичной зависимости силы сопротивлении воздуха от скорости, при котором координаты тела рассчитываются методом Верле;
Скачать можно [тут]
Описание программы: программа записывает в четыре файла результаты вычисления:
- Координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
- Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости;
- Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости;
- Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости.
Инструкция : Пользователь вводит начальные данные ( массу, скорость, угол броска, шаг по времени и сопротивление воздуха). Выбираем режим работы программы, после этого в папке с программой создается файл, который требуется открыть программой gnuplot для просмотра графика, построенного на полученных координатах.
Визуализированный результат работы программы
1 #include <iostream>
2 #include <math.h>
3 #include <iomanip>
4 #include <fstream>
5 #include <conio.h>
6 #include <stdio.h>
7
8
9 using namespace std;
10
11 double g = 9.8, Pi = 3.1415; // Задаем две глобальные переменные ускорения свободного падения и числа Pi
12
13 int WoutR(double alpha, double dt, double t, double Yo, double Vo) // Функция, записывающая в файл Throws Without Resistance.txt координаты тела, которое движется без сопротивления
14 {
15 FILE *Coord;
16 Coord = fopen ("Throws Without Resistance.txt", "w");
17 double X = 0, Y = 0; // Координаты начала
18
19 while ( Y >= Yo) // Yo используем для того, чтобы цикл прекратился тогда, когда тело упадет
20 {
21
22 X = Vo*t*cos(alpha);
23 Y = Vo*t*sin(alpha) - (g*t*t)*0.5;
24 t+= dt;
25 if (Y > Yo )
26 fprintf(Coord, "%.3lf \t %.3lf\n", X, Y);
27 else
28 fprintf(Coord, "%.3lf \t %.3lf\n", X, 0.000); // Используем такой else для того, чтобы не получить отрицательную координату
29 }
30
31 }
32
33 int ExactForm(double alpha, double dt, double t, double Yo, double Vo, double R, double m) // Функция, записывающая в файл ExactForm.txt координаты тела, рассчитывающиеся по формлуе точного решения
34 { // для линейной зависимости
35 FILE *Coord;
36 Coord = fopen ("ExactForm.txt", "w");
37 double X, Y = 0, Vx, Vy;
38
39 while ( Y >= Yo) // Использование Yo аналогично использованию в прошлом пункте.
40 {
41
42 X = ((m*Vx)/R) * (1 - exp(((-1)*R*t)/m));
43 Y = (m/R)*((Vy + (g*m)/R)*(1 - exp((-1)*R*t/m))) - (g*t*m)/R;
44 Vx = Vo*cos(alpha);
45 Vy = Vo*sin(alpha);
46 t+= dt;
47 if (Y > Yo )
48 fprintf(Coord, "%.3lf \t %.3lf\n", X, Y);
49 else
50 fprintf(Coord, "%.3lf \t %.3lf\n", X, 0.000); // используется аналогично прошлому пункту
51 }
52 }
53
54 int VerleSq (double alpha, double dt, double t, double Yo, double Xo, double Vo, double R, double m) // Функция, записывающая в файл VerleSq.txt оординаты тела, рассчитывающиеся по формлуе Верле
55 { // для Квадратичной зависимости сопротивления от скорости
56 FILE *Coord;
57 Coord = fopen ("VerleSq.txt", "w");
58
59 double X, Xnext, Xprev, Y, Ynext, Yprev, Vx, Vy, V, Yop, Xop; // X, Y - текущие координаты; Xnext, Ynext - координаты следующего шага; Xprev, Yprev - координаты предыдущего шага.
60 // Xop, Yop - вспомогательные координаты для (-1)-го шага
61
62 Yop = Yo - Vo*sin(alpha)*dt; // Сторки 62-79 используются для просчитывания (-1)-го шага, так как в точке 0;0 у нас нету предыдущего шага
63 Xop = Xo - Vo*cos(alpha)*dt;
64 X = Xo;
65 Y = Yo;
66 Xnext = 2.0*X - Xop - (R/m)*Vo*Vo*cos(alpha)*(dt*dt);
67 Vx = (1.0/(2.0*dt))*(Xnext - Xop);
68 Ynext = 2.0*Y - Yop - (g +(R/m)*Vo*Vo*sin((alpha)))*(dt*dt);
69 Vy = (1.0/(2.0*dt))*(Ynext - Yop);
70 V = sqrt((Vo*cos(alpha)*Vo*cos(alpha)) + (Vo*sin(alpha)*Vo*sin(alpha)));
71
72 fprintf(Coord, "%.3lf \t %.3lf\n", X, Y); // Записываем первую координату в файл
73
74 Xprev = X; // Меняем координаты местами. Так (n-1)-ый шаг становится n-ым шагом, n-ый шаг становится (n+1)-ым шагом. Далее аналогично
75 X = Xnext;
76 Yprev = Y;
77 Y = Ynext;
78
79
80 while (Y >= Yo) // После выполнения строк 62-79 получаем все необходимые данные для выполнения алгоритма.
81 {
82 Xnext = 2.0*X - Xprev - (R/m)*V*Vx*(dt*dt);
83 Vx = (1.0/(2.0*dt))*(Xnext - Xprev);
84 Ynext = 2.0*Y - Yprev - (g +(R/m)*V*Vy)*(dt*dt);
85 Vy = (1.0/(2.0*dt))*(Ynext - Yprev);
86 V = sqrt((Vx*cos(alpha)*Vx*cos(alpha)) + (Vy*sin(alpha) - g*dt)*(Vy*sin(alpha) - g*dt));
87 if (Ynext > Yo )
88 fprintf(Coord, "%.3lf \t %.3lf\n", Xnext, Ynext);
89 else
90
91 fprintf(Coord, "%.3lf \t %.3lf\n", X, 0.000);
92
93 Xprev = X;
94 X = Xnext;
95 Yprev = Y;
96 Y = Ynext;
97 }
98
99 }
100 int VerleL (double alpha, double dt, double t, double Yo, double Xo, double Vo, double R, double m) // Функция, записывающая в файл VerleL.txt оординаты тела, рассчитывающиеся по формлуе Верле
101 { // для линейной зависимости сопротивления от скорости
102 FILE *Coord;
103 Coord = fopen ("VerleL.txt", "w");
104
105 double X, Xnext, Xprev, Y, Ynext, Yprev, Vx, Vy, V,Yop, Xop; // Комментарии аналогичны переменным и формулам в VtrleSq
106
107 Yop = Yo - Vo*sin(alpha)*dt;
108 Xop = Xo - Vo*cos(alpha)*dt;
109 X = Xo;
110 Y = Yo;
111 Xnext = 2.0*X - Xop - (R/m)*Vo*Vo*cos(alpha)*(dt*dt);
112 Vx = (1.0/(2.0*dt))*(Xnext - Xop);
113 Ynext = 2.0*Y - Yop - (g +(R/m)*Vo*Vo*sin((alpha)))*(dt*dt);
114 Vy = (1.0/(2.0*dt))*(Ynext - Yop);
115 V = sqrt((Vo*cos(alpha)*Vo*cos(alpha)) + (Vo*sin(alpha)*Vo*sin(alpha)));
116
117 fprintf(Coord, "%.3lf \t %.3lf\n", X, Y);
118
119 Xprev = X;
120 X = Xnext;
121 Yprev = Y;
122 Y = Ynext;
123
124
125 while (Y >= Yo)
126 {
127 Xnext = 2.0*X - Xprev - (R/m)*Vx*(dt*dt);
128 Vx = (1.0/(2.0*dt))*(Xnext - Xprev);
129 Ynext = 2.0*Y - Yprev - (g +(R/m)*Vy)*(dt*dt);
130 Vy = (1.0/(2.0*dt))*(Ynext - Yprev);
131 if (Ynext > Yo )
132 fprintf(Coord, "%.3lf \t %.3lf\n", Xnext, Ynext);
133 else
134 fprintf(Coord, "%.3lf \t %.3lf\n", Xnext, 0.000);
135
136 Xprev = X;
137 X = Xnext;
138 Yprev = Y;
139 Y = Ynext;
140 }
141
142 }
143
144 int main()
145 {
146 double alpha, Vo, dt, R, m , t = 0, Yo = 0, Xo = 0; // Объявляем переменные: alpha - угол броска; Vo - начальная скорость; dt - шаг по времени; R- коэф. сопротивления; m- масса тела;
147 // t = 0 - начало отсчета времени с 0; Yo = 0, Xo = 0 - координаты начала
148 int i = 0; // переменная для оператора switch
149
150 cout << "Enter start speed:\n";
151 cin >> Vo; // Вводим с клавиатуры начальную скорость
152 cout << "Enter angle in grades ( from 0 to 180 ):\n";
153 cin >> alpha; // Вводим с клавиатуры угол броска в градусах
154 alpha = alpha*Pi / 180; // переводим угол броска из градусов в радианы
155 cout << "Enter mass:\n";
156 cin >> m; // Вводим с клавиатуры массу
157 cout << "Enter precision:\n";
158 cin >> dt; // Вводим с клавиатуры шаг по времени
159 cout << "Enter resistance:\n";
160 cin >> R; // Вводим сопротивление воздуха
161 cout << "Press 1 to draw graph without resistance\n\n"
162 "Press 2 to draw graph in Exact form\n\n"
163 "Press 3 to draw graph in VerleSq form\n\n"
164 "Press 4 to draw graph in VerleL form\n\n"
165 "Press 5 to draw all graphs at the same time\n\n"
166 "Press 0 to quit\n\n";
167 cin >> i;
168 cout << "\nPress any button\n";
169
170
171 FILE *Gnu;
172 Gnu = fopen ("Throws.gp", "w"); // Создаем файл формата gp, который будем открывать программой gnuplot для того, чтобы построить наш график/ки по точкам
173
174 switch ( i )
175 {
176 case 1:
177 {
178 WoutR(alpha,dt,t,Yo,Vo);
179 fprintf(Gnu, "plot \"Throws Without Resistance.txt\" using 1:2 w l");
180 break;
181 }
182 case 2:
183 {
184 ExactForm(alpha,dt,t,Yo,Vo,R,m);
185 fprintf(Gnu, "plot \"ExactForm.txt\" using 1:2 w l");
186 break;
187 }
188 case 3:
189 {
190 VerleSq(alpha,dt,t,Yo,Xo,Vo,R, m);
191 fprintf(Gnu, "plot \"VerleSq.txt\" using 1:2 w l");
192 break;
193 }
194 case 4:
195 {
196 VerleL(alpha,dt,t,Yo,Xo,Vo,R, m);
197 fprintf(Gnu, "plot \"VerleL.txt\" using 1:2 w l");
198 break;
199 }
200 case 5:
201 {
202 WoutR(alpha,dt,t,Yo,Vo);
203 ExactForm(alpha,dt,t,Yo,Vo,R,m);
204 VerleSq(alpha,dt,t,Yo,Xo,Vo,R, m);
205 VerleL(alpha,dt,t,Yo,Xo,Vo,R, m);
206 fprintf(Gnu, "plot \"Throws Without Resistance.txt\" using 1:2 w l, \"ExactForm.txt\" using 1:2 w l, \"VerleSq.txt\" using 1:2 w l, \"VerleL.txt\" using 1:2 w l"); // записываем в Throws.gp названия четырех файлов
207 break;
208 } // с координатами таким образом, чтобы программа gnuplot смогла их увидеть и прочесть
209 case 0:
210 break;
211 default:
212 break;
213 }
214 return 0;
215 }
Описание программы: в программе выполняются четыре метода подсчета координат тела, брошенного под углом к горизонту. Координаты записываются в файл, строятся четыре графика, иллюстрирующие поведение тела при полете. Код написан для определенных начальных условий (для примера), если Вы хотите выполнить расчет для другой конфигурации, внесите изменения в начальные данные программы в самом коде. Начальная скорость: 40 м/с, угол бросания: 45 градусов, коэффициент сопротивления воздуха: 0.023, шаг по времени : 0.1 секунды.
Скачать программу можно здесь
Визуализированный результат работы программы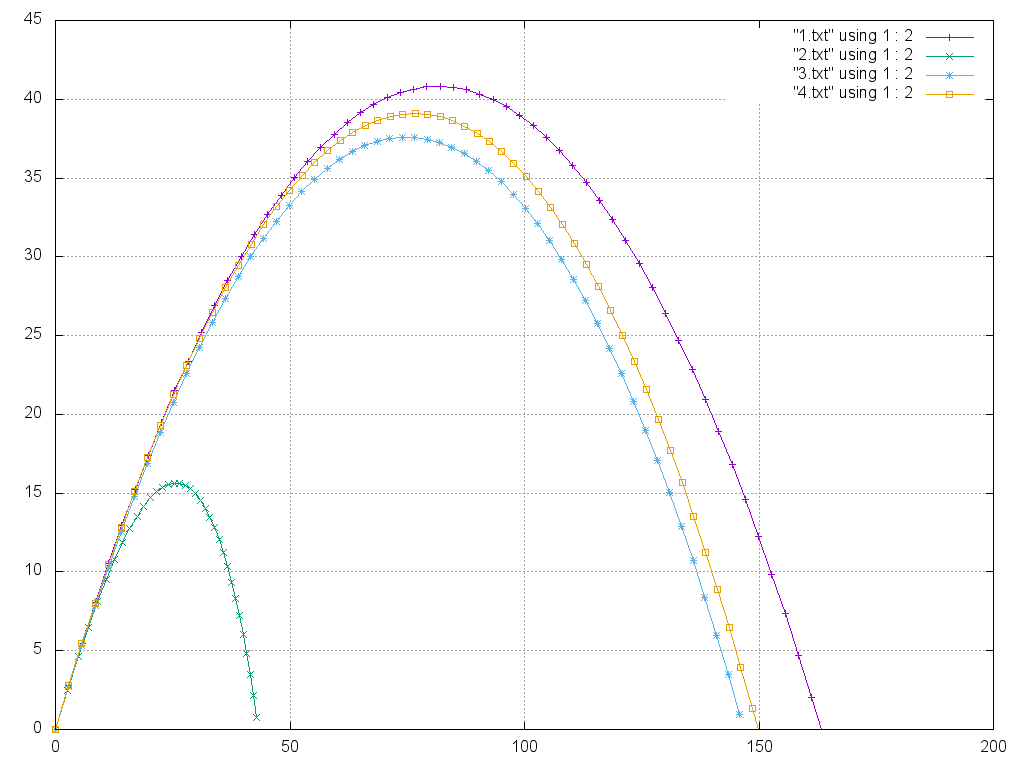
File:graph.png
1 #include <iostream>
2 #include <math.h>
3 #include <iomanip>
4 #include <fstream>
5 #include <conio.h>
6
7
8 using namespace std;
9
10 ofstream outfile;
11
12 double perevod (double angle) //перевод из градусов в радианы
13 {
14 return (angle * M_PI / 180 );
15 }
16
17
18 int main()
19 {
20 //объявление переменных и задание начальных значений
21 double X, Xnext, Xprev, Y, Ynext, Yprev, Vx, Vy, V,
22 m = 1 , dt = 0.1 , g = 9.8,t = 0,
23 ugol = 45, alpha, R = 0.023, Xo = 0, Yo = 0, Vo = 40;
24
25 alpha = perevod (ugol);
26
27 //точное решение для случая движения без сопротивления воздуха
28 Y = Yo;
29 X = Xo;
30
31 outfile.open("1.txt");
32
33 while (Y >= Yo)
34 {
35 X = Xo + Vo * cos(alpha) * t;
36 Vx = Vo * cos(alpha);
37 Y = Yo + Vo * sin(alpha) * t - 0.5 * g * t * t;
38 Vy = Vo * sin(alpha) - g * t;
39 t += dt;
40
41 outfile << X << ' ' << Y << endl;
42 }
43 outfile.close();
44
45 //начальные условия для квадратичной зависимости (метод Верле)
46 Yprev = Yo - Vo*sin(alpha)*dt;
47 Xprev = Xo - Vo*cos(alpha)*dt;
48 X = Xo;
49 Y = Yo;
50 V = Vo;
51 Vx = Vo * cos(alpha);
52 Vy = Vo * sin(alpha);
53
54 outfile.open("2.txt");
55
56 while (Y >= Yo)
57 {
58 Xnext = 2.0 * X - Xprev - (R / m) * V * Vx * (dt * dt);
59 Vx = ( Xnext - Xprev )/ (2.0 * dt);
60 Ynext = 2.0 * Y - Yprev - (g + (R / m) * V * Vy) * (dt * dt);
61 Vy = (Ynext - Yprev)/ (2.0 * dt);
62 V = sqrt(Vy*Vy + Vx*Vx );
63 outfile << X << ' ' << Y << endl;
64
65 Xprev = X;
66 X = Xnext;
67 Yprev = Y;
68 Y = Ynext;
69 }
70 outfile.close();
71
72 //начальные условия для линейной зависимости (метод Верле)
73 Yprev = Yo - Vo*sin(alpha)*dt;
74 Xprev = Xo - Vo*cos(alpha)*dt;
75 X = Xo;
76 Y = Yo;
77 V = Vo;
78 Vx = Vo * cos(alpha);
79 Vy = Vo * sin(alpha);
80
81 outfile.open("3.txt");
82
83 while (Y >= Yo)
84 {
85 Xnext = 2.0 * X - Xprev - (R / m) * Vx * (dt * dt);
86 Vx = ( Xnext - Xprev )/ (2.0 * dt);
87 Ynext = 2.0 * Y - Yprev - (g + (R / m) * Vy) * (dt * dt);
88 Vy = (Ynext - Yprev)/ (2.0 * dt);
89 V = sqrt(Vy*Vy + Vx*Vx );
90 outfile << X << ' ' << Y << endl;
91
92 Xprev = X;
93 X = Xnext;
94 Yprev = Y;
95 Y = Ynext;
96 }
97 outfile.close();
98
99 //точное решения для линейной зависимости
100 Y = Yo;
101 X = Xo;
102 t = 0;
103
104 outfile.open("4.txt");
105
106 while (Y >= Yo)
107 {
108 Vx = Vo * cos(alpha);
109 Vy = Vo * sin(alpha);
110 X = (m * Vx / R)* (1 - exp(-1 * R * t / m));
111 Y = (m/R)*((Vy + g * m / R)*(1 - exp(-1 * R * t / m)) - g * t);
112 t += dt;
113 outfile << X << ' ' << Y << endl;
114 }
115 outfile.close();
116
117 return 0;
118
119 }
Описание программы : программа записывает в четыре файла результаты вычисления:
Координаты, рассчитанные по формуле, при движении без сопротивления воздуха; Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости; Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости; Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости.
Скачивать тут
Описание программы: программа рассчитывает координаты точки при следующих случаях
- Полет тела без сопротивления воздуха;
- Полет тела при линейной зависимости силы сопротивления воздуха от скорости, при котором координаты тела рассчитываются точным методом;
- Полет тела при линейной зависимости силы сопротивления воздуха от скорости, при котором координаты тела рассчитываются методом Верле;
- Полет тела при квадратичной зависимости силы сопротивлении воздуха от скорости, при котором координаты тела рассчитываются методом Верле;
Скачать можно [тут]
Описание программы: программа записывает в четыре файла результаты вычисления:
- Координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
- Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости;
- Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости;
- Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости.
Скачать можно тут.
Визуализированный результат работы программы

- o1 - координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
- o2 - координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости;
- o3 - координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости;
- o4 - координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости.
Для тела с массой 10,сопротивлением воздуха 1, угол бросания 30°, начальная скорость 30 м/с, ускорение свободного падения 9.8 м/c^2;
Примечание: графики o1 и o2 намеренно посчитаны с малой точностью, чтобы графики не сливались.
Файл "main.cpp"
1 #include <iostream>
2 #include <math.h>
3 #include "Vector.h"
4 #include <cstring>
5 #include <cmath>
6 #include <malloc.h>
7 #include <fstream>
8
9 using namespace std;
10
11 int n = 100;
12 ofstream outfile;
13
14 class Ball //класс бросаемого тела
15 {
16 private:
17 double angle,m,k; //угол броска,масса,коэффицент сопротивления воздуха
18 Vector3D r,v,a; //радиус-вектор,вектор скорости,ускорения
19 public:
20
21 //задание начальных параметров через угол,начальное положение,скорость и ускорение,с которым движется тело. Без сопротивления воздуха
22 Ball(double _angle, Vector3D _r, Vector3D _v, Vector3D _a)
23 {
24 angle = _angle;
25 r = _r;
26 v = _v;
27 a = _a;
28 }
29
30 //задание начальных параметров через угол,начальное положение,скорость и ускорение,с которым движется тело. Без сопротивления воздуха
31 Ball(double _angle, double _m, double _k, Vector3D _r, Vector3D _v, Vector3D _a)
32 {
33 angle = _angle;
34 r = _r;
35 v = _v;
36 a = _a;
37 m = _m;
38 k = _k;
39 }
40
41 //точная формула зависимости координаты от времени
42 Vector3D positionReal(double t)
43 {
44 double c1 = m/k,c2 = fabs(a.y)*c1, c3 = exp(-t/c1), c4 = c2*t;
45 return MakeVector(v.x*c1*(1 - c3), c1*(v.y + c2)*(1 - c3) - c4 , 0 );
46 }
47
48 //вывод положения на экран
49 void writePosToScreen()
50 {
51 cout << r.x << " " << r.y << " " << r.z << endl;
52 }
53
54 //вывод положения в файл
55 void writePosToFile(char s[])
56 {
57 outfile.open(s,ios :: app);
58 outfile << r.x << " " << r.y << endl;
59 outfile.close();
60 }
61
62 //вывод произвольного вектора на экран
63 void WVTS(Vector3D v)
64 {
65 cout.width(15);
66 cout << v.x;
67 cout.width(15);
68 cout << v.y;
69 cout.width(15);
70 cout << v.z << endl;
71 }
72
73 //вывод произвольного вектора в файл
74 void WVTF(Vector3D v,char s[])
75 {
76 outfile.open(s,ios :: app);
77 outfile << v.x << " " << v.y << endl;
78 outfile.close();
79 }
80
81 //"пересчет" координаты по Верле(Линейная зависмость)
82 void changeR(Vector3D r1, double dt)
83 {
84 r = MakeVector(2 * r.x - r1.x - k/m*v.x*dt*dt,2*r.y - r1.y - (abs(a.y) + k/m*v.y)*dt*dt, 0 );
85 }
86
87 //"пересчет" координаты по Верле(Квадратичная зависимость)
88 void changeRSQ(Vector3D r1, double dt)
89 {
90 r = MakeVector(2 * r.x - r1.x - k/m*Length(v)*v.x*dt*dt,2*r.y - r1.y - (abs(a.y) + k/m*Length(v)*v.y)*dt*dt, 0 );
91 }
92 //пересчет скорости по Верле
93 void changeV(Vector3D r1,double dt)
94 {
95 v =VS((VmV(r,r1)),1/(2*dt));
96 }
97
98 //рассчет предыдущегт к 0ому элементу
99 Vector3D MR1(double dt)
100 {
101 return MakeVector(r.x - v.x * dt,r.y - v.y * dt,0);
102 }
103
104 //возращает координату тела
105 Vector3D getR()
106 {
107 return r;
108 }
109
110 //рассчет времени полета
111 double TimeOfFly()
112 {
113 return (2*Length(v)*sin(angle)/Length(a));
114 }
115
116 //рассчет координаты по точной формуле. без сопротивления воздуха.
117 Vector3D position(double t)
118 {
119 return MakeVector(r.x + v.x*t + a.x*t*t/2,r.y + v.y*t + a.y*t*t/2,r.z + v.z*t + a.z*t*t/2);
120 }
121
122 };
123
124 int main()
125 {
126 //задание начальных параметров
127 Vector3D g = {0,-9.8,0};
128 double a,dt = 0;
129 char s[20];
130
131 // cin >> dt;
132
133 dt = 0.1;
134 a = (M_PI * 30)/180;
135 Ball b1(a, MakeVector(0,0,0),MakeVector(30,a),g);
136
137 double tof = b1.TimeOfFly()+1; //единичка прибавлена,чтобы график красивым был
138
139 //Без сопротивления возлуха
140 strcpy(s,"");
141 strcat(s, "o1.txt");
142 outfile.open(s, ios :: trunc);
143 outfile.close();
144 for (double i = 0; i <= tof; i += dt)
145 {
146 b1.WVTS(b1.position(i));
147 b1.WVTF(b1.position(i), s);
148 }
149
150
151 //Верле(Линейная зависимость)
152 dt = 0.1;
153 a = (M_PI * 30)/180;
154 Ball b2(a,10 , 1, MakeVector(0,0,0),MakeVector(30,a),g);
155
156 strcpy(s,"");
157 strcat(s, "o2.txt");
158 outfile.open(s,ios :: trunc);
159 outfile.close();
160 Vector3D r1 = b2.MR1(dt),rp;
161 for (double i = 0; i <= 20; i += dt)
162 {
163 rp = b2.getR();
164 b2.writePosToFile(s);
165 b2.writePosToScreen();
166 b2.changeR(r1,dt);
167 b2.changeV(r1,dt);
168 r1.x = rp.x;
169 r1.y = rp.y;
170 }
171
172 //Точное решение (Линейная зависимость)
173 dt = 0.1;
174 a = (M_PI * 30)/180;
175 Ball b3(a,10 , 1, MakeVector(0,0,0),MakeVector(30,a),g);
176
177 strcpy(s,"");
178 strcat(s, "o3.txt");
179 outfile.open(s, ios :: trunc);
180 outfile.close();
181 for (double i = 0; i <= 20; i += dt)
182 {
183 b3.WVTS(b3.positionReal(i));
184 b3.WVTF(b3.positionReal(i), s);
185 }
186
187
188 //Верле (Квадратичная зависимость)
189 dt = 0.1;
190 a = (M_PI * 30)/180;
191 Ball b4(a,10 , 1, MakeVector(0,0,0),MakeVector(30,a),g);
192
193 strcpy(s,"");
194 strcat(s, "o4.txt");
195 outfile.open(s, ios :: trunc);
196 outfile.close();
197 r1 = b4.MR1(dt);
198 for (double i = 0; i <= 20; i += dt)
199 {
200 rp = b4.getR();
201 b4.writePosToFile(s);
202 b4.writePosToScreen();
203 b4.changeRSQ(r1,dt);
204 b4.changeV(r1,dt);
205 r1.x = rp.x;
206 r1.y = rp.y;
207 }
208
209 return 0;
210 }
Файл "Vector.h"
1 #ifndef VECTOR_H_INCLUDED
2 #define VECTOR_H_INCLUDED
3
4 struct Vector3D
5 {
6 double x,y,z;
7 };
8
9 Vector3D VmV(Vector3D v1,Vector3D v2) //векторное вычитание
10 {
11 Vector3D v = {v1.x - v2.x,v1.y - v2.y,v1.z - v2.z };
12 return v;
13 };
14 Vector3D VpV(Vector3D v1,Vector3D v2) //векторное сложение
15 {
16 Vector3D v = {v1.x + v2.x,v1.y + v2.y,v1.z + v2.z };
17 return v;
18 }
19
20 double VV(Vector3D v1,Vector3D v2) //скалярное умножение
21 {
22 return (v1.x*v2.x + v1.y*v2.y + v1.z*v2.z);
23 }
24
25 Vector3D VxV(Vector3D v1,Vector3D v2) //векторное умножение
26 {
27 Vector3D v = {v1.y*v2.z - v1.z*v2.y, v1.z*v2.x - v1.x*v2.z,v1.x*v2.y - v1.y*v2.x};
28 return v;
29 }
30
31 bool Kol(Vector3D v1,Vector3D v2)
32 {
33 return ((v1.x/v2.x == v1.y/v2.y)&&(v1.z/v2.z == v1.y/v2.y))? true:false;
34 }
35
36 Vector3D VS(Vector3D v1, double s)
37 {
38 Vector3D v = {v1.x*s, v1.y*s, v1.z*s};
39 return v;
40 }
41
42 double Length(Vector3D v1)
43 {
44 return sqrt(VV(v1,v1));
45 }
46
47 Vector3D MakeVector(double x,double y,double z)
48 {
49 Vector3D v = {x,y,z};
50 return v;
51 }
52
53 Vector3D MakeVector(double length,double angle)
54 {
55 Vector3D v = {length * cos(angle), length * sin(angle),0};
56 return v;
57 }
58
59 double Proection(Vector3D base, Vector3D dir)
60 {
61 return (VV(base,dir)/Length(base));
62 }
63 #endif // VECTOR_H_INCLUDED
Описание программы : программа записывает в четыре файла результаты вычисления:
Координаты, рассчитанные по формуле, при движении без сопротивления воздуха; Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости; Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости; Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости.
Краткая инструкция:
В окне консоли пользователю предлагается вывести следующие значения: начальную скорость , угол и шаг. После этого полученные в результате работы программы данные выводятся в файл.
Описание: Пользователя попросят ввести начальную скорость,угол бросания,массу тела и коэф.сопротивления воздуха,тогда программа запишет в 4 разных файла результаты следующих вычислений:
- Координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
- Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости;
- Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости.
- Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости;
Графики полученные при скорости =10 m/c;угле = 30 градусам;массе=10 кг;коэф.сопротивления=1;
1 #include<iostream>
2 using namespace std;
3 #define N 1
4 #define PI 3.14159265
5 #include <fstream>
6 #include<cmath>
7 double g=9.8;
8 double step=0.01;
9 #include<math.h>
10
11 void Func(double v,double r)//1.Координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
12
13 {
14 double x,y;
15
16 ofstream fout;//открытие файла
17 fout.open("C:\\Users\\Light\\Desktop\\1.txt");//указываем путь записи
18 cout<<"method1"<<endl;
19
20 for(double t=0.01;t<N;t=t+0.01)
21 {
22 y=v*t*sin(r*PI/ 180)-g*t*t/2;//координата y
23 x=v*t*cos(r*PI / 180);//координата х
24
25 fout<<x<<" ";//запись в файл х
26 cout<<"X="<<x<<endl;//вывод на экран
27 fout<<y<<" ";//запись в файл
28 cout<<"Y="<<y<<endl<<endl;//вывод на экран
29 fout<<endl;
30 }
31 }
32
33 void Verle1( double n,double m ,double v0,double r)//Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости;
34
35 {
36 double x,y,x0=0,y0=0,xn_1,yn_1;//x0,y0=Xn,Yn начальные значения;xn_1=X(n-1);yn_1=Y(n-1);
37
38 double vx=v0*cos(r*PI / 180);//рассчитваем Vn для первого случая n=0 для x
39 double vy=v0*sin(r*PI/ 180)-g*step;//рассчитваем Vn для первого случая n=0 для y
40
41 xn_1=x0-vx*step;//X(n-1) для первого случая n=0
42 yn_1=y0-vy*step;//Y(n-1) для первого случая n=0
43 ofstream fout;//открытие файла
44 fout.open("C:\\Users\\Light\\Desktop\\2.txt");//путь записи в файл
45 cout<<"Verle1"<<endl<<endl;
46 for(double t=0.02;t<N;t=t+step)
47 {
48 x=2*x0-xn_1-(n*vx*step*step)/m;//считаем Хn+1
49 vx=(x-xn_1)/(2*step);
50 xn_1=x0;//для следущего шага Xn-1=Xn
51 x0=x;//для следущего шага Xn=Xn+1
52
53 y=2*y0-yn_1-(g+(n*vy)/m)*step*step;//Yn+1
54 vy=(y-yn_1)/(2*0.01);//скорость
55 yn_1=y0;//для следущего шага Yn-1=Yn
56 y0=y;//для следущего шага Yn=Yn+1
57 cout<<"X="<<x<<endl;
58 cout<<"Y="<<y<<endl<<endl;
59 fout<<x<<" ";
60 fout<<y<<" ";
61 fout<<endl;
62
63
64 }
65 }
66
67 void Verle2( double n,double m ,double v0,double r)//3.Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости.
68
69 {
70 double x,y,x0=0,y0=0,xn_1,yn_1,v;//x0,y0=Xn,Yn начальные значения;xn_1=X(n-1);yn_1=Y(n-1);
71
72 double vx=v0*cos(r*PI / 180);//рассчитваем Vn для первого случая n=0 для x
73 double vy=v0*sin(r*PI/ 180)-g*step;//рассчитваем Vn для первого случая n=0 для y
74
75 xn_1=x0-vx*step;//X(n-1) для первого случая n=0
76 yn_1=y0-vy*step;//Y(n-1) для первого случая n=0
77 ofstream fout;//открытие файла
78 fout.open("C:\\Users\\Light\\Desktop\\3.txt");//путь записи
79 cout<<"Verle2"<<endl<<endl;
80 for(double t=0.02;t<N;t=t+step)
81 {
82
83 v=sqrt(vx*vx+vy*vy);//скорость V
84
85 x=2*x0-xn_1-(n*v*vx*step*step)/m;//Xn+1
86 vx=(x-xn_1)/(2*step);//скорость Vx
87 xn_1=x0;//для следущего шага Xn-1=Xn
88 x0=x;//для следущего шага Xn=Xn+1
89
90 y=2*y0-yn_1-(g+(n*vy*v)/m)*step*step;//Yn+1
91 vy=(y-yn_1)/(2*0.01);//скорость Vy
92 yn_1=y0;//для следущего шага Yn-1=Yn
93 y0=y;//для следущего шага Yn=Yn+1
94 cout<<"X="<<x<<endl;
95 cout<<"Y="<<y<<endl<<endl;
96 fout<<x<<" ";
97 fout<<y<<" ";
98 fout<<endl;
99 }
100
101 }
102
103 void method4(double n,double m ,double v0,double r)//Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости;
104 {
105 double x,y,x0=0,y0=0;//x0,y0 начальные значения;
106
107 double vx=v0*cos(r*PI / 180);//рассчитваем Vx
108 double vy=v0*sin(r*PI/ 180)-g*step;//рассчитваем Vy
109
110 ofstream fout;//открытие файла
111 fout.open("C:\\Users\\Light\\Desktop\\4.txt");
112 cout<<"4"<<endl<<endl;
113 for(double t=0.01;t<N;t=t+step)
114 {
115 x=x0+m*vx*(1-(exp((-1*n)*t/m)))/n;//координата х
116
117 y = y0+(m/n)*((vy + g * m / n)*(1 - exp(-1 * n * t / m))) - g * t*m/n;//координата у
118
119 //вывод в файл и на экран
120 cout<<"X="<<x<<endl;
121 cout<<"Y="<<y<<endl<<endl;
122 fout<<x<<" ";
123 fout<<y<<" ";
124 fout<<endl;
125
126 }
127 }
128
129 int main(void)
130 {
131
132 double v0,r,m,n;//v0-начальная скорость,r-угол в градусах,m-масса;n-коэф.сопротивления ветра
133
134 cout<<"Enter start speed:"<<endl;
135 cin>>v0;
136 cout<<"Enter angle less than 90 deg:"<<endl;
137 cin>>r;
138 cout<<"Enter mass:"<<endl;
139 cin>>m;
140 cout<<"Coefficient of resistance:"<<endl;
141 cin>>n;
142
143 Func(v0,r);
144 Verle1(n,m,v0,r);
145 Verle2(n,m,v0,r);
146 method4(n,m,v0,r);
147
148
149
150 int k;
151 cin>>k;
152 return 0;
153 }
Скачать можно тут.
Описание программы: Программа рассчитывает координаты полета тела по х и у. Как и в программе шахмат и интерполяции, здесь представлено меню выбора функций. Вы вводите начальные координаты, начальную скорость и угол полета(например, мяча или снаряда)(Нет смысла вводить величину скорости света, так как парабола вряд ли получится). Затем Вы выбираете в меню "вариант" сопротивления воздуха, после чего вводите массу тела и коэффициент сопротивления среды(без сопротивления воздуха этим можно пренебречь). Программа выводит массив точек и сохраняет их в текстовый файл. Эти точки - координаты полета до тех пор, пока значения y не станет ОТРИЦАТЕЛЬНЫМИ... Это мой первый проект по моделированию, спасибо за предоставленную возможность попрактиковаться. Скачать можно [тут]
Нарядчиков Александр
Инструкция: Пользователю достаточно просто запустить программу.
Описание программы: В комнате скачут 4 мячика, первый двигается без сопротивления воздуха, второй двигается с квадратичной зависимостью сопротивления воздуха от скорости (Метод Верле), третий двигается с линейной зависимостью сопротивления воздуха от скорости (точное решение), четвертый двигается с линейной зависимостью сопротивления воздуха от скорости (Метод Верле).
Описание алгоритма: Программа реализована с помощью системы анимации(class anim), используя библиотеки OpenGl и GLUT. Изменения координат мячей проходят в режиме реального времени в векторной форме.
"T06BALL.CPP"
1 /* FILENAME: T06BALL.CPP
2 * LAST UPDATE: 17.01.2016
3 */
4
5 #include "ANIM.H"
6 #include "SAMPLE.H"
7
8 /* Main function */
9 void main( void )
10 {
11 // Получение единственного экземпляра класса анимации
12 sagl::anim &My = sagl::anim::Get();
13
14 // Шар, летящий без сопротивлением воздуха
15 for (int i = 0; i < 1; i++)
16 My << new ball(Pi / 6, 10 + i);
17
18 // Шар, летящий с сопротивлением воздуха
19 // Координаты получены методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости
20 for (int i = 0; i < 1; i++)
21 My << new ball_air(Pi / 6, 10 + i, 10, 0.01);
22
23 // Шар, летящий с сопротивлением воздуха
24 // Координаты получены из точного решения при линейной зависимости силы сопротивлении воздуха от скорости
25 for (int i = 0; i < 1; i++)
26 My << new ball_air_2(Pi / 6, 10 + i, 10, 0.01);
27
28 // Шар, летящий с сопротивлением воздуха
29 // Координаты получены методом Верле при линейной зависимости силы сопротивлении воздуха от скорости
30 for (int i = 0; i < 1; i++)
31 My << new ball_air_3(Pi / 6, 10 + i, 10, 0.01);
32
33 // Запуск главного цикла
34 My.Run();
35 } // End of 'main' function
36
37 // END OF 'T43ANIM.CPP' FILE
"ANIM.CPP"
1 /* FILENAME: ANIM.CPP
2 * LAST UPDATE: 17.01.2016
3 */
4
5 #include <stdio.h>
6 #include <stdlib.h>
7 #include <time.h>
8
9 #include "ANIM.H"
10
11 // Единственный экземпляр класса
12 sagl::anim sagl::anim::Instance;
13
14 /* Reshape function */
15 // Стандартная функция, вызываемая при изменении размеров окна
16 void sagl::anim::Reshape( int W, int H )
17 {
18 // Установка области просмотра - все окно
19 glViewport(0, 0, W, H);
20 Instance.WinW = W;
21 Instance.WinH = H;
22 double ratio_x = 1, ratio_y = 1;
23 if (W > H)
24 ratio_x = (double)W / H;
25 else
26 ratio_y = (double)H / W;
27 double Size = 1, Near = 1, Far = 500;
28 // Установка системы координат "камеры"
29 glMatrixMode(GL_PROJECTION);
30 glLoadIdentity();
31 glFrustum(-Size * ratio_x, Size * ratio_x,
32 -Size * ratio_y, Size * ratio_y,
33 Near, Far);
34 // Установка "мировой" СК в состояние без преобразований
35 glMatrixMode(GL_MODELVIEW);
36 } // End of 'Reshape' function
37
38 /* Timer function */
39 // Подсчет времени
40 void sagl::anim::Timer( void )
41 {
42 long Time = clock();
43
44 if (IsPause)
45 DeltaTime = 0, PauseTime += Time - OldTime;
46 else
47 DeltaTime = (Time - OldTime) / (double)CLOCKS_PER_SEC;
48 OldTime = Time;
49
50 SyncTime = (Time - PauseTime - StartTime) / (double)CLOCKS_PER_SEC;
51 } /* End of 'Timer' function */
52
53 /* Display function */
54 // Стандартная функция, вызываемая при перерисовке окна
55 void sagl::anim::Display( void )
56 {
57 // Запуск времени
58 Instance.Timer();
59 // Очищаем цветовой буфер для создания нового изображения
60 glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
61
62 glLoadIdentity();
63 // Позиционирование СК
64 gluLookAt(-40, 0, 0, 0, 0, 0, 0, 1, 0);
65
66 // Отрисовка объектов
67 Instance.Render();
68
69 glFinish();
70 // Копируем вторичный буфер в окно
71 glutSwapBuffers();
72 // Вызываем функцию обновления кадра
73 glutPostRedisplay();
74 } // End of 'Display' function
75
76 /* Keyboard function */
77 // Стандартная функция, вызываемая при нажатие клавиш на клавиатуре
78 void sagl::anim::Keyboard( unsigned char Key, int X, int Y )
79 {
80 // Выход из программы
81 if (Key == 27)
82 exit(0);
83 // Открытие программы в полном экране
84 else if (Key == 'f')
85 glutFullScreen();
86 // Пауза
87 else if (Key == 'p' || Key == 'P')
88 Instance.IsPause = !Instance.IsPause;
89 } // End of 'Keyboard' function
90
91 sagl::anim::anim( void ) : IsPause(false), SyncTime(0), DeltaTime(0),
92 StartTime(clock()), OldTime(StartTime), PauseTime(0), StockSize(0)
93 {
94 // Инициализации OpenGL и GLUT
95 glutInitDisplayMode(GLUT_RGB | GLUT_DOUBLE | GLUT_DEPTH);
96
97 // Задача размеров и позиции окна
98 glutInitWindowPosition(0, 0);
99 glutInitWindowSize(700, 700);
100 // Создание окна
101 glutCreateWindow("T06BALL");
102
103 // Установка функций 'обратного вызова'
104 glutDisplayFunc(Display);
105 glutKeyboardFunc(Keyboard);
106 glutReshapeFunc(Reshape);
107
108 // Установка цвета закраски фона
109 glClearColor(0.3, 0.5, 0.7, 1);
110 // Включение буфера глубины
111 glEnable(GL_DEPTH_TEST);
112 // Включение режима вычисления цвета согласно освещенности от источников света
113 glEnable(GL_LIGHTING);
114 // Включение источника света
115 glEnable(GL_LIGHT0);
116 // Включение упрощенного режима освещенности для простого способа описания свойств поверхности
117 glEnable(GL_COLOR_MATERIAL);
118 // Приведение нормалей к единичной длине
119 glEnable(GL_NORMALIZE);
120 }
121
122 // Деструктор
123 sagl::anim::~anim( void )
124 {
125 // Чистка памяти
126 for (int i = 0; i < StockSize; i++)
127 delete Stock[i];
128 }
129
130 /* Render function */
131 // Отрисовка объектов
132 void sagl::anim::Render( void )
133 {
134 for (int i = 0; i < StockSize; i++)
135 Stock[i]->Render(*this);
136 } // End of 'Render' function
137
138 /* Run function */
139 // Запуск главного цикла
140 void sagl::anim::Run( void )
141 {
142 // Запуск основного цикла построения
143 glutMainLoop();
144 } // End of 'Run' function
145
146 // END OF 'ANIM.CPP' FILE
"ANIM.H"
1 /* FILENAME: ANIM.H
2 * LAST UPDATE: 17.01.2016
3 */
4
5 #ifndef __ANIM_H_
6 #define __ANIM_H_
7
8 #include <stdio.h>
9 #include <stdlib.h>
10 #include <time.h>
11
12 #include <GL\glut.h>
13
14 #include "VEC.H"
15
16 // Константы
17 #define Pi 3.14159265358979323846
18 #define E 2.71828182845904523536
19
20 // Собственное пространство имен 'sagl'
21 namespace sagl
22 {
23 // Объявления класса анимации наперед
24 class anim;
25
26 // Функции получения случайных чисел
27 inline double r0( void )
28 {
29 return rand() / (double)RAND_MAX;
30 }
31 inline double r1( void )
32 {
33 return 2.0 * rand() / RAND_MAX - 1;
34 }
35
36 // Класс объектов
37 class object
38 {
39 public:
40 // Вектора перемещения и скоростей
41 vec P, V, AbsV;
42
43 // Конструктор
44 object( void ) : P(vec::Rnd1()), V(vec::Rnd()), AbsV(V)
45 {
46 }
47
48 // Отрисовка объектов
49 virtual void Render( anim &Ani )
50 {
51 } // End of 'Render' function
52 }; // end of 'object' class
53
54 // Класс анимации
55 class anim
56 {
57 private:
58 // Функции 'обратного вызова'
59 static void Display( void );
60 static void Keyboard( unsigned char Key, int X, int Y );
61 static void Reshape( int W, int H );
62
63 // Единственный экземпляр класса
64 static anim Instance;
65
66 // Конструктор
67 anim( void );
68
69 // Максимальное количество объектов
70 static const int Max = 100;
71 // 'Контейнер' объектов
72 object *Stock[Max];
73 // Размер 'контейнера' объектов
74 int StockSize;
75
76 // Переменные, хранящие время в секундах
77 long StartTime, OldTime, PauseTime;
78
79 // Отрисовка объектов
80 void Render( void );
81
82 // Подсчет времени
83 void Timer( void );
84 public:
85 // Добавление объектов в 'контейнер'
86 anim & operator<<( object *Obj )
87 {
88 if (StockSize < Max )
89 Stock[StockSize++] = Obj;
90 else
91 delete Obj;
92
93 return *this;
94 }
95
96 // Ширина и высота окна
97 int WinW, WinH;
98
99 // Переменные, хранящие время в секундах
100 double SyncTime, DeltaTime;
101
102 // Переменная, отвечающая за паузу
103 bool IsPause;
104
105 // Деструктор
106 ~anim( void );
107
108 // Запуск главного цикла
109 void Run( void );
110
111 // Метод, возвращающий переменную - единственный экземпляр данного типа
112 static anim & Get( void )
113 {
114 return Instance;
115 }
116 }; // end of 'anim' class
117 } // end of 'sagl' namespace
118
119 #endif /*__ANIM_H_ */
120
121 // END OF 'ANIM.H' FILE
"VEC.H"
1 /* FILENAME: VEC.H
2 * LAST UPDATE: 17.01.2016
3 */
4
5 #ifndef __VEC_H_
6 #define __VEC_H_
7
8 #include <stdlib.h>
9 #include <math.h>
10
11 // Собственное пространство имен 'sagl'
12 namespace sagl
13 {
14 // Класс векторов
15 class vec
16 {
17 public:
18 // Координаты вектора
19 double X, Y, Z;
20
21 // Конструктор
22 vec( void ) : X(0), Y(0), Z(0)
23 {
24 }
25
26 // Конструктор
27 vec( double A, double B, double C ) : X(A), Y(B), Z(C)
28 {
29 }
30
31 // Функции получения случайных чисел
32 static double R0( void )
33 {
34 return rand() / (double)RAND_MAX;
35 }
36
37 static double R1( void )
38 {
39 return 2 * rand() / (double)RAND_MAX - 1;
40 }
41
42 // Функции получения случайных векторов
43 static vec Rnd( void )
44 {
45 return vec(R0(), R0(), R0());
46 }
47
48 static vec Rnd1( void )
49 {
50 return vec(R1(), R1(), R1());
51 }
52
53 vec operator+( vec V )
54 {
55 return vec(X + V.X, Y + V.Y, Z + V.Z);
56 }
57
58 vec operator*( double t )
59 {
60 return vec(X * t, Y * t, Z * t);
61 }
62
63 vec & operator+=( const vec &V )
64 {
65 X += V.X;
66 Y += V.Y;
67 Z += V.Z;
68
69 return *this;
70 }
71
72 // Длина вектора
73 double operator!(void) const
74 {
75 return sqrt(X * X + Y * Y + Z * Z);
76 } /* end of 'operator!' function */
77 }; // end of 'vec' class
78 } // end of 'sagl' namespace
79
80 #endif /*__VEC_H_ */
81
82 // END OF 'VEC.H' FILE
"SAMPLE.H"
1 /* FILENAME: SAMPLE.H
2 * LAST UPDATE: 17.01.2016
3 */
4
5 #ifndef __SAMPLE_H_
6 #define __SAMPLE_H_
7
8 #include <math.h>
9
10 #include "ANIM.H"
11
12 // Шар, летящий без сопротивлением воздуха
13 class ball : public sagl::object
14 {
15 private:
16 double angle, v; // угол вектора скорости к горизонту; модуль скорости
17 public:
18 // Конструктор
19 ball( void ) : angle(Pi / 3), v(1)
20 {
21 P = sagl::vec(sagl::r0() + 5, 5, 0);
22 V.X = 0;
23 V.Y = sin(angle) * v;
24 V.Z = cos(angle) * v;
25 }
26
27 // Конструктор
28 ball( double angle1, double v1 ) : angle(angle1), v(v1)
29 {
30 P = sagl::vec(sagl::r0() + 5, 5, 0);
31 V.X = 0;
32 V.Y = sin(angle) * v;
33 V.Z = cos(angle) * v;
34 }
35
36 // Отрисовка объекта
37 void Render( sagl::anim &Ani )
38 {
39 // Вектор ускорения свободного падения
40 sagl::vec g = sagl::vec(0, -9.8, 0);
41 // Размер комнаты
42 double Size = 120;
43
44 // Изменение вектора скорости
45 V += g * Ani.DeltaTime;
46 // Изменение вектора перемещения
47 P += V * Ani.DeltaTime;
48
49 // Ограничения - стенки
50 if (P.X > Size / 4)
51 V.X = -fabs(V.X);
52 if (P.X < -Size / 4)
53 V.X = fabs(V.X);
54
55 if (P.Y > Size / 4)
56 V.Y = -fabs(V.Y);
57 if (P.Y < -Size / 4)
58 V.Y = fabs(V.Y);
59
60 if (P.Z > Size / 4)
61 V.Z = -fabs(V.Z);
62 if (P.Z < -Size / 4)
63 V.Z = fabs(V.Z);
64
65 // Запоминание состояния изменения текущей СК
66 glPushMatrix();
67
68 // Рисование стенок
69 glutWireCube(Size / 2);
70 // Задача перемещения мяча
71 glTranslated(P.X, P.Y, P.Z);
72 // Цвет мяча
73 glColor3d(0, 1, 0);
74 // Рисование мяча
75 glutSolidSphere(0.5, 30, 30);
76
77 // Восстановление последнего запоминания состояния изменения текущей СК
78 glPopMatrix();
79 }
80 }; // end of 'ball' class
81
82 // Шар, летящий с сопротивлением воздуха
83 // Координаты получены методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости
84 class ball_air : public sagl::object
85 {
86 private:
87 double angle, v, m, n;
88 public:
89 // Конструктор
90 ball_air( void ) : angle(Pi / 3), v(1), m(1), n(0.1)
91 {
92 P = sagl::vec(sagl::r0() + 5, 5, 0);
93 V.X = 0;
94 V.Y = sin(angle) * v;
95 V.Z = cos(angle) * v;
96 }
97
98 // Конструктор
99 ball_air( double angle1, double v1, double m1, double n1 ) : angle(angle1), v(v1), m(m1), n(n1)
100 {
101 P = sagl::vec(sagl::r0() + 5, 5, 0);
102 V.X = 0;
103 V.Y = sin(angle) * v;
104 V.Z = cos(angle) * v;
105 }
106
107 // Отрисовка объекта
108 void Render( sagl::anim &Ani )
109 {
110 // Вектор ускорения свободного падения и вектор полного ускорения
111 sagl::vec g = sagl::vec(0, -9.8, 0), a;
112 // Размер комнаты
113 double Size = 120;
114
115 // Изменение вектора ускорения
116 a = sagl::vec(0, g.Y - n / m * !V * V.Y, -n / m * !V * V.Z);
117
118 // Изменение вектора скорости
119 V += a * Ani.DeltaTime;
120 // Изменение вектора перемещения
121 P += V * Ani.DeltaTime;
122
123 // Ограничения - стенки
124 if (P.X > Size / 4)
125 V.X = -fabs(V.X);
126 if (P.X < -Size / 4)
127 V.X = fabs(V.X);
128
129 if (P.Y > Size / 4)
130 V.Y = -fabs(V.Y);
131 if (P.Y < -Size / 4)
132 V.Y = fabs(V.Y);
133
134 if (P.Z > Size / 4)
135 V.Z = -fabs(V.Z);
136 if (P.Z < -Size / 4)
137 V.Z = fabs(V.Z);
138
139 // Запоминание состояния изменения текущей СК
140 glPushMatrix();
141
142 // Рисование стенок
143 glutWireCube(Size / 2);
144 // Задача перемещения мяча
145 glTranslated(P.X, P.Y, P.Z);
146 // Цвет мяча
147 glColor3d(1, 0, 0);
148 // Рисование мяча
149 glutSolidSphere(0.5, 30, 30);
150
151 // Восстановление последнего запоминания состояния изменения текущей СК
152 glPopMatrix();
153 }
154 }; // end of 'ball_air' class
155
156 // Шар, летящий с сопротивлением воздуха
157 // Координаты получены из точного решения при линейной зависимости силы сопротивлении воздуха от скорости
158 class ball_air_2 : public sagl::object
159 {
160 private:
161 double angle, v, m, n;
162 public:
163 // Конструктор
164 ball_air_2( void ) : angle(Pi / 3), v(1), m(1), n(0.1)
165 {
166 P = sagl::vec(sagl::r0() + 5, 5, 0);
167 V.X = 0;
168 V.Y = sin(angle) * v;
169 V.Z = cos(angle) * v;
170 }
171
172 // Конструктор
173 ball_air_2( double angle1, double v1, double m1, double n1 ) : angle(angle1), v(v1), m(m1), n(n1)
174 {
175 P = sagl::vec(sagl::r0() + 5, 5, 0);
176 V.X = 0;
177 V.Y = sin(angle) * v;
178 V.Z = cos(angle) * v;
179 }
180
181 // Отрисовка объекта
182 void Render( sagl::anim &Ani )
183 {
184 // Вектор ускорения свободного падения и вектор полного ускорения
185 sagl::vec g = sagl::vec(0, -9.8, 0), a;
186 // Размер комнаты
187 double Size = 120;
188
189 // Изменение вектора скорости
190 V.Z = V.Z * exp(-n / m * Ani.DeltaTime);
191 V.Y = (V.Y - g.Y * m / n) * exp(-n / m * Ani.DeltaTime) + g.Y * m / n;
192 // Изменение вектора перемещения
193 P += V * Ani.DeltaTime;
194
195 // Ограничения - стенки
196 if (P.X > Size / 4)
197 V.X = -fabs(V.X);
198 if (P.X < -Size / 4)
199 V.X = fabs(V.X);
200
201 if (P.Y > Size / 4)
202 V.Y = -fabs(V.Y);
203 if (P.Y < -Size / 4)
204 V.Y = fabs(V.Y);
205
206 if (P.Z > Size / 4)
207 V.Z = -fabs(V.Z);
208 if (P.Z < -Size / 4)
209 V.Z = fabs(V.Z);
210
211 // Запоминание состояния изменения текущей СК
212 glPushMatrix();
213
214 // Рисование стенок
215 glutWireCube(Size / 2);
216 // Задача перемещения мяча
217 glTranslated(P.X, P.Y, P.Z);
218 // Цвет мяча
219 glColor3d(0, 1, 1);
220 // Рисование мяча
221 glutSolidSphere(0.5, 30, 30);
222
223 // Восстановление последнего запоминания состояния изменения текущей СК
224 glPopMatrix();
225 }
226 }; // end of 'ball_air_2' class
227
228 // Шар, летящий с сопротивлением воздуха
229 // Координаты получены методом Верле при линейной зависимости силы сопротивлении воздуха от скорости
230 class ball_air_3 : public sagl::object
231 {
232 private:
233 double angle, v, m, n;
234 public:
235 // Конструктор
236 ball_air_3( void ) : angle(Pi / 3), v(1), m(1), n(0.1)
237 {
238 P = sagl::vec(sagl::r0() + 5, 5, 0);
239 V.X = 0;
240 V.Y = sin(angle) * v;
241 V.Z = cos(angle) * v;
242 }
243
244 // Конструктор
245 ball_air_3( double angle1, double v1, double m1, double n1 ) : angle(angle1), v(v1), m(m1), n(n1)
246 {
247 P = sagl::vec(sagl::r0() + 5, 5, 0);
248 V.X = 0;
249 V.Y = sin(angle) * v;
250 V.Z = cos(angle) * v;
251 }
252
253 // Отрисовка объекта
254 void Render( sagl::anim &Ani )
255 {
256 // Вектор ускорения свободного падения и вектор полного ускорения
257 sagl::vec g = sagl::vec(0, -9.8, 0), a;
258 // Размер комнаты
259 double Size = 120;
260
261 // Изменение вектора ускорения
262 a = sagl::vec(0, g.Y - n / m * V.Y, -n / m * V.Z);
263
264 // Изменение вектора скорости
265 V += a * Ani.DeltaTime;
266 // Изменение вектора перемещения
267 P += V * Ani.DeltaTime;
268
269 // Ограничения - стенки
270 if (P.X > Size / 4)
271 V.X = -fabs(V.X);
272 if (P.X < -Size / 4)
273 V.X = fabs(V.X);
274
275 if (P.Y > Size / 4)
276 V.Y = -fabs(V.Y);
277 if (P.Y < -Size / 4)
278 V.Y = fabs(V.Y);
279
280 if (P.Z > Size / 4)
281 V.Z = -fabs(V.Z);
282 if (P.Z < -Size / 4)
283 V.Z = fabs(V.Z);
284
285 // Запоминание состояния изменения текущей СК
286 glPushMatrix();
287
288 // Рисование стенок
289 glutWireCube(Size / 2);
290 // Задача перемещения мяча
291 glTranslated(P.X, P.Y, P.Z);
292 // Цвет мяча
293 glColor3d(1, 0.5, 0);
294 // Рисование мяча
295 glutSolidSphere(0.5, 30, 30);
296
297 // Восстановление последнего запоминания состояния изменения текущей СК
298 glPopMatrix();
299 }
300 }; // end of 'ball_air_3' class
301
302 #endif /*__SAMPLE_H_ */
303
304 // END OF 'SAMPLE.H' FILE
Описание программы: программа состоит из четырех независимых друг от друга частей:
- Полет тела без сопротивления воздуха;
- Полет тела при линейной зависимости силы сопротивления воздуха от скорости, при котором координаты тела рассчитываются точным методом;
- Полет тела при линейной зависимости силы сопротивления воздуха от скорости, при котором координаты тела рассчитываются методом Верле;
- Полет тела при квадратичной зависимости силы сопротивлении воздуха от скорости, при котором координаты тела рассчитываются методом Верле;
Скачать можно тут.
1 // Первый случай
2
3 #include <iostream>
4 #include <math.h>
5 #include <cstdlib>
6 #include <fstream>
7
8 /// Программа, анализирующая полет тела;
9
10 using namespace std;
11 double a,s,H,p1,p2,X,f; /// Создание переменных, необходимых для работы:
12 /// a - угол к горизонту, под которым летит тело, вводится пользователем;
13 /// s - начальная скорость, с которой тело начинает лететь, вводится пользователем;
14 /// H - координата тела по оси Oy;
15 /// p1, p2 - промежуточные переменные, предназначенные для расчетов;
16 /// X - координата тела по оси Oy;
17 /// f - шаг по времени;
18
19 int main()
20 {
21 cout << "Enter speed and angle and step of time" << endl; /// Обращение к пользователю, где требуется ввести скорость тела, угол к горизонту и шаг по времени;
22 cin >> s >> a >> f; /// Считывание данных, введенных пользователем, в переменные;
23 double t=s*sin(a*3.14159/180.0)/9.8; /// Создание новой переменной t, хранящей значение времени полета тела вверх (вычисленное через уравнение скорости по оси Oy);
24 for (double i=f; i<(2*t+f); i+=f) /// Для вычисления координат тела в n-ом количестве точек мы создаем цикл, который повторяется то количество раз, сколько раз шаг по времени, введенным пользователем, вмещается во время полета всего тела;
25 {
26 p1=s*sin(a*3.14159/180)*i; /// Вычисление первой компоненты координаты тела по оси Oy, представляемй как произведение скорости по этой оси на время (выражено из уравнения равноускоренного прямолинейного движения);
27 p2=4.9*i*i; /// Вычисление второй компоненты координаты тела по оси Oy, представляемой как произведение квадрата времени на половину укорения свободного падения (выражено из уравнения РУПД);
28 H=double(p1)-p2; /// Вычисление координаты тела по оси Oy;
29 X=s*cos(a*3.14159/180)*i; /// Вычисление координаты тела по оси Ox как произведение скорости по оси Ox на время (выражено из уравнения равномерного движения);
30 cerr << X << " "; /// Вывод на экран значения по оси Ox
31 cerr << H << endl; /// и по оси Oy;
32 }
33 ofstream out("zap.txt"); /// Так как результаты анализа не только выводятся на экран, но и записываются в файл, мы создаем переменную, соответствующую файлу "Res.txt", находящемуся в папке с программой, и открываем файл для записи;
34 for (double i=0; i<(2*t+f); i+=f) /// Для вычисления координат тела в n-ом количестве точек мы создаем цикл, который повторяется то количество раз, сколько раз шаг по времени, введенным пользователем, вмещается во время полета всего тела;
35 {
36 p1=s*sin(a*3.14159/180)*i; /// Вычисление первой компоненты координаты тела по оси Oy, представляемй как произведение скорости по этой оси на время (выражено из уравнения равноускоренного прямолинейного движения);
37 p2=4.9*i*i; /// Вычисление второй компоненты координаты тела по оси Oy, представляемой как произведение квадрата времени на половину укорения свободного падения (выражено из уравнения РУПД);
38 H=double(p1)-p2; /// Вычисление координаты тела по оси Oy;
39 X=s*cos(a*3.14159/180)*i; /// Вычисление координаты тела по оси Ox как произведение скорости по оси Ox на время (выражено из уравнения равномерного движения);
40 out << X << " "; /// Запись в файл значения по оси Ox
41 out << H << endl; /// и по оси Oy;
42 }
43 out.close(); /// Закрываем файл, с которым работали в течение программы;
44 return 0; /// По умолчанию возвращаем функции int main значение 0, тем самым завершая программу;
45 }
46
47 // Второй случай
48
49 #include <iostream>
50 #include <math.h>
51 #include <cstdlib>
52 #include <fstream>
53
54 /// Программа, позволяющая описать полет точки при помощи точного метода;
55
56 using namespace std;
57 double v,a,st,m; /// Создание переменных, необходимых для работы:
58 /// v - модуль скорости, который задает сам пользователь;
59 /// a - угол относительно горизонта, под которым летит тело, задается пользователем;
60 /// st - шаг по времени, через который расчитываются координаты точек, задается пользователем;
61 /// m - масса тела, задается пользователем;
62 double *V,*X, *Y, *U; /// Создание массивов, хранящих значения типа double, в которых хранятся значения:
63 /// V - массив, хранящий значения скорости по оси Ox;
64 /// X - массив, хранящий координаты точки по оси Ox;
65 /// Y - массив, хранящий значения скорости по оси Oy;
66 /// U - массив, хранящий координаты точки по оси Oy;
67
68 int main()
69 {
70 cout << "Enter speed and angle and step of time and weight" << endl; /// Обращение к пользователю, где требуется ввести скорость тела, угол к горизонту, шаг по времени и массу тела;
71 cin >> v >> a >> st >> m; /// Считывание данных, введенных пользователей в переменные;
72 double t=(v/9.8)*sin(3.14159*a/180.0); /// Создание новой переменной t, хранящей значение времени всего полета тела, вычисленного, как два времени взлета (через уравнение скорости по оси Oy);
73 int n=2*t/st; /// Создание новой целочисленной переменной, которая равна времени полета тела (преобразование типов для переменной t) деленного на шаг, которая будет использоваться при создании массивов для размера;
74 //int p=1/st;
75 V = new double [n+2]; /// Создание динамического массива V, предназначенного для хранения значений скорости по оси Ox, размером (n+2) (n показывает, сколько раз шаг по времени помещается во все время, то есть, сколько точек мы будем рассматривать, анализируя полет точки);
76 X = new double [n+2]; /// Создание динамического массива X, предназначенного для хранения координаты тела по оси Ox и имеющего схожие характеристики с массивом V;
77 Y = new double [n+2]; /// Создание динамического массива X, предназначенного для хранения координаты тела по оси Oy и имеющего схожие характеристики с массивом V;
78 U = new double [n+2]; /// Создание динамического массива U, предназначенного для хранения значений скорости тела по оси Oy и имеющего схожие характеристики с массивом V;
79 V[0]=v*cos(3.14159*a/180.0); /// Вычисление значения скорости по оси Ox в начальный момент времени, как состовляющая модуля скорости, заданного пользователем;
80 X[0]=0; /// Задание координаты точки по оси Ox в начальный момент времени. Мы рассматриваем движение тела под углом к горизонту из начала координат, поэтому x=0;
81 U[0]=v*sin(3.14159*a/180.0); /// Вычисление значения скорости по оси Oy в начальный момент времени, как компонента модуля скорости, заданного пользователем, по вертикальной оси;
82 Y[0]=0; /// Задание координаты точки по оси Oy в начальный момент времени. Мы рассматриваем движение тела под углом к горизонту из начала координат, поэтому y=0;
83 ofstream out("Res.txt"); /// Так как результаты анализа не только выводятся на экран, но и записываются в файл, мы создаем переменную, соответствующую файлу "Res.txt", находящемуся в папке с программой, и открываем файл для записи;
84 for (int i=1; i<n; ++i) /// Для вычисления координат тела в пространстве в зависимости от времени мы создаем цикл, который позволяет, использая общую формулу нахождкения координат и компонент скорости, вычислять эти значения
85 /// Цикл повторяется (n-1) раз, так как значения в начальный момент времени были найдены отдельно от цикла, и повторяется столько раз, сколько точек траектории мы рассматриваем;
86 {
87 Y[i]=(m/0.001)*(U[0]+9.8*(m/0.001))*(1-exp(((0-0.001)/m)*i*st))-9.8*(m/0.001)*i*st; /// Вычисление координаты тела в момент времени (i*st) по оси Oy по формуле, выведенной через дифференциальное уравнение точки для вертикальной оси и находящей координату как функцию от времени и координаты тела в предыдущей рассматриваемой нами точке;
88 X[i]=V[0]*(m/0.001)*(1-exp(((0-0.001)/m)*i*st)); /// Аналогично вычисляем координаты тела в момент времени (i*st) по оси Ox как функцию от времени и координате в предыдущей рассматриваемой точке;
89 /// В приведенных выше формулах зачение 0.001 - это коэффициент сопротивления воздуха;
90 /// Движение по горизонтальной оси рассматривается как равномерное прямолинейное движение;
91 /// Движение по вертикальной оси рассматривается как равноускоренное прямолинейное движение;
92 cerr << X[i] << " " << Y[i] << endl; /// Выведение рассчитанных значений на экран в виде строки, где первым идет координата по оси Ox, вторым - по оси Oy;
93 out << X[i] << " " << Y[i] << endl; /// Запись рассчитанных значений в файл "Res.txt" в виде строки, где первым идет координата по оси Ox, вторым - по оси Oy;
94 /// Таким образом, в результате работы программы мы получаем два столбика значений для координат по обеим осям, которые как записаны в файл, так и выведены на экран;
95 }
96 out.close(); /// Закрываем файл, с которым работали в течение программы;
97 return 0; /// По умолчанию возвращаем функции int main значение 0, тем самым завершая программу;
98
99
100 }
101
102 // Третий случай
103
104 #include <iostream>
105 #include <math.h>
106 #include <cstdlib>
107 #include <fstream>
108
109 /// Программа, анализирующая полет тела при помощи модифицированного метода Верле;
110
111 using namespace std;
112 double v,a,st,m,x,y; /// Создание переменных, необходимых для работы;
113 /// v - модуль скорости, который задает сам пользователь;
114 /// a - угол относительно горизонта, под которым летит тело, задается пользователем;
115 /// st - шаг по времени, через который расчитываются координаты точек, задается пользователем;
116 /// m - масса тела, задается пользователем;
117 /// x - координата тела по оси Ox в мнимый момент времени t=-1;
118 /// y - координата тела по оси Oy в мнимый момент времени t=-1;
119 double *V,*X, *Y, *U; /// Создание массивов, хранящих значения типа double, в которых хранятся значения:
120 /// V - массив, хранящий значения скорости по оси Ox;
121 /// X - массив, хранящий координаты точки по оси Ox;
122 /// Y - массив, хранящий значения скорости по оси Oy;
123 /// U - массив, хранящий координаты точки по оси Oy;
124
125 int main()
126 {
127 cout << "Enter speed and angle and step of time and weight" << endl; /// Обращение к пользователю, где требуется ввести скорость тела, угол к горизонту, шаг по времени и массу тела;
128 cin >> v >> a >> st >> m; /// Считывание данных, введенных пользователей в переменные;
129 double t=(v/9.8)*sin(3.14159*a/180.0); /// Создание новой переменной t, хранящей значение времени всего полета тела, вычисленного, как два времени взлета (через уравнение скорости по оси Oy);
130 int n=2*t/st; /// Создание новой целочисленной переменной, которая равна времени полета тела (преобразование типов для переменной t) деленного на шаг, которая будет использоваться при создании массивов для размера;
131 //int p=1/st;
132 V = new double [n+2]; /// Создание динамического массива V, предназначенного для хранения значений скорости по оси Ox, размером (n+2) (n показывает, сколько раз шаг по времени помещается во все время, то есть, сколько точек мы будем рассматривать, анализируя полет точки);
133 X = new double [n+2]; /// Создание динамического массива X, предназначенного для хранения координаты тела по оси Ox и имеющего схожие характеристики с массивом V;
134 Y = new double [n+2]; /// Создание динамического массива X, предназначенного для хранения координаты тела по оси Oy и имеющего схожие характеристики с массивом V;
135 U = new double [n+2]; /// Создание динамического массива U, предназначенного для хранения значений скорости тела по оси Oy и имеющего схожие характеристики с массивом V;
136 V[0]=v*cos(3.14159*a/180.0); /// Вычисление значения скорости по оси Ox в начальный момент времени, как состовляющая модуля скорости, заданного пользователем;
137 X[0]=0; /// Задание координаты точки по оси Ox в начальный момент времени. Мы рассматриваем движение тела под углом к горизонту из начала координат, поэтому x=0;
138 x=X[0]-V[0]*st; /// Суть данного метода заключается в том, что мы находим значение параметров тела по предыдущим двум состояниям, поэтому нам нужно вычислить мнимые координаты тела в -1 момент времени. Это расчет коордлинаты по оси Ox;
139 X[1]=2*X[0]-x-(0.01/m)*V[0]*st*st; /// Вычисление координаты тела по оси Ox в момент времени t=1;
140 U[0]=v*sin(3.14159*a/180.0); /// Вычисление значения скорости по оси Oy в начальный момент времени, как компонента модуля скорости, заданного пользователем, по вертикальной оси;
141 Y[0]=0; /// Задание координаты точки по оси Oy в начальный момент времени. Мы рассматриваем движение тела под углом к горизонту из начала координат, поэтому y=0;
142 y=Y[0]-U[0]*st; /// Суть данного метода заключается в том, что мы находим значение параметров тела по предыдущим двум состояниям, поэтому нам нужно вычислить мнимые координаты тела в -1 момент времени. Это расчет коордлинаты по оси Oу;
143 Y[1]=2*Y[0]-y-(0.01/m)*U[0]*st*st; /// Вычисление координаты тела по оси Oу в момент времени t=1;
144 cerr << X[1] << " " << Y[1] << endl; /// Вывод на экран значений координат по обеим осям в момент времени t=1;
145 ofstream out("Res.txt"); /// Так как результаты анализа не только выводятся на экран, но и записываются в файл, мы создаем переменную, соответствующую файлу "Res.txt", находящемуся в папке с программой, и открываем файл для записи;
146 out << X[1] << " " << Y[1] << endl; /// Записываем в файл полученные значения координат тела в момент времени t=1;
147 int k=1; /// Создаем целочисленную переменную k=1 для работы в цикле;
148 //cerr<<"N "<<n<<"\n";
149 for (int i=0; i<n; ++i) /// Для вычисления координат тела в пространстве в зависимости от времени мы создаем цикл, который позволяет, использая общую формулу нахождкения координат и компонент скорости, вычислять эти значения
150 /// Цикл повторяется (n-1) раз, так как значения в начальный момент времени были найдены отдельно от цикла, и повторяется столько раз, сколько точек траектории мы рассматриваем;
151 {
152 X[k+1]=2.0*X[k]-X[k-1]-(0.001/m)*V[k]*st*st; /// Нахождение координаты тела по оси Ox в момент времени t, основываясь на известных параметрах за моменты времени t-1 и t-2;
153 V[k]=(X[k+1]-X[k-1])/(2*st); /// Нахождение значения скорости тела по оси Ox в момент времени t-1, основываясь на рассчитанных выше координатах тела по оси Ox длямоментов времени t и t-2;
154 Y[k+1]=2.0*Y[k]-Y[k-1]-(9.8+(0.001/m)*U[k])*st*st; /// Нахождение координаты тела по оси Oy в момент времени t, основываясь на известных параметрах за моменты времени t-1 и t-2;
155 U[k]=(Y[k+1]-Y[k-1])/(2*st); /// Нахождение значения скорости тела по оси Oy в момент времени t-1, основываясь на рассчитанных выше координатах тела по оси Ox длямоментов времени t и t-2;
156 //cerr <<i<<" "<<k<<" "<<
157 cerr << X[k+1] << " " << Y[k+1] << endl; /// Выведение рассчитанных значений на экран в виде строки, где первым идет координата по оси Ox, вторым - по оси Oy;
158 out << X[k+1] << " " << Y[k+1] << endl; /// Запись рассчитанных значений в файл "Res.txt" в виде строки, где первым идет координата по оси Ox, вторым - по оси Oy;
159 k=k+1; /// Увеличиваем число k на единицу, чтобы в следующем шаге цикла рассчитать значения для следующего момента времени;
160 /// Таким образом, в результате работы программы мы получаем два столбика значений для координат по обеим осям, которые как записаны в файл, так и выведены на экран;
161 }
162 out.close(); /// Закрываем файл, с которым работали в течение программы;
163 return 0; /// По умолчанию возвращаем функции int main значение 0, тем самым завершая программу;
164 }
165
166 // Четвертый случай
167
168 #include <iostream>
169 #include <math.h>
170 #include <cstdlib>
171 #include <fstream>
172
173 /// Программа, анализирующая полет тела при помощи метода Верле;
174
175 using namespace std;
176 double v,a,st,m,x,y; /// Создание переменных, необходимых для работы:
177 /// v - модуль скорости, который задает сам пользователь;
178 /// a - угол относительно горизонта, под которым летит тело, задается пользователем;
179 /// st - шаг по времени, через который расчитываются координаты точек, задается пользователем;
180 /// m - масса тела, задается пользователем;
181 /// x - координата тела по оси Ox в мнимый момент времени t=-1;
182 /// y - координата тела по оси Oy в мнимый момент времени t=-1;
183 double *V,*X, *Y, *U; /// Создание массивов, хранящих значения типа double, в которых хранятся значения:
184 /// V - массив, хранящий значения скорости по оси Ox;
185 /// X - массив, хранящий координаты точки по оси Ox;
186 /// Y - массив, хранящий значения скорости по оси Oy;
187 /// U - массив, хранящий координаты точки по оси Oy;
188
189 int main()
190 {
191 cout << "Enter speed and angle and step of time and weight" << endl; /// Обращение к пользователю, где требуется ввести скорость тела, угол к горизонту, шаг по времени и массу тела;
192 cin >> v >> a >> st >> m; /// Считывание данных, введенных пользователем, в переменные;
193 double t=(v/9.8)*sin(3.14159*a/180.0); /// Создание новой переменной t, хранящей значение времени всего полета тела, вычисленного, как два времени взлета (через уравнение скорости по оси Oy);
194 int n=2*t/st; /// Создание новой целочисленной переменной, которая равна времени полета тела (преобразование типов для переменной t) деленного на шаг, которая будет использоваться при создании массивов для размера;
195 //int p=1/st;
196 V = new double [n+2]; /// Создание динамического массива V, предназначенного для хранения значений скорости по оси Ox, размером (n+2) (n показывает, сколько раз шаг по времени помещается во все время, то есть, сколько точек мы будем рассматривать, анализируя полет точки);
197 X = new double [n+2]; /// Создание динамического массива X, предназначенного для хранения координаты тела по оси Ox и имеющего схожие характеристики с массивом V;
198 Y = new double [n+2]; /// Создание динамического массива X, предназначенного для хранения координаты тела по оси Oy и имеющего схожие характеристики с массивом V;
199 U = new double [n+2]; /// Создание динамического массива U, предназначенного для хранения значений скорости тела по оси Oy и имеющего схожие характеристики с массивом V;
200 V[0]=v*cos(3.14159*a/180.0); /// Вычисление значения скорости по оси Ox в начальный момент времени, как состовляющая модуля скорости, заданного пользователем;
201 X[0]=0; /// Задание координаты точки по оси Ox в начальный момент времени. Мы рассматриваем движение тела под углом к горизонту из начала координат, поэтому x=0;
202 x=X[0]-V[0]*st; /// Суть данного метода заключается в том, что мы находим значение параметров тела по предыдущим двум состояниям, поэтому нам нужно вычислить мнимые координаты тела в -1 момент времени. Это расчет коордлинаты по оси Ox;
203 X[1]=2*X[0]-x-(0.01/m)*V[0]*V[0]/cos(3.14159*a/180.0)*st*st; /// Вычисление координаты тела по оси Ox в момент времени t=1;
204 U[0]=v*sin(3.14159*a/180.0); /// Вычисление значения скорости по оси Oy в начальный момент времени, как компонента модуля скорости, заданного пользователем, по вертикальной оси;
205 Y[0]=0; /// Задание координаты точки по оси Oy в начальный момент времени. Мы рассматриваем движение тела под углом к горизонту из начала координат, поэтому y=0;
206 y=Y[0]-U[0]*st; /// Суть данного метода заключается в том, что мы находим значение параметров тела по предыдущим двум состояниям, поэтому нам нужно вычислить мнимые координаты тела в -1 момент времени. Это расчет коордлинаты по оси Oу;
207 Y[1]=2*Y[0]-y-(0.01/m)*U[0]*U[0]/sin(3.14159*a/180.0)*st*st; /// Вычисление координаты тела по оси Oу в момент времени t=1;
208 cerr << X[1] << " " << Y[1] << endl; /// Вывод на экран значений координат по обеим осям в момент времени t=1;
209 ofstream out("Res.txt"); /// Так как результаты анализа не только выводятся на экран, но и записываются в файл, мы создаем переменную, соответствующую файлу "Res.txt", находящемуся в папке с программой, и открываем файл для записи;
210 out << X[1] << " " << Y[1] << endl; /// Записываем в файл полученные значения координат тела в момент времени t=1;
211 int k=1; /// Создаем целочисленную переменную k=1 для работы в цикле;
212 //cerr<<"N "<<n<<"\n";
213 for (int i=0; i<n; ++i) /// Для вычисления координат тела в пространстве в зависимости от времени мы создаем цикл, который позволяет, использая общую формулу нахождкения координат и компонент скорости, вычислять эти значения
214 /// Цикл повторяется (n-1) раз, так как значения в начальный момент времени были найдены отдельно от цикла, и повторяется столько раз, сколько точек траектории мы рассматриваем;
215 {
216 X[k+1]=2.0*X[k]-X[k-1]-(0.001/m)*V[k]*V[k]*st*st; /// Нахождение координаты тела по оси Ox в момент времени t, основываясь на известных параметрах за моменты времени t-1 и t-2;
217 V[k]=(X[k+1]-X[k-1])/(2*st); /// Нахождение значения скорости тела по оси Ox в момент времени t-1, основываясь на рассчитанных выше координатах тела по оси Ox длямоментов времени t и t-2;
218 Y[k+1]=2.0*Y[k]-Y[k-1]-(9.8+(0.001/m)*U[k]*U[k])*st*st; /// Нахождение координаты тела по оси Oy в момент времени t, основываясь на известных параметрах за моменты времени t-1 и t-2;
219 U[k]=(Y[k+1]-Y[k-1])/(2*st); /// Нахождение значения скорости тела по оси Oy в момент времени t-1, основываясь на рассчитанных выше координатах тела по оси Ox длямоментов времени t и t-2;
220 //cerr <<i<<" "<<k<<" "<<
221 cerr << X[k+1] << " " << Y[k+1] << endl; /// Выведение рассчитанных значений на экран в виде строки, где первым идет координата по оси Ox, вторым - по оси Oy;
222 out << X[k+1] << " " << Y[k+1] << endl; /// Запись рассчитанных значений в файл "Res.txt" в виде строки, где первым идет координата по оси Ox, вторым - по оси Oy;
223 k=k+1; /// Увеличиваем число k на единицу, чтобы в следующем шаге цикла рассчитать значения для следующего момента времени;
224 /// Таким образом, в результате работы программы мы получаем два столбика значений для координат по обеим осям, которые как записаны в файл, так и выведены на экран;
225 }
226 out.close(); /// Закрываем файл, с которым работали в течение программы;
227 return 0; /// По умолчанию возвращаем функции int main значение 0, тем самым завершая программу;
228 }
Описание: Пользователя попросят ввести начальную скорость, угол бросания, тогда программа запишет в файл результаты следующих вычислений:
- Координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
- Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости;
- Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости.
- Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости;
1 #include <stdio.h>
2 #include <stdlib.h>
3 #include <cmath>
4
5 using namespace std;
6
7 FILE *output;
8
9 double e = 0.0000001; //точность
10 double g = 9.8; //ускорение свободного падения
11 double dt = 0.00001; //шаг по времени
12 double windageLinearCoefficient = 0.1;
13 double windageSquareCoefficient = 0.00001;
14
15 struct Vector //вектор
16 {
17 double x, y;
18 Vector():x(0), y(0)
19 {}
20 Vector(double x, double y):x(x), y(y)
21 {}
22 const Vector operator+(const Vector &v) const
23 {
24 return Vector(this -> x + v.x, this -> y + v.y);
25 }
26 const Vector operator-(const Vector &v) const
27 {
28 return Vector(this -> x - v.x, this -> y - v.y);
29 }
30 const Vector operator*(const double k) const
31 {
32 return Vector(this -> x * k, this -> y * k);
33 }
34 const Vector operator*(const int k) const
35 {
36 return Vector(this -> x * k, this -> y * k);
37 }
38 const Vector operator/(const double k) const
39 {
40 return Vector(this -> x / k, this -> y / k);
41 }
42 };
43
44 const Vector operator*(const double a, const Vector &v)
45 {
46 return Vector(v.x * a, v.y * a);
47 }
48
49 const Vector operator*(const int k, const Vector &v)
50 {
51 return Vector(v.x * k, v.y * k);
52 }
53
54 double abs(const Vector &v)
55 {
56 return sqrt(v.x * v.x + v.y * v.y);
57 }
58
59 void printCoordinate(const char *description, const Vector &v) //выводит координаты в более читаемом виде
60 {
61 fputs(description, output);
62 fputs(": ", output);
63 fprintf(output, "%lf", v.x);
64 fputs(", ", output);
65 fprintf(output, "%lf\n", v.y);
66 }
67
68 Vector getCoordinatesWithoutWindage(double velocity, double angle, double time = -1)
69 {
70 double fallTime = 2 * velocity * sin(angle) / g; //расчет времени падения
71 if((time < 0) or (time > fallTime))
72 time = fallTime;
73 double x = velocity * cos(angle) * time; // x = vx*t;
74 double y = velocity * sin(angle) * time - g * time * time / 2; // y = vy*t-(g*t^2)/2;
75 return Vector(x, y);
76 }
77
78 Vector getCoordinatesVerletLinear(double velocity, double angle, double time = -1)
79 {
80 double nowTime = dt;
81 Vector rsb(0, 0);
82 if((time >= 0) and (dt / 2 - time > 0)) //если время расчета дается слишком малого промежутка
83 return rsb; //вернитесь в начальную точку
84 Vector v(velocity * cos(angle), velocity * sin(angle)); //проекции начальной скорости
85 Vector r = v * dt; //вторая точка
86 Vector a = -windageLinearCoefficient * v; //ускорение в начальной точке
87 a.y -= g;
88 v = v + a * dt; //скорость во второй точке
89 a = -windageLinearCoefficient * v; //ускорение во второй точке
90 a.y -= g;
91 while((r.y > 0) or ((time > 0) and (nowTime <= time))) //пока точка выше 0 или не достигла заданного времени
92 {
93 Vector rn = 2 * r - rsb + a * dt * dt; // r(t+dt) = 2*r(t)-r(t-dt)+a(t)*dt^2;
94 v = (rn - rsb) / (2 * dt); // v(t) = (r(t+dt)-r(t-dt))/(2*dt);
95 rsb = r; //обновление r(t-dt) and r(t)
96 r = rn;
97 a = -windageLinearCoefficient * v; //обновление a(t)
98 a.y -= g;
99 nowTime += dt; //обновленное время
100 }
101 return r;
102 }
103
104 Vector calculateForTime(Vector &v, double time)
105 {
106 Vector r;
107 // x = vx/k*(1-e^(-k*t));
108 r.x = v.x / windageLinearCoefficient * (1 - exp(-windageLinearCoefficient * time));
109 // y = ((vy+g/k)*(1-e^(-k*t))-g*t)/k;
110 r.y = ((v.y + g / windageLinearCoefficient) * (1 - exp(-windageLinearCoefficient * time)) - g * time) / windageLinearCoefficient;
111 return r;
112 }
113
114 Vector getCoordinatesAccurateLinear(double velocity, double angle, double time = -1)
115 {
116 if(windageLinearCoefficient < e) //если коэффициент слишком близок к нулю
117 return getCoordinatesWithoutWindage(velocity, angle, time); //вычисляй будто это 0
118 Vector r;
119 Vector v(velocity * cos(angle), velocity * sin(angle)); //проекции начальной скорости
120 if(time >= 0) //время данное
121 {
122 r = calculateForTime(v, time);
123 if(r.y >= 0) //если объект в воздухе или только приземлился
124 return r; //затем верните координаты объекта
125 else //еще
126 return getCoordinatesAccurateLinear(velocity, angle); //верните координаты приземления
127 }
128 else
129 {
130 double timer, timel, timem;
131 timer = v.y / g;
132 timel = 0;
133 while(calculateForTime(v, timer).y > 0) //смотрим на некоторые значения времени, которые больше времени посадки
134 timer *= 1.5;
135 timem = timel + (timer - timel) / 2;
136 r = calculateForTime(v, timem);
137 while(abs(r.y) > e) //бинарный поиск времени посадки
138 {
139 if(r.y > 0)
140 timel = timem;
141 else
142 timer = timem;
143 timem = timel + (timer - timel) / 2;
144 r = calculateForTime(v, timem);
145 }
146 return r;
147 }
148 }
149
150 Vector getCoordinatesVerletSquare(double velocity, double angle, double time = -1)
151 {
152 double nowTime = dt;
153 Vector rsb(0, 0);
154 if((dt / 2 - time > 0)and(time >= 0)) //если время слишком малое для рсчета
155 return rsb; //вернитесь в начальную точку
156 Vector v(velocity * cos(angle), velocity * sin(angle)); //проекции начальной скорости
157 Vector r = v * dt; //вторая точка
158 Vector a = -abs(v) * v * windageSquareCoefficient; //ускорение в начальной точке
159 a.y -= g;
160 v = v + a * dt; //скорость во второй точке
161 a = -abs(v) * v * windageSquareCoefficient; //ускорение во второй точке
162 a.y -= g;
163 while((r.y > 0) or ((time > 0) and (nowTime <= time))) //когда точка выше нулевой отметки и не достигает заданного времени
164 {
165 Vector rn = 2 * r - rsb + a * dt * dt; // r(t+dt) = 2*r(t)-r(t-dt)+a(t)*dt^2;
166 v = (rn - rsb) / (2 * dt); // v(t) = (r(t+dt)-r(t-dt))/(2*dt);
167 rsb = r; //updating r(t-dt) and r(t)
168 r = rn;
169 a = -abs(v) * v * windageSquareCoefficient; //новое a(t)
170 a.y -= g;
171 nowTime += dt; //новое a(t)
172 }
173 return r;
174 }
175
176 void err(const char *s) //печатает сообщение об ошибке и завершает работу
177 {
178 fputs(s, output);
179 exit(1);
180 }
181
182 int main(int argc, const char *argv[])
183 {
184 double velocity, angle;
185 bool needRead = true;
186 if(argc==3) //если даны 2 аргумента
187 {
188 velocity = atof(argv[1]); //истолкование его как скорости и угла
189 angle = atof(argv[2]);
190 needRead = false;
191 }
192 if(needRead)
193 {
194 puts("Enter initial velocity (m/s)");
195 scanf("%lf", &velocity);
196 }
197 if(velocity < 0) //проверка, если скорость меньше 0
198 err("Initial velocity must be above 0");
199 if(needRead)
200 {
201 puts("Enter initial angle (0-180 degrees)");
202 scanf("%lf", &angle);
203 }
204 if((angle < 0) or (angle > 180)) //проверка, что угол в нужном интервале
205 err("Initial angle must be from 0 to 180");
206 angle = angle / 180 * M_PI; // a = a/180*pi; преобразование угла из градусов в радианы
207 output = fopen("Coordinates.txt", "w"); //открытие результативного файла
208 //вычисление и печать 4 значений
209 printCoordinate("Without windage", getCoordinatesWithoutWindage(velocity, angle));
210 printCoordinate("Verlet, linear dependence", getCoordinatesVerletLinear(velocity, angle));
211 printCoordinate("Accurate, linear dependence", getCoordinatesAccurateLinear(velocity, angle));
212 printCoordinate("Verlet, square dependence", getCoordinatesVerletSquare(velocity, angle));
213 fclose(output); //закрытие файла
214 return 0;
215 }
Скачать можно здесь
Суть программы:Программа позволяет отслеживать траекторию движения тела, брошенного под углом к горизонту, в каждом из четырех случаев/методов.
Идея: Программа состоит из четырех методов: 1) движение тела без учета сопротивления воздуха; 2) движение тела с учетом сопротивления воздуха по первому методу Верле; 3) движение тела с учетом сопротивления воздуха по точному методу; 4) движение тела с учетом сопротивления воздуха по второму методу Верле.
Инструкция: Результаты программы будут записаны в соответствующий файл (подробности смотри в самой программе). Пользователю будет предоставлена возможность ввести начальную скорость и угол, под которым и бросают тело.
Ссылка для скачиваний: здесь.
Описание программы: программа записывает в четыре файла результаты вычисления:
- Координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
- Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости;
- Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости;
- Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости.
Скачать можно тут.
Для тела с массой 1,сопротивлением воздуха 0.05, угол бросания 30°, начальная скорость 40 м/с, ускорение свободного падения 9.8 м/c^2;
Файл "main.cpp"
1 #include <iostream>
2 #include <locale.h>
3 #include <math.h>
4 #include <fstream>
5 #include<iomanip>
6 #include <cmath>
7 using namespace std;
8 main ()
9 {
10 ofstream F; //a1-угол в градусах,dt-шаг,r-сопротивление воздуха
11 int u0=50;
12 double x,y,t,a,a1=30,dt=0.1,y0=0,x0=0,g=9.8,r=0.05,m=1,ux,uy,ypr,xpr,ysl,xsl,u,yt; //ux,uy - проэкции скорости на оси х и у.
13 a=a1*M_PI/180; //Градусы в радианы
14 t=0;
15
16 //Движение без сопротивления воздуха
17 F.open("C:\\1.txt",ios::out);
18 while(y>=0)
19 {
20 x=x0+u0*cos(M_PI/6)*t;
21 y=y0+u0*sin(M_PI/6)*t - 0.5 * g * t * t; //Расчитываем координаты в каждой точке через шаг
22 F<<x<<" "<<y<<endl;
23 t=t+dt;
24
25 }
26
27 F.close();
28 //Точное решение для линейной зависимости
29 F.open("C:\\2.txt",ios::out);
30 y=y0;
31 x=x0;
32 t=0; //Расчитываем координаты в каждой точке через шаг
33 while(y>=0)
34 {
35 ux = u0 * cos(a);
36 uy = u0 * sin(a);
37 x = x0+ (m * ux / r)* (1 - exp(-1 * r * t / m)); //подстановка формул
38 y = y0+(m/r)*((uy + g * m / r)*(1 - exp(-1 * r * t / m)) - g * t);
39 t = t + dt;
40
41 F << x << ' ' << y << endl;
42
43
44
45 }
46 F.close();
47 //метод Верле 1
48 ypr = y0 - u0*sin(a)*dt;
49 yt=ypr;
50 xpr = x0 - u0*cos(a)*dt;
51 x = x0; //Начальные условия
52 y = y0;
53 u = u0;
54 ux = u0 * cos(a);
55 uy = u0 * sin(a);
56 F.open("C:\\3.txt",ios::out);
57
58 while (y >= y0)
59 {
60 xsl = 2 * x - xpr - (r / m) * u * ux * (dt * dt);
61 ux = ( xsl - xpr )/ (2 * dt);
62 ysl = 2 * y - ypr - (g + (r / m) * u * uy) * (dt * dt); //xsl,ysl - координаты на шаге вперед. xpr,ypr- назад
63 uy = (ysl - ypr)/ (2 * dt);
64 u = sqrt(uy*uy + ux*ux );
65 F << x << ' ' << y << endl;
66
67 xpr = x;
68 x = xsl;
69 ypr = y;
70 y = ysl;
71 }
72 F.close();
73 //Метод Верле 2
74 ypr = y0 - u0*sin(a)*dt;
75 yt=ypr;
76 xpr = x0 - u0*cos(a)*dt;
77 x = x0; //xsl,ysl - координаты на шаге вперед. xpr,ypr- назад
78 y = y0;
79 u = u0;
80 ux = u0 * cos(a);
81 uy = u0 * sin(a);
82 F.open("C:\\4.txt",ios::out);
83
84 while (y >= y0)
85 {
86 xsl = 2 * x - xpr - (r / m) * ux * (dt * dt);
87 ux = ( xsl - xpr )/ (2 * dt);
88 ysl = 2 * y - ypr - (g + (r / m) * uy) * (dt * dt);
89 uy = (ysl - ypr)/ (2 * dt);
90 u = sqrt(uy*uy + ux*ux );
91 F << x << ' ' << y << endl;
92
93 xpr = x;
94 x = xsl;
95 ypr = y;
96 y = ysl;
97 }
98 F.close();
99
100
101 return 0;
102
103
104 }
Описание программы: Программа записывает в текстовый файл результаты вычисления координат по x и y с шагом в 0.1 секунду(возможно изменить) четырьмя различными способами:
- Координаты, рассчитанные по формуле, при движении без сопротивления воздуха
- Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости
- Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости
- Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости
Скачать можно тут.
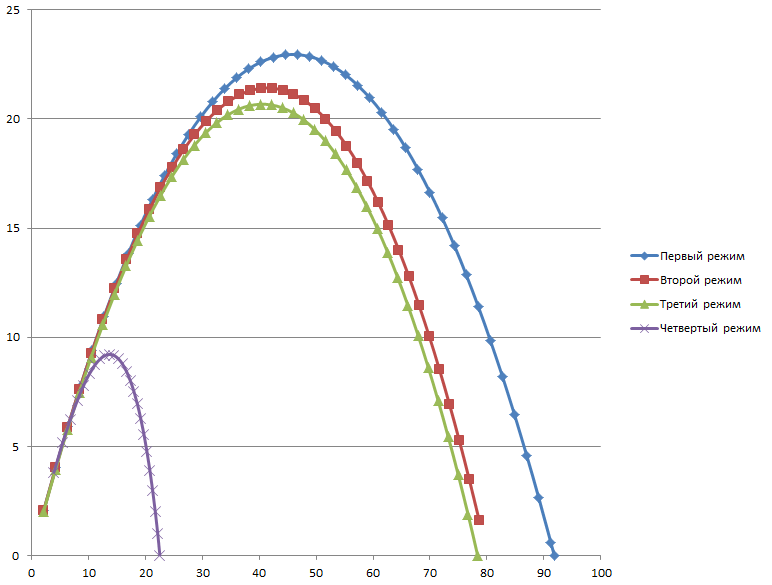
1 #include <iostream>
2 #include <fstream>
3 #include <math.h>
4 #include <cmath>
5 using namespace std;
6 int o;
7 double v,a,m,k;
8 ofstream fout("file.txt");//создаем объект, сяванный с файлом file.txt
9
10
11
12 int rez_1(double v, double a)
13 {
14 fout<<"---------------Первый режим-------------------------"<<endl;
15 fout<<" T=0 x=0 y=0";
16 fout<<endl;
17 double x=0,y=0,t=0.1, V0x, V0y, g=9.8,t1, T=0.1, Ty;
18 V0x=v*cos(a/180*M_PI);//рассчет проекций начальных скоростей на оси x и y с переводом угла в радианы
19 V0y=v*sin(a/180*M_PI);
20 Ty=2*V0y/g;//время полета
21 while (y>0 || x==0)//условие: пока тело не упадет на землю(те y=0, при этом не учитывая начало полета
22 {
23 x=x+V0x*t; //ф-лы для рассчета x и y в данный момент времени
24 y=y+V0y*t-g*pow(t,2)/2;
25
26 if (y<0) //если y<0
27 {
28 t1=Ty-T; //рассчитываем время,которое осталось лететь телу до земли
29 x=x+V0x*t1;//используя это время находим координату по х
30 fout<<" T="<<Ty<<" x="<<x<<" y=0"<<endl;//ввод в текстовый файл
31 break;
32 }
33 else
34 {
35 V0y=V0y-g*t;// иначе находим новую скорость по y (по x не меняется)
36 fout<<" T="<<T<<" x="<<x<<" y="<<y<<endl;
37 T=T+t;//увел время на шаг
38 }
39 }
40
41
42 }
43
44
45 int rez_2(double v, double a, double k, double m)
46 {
47 fout<<"---------------Второй режим работы-------------------------"<<endl;
48 fout<<" T=0 x=0 y=0";
49 fout<<endl;
50 double t=0.1, Vx=v*cos(a/180*M_PI), Vy=v*sin(a/180*M_PI),y,x,T=0.1,g=9.8;
51 x=(m*Vx/k)*(1-exp(-1*k*T/m)); //ф-лы для рассчета x и y в данный момент времени
52 y =(m/k)*((Vy+g*m/k)*(1-exp(-1*k*T/m))-g*T); //точное решение при лин завсисимости
53 while (y>0)
54 {
55 x=(m*Vx/k)*(1-exp(-1*k*T/m));
56 y =(m/k)*((Vy+g*m/k)*(1-exp(-1*k*T/m))-g*T);
57 fout<<" T="<<T<<" x="<<x<<" y="<<y<<endl;
58 T=T+t;
59 }
60
61
62 }
63
64
65
66 int rez_3(double v, double a, double k, double m)
67 {
68 fout<<"---------------Третий режим работы-------------------------"<<endl;
69 fout<<" T=0 x=0 y=0";
70 fout<<endl;
71 double t=0.1, Vxn=v*cos(a/180*M_PI), Vyn=v*sin(a/180*M_PI),
72 x3=0,x2=0,x1=x2-Vxn*t, y3=0,
73 y2=0, y1=y2-Vyn*t, g=9.8, t1, T=0.1;//шаг, скорость по х в момент времени T, -\\- по y в момент времени Т
74 //координата по х в в момент времени T, -\\- в n-1 шаг, -\\- в n шаге, аналогично для y,
75
76
77 x3=2*x2-x1-k/m*Vxn*pow(t,2); //координаты в момент времени T
78 y3=2*y2-y1-(g-+k/m*Vyn)*pow(t,2);
79 Vxn=(x3-x1)/(2.0*t); //скорость в момент времени T
80 Vyn=(y3-y1)/(2.0*t);
81 x1=x2;// приравнивание к координате на n-1 шаге значение координаты в n шаге
82 y1=y2;
83 x2=x3;//-//- к координате в n шаге значение в момент времени T
84 y2=y3;
85 while (y2>0)
86 {
87 x3=2*x2-x1-k/m*Vxn*pow(t,2);
88 y3=2*y2-y1-(g+k/m*Vyn)*pow(t,2);
89 Vxn=(x3-x1)/(2.0*t);
90 Vyn=(y3-y1)/(2.0*t);
91 fout<<" T="<<T<<" x="<<x2<<" y="<<y2<<endl;
92
93 if (y3<0)
94 {
95 t1=sqrt(abs((-y1+2*y2)/(g+k/m*Vyn)));
96 x3=2*x2-x1-k/m*Vxn*pow((t+t1),2);
97 fout<<" T="<<T+t1<<" x="<<x3<<" y="<<0<<endl;
98 }
99
100 T=T+t;
101 x1=x2;
102 y1=y2;
103 x2=x3;
104 y2=y3;
105
106 }
107
108 }
109
110
111 int rez_4(double v, double a, double k, double m)
112 {
113 fout<<"---------------Четвертый режим работы-------------------------"<<endl;
114 fout<<" T=0 x=0 y=0";
115 fout<<endl;
116 double t=0.1, Vxn=v*cos(a/180*M_PI), Vyn=v*sin(a/180*M_PI),
117 x3=0,x1=0, x2=x1+Vxn*t, y3=0, y1=0,
118 y2=y1+Vyn*t, g=9.8, t1, T=0.1, V=v;//шаг, скорость по х в момент времени T, -\\- по y в момент времени Т
119 //координата по х в в момент времени T, -\\- в n-1 шаг, -\\- в n шаге, аналогично для y,
120
121
122 x3=2.0*x2-x1-(k/m)*V*Vxn*pow(t,2);
123 y3=2.0*y2-y1-(g+(k/m)*V*Vyn)*pow(t,2);
124 Vxn=(x3-x1)/(2.0*t);
125 Vyn=(y3-y1)/(2.0*t);
126 V=sqrt(pow(Vxn,2)+pow(Vyn,2.0));
127 x1=x2;
128 y1=y2;
129 x2=x3;
130 y2=y3;
131 while (y2>0)
132 {
133 x3=2.0*x2-x1-(k/m)*Vxn*V*pow(t,2);
134 y3=2.0*y2-y1-(g+(k/m)*Vyn*V)*pow(t,2);
135 Vxn=(x3-x1)/(2.0*t);
136 Vyn=(y3-y1)/(2.0*t);
137 V=sqrt(pow(Vxn,2)+pow(Vyn,2));
138 fout<<" T="<<T<<" x="<<x2<<" y="<<y2<<endl;
139
140 if (y3<0)
141 {
142 t1=sqrt(abs((-y1+2.0*y2)/(g+(k/m)*Vyn*V)));
143 x3=2.0*x2-x1-(k/m)*Vxn*V*pow((t+t1),2);
144 fout<<" T="<<T+t1<<" x="<<x3<<" y="<<0<<endl;
145 }
146
147
148 T=T+t;
149 x1=x2;
150 y1=y2;
151 x2=x3;
152 y2=y3;
153
154 }
155
156 }
157
158
159 int main()
160 {
161
162 setlocale(LC_ALL, "rus");
163 cout<<"Введите скорость тела и угол"<<endl;
164 cin>>v>>a;
165
166 while (1>0){
167 cout<<"Выберите режим работы программы:"<<endl;
168 cout<<"1 - Координаты, рассчитанные по формуле, при движении без сопротивления воздуха"<<endl;
169 cout<<"2 - Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости"<<endl;
170 cout<<"3- Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости"<<endl;
171 cout<<"4 - Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости"<<endl;
172 cout<<"5 - Выйти";
173 cin>>o;
174
175 if (o==1)
176 rez_1(v,a);
177 if (o==2)
178 {
179 cout<<"Введите массу тела и коэф сопротивления воздуха:"<<endl;
180 cin>>m>>k;
181 rez_2(v,a,k,m);
182 }
183
184 if (o==3)
185 {
186 cout<<"Введите массу тела и коэф сопротивления воздуха:"<<endl;
187 cin>>m>>k;
188 rez_3(v,a,k,m);
189 }
190 if (o==4)
191 {
192 cout<<"Введите массу тела и коэф сопротивления воздуха:"<<endl;
193 cin>>m>>k;
194 rez_4(v,a,k,m);
195 }
196 if (o==5)
197 break;
198
199 }
200 }
Описание программы: при запуске пользователь вводит шаг функции, угол, под которым бросают тело, массу тела, сопротивление воздуха и скорость. Программа записывает в четыре файла результаты вычисления:
- Координаты, рассчитанные по формуле для движения без сопротивления воздуха;
- Координаты, рассчитанные по формуле для движения с учетом сопротивления воздуха;
- Координаты, полученные методом Верле при квадратичной зависимости силы сопротивления воздуха от скорости.
- Координаты, полученные методом Верле при линейной зависимости силы сопротивления воздуха от скорости;
Скачать можно тут.
Визуализированный результат работы программы
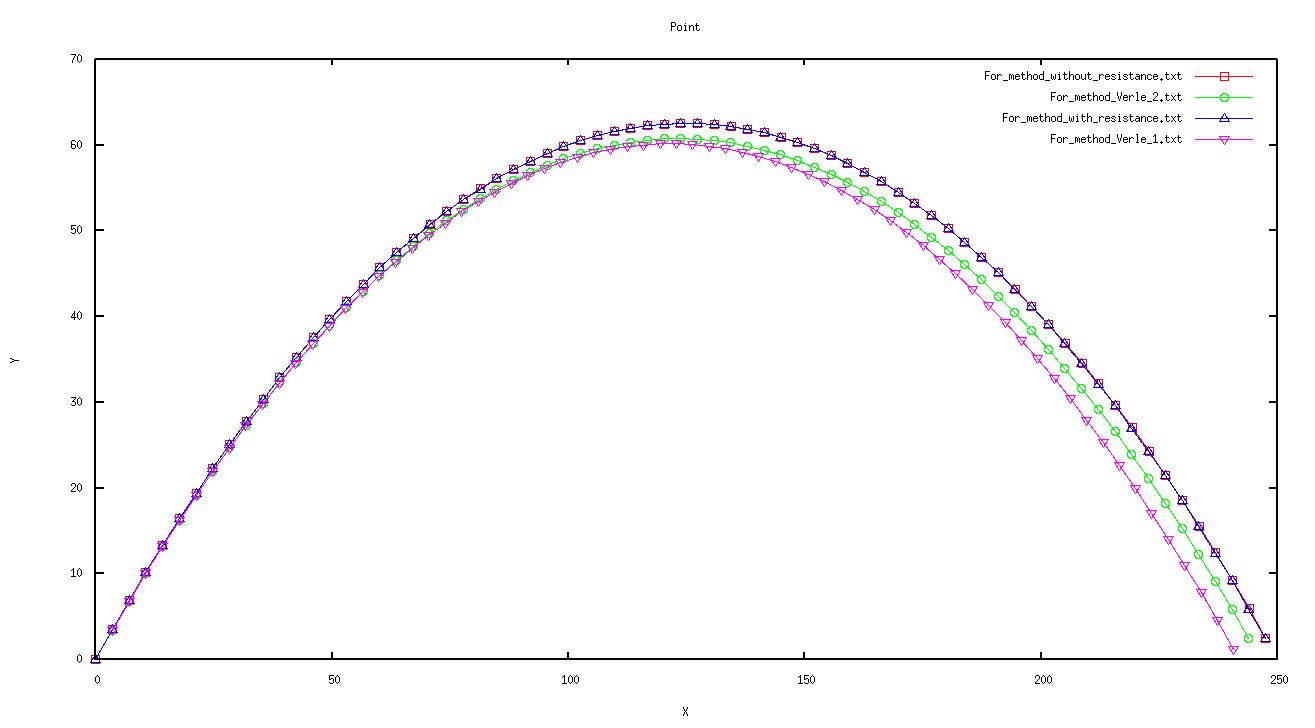
Графики приведены для движения тела массой 1, со скоростью 50, под углом 45 градусов. Сопротивление воздуха принято равным 0.0001, шаг 0,1.
1 #include <iostream> ///программа, подсчитывающая и записывающая в файл координаты движения тела для двух вариантов метода Верле
2 #include <fstream> /// и для движений с учётом сопротивления и без его учёта
3 #include <math.h>
4 #include<stdlib.h>
5 using namespace std;
6
7 int main()
8 {
9 double a, step, Pi, g, Vo, m, r;
10 ///а - угол, под которым движется тело, step - шаг функции, Vo - начальная скорость тела, m - масса тела, r - величина сопротивления
11
12 double x, y, x_0, y_0, x0, y0, Vx, Vy;
13 ///переменные для движения точки без учёта сопротивления и с его учётом
14 ///х - изменяющаяся пошагово координата тела по оси Ох, у - изменяющаяся пошагово координата тела по оси Оу,
15 ///х0 - начальная координата тела по оси Ох, у0 - начальная координата тела по оси Оу
16 ///Vx - скорость тела по оси Ох, Vу - скорость тела по оси Оу
17 ///x_0 - изменяющаяся пошагово координата тела по оси Ох с учётом сопротивления, у_0 - изменяющаяся пошагово координата тела по оси Оу с учётом сопротивления
18
19 double Vy0, Vx0, x1, x2, x3, y1, y2, y3, Vxn, Vyn, Vn;
20 ///переменные для 1го варианта метода Верле
21 ///х1 - координата тела по оси Ох на (n-1) шаге, х2 - координата тела по оси Ох на (n) шаге, х3 - координата тела по оси Ох на (n+1) шаге
22 ///у1 - координата тела по оси Оу на (n-1) шаге, у2 - координата тела по оси Оу на (n) шаге, у3 - координата тела по оси Оу на (n+1) шаге
23 ///Vx0 - начальная скорость тела по оси Ох, Vy0 - начальная скорость тела по оси Оу
24 ///Vxn - скорость тела в данный момент времени по оси Ох, Vyn - скорость тела в данный момент времени по оси Оу
25
26 double Vxn2, Vyn2, x_1, x_2, x_3, y_1, y_2, y_3;
27 ///переменные для 2го варианта метода Верле
28 ///х_1 - координата тела по оси Ох на (n-1) шаге, х_2 - координата тела по оси Ох на (n) шаге, х_3 - координата тела по оси Ох на (n+1) шаге
29 ///у_1 - координата тела по оси Оу на (n-1) шаге, у_2 - координата тела по оси Оу на (n) шаге, у_3 - координата тела по оси Оу на (n+1) шаге
30 ///Vxn2 - скорость тела в данный момент времени по оси Ох, Vyn2 - скорость тела в данный момент времени по оси Оу
31
32 g=10; ///значение ускорения свободного падения
33 Pi=3.14159265; /// значение числа П, используем для перевода радиан в градусы
34
35 do ///цикл, запрашивающий ввод пользователем значения шага функции
36 {
37 cout << "Input the step, it must be less than 1" << endl; ///ввод с клавиатуры шага(то же самое, что дельта t), шаг должен быть маленьким (меньше 1)
38 cin >> step; ///вывод величины шага на экран
39 }
40 while (step>=1); ///выход из цикла не будет обеспечен, пока пользователь не введет число, меньшее 1
41
42 cout << '\n' << "Input the corner in degrees,the corner is in the range from 0 to 90 degrees" << endl; ///ввод с клавиатуры угла в радианах (угол от 0 до 90 градусов)
43 cin >> a; ///вывод значение угла на экран
44 a=(Pi*a)/180.0;
45 cout << '\n' << "Input the weight" << endl; ///ввод с клавиатуры значения массы
46 cin >> m; ///вывод величины массы на экран
47
48 do ///цикл, запрашивающий ввод пользователем значения сопротивления воздуха
49 {
50 cout << '\n' << "Input the value of the resistance, it must be less than 1" << endl; ///ввод с клавиатуры величины сопротивления
51 cin >> r; ///вывод значения сопротивления на экран
52 }
53 while (r>=1); ///выход из цикла не будет обеспечен, пока пользователь не введет число, меньшее 1
54
55 cout << '\n' << "Input the speed" << endl; ///ввод с клавиатуры значения начальной скорости
56 cin >> Vo; ///вывод значения скорости на экран
57
58 ///для движения без учёта сопротивления
59 x0=0; ///обнуление переменных
60 y0=0;
61 x=0;
62 y=0;
63
64 ///для движения с учётом сопротивления
65 x_0=0; ///обнуление переменных
66 y_0=0;
67
68 ///для 1го варианта метода Верле
69
70 Vx0=Vo*cos(a); ///расчет проекции начальной скорости по оси Ох
71 Vy0=Vo*sin(a); ///расчет проекции начальной скорости по оси Оу
72
73 x2=0; ///обнуление переменных
74 y2=0;
75 x3=0;
76 y3=0;
77
78 y1=y2-Vy0*step; ///расчет начального значения координаты по оси Оу
79 x1=x2-Vx0*step; ///расчет начального значения координаты по оси Ох
80
81 ///для 2го варианта метода Верле
82
83 x_2=0; ///обнуление переменных
84 y_2=0;
85 x_3=0;
86 y_3=0;
87
88 Vxn2=Vo*cos(a); ///расчет скорости тела на начальный момент времени по оси Ох
89 Vyn2=Vo*sin(a); ///расчет скорости тела на начальный момент времени по оси Оу
90
91 y_1=y_2-Vo*sin(a)*step; ///расчет начального значения координаты на (п-1) шаге по оси Оу
92 x_1=-Vo*cos(a)*step; ///расчет начального значения координаты на (п-1) шаге по оси Ох
93
94 ofstream out("For method without resistance.txt");
95 ///запись в файл значений координат по осям Ох и Оу для движения без сопротивления
96
97 for (int i=0; y>=0; ++i) ///цикл для подсчета координат при движении тела без учёта сопротивления
98 {
99 x=Vo*step*i*cos(a); ///расчет координаты тела по оси х
100 y=Vo*sin(a)*i*step-(g*i*step*i*step)*0.5; ///расчет координаты тела по оси y
101
102 out << x << " " << y <<'\n'; ///вывод всех значений координат по оси х и по оси у при движении тела без учёта сопротивления
103 }
104 out.close();
105
106 ofstream out1 ("For method with resistance.txt");
107 ///запись в файл значений координат по осям Ох и Оу для движения с учётом сопротивления
108
109 for (int i=0; y_0>=0; ++i) ///цикл для подсчета координат при движении тела с учётом сопротивления
110 {
111 Vx=Vo*cos(a); ///расчет скорости тела по оси Ох
112 Vy=Vo*sin(a); ///расчет скорости тела по оси Оу
113 x_0=x0+(m/r)*Vx*(1.0 - exp((-r*i*step)/m)); ///расчет координаты тела по оси х
114 y_0=y0+(m/r)*(Vy+g*(m/r))*(1.0 - exp((-r*i*step)/m))-g*i*step*(m/r); ///расчет координаты тела по оси y
115
116 out1 << x_0 << " " << y_0 <<'\n'; ///вывод всех значений координат по оси х и по оси у при движении c учётом сопротивления
117 }
118 out1.close();
119
120 ofstream out2 ("For method Verle 1.txt");
121 ///запись в файл значений координат по осям Ох и Оу для 1го варианта метода Верле
122
123 for (int i=0; y3>=0; ++i) ///цикл для подсчета координат и скорости по времени для 1го варианта метода Верле
124 {
125 x3=2*x2-x1-(r/m)*Vn*Vxn*step*step; ///расчет координаты в данный момент времени по оси Ох
126 y3=2*y2-y1-(g+(r/m)*Vn*Vyn)*step*step; ///расчет координаты в данный момент времени по оси Оу
127 Vxn=(x3-x1)/(2.0*step); ///расчет скорости в данный момент времени по оси Оу
128 Vyn=(y3-y1)/(2.0*step); /// расчет скорости в данный момент времени по оси Ох
129 Vn=sqrt(Vxn*Vxn+Vyn*Vyn); ///расчет скорости тела по модулю
130
131 x1=x2; ///присваивание значению координаты х1 на (n-1) шаге значение координаты х2 на n шаге
132 x2=x3; ///присваивание значению координаты х2 на (n) шаге значение координаты х3 на (n+1) шаге
133 y1=y2; ///присваивание значению координаты у1 на (n-1) шаге значение координаты у2 на n шаге
134 y2=y3; ///присваивание значению координаты у2 на (n) шаге значение координаты у3 на (n+1) шаге
135
136 out2 << x3 << " " << y3 <<'\n'; ///вывод всех значений координат по оси Ох и по оси Оу на экран для 1го варианта метода Верле
137 }
138 out2.close();
139
140 ofstream out3 ("For method Verle 2.txt");
141 ///запись в файл значений координат по осям Ох и Оу для 2го варианта метода Верле
142
143 for (int i=0; y_3>=0; ++i) ///цикл для подсчета координат и скорости по времени для 2го варианта метода Верле
144 {
145 x_3=2*x_2-x_1-(r/m)*Vxn2*step*step; ///расчет координаты в данный момент времени по оси Ох
146 y_3=2*y_2-y_1-(g+(r/m)*Vyn2)*step*step; ///расчет координаты в данный момент времени по оси Оу
147 Vxn2=(x_3-x_1)/(2.0*step); ///расчет скорости в данный момент времени по оси Оу
148 Vyn2=(y_3-y_1)/(2.0*step); ///расчет скорости в данный момент времени по оси Ох
149
150 x_1=x_2; ///присваивание значению координаты х_1 на (n-1) шаге значение координаты х_2 на n шаге
151 x_2=x_3; ///присваивание значению координаты х_2 на (n) шаге значение координаты х_3 на (n+1) шаге
152 y_1=y_2; ///присваивание значению координаты у_1 на (n-1) шаге значение координаты у_2 на n шаге
153 y_2=y_3; ///присваивание значению координаты у_2 на (n-1) шаге значение координаты у_3 на (n+1) шаге
154
155 out3 << x_3 << " " << y_3 <<'\n'; ///вывод на экран всех значений координат по оси Ох и по оси Оу для 2го варианта метода Верле
156
157 }
158 out3.close();
159
160 cout << '\n' << "All results are saved in files." << endl; ///вывод на экран сообщения о записи в файл всех результатов
161 cout << '\n' << "The program is finished." << endl; ///вывод на экран сообщения о завершении работы программы
162 return 0;
163 }
Описание программы: программа записывает в четыре файла результаты вычисления:
- Координаты, рассчитанные по формуле, при движении без сопротивления воздуха;
- Координаты, полученные методом Верле при линейной зависимости силы сопротивлении воздуха от скорости;
- Координаты, полученные из точного решения, при линейной зависимости силы сопротивлении воздуха от скорости;
- Координаты, полученные методом Верле при квадратичной зависимости силы сопротивлении воздуха от скорости.