Изгиб балки с V-model взаимодействием — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
Строка 66: Строка 66:
 
</math><br />
 
</math><br />
  
 +
===Алгоритм===
 +
 +
На каждом временном шагу для каждой из частиц суммируются силы и моменты её взаимодействия с соседними частицами. Далее по второму закону Ньютона вычисляются ускорение и угловое ускорение. Координаты частицы и угловая скорость интегрируются методом Leapfrog. Далее по известному значению угловой скорости интегрируется кватернион вращения частицы и осуществляется поворот её базиса(n).
 +
 +
<math> L(t + \Delta t) = L(t) + \frac{1}{2}\omega(t + \Delta t) \circ L(t)
 +
</math><br />
 +
 +
<math> n(t + \Delta t) = L(t + \Delta t) \circ n(0) \circ L'(t + \Delta t)
 +
</math><br />
  
 
== Ссылки ==
 
== Ссылки ==

Версия 10:51, 28 января 2019

Курсовые работы 2018-2019 учебного года > Изгиб балки c V-model взаимодействием

Курсовой проект по Механике дискретных сред

Исполнитель: Абрамов Игорь

Группа: 43604/1

Семестр: осень 2018

Постановка задачи

Создание модели и визуализация изгиба балки с V-model взаимодействием.

Решение

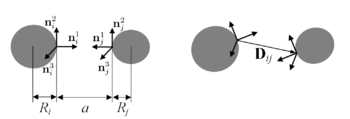
Балка моделируется как система частиц, каждая из которых взаимодействует с двумя ближайшими соседями. Для ориентация каждой [math]i-[/math]ой частицы в пространстве используется жёстко связанный с ней в центре частицы базис [math]\mathbf{n}_{i1}, \mathbf{n}_{i2}, \mathbf{n}_{i3}[/math]. Также введём два вектора

[math] \mathbf{r}_{ij}=\mathbf{r}_i - \mathbf{r}_j [/math]

[math] \mathbf{e}_{ij} = \mathbf{r}_{ij} / r_{ij} [/math]

Вектор [math]\mathbf{D}_{ij}[/math] - соединяет базисы, связанные с соответствующими частицами, поэтому в данной постановке он равен [math]\mathbf{r}_{ij}[/math]. Вектор [math]\mathbf{e}_{ij} = \mathbf{r}_{ij} / r_{ij}[/math] - единичный, сонаправленный [math]\mathbf{r}_{ij}[/math].

Потенциальная энергия связи:

Взаимодействие двух частиц

[math] U = \frac{B_1}{2}(D_{ij}-a)^2 + \frac{B_2}{2}(\mathbf{n}_{j1}-\mathbf{n}_{i1})\cdot\mathbf{d}_{ij} + B_3 \mathbf{n}_{i1}\cdot\mathbf{n}_{j1} - \frac{B_4}{2}(\mathbf{n}_{i2}\cdot\mathbf{n}_{j2} + \mathbf{n}_{i3}\cdot\mathbf{n}_{j3}) [/math]

Таким образом, уравнения для сил и моментов принимают следующий вид:

[math] \mathbf{M}^{TB} = B_3 \mathbf{n}_{j1} \times \mathbf{n}_{i1} - \frac{B_4}{2}(\mathbf{n}_{j2}\times\mathbf{n}_{i2} + \mathbf{n}_{j3}\times\mathbf{n}_{i3}) [/math]
[math] \mathbf{F}_{ij} = B_1(r_{ij}-a)\mathbf{r}_{ij} + \frac{B_2}{2r_{ij}}(\mathbf{n}_{j1} - \mathbf{n}_{i1} -\mathbf{e}_{ij}\cdot(\mathbf{n}_{j1} - \mathbf{n}_{i1})\mathbf{e}_{ij}) [/math]
[math] \mathbf{M}_{ij} = -\frac{B_2}{2}\mathbf{e}_{ij}\times\mathbf{n}_{i1} + \mathbf{M}^{TB} [/math]
[math] \mathbf{M}_{ji} = \frac{B_2}{2}\mathbf{e}_{ij}\times\mathbf{n}_{j1} - \mathbf{M}^{TB} [/math]

Для балки с короткими связями между частицами параметры модели принимают следующие значения:

[math] B_1 = \frac{ES}{a} [/math]
[math] B_2 = -\frac{2EJ[kAa^2-12J(1+\nu)]}{a[kSa^2+24J(1+\nu)]} [/math]
[math] B_3 = \frac{6kSEJa}{kSa^2+24J(1+\nu)} [/math]

[math] B_4 = \frac{GJ_p}{a} [/math]

Алгоритм

На каждом временном шагу для каждой из частиц суммируются силы и моменты её взаимодействия с соседними частицами. Далее по второму закону Ньютона вычисляются ускорение и угловое ускорение. Координаты частицы и угловая скорость интегрируются методом Leapfrog. Далее по известному значению угловой скорости интегрируется кватернион вращения частицы и осуществляется поворот её базиса(n).

[math] L(t + \Delta t) = L(t) + \frac{1}{2}\omega(t + \Delta t) \circ L(t) [/math]

[math] n(t + \Delta t) = L(t + \Delta t) \circ n(0) \circ L'(t + \Delta t) [/math]

Ссылки

Источник — «http://tm.spbstu.ru/?title=Изгиб_балки_с_V-model_взаимодействием&oldid=52614»