Задача 48.44 — различия между версиями
Sankot (обсуждение | вклад) (Новая страница: «== Решение задачи 48.44 из Мещерского == Визуализация 3D-задачи по динамике на JavaScript Исполни…») |
Sankot (обсуждение | вклад) (→Решение) |
||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 10: | Строка 10: | ||
==Условие задачи== | ==Условие задачи== | ||
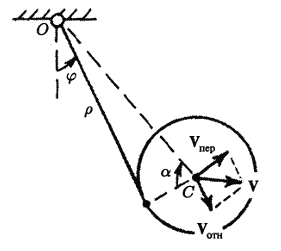
Один конец нерастяжимой тонкой нити обмотан вокруг однородного круглого цилиндра радиуса R, второй конец прикреплен к неподвижной точке O. Цилиндр, разматывая нить, опускается вниз, одновременно раскачиваясь вокруг горизонтальной оси, проходящей через точку подвеса нити. Пренебрегая массой нити, составить дифференциальные уравнения движения цилиндра. | Один конец нерастяжимой тонкой нити обмотан вокруг однородного круглого цилиндра радиуса R, второй конец прикреплен к неподвижной точке O. Цилиндр, разматывая нить, опускается вниз, одновременно раскачиваясь вокруг горизонтальной оси, проходящей через точку подвеса нити. Пренебрегая массой нити, составить дифференциальные уравнения движения цилиндра. | ||
| + | |||
| + | ==Решение== | ||
| + | [[File:48.44.png|thumb|left|Рисунок]] | ||
| + | Уравнение Лагранжа второго рода: | ||
| + | |||
| + | <math>\frac{d}{dt}\left(\frac{\partial L}{\partial\dot q}\right) - \frac{\partial L}{\partial q} = 0 </math> | ||
| + | |||
| + | <math>L = T - Π </math> | ||
| + | |||
| + | Система имеет две степени свободы: длина нити ρ и угол между нитью и вертикальной осью φ. | ||
| + | |||
| + | <math> q1 = ρ, q2 = φ </math> | ||
| + | |||
| + | Движение цилиндра плоское, его кинетическая энергия: | ||
| + | |||
| + | <math> T = \frac{1}{2}mv^{2} + \frac{1}{2}Ϳω^{2} </math> | ||
| + | |||
| + | Где V - скорость центра масс, распишем ее как | ||
| + | |||
| + | <math>V = Vпер - Vотн </math> | ||
| + | |||
| + | <math>Vпер = \dot φOC </math>, <math> OC = \sqrt{R^{2} + ρ^{2}} </math>, <math> Vотн = \dot ρ </math> | ||
| + | |||
| + | <math>V^{2} = \dot φ^{2}(R^{2} + ρ^{2}) + \dot ρ^{2} - 2\dot ρ\dot φ\sqrt{R^{2} + ρ^{2}}cosα</math> | ||
| + | |||
| + | где | ||
| + | |||
| + | <math>cosα = \frac{R}{OC} = \frac{R}{\sqrt{R^{2} + ρ^{2}}}</math> | ||
| + | |||
| + | Учитывая что | ||
| + | |||
| + | <math>Ϳ = \frac{1}{2}mR^{2}, ω = \frac{Vотн}{R} - \dot φ = \frac{\dot ρ}{R} -\dot φ</math> | ||
| + | |||
| + | получаем выражение: | ||
| + | |||
| + | <math>T = \frac{1}{2}m(\dot φ^{2} (R^{2} + ρ^{2}) + \dot ρ^{2} - 2\dot ρ\dot φR) + \frac{1}{4}m(\frac{\dot ρ}{R} - \dot φ)^{2}</math> | ||
| + | |||
| + | Потенциальная энергия: | ||
| + | |||
| + | <math>Π = -mg(ρcosφ - Rsinφ)</math> | ||
| + | |||
| + | Находим | ||
| + | |||
| + | <math>\frac{\partial L}{\partial \dot ρ} = m(\dot ρ - \dot φ R + \frac{1}{2}(\dot ρ - R\dot φ) </math> | ||
| + | |||
| + | <math>\frac{\partial L}{\partial \dot φ} = m(\dot φ^{2} (R^{2} + ρ^{2}) - \dot ρ R - \frac{1}{2}(\dot ρ - R\dot φ) </math> | ||
| + | |||
| + | |||
| + | <math>\frac{\partial L}{\partial ρ} = m(ρ\dot φ^{2} + gcosφ) </math> | ||
| + | |||
| + | <math>\frac{\partial L}{\partial φ} = -mg(ρsinφ - Rcosφ) </math> | ||
| + | |||
| + | |||
| + | Ответ: | ||
| + | |||
| + | <math>\ddot ρ - \ddot φ R - \frac{2}{3}ρ\dot φ - \frac{2}{3}gcosφ = 0</math> | ||
| + | |||
| + | <math>ρ^{2}\ddot φ + 2\dot φ\dot ρ ρ - Rρ\dot φ^{2} + gρsinφ = 0</math> | ||
==Визуализация== | ==Визуализация== | ||
{{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Sankova_TN/48.44/111.html }} | {{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Sankova_TN/48.44/111.html }} | ||
Текущая версия на 21:23, 25 января 2018
Решение задачи 48.44 из Мещерского[править]
Визуализация 3D-задачи по динамике на JavaScript
Исполнитель: Санькова Татьяна
Группа 23632/2 Кафедра Теоретической механики
Условие задачи[править]
Один конец нерастяжимой тонкой нити обмотан вокруг однородного круглого цилиндра радиуса R, второй конец прикреплен к неподвижной точке O. Цилиндр, разматывая нить, опускается вниз, одновременно раскачиваясь вокруг горизонтальной оси, проходящей через точку подвеса нити. Пренебрегая массой нити, составить дифференциальные уравнения движения цилиндра.
Решение[править]
Уравнение Лагранжа второго рода:
Система имеет две степени свободы: длина нити ρ и угол между нитью и вертикальной осью φ.
Движение цилиндра плоское, его кинетическая энергия:
Где V - скорость центра масс, распишем ее как
, ,
где
Учитывая что
получаем выражение:
Потенциальная энергия:
Находим
Ответ:
Визуализация[править]