Задача многих тел в небесной механике

«Я есмь Альфа и Омега, начало и конец...» (Откр 1:8)

Небесная механика — раздел астрономии, применяющий законы механики для изучения движения небесных тел. Естественно, что небесная механика в первую очередь изучает поведение тел Солнечной системы — обращение планет вокруг Солнца, спутников вокруг планет, движение комет и других малых небесных тел. Теоретический фундамент, на котором построена небесная механика и механика космического полета − это закон всемирного тяготения Ньютона: две материальные точки, обладающие массами [math]m[/math] и [math]M[/math], тяготеют друг к другу с силой

[math] {\bf F}_{12}=\frac{Gm M}{r^3} {\bf r}_{12} [/math]

[math]{\bf r}_{12}={\bf r}_{1}-{\bf r}_{2}[/math]

[math]G=6.67 \cdot \frac{10^{-8}{см^3}}{г \cdot сек^3} [/math]

Если рассматривать движение одной из этих точек [math]m[/math] относительно другой [math]M[/math], считая, что можно пренебречь всеми силами, кроме гравитационной, то дифференциальные уравнения движения получат вид:

[math]{\ddot x}_i +\frac{G(m+M)x_i}{r^3}=0; i=1,2,3[/math]

Это уравнение легко интегрируется в элементарных функциях.

«И ты будешь вечно идти, и не будет тебе ни покоя, ни смерти». (Легенда об Агасфере.)

Результаты интегрирования:

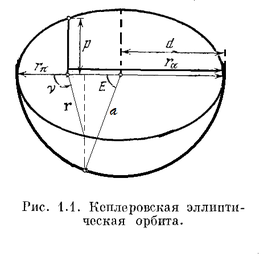
Спутник может двигаться по эллиптической или параболической или гиперболической орбите в зависимости от величины эксцентриситета. Нас интересует,конечно, случай эллиптической орбиты.

[math]r=\frac{p}{1+\varepsilon cos\nu}[/math]

рис. 1

[math]p=\frac{2r_a r_ \pi }{r_a+r_\pi}[/math]

[math]\varepsilon=\frac{r_a-r_\pi}{r_a+r_\pi}[/math]

Экцентрическая аномалия [math]Е[/math] связана со временем [math]t[/math] уравнением Кплера

[math]E-\varepsilon sin E =n(t-\tau_\pi^{"*"})[/math] ,где

[math]n=\sqrt{G M/a^3}[/math] так называемое среднее движение;

[math]a=\frac{r_a+r_\pi}2[/math]

Постоянная [math]\tau_\pi^{"*"}[/math] обозначает момент прохождения через перигей орбиты

Из этого соотношения выводится все параметры классической орбиты: Период обращения спутника, модуль скорости на данном участке орбиты,и два интеграла движения (интеграл энергии и вектор Лапласса).

«И познаете истину, и истина сделает вас свободными» (Ин. 8:32)

[math]\ddot x_i+\frac{G(m+M) x_i}{r^3}=f_i[/math] -учтём действие сторонних сил.

[math]i=1,2,3[/math]

[math]\sqrt{\sum f^2_i}\lt \lt \frac{G\mu}{r^2}[/math]- условие малости их величины.

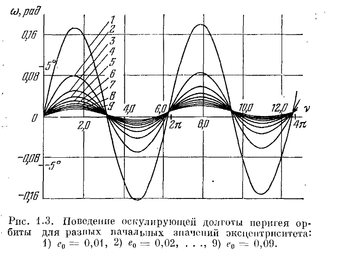
Тогда некоторые пораметры орбиты спутника будут оскулировать. (Например, долгота перигелия орбиты, как на рисунке 2.(Также будет иметь место его систематический вековой уход, накапливающийся от поворота к повороту спутника))

left/рис 2

«Во многой мудрости много печали, и кто умножает познания, умножает скорбь.» (Еккл 1:18)

Рассмотрим один интересный пример:

рис. 3

Формулировка задачи: В пустоте находятся n материальных точек, взаимодействующих по закону всемирного тяготения Ньютона. Заданы начальные положения и скорости точек. Требуется найти положения точек для всех последующих моментов времени.

Математические трудности исследования этой задачи быстро возрастают с ростом числа тел. Для произвольного n задача не решена до сих пор, хотя существует много аналитических и численных методов, ориентированных на использование компьютеров, которые могут дать приближенное решение задачи. Это решение позволяет для заданных конкретных начальных условий определить положение каждой из n точек с любой необходимой для практики точностью для любого конечного отрезка времени. Но эти методы неспособны дать ответ на вопрос о поведении точек на сколь угодно большом неограниченном промежутке времени, хотя этот вопрос крайне важен в задаче о будущей судьбе Солнечной системы, да и всего мироздания тоже.

Но есть решения для частных случаев.

Случай [math]n = 1[/math]. Решение задачи о движении одного тела содержится уже в первом законе Ньютона - законе инерции: всякое тело удерживается в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не побуждается приложенными силами изменить это свое состояние.

Случай [math]n = 2[/math]. Решение задачи двух тел также было получено Ньютоном.Он открыл закон всемирного тяготения, то есть по заданному движению планеты была найдена сила ее взаимодействия с Солнцем. Ньютон рассмотрел и обратную задачу (в данном случае задачу двух тел). Оказалось, что тела движутся в фиксированной плоскости, определяемой начальными условиями, а их орбиты друг относительно друга и относительно общего центра масс представляют собой кривые, называемые коническими сечениями.

В 1772 году Лагранж опубликовал свой знаменитый мемуар "О задаче трех тел", удостоенный впоследствии премии Парижской академии наук. В нем, занимаясь уравнениями задачи трех тел, Лагранж, между прочим, указывает на существование двух классов движений в задаче трех тел, которые описываются несложными математическими формулами.

Для движений одного класса три взаимно притягивающиеся по закону Ньютона точки P1 , P2 и P3 , расположенные в вершинах равностороннего треугольника произвольных размеров, при определенных по величине и направлению скоростях будут и в последующем двигаться, постоянно образуя равносторонний треугольник. Величина стороны треугольника изменяется со временем согласно законам Кеплера, а сам треугольник вращается в фиксированной плоскости вокруг общего центра масс тел, также подчиняясь законам Кеплера. Частные решения этого класса называют треугольными, или лагранжевыми, решениями.

В движениях второго класса все три тела постоянно находятся на одной прямой, вращающейся вокруг общего центра масс тел в соответствии со вторым законом Кеплера, а расстояния между телами изменяются опять же по законам кеплеровских движений. Существование таких частных решений было отмечено Леонардом Эйлером в 1767 году, за пять лет до мемуара Лагранжа. Решения второго класса получили название прямолинейных (коллинеарных), или эйлеровых.

Траектории тел P1 , P2 и P3 , соответствующие точным решениям задачи трех тел, показаны на рис. 3. Представлен случай эллиптического движения. Точками на рисунке отмечены положения тел для трех (двух) моментов времени.

Существование упомянутых точных решений задачи трех тел можно доказать элементарными средствами. Особенно просто это можно сделать, когда тела движутся относительно их общего центра масс по круговым орбитам. Не останавливаясь на подробностях, отметим только, что в этом случае доказательство может быть основано на том, что центробежная сила для каждого из тел, вращающихся вокруг общего центра масс, должна уравновешиваться силами притяжения двух других тел.

«Много замыслов в сердце человека, но состоится только определенное Господом.» (Притчи 19:21)

Для небесной механики и динамики космических полетов наиболее важна так называемая ограниченная задача трех тел. Она состоит в изучении движения тела P малой массы m3 под действием ньютоновского притяжения тел [math]S[/math] и [math]J[/math], обладающих конечными массами [math]m1[/math] и [math]m2[/math] ([math]m1 \gt = m2 \gt \gt m3[/math]) в предположении, что тело малой массы не влияет на движение тел конечных масс.

Тем самым в ограниченной задаче тела [math]S[/math] и [math]J[/math] движутся по орбитам, определяемым задачей двух тел, так что их движение известно. Таким образом, анализ ограниченной задачи трех тел сводится к исследованию движения только одного тела [math]P[/math] малой массы. Например, если пренебречь притяжением Солнца, то движение космического аппарата на трассе Земля-Луна с приемлемой точностью описывается в рамках ограниченной задачи трех тел.

Конечно, ограниченная задача значительно проще общей (неограниченной) задачи трех тел, но и ее общее решение не найдено.

В зависимости от формы орбит тел [math]S[/math] и [math]J[/math] конечных масс можно различать гиперболическую, параболическую и эллиптическую ограниченные задачи трех тел. Когда тела [math] S[/math] и [math]J[/math] движутся по окружностям, то говорят о круговой ограниченной задаче. Если тело [math]P[/math] малой массы во все время движения находится в плоскости движения тел [math]S[/math] и [math] J[/math], то говорят, что соответствующая ограниченная задача плоская. Если же тело [math]P[/math] в своем движении выходит из плоскости орбит тел [math]S[/math] и [math]J[/math], то говорят о пространственной ограниченной задаче.

Со многих точек зрения удобно изучать движение тела [math]P[/math] в системе координат, вращающейся вместе с телами [math]S[/math] и [math]J[/math], выбрав единицу длины такой, чтобы и для некруговой задачи расстояние между телами [math]S[/math] и [math]J[/math] было постоянным. В этой системе координат упомянутым выше точным решениям задачи трех тел соответствуют фиксированные точки - положения равновесия тела [math]P[/math]. Точки, лежащие на прямой, проходящей через [math]S[/math] и [math]J[/math], обозначают через [math]L_1[/math] , [math]L_2[/math] и [math]L_3[/math] , а точки, образующие равносторонние треугольники с телами [math]S[/math] и [math]J[/math], обозначают через [math]L_4[/math] и [math]L_5[/math] . Если тело [math]P[/math] поместить в[math] L_i[/math] с нулевой (во вращающейся системе координат) скоростью, то оно останется неподвижным. Точки [math]L_i[/math] часто называют точками либрации или либрационными центрами; [math]L_4[/math] и [math]L_5[/math] - треугольные, а [math]L_1 , L_2 , L_3[/math] - прямолинейные (коллинеарные) точки либрации.

Задача об устойчивости прямолинейных точек либрации оказалась сравнительно несложной. Она решена давно, причем с отрицательным выводом - все три точки [math]L_1 , L_2[/math] и [math]L_3[/math] неустойчивы. Это значит, что частицы космической материи, попадающие в окрестность прямолинейной точки либрации, с течением времени выбрасываются из этой окрестности.

Вопрос об устойчивости треугольных точек либрации оказался более трудным. В большинстве случаев они будут утойчивы.

«Что было, то и будет; и что делалось, то и будет делаться, и нет ничего нового под Солнцем.» (Еккл 1:8)

Проблема устойчивости Солнечной системы начала интересовать учёных сразу после открытия закона всемирного тяготения. Первое исследование в этой области принадлежит автору термина «небесная механика» Пьеру Лапласу. В 1773 году он доказал теорему примерно следующего содержания: «если движение планет происходит в одном направлении, их массы одного порядка, эксцентриситеты и наклоны малы, а большие полуоси испытывают лишь небольшие колебания относительно среднего положения, то эксцентриситеты и наклоны орбит будут оставаться малыми на рассматриваемом интервале»[1]. То есть при указанных, крайне ограниченных условиях, Солнечная система была бы стабильной.

Другая значительная попытка доказать устойчивость или неустойчивость Солнечной системы была предпринята А. Н. Колмогоровым, В. И. Арнольдом и Ю. Мозером в 60-х годах XX века (так называемая КАМ-теория). Ими была доказана теорема примерно следующего содержания: «если массы планет достаточно малы, эксцентриситеты и наклоны орбит малы, то для большинства начальных условий (исключая резонансные и близкие к ним) движение будет условно-периодическим, эксцентриситеты и наклоны будут оставаться малыми, а большие полуоси будут вечно колебаться вблизи своих первоначальных значений». В солнечной системе есть резонансы, и теорема относится только к системе трёх тел.

Резонансы в солнечной системе.

Самый простой резонанс возникает, если отношение периодов обращения двух планет в Солнечной системе равно отношению двух небольших чисел. В результате резонанса планеты могут передавать друг другу заметные количества момента вращения. Некоторые из известных приближений к резонансам: Нептун и Плутон, периоды обращения которых относятся почти как 3:2, система Юпитер-Сатурн (приближение к 2:5) и резонанс между Меркурием и Юпитером, у которых близки друг к другу периоды прецессии перигелия.

«...сам сатана принимает вид ангелов света...» (2-е послание к Коринфянам 11:14)

В 90-х годах проводились численные расчёты поведения внешних планет Солнечной системы на интервале времени порядка миллиардов лет. Результаты разных исследователей были противоречивы и показывали как хаотическое, так и регулярное движение планет. Хаотическое движение здесь не означает заметное изменение орбит. Она означает лишь, что нельзя предсказать положение планеты на орбите через интервал времени, больший некоторого предела. Более поздний анализ этих данных показал, что варьированием начальных условий в пределах погрешностей наблюдения можно получать как хаотическое, так и регулярное движение с использованием одного и того же метода. Так что нельзя сказать, какой характер имеет движение внешних планет Солнечной системы.

Для внутренних планет численные расчеты дают хаотичность их положения на орбите. Кроме того, особой проблемой является Меркурий, который, резонансно взаимодействуя с Юпитером, может существенно изменять свою орбиту. В одном из последних исследований моделирование проводилось на интервале времени порядка миллиардов лет и рассчитывалось 2500 вариантов с орбитой Меркурия, изменяющейся с шагом 0,38 мм (в настоящий момент погрешность её измерений порядка метров). Среди этих вариантов обнаружено 20 решений, где орбита Меркурия приобретает достаточный эксцентриситет для пересечения орбит Венеры, Земли и Марса. Среди этих орбит есть такие, что Меркурий падает на Солнце, сталкивается с другими внутренними планетами, либо дестабилизирует их орбиты так, что они сами сталкиваются друг с другом.