Диффузия под напряжением в задачах механохимии — различия между версиями
Polina (обсуждение | вклад) |
Polina (обсуждение | вклад) (→Список литературы) |
||
| (не показано 19 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | '''БАКАЛАВРСКАЯ РАБОТА'''<br> | |
| − | + | ''Автор работы'': [[Григорьева Полина]]<br> | |
| + | ''Научный руководитель'': [[Елена Вильчевская]]<br> | ||
| + | |||
== Введение == | == Введение == | ||
Проблема термического окисления кремния сегодня является одной из важнейших проблем в химии в связи с широким использованием и значимостью технологии кремниевых интегральных схем. Так как объем молекулы диоксида кремния примерно в 2.3 раза больше атома кремния, окисление кремния сопровождается большим увеличением объема. Это значит, что эта проблема принадлежит области механохимии, которая рассматривает химические реакции под действием механических нагрузок. | Проблема термического окисления кремния сегодня является одной из важнейших проблем в химии в связи с широким использованием и значимостью технологии кремниевых интегральных схем. Так как объем молекулы диоксида кремния примерно в 2.3 раза больше атома кремния, окисление кремния сопровождается большим увеличением объема. Это значит, что эта проблема принадлежит области механохимии, которая рассматривает химические реакции под действием механических нагрузок. | ||
| Строка 10: | Строка 12: | ||
*Исследовать влияние зависимости коэффициента диффузии от напряжений. | *Исследовать влияние зависимости коэффициента диффузии от напряжений. | ||
| − | == Постановка задачи: Модель == | + | == Постановка задачи: Модель и уравнения == |
| + | Теория кинетики химических реакций основана на концепции химических потенциалов и химического сродства, которые являются линейной комбинацией химических потенциалов веществ, принимающих участие в реакции. В классической теории химический потенциал является скаляром. Однако этот подход действителен только для газов и жидкостей, но редко для твердых тел. Если мы хотим исследовать фазовый переход в деформируемых твердых материалах, нам нужно тензорное выражение для химического потенциала. Это также значит, что химическое сродство тоже станет тензором. | ||
| + | В связи с проблемой, описанной в предыдущем разделе, мы рассмотрим химическую реакцию между твердой и газовой компонентами: | ||
| + | |||
| + | <math> | ||
| + | {n_ - }{B_ - } + {n_*}{B_*} \to {n_ + }{B_ + }, | ||
| + | </math> | ||
| + | |||
| + | где <math>B_ -</math> и <math>B_ +</math> относятся к деформируемым твердым компонентам, а <math>B_*</math> - к газовой компоненте. Мы считаем, что реакция сконцентрирована около фронта реакции, <math>\Gamma </math>, который разделяет области, занятые <math>B_ -</math> и <math>B_ +</math>. Реакция проистекает и продолжается вследствие диффузии газовой компоненты <math>B_*</math> сквозь образующуюся <math>B_ +</math>. Мы считаем, что весь газ, подходящий к фронту, будет израсходован в химической реакции. Как пример такой реакции, мы можем рассмотреть уравнение, описывающее образование диоксида кремния <math>{Si + O_2} \to {SiO_2}</math>. | ||
| + | |||
| + | Мы считаем, что область, занятая <math>B_ +</math>, является проницаемой для газовой компоненты, которая может свободно диффузировать через твердую компоненту и не вызывать в ней никаких деформаций. Для простоты мы не учитываем эффекты внутреннего трения, влияние реакции на температуру, т.е. мы не реашем задачу теплопроводности, и считаем температуру <math>T</math> параметром модели. | ||
| + | |||
| + | Было показано, что нормальная компонента тензора химического сродства может быть вычислена согласно следующей формуле (см.(1)): | ||
| + | |||
| + | <math> | ||
| + | {A_{nn}} = \frac{{{n_ - }{M_ - }}}{{{\rho _ - }}}\left( {\gamma (T) + {\textstyle{1 \over 2}}{{ \boldsymbol{\sigma }}_{^ - }}:{{ \boldsymbol{\varepsilon }}_{^ - }} - {\textstyle{1 \over 2}}{{ \boldsymbol{\sigma }}_{^ + }}:({{ \boldsymbol{\varepsilon }}_{^ + }} - {{ \boldsymbol{\varepsilon }}_{^{{\rm{ch}}}}}) + {{ \boldsymbol{\sigma }}_{^ + }}:({{ \boldsymbol{\varepsilon }}_{^ + }} - {{ \boldsymbol{\varepsilon }}_{^ - }})} \right) + n_*RT\ln \frac{{c(\Gamma )}}{{{c_*}}}\ | ||
| + | </math> | ||
| + | |||
| + | где <math>{\boldsymbol{\sigma }}_{^ - }^{} = {{\bf{C}}_{^ - }}:{{\boldsymbol{\varepsilon }}_{^ - }}</math> и <math>{{\boldsymbol{\sigma }}_{^ + }} = {{\boldsymbol{C}}_{^ + }}:({{\boldsymbol{\varepsilon }}_{^ + }} - {{\boldsymbol{\varepsilon }}_{^{{\rm{ch}}}}})</math> - тензора напряжений Коши, <math>{{\boldsymbol{C}}_{^ \pm }}</math> являются тензорами жесткости упругих компонент, <math>{{\boldsymbol{\varepsilon }}_{^ \pm }}</math> - тензора деформации, <math>c(\Gamma )</math> - концентрация газа на фронте реакции, <math>c_*</math> - растворимость газовой компоненты в сформированном материале <math>B_ +</math>. Также мы относим деформации химических превращений к <math>{{\bf{\varepsilon }}_{^{{\rm{ch}}}}}</math> и считаем, что эти деформации изотропны в объеме, т.е. <math>{{ \boldsymbol{\varepsilon }}_{^{{\rm{ch}}}}} = {\varepsilon _{^{{\rm{ch}}}}}\boldsymbol{I}</math> , где <math>\boldsymbol{I}</math> - единичный тензор. Параметр <math>\gamma (T)</math> отвечает за отсчетные уровни химических энергий. Если температура <math>Т</math> дана, <math>\gamma (T)</math> является параметром модели (более подробно см. (2), (3)). | ||
| + | |||
| + | Если мы заменим скалярную величину химического сродства нормальной компонентой тензора химического сродства, скорость на элементе поверхности с нормалью <math>\boldsymbol{n}</math> будет определяться выражением: | ||
| + | |||
| + | <math> | ||
| + | {\omega _n} = \omega \left\{ {1 - \exp \left( { - \frac{{{A_{nn}}}}{{RT}}} \right)} \right\}, | ||
| + | </math> | ||
| + | |||
| + | где <math>\omega = {k_*}c</math> - скорость прямой химической реакции, <math>{k_*}</math> является кинетической константой скорости химической реакции. Тогда из баланса массы на фронте реакции, <math>n_-M_-\omega=\rho_-V</math>, <math>V</math> - нормальная компонента скорости распространения химического фронта, следует, что : | ||
| + | <math> | ||
| + | V = \frac{{{n_ - }{M_ - }}}{{{\rho _ - }}}\omega \left\{ {1 - \exp \left( { - \frac{{{A_{nn}}}}{{RT}}} \right)} \right\}. | ||
| + | </math> | ||
| − | = | + | Фронт реакции продвигается, только если <math>A_{nn}>0</math>. Тогда из уравнения <math>A_{nn}=0</math> мы можем найти равновесную концентрацию <math>c_{eq}</math> на фронте реакции: |
| + | <math> | ||
| + | \frac{{{n_ - }{M_ - }}}{{{\rho _ - }}}\left( {\gamma (T) + {\textstyle{1 \over 2}}{{\boldsymbol{\sigma }}_{^ - }}:{{\boldsymbol{\varepsilon }}_{^ - }} - {\textstyle{1 \over 2}}{{\boldsymbol{\sigma }}_{^ + }}:({{\boldsymbol{\varepsilon }}_{^ + }} - {{\boldsymbol{\varepsilon }}_{^{ch}}}) + {{\boldsymbol{\sigma }}_{^ + }}:({{\boldsymbol{\varepsilon }}_{^ + }} - {{\boldsymbol{\varepsilon }}_{^ - }})} \right) + {n_*}RT\ln \frac{{{c_{{\rm{eq}}}}}}{{{c_*}}} = 0. | ||
| + | </math> | ||
| + | |||
| + | Вводя эту равновесную концентрацию, мы можем переписать <math>A_{nn}</math> вблизи химического равновесия как <math>{A_{nn}} = {n_*}RT\left( {\frac{{c(\Gamma )}}{{{c_{{\rm{eq}}}}}} - 1} \right)</math>. Следовательно, мы можем переписать и формулу для скорости распространения реакции: | ||
| + | |||
| + | <math> | ||
| + | V = \frac{{{n_ - }{M_ - }}}{{{\rho _ - }}}{k_*}{n_*}(c(\Gamma ) - {c_{{\rm{eq}}}}). | ||
| + | </math> | ||
| + | |||
| + | Концентрация газовой компоненты на фронте химической реакции <math>c(\Gamma )</math> может быть найденa из второго закона Фика для диффузии: | ||
| + | |||
| + | <math> | ||
| + | \frac{{\partial c}}{{\partial t}} = \nabla \cdot (D\nabla c) | ||
| + | </math> | ||
| + | |||
| + | Мы считаем, что процесс диффузии не зависит от времени. Тогда уравнение принимает вид: | ||
| + | <math> | ||
| + | \nabla \cdot (D\nabla c)=0. | ||
| + | </math> | ||
| + | |||
| + | Граничными условиями являются: | ||
| + | <math> | ||
| + | D{\left. {\nabla \cdot c} \right|_\Omega } + \alpha ({c_*} - {\left. c \right|_\Omega }) = 0,\quad D{\left. {\nabla \cdot c} \right|_\Gamma } + {n_*}^2{k_*}(c(\Gamma ) - {c_{{\rm{eq}}}}) = 0. | ||
| + | </math> | ||
| + | |||
| + | Первое условие следует из условия баланса массы на внешней границе тела <math>\Omega</math>, <math>\alpha</math> - константа скорости растворения молекул газа в новом материале. Второе условие следует из условия баланса массы на фронте реакции <math>\Gamma</math>. | ||
| + | Определение коэффициента диффузии используется согласно (4). Коэффициент диффузии может быть подсчитан по следующей формуле: | ||
| + | <math> | ||
| + | D = {D_0}{e^{ - p{V_d}/kT}}, D < {D_{{\rm{max}}}} | ||
| + | </math> | ||
| + | где за <math>p = - {\textstyle{1 \over 3}}\left( {\sigma _{11}^ + + \sigma _{22}^ + + \sigma _{33}^ + } \right)</math> обозначено давление на фронте реакции, <math>T</math> - температура системы, <math>V_d</math> - объем, занимаемый молекулой, и <math>k</math> - температурная постоянная Больцмана. Кроме того, величина <math>D_{{\rm{max}}}/D</math>, варьируется от 1.1 до 2 в зависимости от температуры. | ||
| + | Итак, задача сводится к следующим пунктам: сначала мы находим <math>c_{{\rm{eq}}}</math>. Далее, мы находим <math>c(\Gamma )</math> из задачи диффузии и затем, окончательно, подставляем полученные значения в формулу для нормальной компоненты скорости. | ||
== Решение для различных видов механических нагрузок == | == Решение для различных видов механических нагрузок == | ||
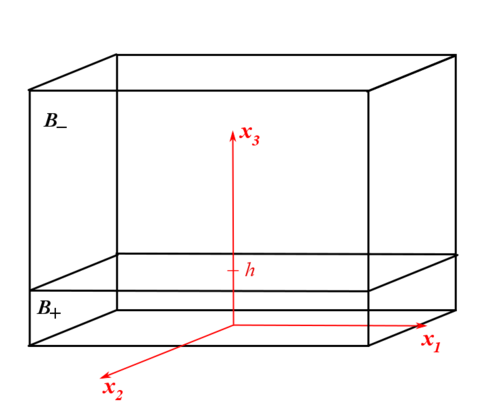
| + | В этом разделе мы представим аналитическое решение задачи для простейшей геометрии. Станем рассматривать трехмерный прямоугольный параллелепипед: <math>{x_1} \in \left[ { - {l_1},{l_1}} \right], \qquad {x_2} \in \left[ { - {l_2},{l_2}} \right], \qquad {x_3} \in \left[ { - {0},{H}} \right]</math> с реакцией, распространяющейся в направлении оси <math>x_3</math> и фронтом реакции, представленным плоскостью <math>x_3 = h</math>. Считаем, что концентрация не зависит от координат <math>x_1</math> и <math>x_2</math>, поэтому <math>c=c(x_3)</math>, <math>c(\Gamma)=c(h)</math>. | ||
| + | [[File:drawing.png|500px]] | ||
| + | |||
| + | |||
| + | Будет изучено два случая механической нагрузки: | ||
| + | первый, перемещения на поверхности тела заданы, и второй, напряжения на поверхности заданы. | ||
| + | |||
| + | Считаем, что нам даны перемещения, которые приложены к телу следующим образом: | ||
| + | |||
| + | |||
| + | <math>u_1^{{ + \mathord{\left/ | ||
| + | {\vphantom { + - }} \right. | ||
| + | } - }}\left( {{x_1} = \pm {l_1},\;\;{x_2} \in \left[ { - {l_2},{l_2}} \right],\;\;{x_3} \in \left\{ \begin{array}{l} | ||
| + | \left( {0,h} \right){\rm{if }} + \\ | ||
| + | \left( {h,H} \right){\rm{if }} - | ||
| + | \end{array} \right.} \right) = u_1^0\nonumber\\ | ||
| + | u_2^{{ + \mathord{\left/ | ||
| + | {\vphantom { + - }} \right. | ||
| + | } - }}\left( {{x_1} \in \left[ { - {l_1},{l_1}} \right],\;\;{x_2} = \pm {l_2},\;\;{x_3} \in \left\{ \begin{array}{l} | ||
| + | \left( {0,h} \right){\rm{if }} + \\ | ||
| + | \left( {h,H} \right){\rm{if }} - | ||
| + | \end{array} \right.} \right) = u_2^0 | ||
| + | </math> | ||
| + | Тогда деформации равномерно распределены по всему телу: | ||
| + | |||
| + | <math> | ||
| + | \varepsilon _{11}^ - = \;\varepsilon _{11}^ + = \varepsilon _{11}^0 = \frac{{u_1^0}}{{{l_1}}}, \qquad \varepsilon _{22}^ - = \;\varepsilon _{22}^ + = \varepsilon _{22}^0 = \frac{{u_2^0}}{{{l_2}}} | ||
| + | </math> | ||
| + | |||
| + | Сдвиговые деформации отсутствуют, т.е. <math>\varepsilon _{ij}^ \pm = 0,i \ne j</math>. | ||
| + | |||
| + | Считаем, что напряжения по оси <math>x_3</math> отсутствуют, т.е. имеем дело с плосконапряженной задачей. | ||
| + | Тогда из закона Гука можем вычислить оставшиеся напряжения и деформации: | ||
| + | |||
| + | <math> | ||
| + | \varepsilon _{33}^ - = - \frac{{{\lambda ^ - }}}{{{\lambda ^ - } + 2{\mu ^ - }}}(\varepsilon _{11}^0 + \varepsilon _{22}^0) | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | \sigma _{11}^ - = {\lambda ^ - }\left( {\varepsilon _{11}^0 + \varepsilon _{22}^0 - \frac{{{\lambda ^ - }}}{{{\lambda ^ - } + 2{\mu ^ - }}}(\varepsilon _{11}^0 + \varepsilon _{22}^0)} \right) + 2{\mu ^ - }\varepsilon _{11}^0\nonumber\\ | ||
| + | |||
| + | \sigma _{22}^ - = {\lambda ^ - }\left( {\varepsilon _{11}^0 + \varepsilon _{22}^0 - \frac{{{\lambda ^ - }}}{{{\lambda ^ - } + 2{\mu ^ - }}}(\varepsilon _{11}^0 + \varepsilon _{22}^0)} \right) + 2{\mu ^ - }\varepsilon _{22}^0 | ||
| + | </math> | ||
| + | |||
| + | Для региона "+": | ||
| + | |||
| + | <math> | ||
| + | {\varepsilon _{33}}^ + = \frac{{{\textstyle{2 \over 3}}{\mu ^ + } - {k^ + }}}{{{k^ + } + {\textstyle{4 \over 3}}{\mu ^ + }}}\left( {\varepsilon _{11}^0 + \varepsilon _{22}^0} \right) + \frac{{3{k^ + }}}{{{k^ + } + {\textstyle{4 \over 3}}{\mu ^ + }}}{\varepsilon _{{\rm{ch}}}} | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | \sigma _{11}^ + = {\lambda ^ + }\left( {\varepsilon _{11}^0 + \varepsilon _{22}^0 - \frac{{{\lambda ^ + }}}{{{\lambda ^ + } + 2{\mu ^ + }}}\left( {\varepsilon _{11}^0 + \varepsilon _{22}^0} \right) + \frac{{3{k^ + }}}{{{\lambda ^ + } + 2{\mu ^ + }}}{\varepsilon _{{\rm{ch}}}}} \right) + 2{\mu ^ + }\varepsilon _{11}^0 - 3{k^ + }{\varepsilon _{{\rm{ch}}}}\nonumber\\ | ||
| + | |||
| + | \sigma _{22}^ + = {\lambda ^ + }\left( {\varepsilon _{11}^0 + \varepsilon _{22}^0 - \frac{{{\lambda ^ + }}}{{{\lambda ^ + } + 2{\mu ^ + }}}\left( {\varepsilon _{11}^0 + \varepsilon _{22}^0} \right) + \frac{{3{k^ + }}}{{{\lambda ^ + } + 2{\mu ^ + }}}{\varepsilon _{{\rm{ch}}}}} \right) + 2{\mu ^ + }\varepsilon _{22}^0 - 3{k^ + }{\varepsilon _{{\rm{ch}}}} | ||
| + | </math> | ||
| + | |||
| + | Для удобства расчетов с значениями параметров конкретного материала перейдем к модулю Юнга, <math>E</math>, и коэффициенту Пуассона, <math>\nu</math>, и запишем выражение для функции напряжений, входящей в состав выражения для вычисления <math>c_{eq}</math>: | ||
| + | |||
| + | <math> | ||
| + | \left( {{\boldsymbol\sigma _ - }:{\boldsymbol\varepsilon _ - } - {\boldsymbol\sigma _ + }:{\boldsymbol\varepsilon _ + } + {\boldsymbol\sigma _ + }:{\boldsymbol\varepsilon _{{\rm{ch}}}}} \right) =\nonumber\\ | ||
| + | \left( {\frac{{{E_ - }}}{{1 - \nu _ - ^2}} - \frac{{{E_ + }}}{{1 - \nu _ + ^2}}} \right)\mathop {\varepsilon _{11}^0}\nolimits^2 + \left( {\frac{{{E_ - }}}{{1 - \nu _ - ^2}} - \frac{{{E_ + }}}{{1 - \nu _ + ^2}}} \right)\mathop {\varepsilon _{22}^0}\nolimits^2 + | ||
| + | {2\left( {\frac{{{\nu _ - }{E_ - }}}{{1 - \nu _ - ^2}} - \frac{{{\nu _ + }{E_ + }}}{{1 - \nu _ + ^2}}} \right)\varepsilon _{11}^0\varepsilon _{22}^0 + \frac{{2{E_ + }}}{{\left( {1 - \nu _ + ^{}} \right)}}\varepsilon _{{\rm{ch}}}^{}(\varepsilon _{11}^0 + \varepsilon _{22}^0) - \frac{{2{E_ + }}}{{\left( {1 - \nu _ + ^{}} \right)}}\varepsilon _{{\rm{ch}}}^2} | ||
| + | </math> | ||
| + | |||
| + | Реакция идет только при <math>{A_{nn}} > 0</math>. Следовательно, при отсутствии внешних деформаций <math>\varepsilon _{11}^0 = 0,\;{\rm{ }}\varepsilon _{22}^0 = 0</math> и при <math>{c_{{\rm{eq}}}} = {c_*}</math> реакция может идти только при: | ||
| + | <math> | ||
| + | \gamma > {\gamma _*} = \frac{{{E_ + }}}{{1 - {{\rm{\nu }}_ + }}}\varepsilon _{{\rm{ch}}}^2 | ||
| + | </math> | ||
| + | |||
| + | В этом случае выражение для коэффициента диффузии примет вид : | ||
| + | <math> | ||
| + | D = {D_0}{e^{\left( {\frac{{{E_ + }}}{{3(1 - \nu _ + )}}\left( {\varepsilon _{11}^0 + \varepsilon _{22}^0 - 2{\varepsilon _{{\rm{ch}}}}} \right)} \right){V_d}/kT}} | ||
| + | </math> | ||
| + | |||
| + | <math>D</math> не зависит от координаты <math>x_3</math>, поэтому уравнение диффузии примет вид: | ||
| + | <math> | ||
| + | {\rm{\Delta }}c = 0\;\quad \Rightarrow \quad \frac{{{\partial ^2}c}}{{\partial x_3^2}} = 0 | ||
| + | </math> | ||
| + | Решением этого уравнения будет линейная функция <math>c = A{x_3} + B</math>. Из граничных условий можно найти константы <math>A</math> и <math>B</math>. В итоге, функция концентрации будет выглядеть следующим образом: | ||
| + | <math> | ||
| + | c = \;\frac{{D\alpha {c_*} + {n_*}^2{k_*}\alpha h{c_*} - D{n_*}^2{k_*}{c_{{\rm{eq}}}} - \alpha {n_*}^2{k_*}\left( {{c_*} - {c_{{\rm{eq}}}}} \right){x_3}}}{{\left( {D\alpha + {n_*}^2{k_*}\alpha h - D{n_*}^2{k_*}} \right)}} | ||
| + | </math> | ||
| − | + | Подставляя полученное выражение в уравнение для скорости распространения реакции, окончательно получим: | |
| + | <math> | ||
| + | V = \frac{{{n_ - }{M_ - }{n_*}{k_*}D\alpha {c_*}(1 - \frac{{{c_{{\rm{eq}}}}}}{{{c_*}}})}}{{{\rho _ - }\left( {D\alpha + {n_*}^2{k_*}\alpha h - D{n_*}^2{k_*}} \right)}} | ||
| + | </math> | ||
| + | В случае заданных усилий на поверхности можно найти напряжения <math>\sigma _{11}^0,\sigma _{22}^0</math>, отвечающие условиям баланса сил и моментов: | ||
| + | <math> | ||
| + | \int\limits_0^H {\sigma _{11}^0} d{x_3} = \int\limits_0^h {{{\left. {\sigma _{11}^ + } \right|}_{{x_1} = {l_1}}}} d{x_3} + \int\limits_h^H {{{\left. {\sigma _{11}^ - } \right|}_{{x_1} = {l_1}}}} d{x_3}, \nonumber\\\int\limits_0^H {\sigma _{22}^0} d{x_3} = \int\limits_0^h {{{\left. {\sigma _{22}^ + } \right|}_{{x_2} = {l_2}}}} d{x_3} + \int\limits_h^H {{{\left. {\sigma _{22}^ - } \right|}_{{x_2} = {l_2}}}} d{x_3}\nonumber\\ | ||
| + | \int\limits_0^H {{x_3}\sigma _{11}^0} d{x_3} = \int\limits_0^h {{{\left. {{x_3}\sigma _{11}^ + } \right|}_{{x_1} = {l_1}}}} d{x_3} + \int\limits_h^H {{{\left. {{x_3}\sigma _{11}^ - } \right|}_{{x_1} = {l_1}}}} d{x_3}, \nonumber\\\int\limits_0^H {{x_3}\sigma _{22}^0} d{x_3} = \int\limits_0^h {{{\left. {{x_3}\sigma _{22}^ + } \right|}_{{x_2} = {l_2}}}} d{x_3} + \int\limits_h^H {{{\left. {{x_3}\sigma _{22}^ - } \right|}_{{x_2} = {l_2}}}} d{x_3} | ||
| + | </math> | ||
| + | |||
| + | Чтобы найти напряжения из закона Гука, сделаем предположение, что <math>\varepsilon _{11}^{{\raise0.5ex\hbox{$\scriptstyle + $} | ||
| + | \kern-0.1em/\kern-0.15em | ||
| + | \lower0.25ex\hbox{$\scriptstyle - $}}} = A_1^{{\raise0.5ex\hbox{$\scriptstyle + $} | ||
| + | \kern-0.1em/\kern-0.15em | ||
| + | \lower0.25ex\hbox{$\scriptstyle - $}}}{x_3} + B_1^{{\raise0.5ex\hbox{$\scriptstyle + $} | ||
| + | \kern-0.1em/\kern-0.15em | ||
| + | \lower0.25ex\hbox{$\scriptstyle - $}}}, {\rm{ }}\varepsilon _{22}^{{\raise0.5ex\hbox{$\scriptstyle + $} | ||
| + | \kern-0.1em/\kern-0.15em | ||
| + | \lower0.25ex\hbox{$\scriptstyle - $}}} = A_2^{{\raise0.5ex\hbox{$\scriptstyle + $} | ||
| + | \kern-0.1em/\kern-0.15em | ||
| + | \lower0.25ex\hbox{$\scriptstyle - $}}}{x_3} + B_2^{{\raise0.5ex\hbox{$\scriptstyle + $} | ||
| + | \kern-0.1em/\kern-0.15em | ||
| + | \lower0.25ex\hbox{$\scriptstyle - $}}}</math>, и что <math> | ||
| + | \sigma_{33}=0</math>. | ||
| + | |||
| + | Из-за условий неразрывности мы получим, что <math>A_{1,2}^ + = A_{1,2}^ - = {A_{1,2}},{\rm{ }}B_{1,2}^ + = B_{1,2}^ - = {B_{1,2}}</math>. В этом случае напряжения будут выглядеть следующим образом: | ||
| + | |||
| + | <math> | ||
| + | \sigma _{11}^ - = \frac{{{E_ - }}}{{1 - {\rm{\nu }}_ - ^2}}\left( {\left( {{A_1} + {\rm{\nu }}_ - {A_2}} \right){x_3} + {B_1} + {\rm{\nu }}_ - {B_2}} \right)\nonumber\\ | ||
| + | \sigma _{22}^ - = \frac{{{E_ - }}}{{1 - {\rm{\nu }}_ - ^2}}\left( {\left( {{\rm{\nu }}_ - {A_1} + {A_2}} \right){x_3} + {\rm{\nu }}_ - {B_1} + {B_2}} \right)\nonumber\\ | ||
| + | \sigma _{11}^ + = \frac{{{E_ + }}}{{1 - {\rm{\nu }}_ + ^2}}\left( {\left( {{A_1} + {\rm{\nu }}_ + {A_2}} \right){x_3} + {B_1} + {\rm{\nu }}_ + {B_2}} \right) - \frac{{{E_ + }}}{{1 - {\rm{\nu }}_ + ^{}}}{\varepsilon _{{\rm{ch}}}}\nonumber\\ | ||
| + | \sigma _{11}^ + = \frac{{{E_ + }}}{{1 - {\rm{\nu }}_ + ^2}}\left( {\left( {{\rm{\nu }}_ + {A_1} + {A_2}} \right){x_3} + {\rm{\nu }}_ + {B_1} + {B_2}} \right) - \frac{{{E_ + }}}{{1 - {\rm{\nu }}_ + }}{\varepsilon _{{\rm{ch}}}} | ||
| + | </math> | ||
| + | |||
| + | Константы <math>A_1, A_2, B_1, B_2</math> можно найти из уравнений баланса. Функцию напряжений можно найти, заменив <math>\varepsilon_{11}</math> и <math>\varepsilon_{22}</math> на <math>\varepsilon _{11} = A_1{x_3} + B_1,{\rm{ }}\varepsilon _{22} = A_2{x_3} + B_2</math> соответственно. | ||
| + | При постоянном коэффициенте диффузии, проводя вычисления, аналогичные предыдущему пункту, получим, что <math>V\sim(1-\frac{c_{\rm{eq}}}{c_*})</math>. | ||
| + | Если коэффициент диффузии зависит от напряжений, то в данном случае он принимает следующий вид: | ||
| + | |||
| + | <math> | ||
| + | D = {D_0}{{\rm{e}}^{\left( {\frac{{{E_ + }}}{{3(1 - {{\rm{\nu }}_ + })}}\left( {\left( {{A_1} + {A_2}} \right){x_3} + \left( {{B_1} + {B_2} - 2{\varepsilon _{{\rm{ch}}}}} \right)} \right)} \right){V_d}/kT}} \Rightarrow D = {D_0}{{\rm{e}}^{\widetilde A{x_3} + \widetilde B}} | ||
| + | </math> | ||
| + | |||
| + | Тогда задача диффузии запишется следующим образом: | ||
| + | |||
| + | <math> | ||
| + | \frac{\partial }{{\partial {x_3}}}\left( {{D_0}{e^{\widetilde A{x_3} + \widetilde B}}\frac{{\partial c}}{{\partial {x_3}}}} \right) = 0\;\quad \Rightarrow \quad \frac{{{{\rm{d}}^2}c}}{{{\rm{d}}{x_3}^2}} + \widetilde A\frac{{{\rm{d}}c}}{{{\rm{d}}{x_3}}} = 0 | ||
| + | </math> | ||
| + | |||
| + | Решением этого уравнения будет функция <math>c = {c_1}{e^{ - \widetilde A{x_3}}} + {c_2}</math>, с граничными условиями, которые будут выглядеть как: | ||
| + | |||
| + | <math> | ||
| + | - {D_0}{e^{\widetilde B}}\widetilde A{c_1} + \alpha ({c_*} - {c_1} - {c_2}) = 0,\qquad - {D_0}{e^{\widetilde B}}\widetilde A{c_1} + {n_*}^2{k_*}({c_1}{e^{ - \widetilde Ah}} + {c_2} - {c_{{\rm{eq}}}}) = 0 | ||
| + | </math> | ||
| + | |||
| + | Окончательно, концентрация будет выглядеть следующим образом: | ||
| + | |||
| + | <math> | ||
| + | c = \frac{{\alpha {c_*}{n_*}^2{k_*}(1 - \frac{{{c_{{\rm{eq}}}}}}{{{c_*}}}){e^{ - \widetilde A{x_3}}} + {D_0}{e^{\widetilde B}}\widetilde A{c_*}\left( {\alpha + {n_*}^2{k_*}\frac{{{c_{{\rm{eq}}}}}}{{{c_*}}}} \right) + \alpha {n_*}^2{k_*}{c_*}(\frac{{{c_{{\rm{eq}}}}}}{{{c_*}}} - {e^{ - \widetilde Ah}})}}{{{D_0}{e^{\widetilde B}}\widetilde A\left( {\alpha + {n_*}^2{k_*}} \right) + \alpha {n_*}^2{k_*}(1 - {e^{ - \widetilde Ah}})}} | ||
| + | </math> | ||
| + | |||
| + | Скорость в этом случае запишется согласно следующей формуле: | ||
| + | |||
| + | <math> | ||
| + | V = \frac{{{n_ - }{M_ - }}}{{{\rho _ - }}}\frac{{{D_0}{e^{\widetilde B}}\widetilde A\alpha {c_*}{k_*}{n_*}\left( {1 - \frac{{{c_{{\rm{eq}}}}}}{{{c_*}}}} \right)}}{{{D_0}{e^{\widetilde B}}\widetilde A\left( {\alpha + {n_*}^2{k_*}} \right) + \alpha {n_*}^2{k_*}(1 - {e^{ - \widetilde Ah}})}} | ||
| + | </math> | ||
== Результаты == | == Результаты == | ||
== Список литературы == | == Список литературы == | ||
| + | 1) Freidin, A.B., Vilchevskaya, E. N., Korolev, I. K.: Stress-assist chemical reactions front propagation in deformable solids. International Journal of Engineering Science, 83 (2014), pp. 57-75. | ||
| + | |||
| + | 2) Prigogine, I., Defay, R.: Chemical thermodynamics. London: Longmans, Green, 1954. | ||
| + | |||
| + | 3) Thermodynamic theory of structure, stability and fluctuation. Wiley Interscience, London, 1971, pg. 50. | ||
| + | |||
| + | 4) Ming-Tzer Lin.: Stress effects and oxidant diffusion in the planar oxidation. (1999). Thesis and Dissertation, Lehigh University. Paper 594 | ||
| + | |||
| + | 5) B.E.Deal, A.S. Grove: General relationship for the thermal oxisation of Silicon. Journal of Applied Physics, vol.36(12), December 1965. | ||
Текущая версия на 15:13, 1 декабря 2015
БАКАЛАВРСКАЯ РАБОТА
Автор работы: Григорьева Полина
Научный руководитель: Елена Вильчевская
Содержание
Введение[править]
Проблема термического окисления кремния сегодня является одной из важнейших проблем в химии в связи с широким использованием и значимостью технологии кремниевых интегральных схем. Так как объем молекулы диоксида кремния примерно в 2.3 раза больше атома кремния, окисление кремния сопровождается большим увеличением объема. Это значит, что эта проблема принадлежит области механохимии, которая рассматривает химические реакции под действием механических нагрузок. В этой работе будет изучен простейший аналитический пример, позволяющий понять основные идеи, в котором фронт химической реакции распространяется вдоль одной оси и остается плоским внутри всего трехмерного тела. Несмотря на то, что значения для некоторых численных вычислений были взяты из параметров для , и , полученные теоретические результаты можно использовать для реакций этого типа. Кроме того, базируясь на результатах предшествовавшей работы (1), была решена задача диффузии и были приведены результаты с учетом коэффициента диффузии, зависящего от механических нагрузок.
Цели[править]
- Исследовать кинетику химического фронта в трехмерном линейно-упругом теле с плоским химическим фронтом под влиянием механических нагрузок;
- Исследовать влияние зависимости коэффициента диффузии от напряжений.
Постановка задачи: Модель и уравнения[править]
Теория кинетики химических реакций основана на концепции химических потенциалов и химического сродства, которые являются линейной комбинацией химических потенциалов веществ, принимающих участие в реакции. В классической теории химический потенциал является скаляром. Однако этот подход действителен только для газов и жидкостей, но редко для твердых тел. Если мы хотим исследовать фазовый переход в деформируемых твердых материалах, нам нужно тензорное выражение для химического потенциала. Это также значит, что химическое сродство тоже станет тензором. В связи с проблемой, описанной в предыдущем разделе, мы рассмотрим химическую реакцию между твердой и газовой компонентами:
где и относятся к деформируемым твердым компонентам, а - к газовой компоненте. Мы считаем, что реакция сконцентрирована около фронта реакции, , который разделяет области, занятые и . Реакция проистекает и продолжается вследствие диффузии газовой компоненты сквозь образующуюся . Мы считаем, что весь газ, подходящий к фронту, будет израсходован в химической реакции. Как пример такой реакции, мы можем рассмотреть уравнение, описывающее образование диоксида кремния .
Мы считаем, что область, занятая , является проницаемой для газовой компоненты, которая может свободно диффузировать через твердую компоненту и не вызывать в ней никаких деформаций. Для простоты мы не учитываем эффекты внутреннего трения, влияние реакции на температуру, т.е. мы не реашем задачу теплопроводности, и считаем температуру параметром модели.
Было показано, что нормальная компонента тензора химического сродства может быть вычислена согласно следующей формуле (см.(1)):
где и - тензора напряжений Коши, являются тензорами жесткости упругих компонент, - тензора деформации, - концентрация газа на фронте реакции, - растворимость газовой компоненты в сформированном материале . Также мы относим деформации химических превращений к и считаем, что эти деформации изотропны в объеме, т.е. , где - единичный тензор. Параметр отвечает за отсчетные уровни химических энергий. Если температура дана, является параметром модели (более подробно см. (2), (3)).
Если мы заменим скалярную величину химического сродства нормальной компонентой тензора химического сродства, скорость на элементе поверхности с нормалью будет определяться выражением:
где - скорость прямой химической реакции, является кинетической константой скорости химической реакции. Тогда из баланса массы на фронте реакции, , - нормальная компонента скорости распространения химического фронта, следует, что :
Фронт реакции продвигается, только если . Тогда из уравнения мы можем найти равновесную концентрацию на фронте реакции:
Вводя эту равновесную концентрацию, мы можем переписать вблизи химического равновесия как . Следовательно, мы можем переписать и формулу для скорости распространения реакции:
Концентрация газовой компоненты на фронте химической реакции может быть найденa из второго закона Фика для диффузии:
Мы считаем, что процесс диффузии не зависит от времени. Тогда уравнение принимает вид:
Граничными условиями являются:
Первое условие следует из условия баланса массы на внешней границе тела , - константа скорости растворения молекул газа в новом материале. Второе условие следует из условия баланса массы на фронте реакции . Определение коэффициента диффузии используется согласно (4). Коэффициент диффузии может быть подсчитан по следующей формуле: где за обозначено давление на фронте реакции, - температура системы, - объем, занимаемый молекулой, и - температурная постоянная Больцмана. Кроме того, величина , варьируется от 1.1 до 2 в зависимости от температуры. Итак, задача сводится к следующим пунктам: сначала мы находим . Далее, мы находим из задачи диффузии и затем, окончательно, подставляем полученные значения в формулу для нормальной компоненты скорости.
Решение для различных видов механических нагрузок[править]
В этом разделе мы представим аналитическое решение задачи для простейшей геометрии. Станем рассматривать трехмерный прямоугольный параллелепипед: с реакцией, распространяющейся в направлении оси и фронтом реакции, представленным плоскостью . Считаем, что концентрация не зависит от координат и , поэтому , .
Будет изучено два случая механической нагрузки:
первый, перемещения на поверхности тела заданы, и второй, напряжения на поверхности заданы.
Считаем, что нам даны перемещения, которые приложены к телу следующим образом:
Тогда деформации равномерно распределены по всему телу:
Сдвиговые деформации отсутствуют, т.е. .
Считаем, что напряжения по оси отсутствуют, т.е. имеем дело с плосконапряженной задачей. Тогда из закона Гука можем вычислить оставшиеся напряжения и деформации:
Для региона "+":
Для удобства расчетов с значениями параметров конкретного материала перейдем к модулю Юнга, , и коэффициенту Пуассона, , и запишем выражение для функции напряжений, входящей в состав выражения для вычисления :
Реакция идет только при . Следовательно, при отсутствии внешних деформаций и при реакция может идти только при:
В этом случае выражение для коэффициента диффузии примет вид :
не зависит от координаты , поэтому уравнение диффузии примет вид:
Решением этого уравнения будет линейная функция . Из граничных условий можно найти константы и . В итоге, функция концентрации будет выглядеть следующим образом:
Подставляя полученное выражение в уравнение для скорости распространения реакции, окончательно получим:
В случае заданных усилий на поверхности можно найти напряжения , отвечающие условиям баланса сил и моментов:
Чтобы найти напряжения из закона Гука, сделаем предположение, что , и что .
Из-за условий неразрывности мы получим, что . В этом случае напряжения будут выглядеть следующим образом:
Константы можно найти из уравнений баланса. Функцию напряжений можно найти, заменив и на соответственно. При постоянном коэффициенте диффузии, проводя вычисления, аналогичные предыдущему пункту, получим, что . Если коэффициент диффузии зависит от напряжений, то в данном случае он принимает следующий вид:
Тогда задача диффузии запишется следующим образом:
Решением этого уравнения будет функция , с граничными условиями, которые будут выглядеть как:
Окончательно, концентрация будет выглядеть следующим образом:
Скорость в этом случае запишется согласно следующей формуле:
Результаты[править]
Список литературы[править]
1) Freidin, A.B., Vilchevskaya, E. N., Korolev, I. K.: Stress-assist chemical reactions front propagation in deformable solids. International Journal of Engineering Science, 83 (2014), pp. 57-75.
2) Prigogine, I., Defay, R.: Chemical thermodynamics. London: Longmans, Green, 1954.
3) Thermodynamic theory of structure, stability and fluctuation. Wiley Interscience, London, 1971, pg. 50.
4) Ming-Tzer Lin.: Stress effects and oxidant diffusion in the planar oxidation. (1999). Thesis and Dissertation, Lehigh University. Paper 594
5) B.E.Deal, A.S. Grove: General relationship for the thermal oxisation of Silicon. Journal of Applied Physics, vol.36(12), December 1965.