Вязкоупругая модель склеральной оболочки глаза — различия между версиями

Версия 22:02, 16 июня 2016

МАГИСТЕРСКАЯ РАБОТА
Автор работы: К.П. Фролова
Научный руководитель: к.ф-м.н., доцент Е.Н. Вильчевская

Введение и мотивация работы

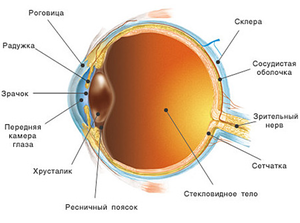
При построении простейших моделей глаза можно считать, что он имеет шаровидную форму. Глаз заполнен прозрачной гелеобразной субстанцией, называемой стекловидным телом. Во внешней фиброзной оболочке глаза можно выделить наружную фиброзную, среднюю сосудистую и внутреннюю сетчатую оболочки. Наружная фиброзная (корнеосклеральная) оболочка глаза выполняет защитную функцию и обуславливает форму глаза. Она состоит из передней прозрачной части - роговицы, - и задней непрозрачной части – склеры, обладающих различными радиусами кривизны и биомеханическими характеристиками. Склера занимает 93% внешней фиброзной оболочки глаза человека, поэтому в задачах, связанных с определением формы и изменением объема глазного яблока под действием внутриглазного давления (ВГД), биомеханические свойства склеры играют решающую роль, и поведение глаза допустимо моделировать поведением его склеральной оболочки.

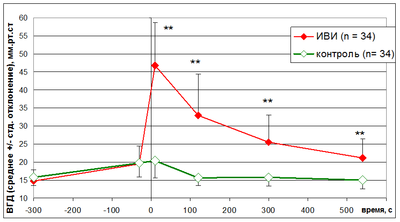
На экспериментальных кривых, соответствующих изменению ВГД в течение нескольких минут после введения интравитреальной инъекции - инъекции внутрь стекловидного тела, - наблюдается его резкий скачок непосредственно после инъекции, вызванный увеличением объема, а затем спад до некоторого постоянного значения. В большинстве существующих источников литературы данный спад объясняется наличием оттока внутриглазной жидкости из нагруженного глаза. В связи с уменьшением объема происходит уменьшение ВГД. Однако известно, что склере присуща вязкоупругая реакция на приложенную нагрузку. Непосредственное измерение вязкости склеры вызывает технические сложности и, в связи с этим, в литературе отсутствуют сведения о соответствующих параметрах вязкости. Это приводит к тому, что в большинстве существующих моделей вязкие свойства склеры игнорируются, а поведение склеры при нагрузках предполагается чисто упругим. В данной работе релаксация напряжений (спад ВГД) в глазу после введения интравитреальной инъекции объясняется не только наличием оттока внутриглазной жидкости из нагруженного глаза, но и вязкими свойствами склеральной оболочки глаза. В рамках данной работы будет предложен метод определения коэффициента сдвиговой вязкости склеры, заключающийся сравнении результатов математического моделирования и указанных в литературе экспериментальных данных, основанных на дискретном измерении ВГД в течение нескольких минут после интравитреальной инъекции. Будут рассмотрены различные варианты постановки граничных условий. В первом случае будет предполагаться, что введенный при инъекции дополнительный объем жидкости сохраняется в стекловидном теле на протяжении времени проведения эксперимента, релаксация напряжений будет объясняться только наличием вязких свойств склеры. Во втором случае будет учитываться отток внутриглазной жидкости, релаксация напряжений будет объясняться наличием обоих факторов: и наличием вязких свойств склеры, и наличием оттока внутриглазной жидкости из нагруженного глаза. Будет определяться значение коэффициента сдвиговой вязкости, при котором отклонение теоретических данных от экспериментальных минимально.

Цели исследования

• Смоделировать вязкоупругое поведение склеры после интравитреальной инъекции — инъекции внутрь стекловидного тела;
• Определить значение коэффициента сдвиговой вязкости склеры путем сравнения результатов математического моделирования и указанных в литературе экспериментальных данных, основанных на дискретном измерении внутриглазного давления (ВГД) в течение нескольких минут после интравитреальной инъекции.

Постановка задачи

Моделируемый в рамках данной работы эксперимент основан на дискретном измерении ВГД в течение нескольких минут после введения интравитреальной инъекции в объеме 0,05 мл. Точки на экспериментальной кривой соответствуют средним значениям ВГД для 34 пациентов. Для контроля состояния пациентов ВГД измерялось также и на парном не вакцинированном глазу. Задача моделируется вязкоупругим сферическим слоем с внутренним радиусом [math]R_1[/math] и внешним радиусом [math]R_2[/math] при центральносимметричной нагрузке: внешнее давление отсутствует, на внутреннем радиусе заданы перемещения, учитывающие величину дополнительного объема жидкости, введенного при инъекции. Задание нулевого давления на внешнем радиусе объясняется тем, что по определению ВГД есть разница между атмосферным давлением и давлением в глазу. Материал склеры предполагается линейным трансверсально – изотропным. Задача решается в рамках трехмерной теории линейной вязкоупругости.

Материалы и методы

Математическая модель
Система уравнений
Рассматриваемая задача является квазистатической, следовательно, уравнение движения сферического слоя сводится к уравнению равновесия:
[math]\nabla \cdot {\pmb{\sigma }} = 0,[/math]
где [math]\pmb{\sigma }[/math] - тензор напряжений. В силу симметрии задачи данное уравнение в координатном виде в сферической системе координат сводится к следующему:
[math]\dfrac{{\partial {\sigma _{rr}}}}{{\partial r}} + 2\dfrac{{{\sigma _{rr}} - {\sigma _{\varphi \varphi }}}}{r} = 0[/math]
Для получения определяющих соотношений воспользуемся реологической моделью Кельвина – Фойгта, достаточно хорошо описывающей поведение вязкоупругих твердых тел. Данная модель предполагает суммирование упругих и вязких напряжений и равенство упругих и вязких деформаций в теле. При этом для получения единственного решения задачи нам необходимо включать в уравнения лишь один неизвестный параметр вязкости. Итак, определяющие соотношения:
[math]{\pmb{\sigma }} ={{}^4}{\pmb{C}}:{\pmb{\varepsilon }}+ 2\eta {\pmb{\dot e}},[/math]
где [math]{{}^4}{\pmb{C}}[/math] - тензор жесткости четвертого ранга, [math]\eta[/math] - коэффициент сдвиговой вязкости, [math]\pmb{e}[/math] - девиавтор тензора деформаций.
Ненулевые компоненты тензора деформаций связаны с перемещениями следующим образом:
[math]{\varepsilon _{rr}} = \dfrac{{d{u_r}}}{{dr}}\;,\;\; {\varepsilon _{\varphi \varphi }} = {\varepsilon _{\theta \theta }} = \dfrac{{{u_r}}}{r}.[/math]
Безразмерная постановка задачи
Задача решается в безразмерной постановке. Введем следующие безразмерные параметры:
безразмерную координату по радиусу [math]\beta = \dfrac{{{R_1}}}{{{R_2}}} \le x = \dfrac{r}{{{R_2}}} \le 1[/math], безразмерное перемещение [math]u = \dfrac{{{u_r}}}{{{R_2}}}[/math], безразмерную компоненту тензора напряжений [math]{\sigma _{ij\dim }} = \dfrac{{{\sigma _{ij}}}}{{{E_{\theta \theta }}}}[/math], безразмерный модуль Юнга [math]\xi = \dfrac{{{E_{rr}}}}{{{E_{\theta \theta }}}}[/math] и безразмерное время [math]\tau = \dfrac{{{E_{\theta \theta }}}}{\eta }t.[/math]
Тогда уравнение равновесия в перемещениях в безразмерном виде примет следующий вид:
[math]\dfrac{{{\xi ^2}(1 - {\nu _{\theta \varphi }})}}{{\xi (1 - {\nu _{\theta \varphi }}) - 2\nu _{r\theta }^2}}\left[ {\dfrac{{{\partial ^2}u}}{{\partial {x^2}}} + \dfrac{2}{x}\dfrac{{\partial u}}{{\partial x}} - \dfrac{{2(1 - {\nu _{r\theta }})}}{{\xi (1 - {\nu _{\theta \varphi }})}}\dfrac{u}{{{x^2}}}} \right] + \dfrac{4}{3}\left[ {\dfrac{{{\partial ^2}\dot u}}{{\partial {x^2}}} + \dfrac{2}{x}\dfrac{{\partial \dot u}}{{\partial x}} - 2\dfrac{{\dot u}}{{{x^2}}}} \right] = 0.[/math]
ВГД может быть определено как радиальное напряжение на внутренней границе сферического слоя, взятое с обратным знаком, поскольку внешняя нормаль к внутренней границе тела направлена вовнутрь, а ВГД стремится увеличить объем тела. Итак, безразмерное ВГД определяется следующей формулой: [math]IO{P_{\dim}}(\tau) = {\left. { - {\sigma _{xx}}}(\tau) \right|_{x = \beta }}.[/math]
Безразмерное радиальное напряжение как функция перемещений:
[math]{\sigma _{xx}} (\tau) = \dfrac{{2{\nu _{r\theta }}\xi }}{{\xi (1 - {\nu _{\theta \varphi }}) - 2\nu _{r\theta }^2}}\dfrac{u}{x} + \dfrac{{(1 - {\nu _{\theta \varphi }}){\xi ^2}}}{{\xi (1 - {\nu _{\theta \varphi }}) - 2\nu _{r\theta }^2}}\dfrac{{\partial u}}{{\partial x}} + \dfrac{4}{3}\left[ {\dfrac{{\partial{\dot u}}}{{\partial x}} - \dfrac{{\dot u}}{x}} \right].[/math]
Граничные условия
В рамках данной работы используются два типа граничного условия на внутреннем радиусе. В первом случае предполагается, что объем глазного яблока, включающий в себя дополнительный объем жидкости [math]{\Delta V}[/math], введенный при инъекции внутрь стекловидного тела, и объем глазного яблока [math]V_0^{eye}[/math] до нагружения, сохраняется на протяжении времени проведения эксперимента. При этом напоминаем, что моделирование глазного яблока сводится к моделированию склеральной оболочки глаза. Граничные условия задаются следующим образом:
[math]{\sigma _{xx}}(\tau )\left| {_{x = 1}} \right. = 0\;,\;\; u(\tau )\left| {_{x = \beta }} \right. = {u_0}H(\tau ),[/math]
где [math]{u_0} \approx \dfrac{{\Delta V}}{{4\pi {R_2}R_1^2}}[/math], [math]H(\tau)[/math] - единичная степенная функция Хевисайда.
Во втором типе граничного условия на внутреннем радиусе учитывается гидродинамика внутриглазной жидкости, в частности, более интенсивный отток внутриглазной жидкости из нагруженного глаза. Для определения величины изменения объема глазного яблока, обусловленного притоком и оттоком внутриглазной жидкости, обратимся к методу тонографии. Данный метод оперирует скоростью изменения объема глазного яблока. Текущий объем глаза определяется следующим образом:
[math]V(t) = V(0)+\int\limits_{\tilde t = 0}^{\tilde t = t} {\dot V(\tilde t)d\tilde t} = V_0^{eye} + \Delta V + \int\limits_{\tilde t = 0}^{\tilde t = t} {\dot V(\tilde t)d\tilde t}.[/math]
Изменение объема глаза, вызванное гидродинамикой внутриглазной жидкости: [math]V(t) - V(0) = V(t) - V_0^{eye} - \Delta V = 4\pi R_{inj}^2{u_r}(t),[/math] где [math]{R_{inj}} = \sqrt[3]{{R_1^3 + \dfrac{{3\Delta V}}{{4\pi }}}}.[/math] Граничные условия задаются следующим образом:
[math]{\sigma _{xx}}\left( t \right)\left| {_{x = 1}} \right. = 0,u\left( t \right)\left| {_{x = \beta }} \right. = {u_0} + \dfrac{{\int\limits_{\tilde t = 0}^{\tilde t = t} {\dot V\left( {\tilde t} \right)d\tilde t} }}{{4\pi {R_2}R_{inj}^2}}[/math]
Дальнейшее использование безразмерного времени затруднительно, поскольку в граничном условии на внутреннем радиусе присутствует интеграл по времени. Для определения величины [math]\int_{\tilde t = 0}^{\tilde t = t} {\dot V(\tilde t)d\tilde t}[/math] воспользуемся данными тонографии - метода измерения и регистрации ВГД, позволяющего определить интенсивность оттока внутриглазной жидкости. В рамках данного метода предполагается, что скорость изменения объема глазного яблока зависит от скоростей притока и оттока внутриглазной жидкости. При этом получается, что интересующий нас интеграл определяется следующим образом:
[math]\int\limits_{\tilde t = 0}^{\tilde t = t} {\dot V\left( {\tilde t} \right)d\tilde t} = \int\limits_{\tilde t = 0}^{\tilde t = t} {\left( {F\left( {\tilde t} \right) - R\left( {\tilde t} \right)} \right)d\tilde t},[/math]
где [math]F, R[/math] - скорости притока и оттока внутриглазной жидкости соответственно.
Величина оттока жидкости определяется следующим гидравлическим соотношением: [math]R = C\left( {P - {P_e}} \right),[/math] где [math]C[/math] - коэффициент легкости оттока внутриглазной жидкости, [math]P[/math] - аппроксимирующая функция ВГД, [math]{P_e}[/math] - давление в эписклеральных венах. Основная задача тонографии состоит в том, чтобы оценить величину коэффициента легкости оттока. При стандартной обработке данных тонографии данная величина оценивается на основе представления тонограммы линейной функцией, причем для обработки используются только начальная и конечная точки тонограммы. В работе Г. Любимова предложен модифицированный алгоритм обработки данных тонографического исследования, предусматривающий оценку тонографической кривой, основанную на использовании не только начального и конечного значений ВГД, но и его промежуточных значений. При этом рассматривается несколько схем обработки данных тонографии. При стандартной схеме делаются следующие предположения: [math]{P_e} - {P_{e0}} = 1.25[/math], [math]C = {C_0} = const[/math], [math]F = {F_0} = const, [/math] где индекс "0" соответствует параметрам в ненагруженном состоянии.
При 1-ой модифицированной схеме делаются следующие предположения: [math]{P_e} - {P_{e0}} = 1.25[/math], при этом [math]F = {R_{st}} \ne {F_0}[/math]. При 2-ой модифицированной схеме делаются следующие предположения: [math]F = {R_{st}} = {F_0}[/math], при этом [math]{P_e} - {P_{e0}} \ne 1.25[/math].
Прямое и обратное преобразования Лапласа
Для получения решения для перемещений и радиальных напряжений воспользуемся методом преобразования Лапласа, связывающим функцию [math]f\left( {x,\tau } \right)[/math] действительного переменного (оригинал), с функцией [math]\[\bar f\left( {x,s} \right)\][/math] комплексного переменного (изображением). Изображение функции - оригинала по Лапласу определяется следующим выражением:
[math]\bar f\left( {x,s} \right) = \exp \left( { - s\tau } \right)f\left( {x,\tau } \right)d\tau,[/math]
где [math]s[/math] - комплексная переменная, [math]s = c + i\omega ,c \gt {s_0}[/math].

Результаты исследования

Выводы

При учете обоих факторов: наличия вязкости склеральной оболочки глаза и интенсивного оттока внутриглазной жидкости из нагруженного глаза, - теория лучше согласуется с экспериментом, чем при учете одного из них. Таким образом, релаксацию напряжений невозможно описать качественно наличием только лишь вязкоупругого поведения склеры при нагружении или наличием гидродинамики внутриглазной жидкости. При этом оказалось, что значение коэффициента сдвиговой вязкости склеры меньше в случае предположения постоянства объема глаза на протяжении времени проведения эксперимента. Величина коэффициента сдвиговой вязкости влияет на характер релаксации напряжений: чем больше коэффициент сдвиговой вязкости, тем более продолжительна релаксация напряжений. Выбор численного алгоритма обратного преобразования Лапласа при рассмотрении алгоритма Закиана, а также алгоритмов Джеффресона и Чоу для 10-ти и 15-ти членов разложения ряда в квадратурной формуле, задающей численное обратное преобразование Лапласа, не оказывает значительного влияния на результат. При этом стоит отметить, что использование алгоритма Закиана наименее трудоемко с вычислительной точки зрения в силу использования наименьшего числа членов разложения ряда в квадратурной формуле. Традиционные предположения тонографии приводят к результатам, лучше согласующимся с экспериментальными данными, чем предположения модифицированных схем обработки данных тонографического исследования. Такой вывод может объясняться тем, что при попытке описать одни физические механизмы работы гидродинамической системы глаза необходимо параллельно учитывать ряд других процессов и факторов. Так, если принимать, что часть параметров, характеризующих состояние глаза, изменяется при нагружении глаза, вполне вероятно, что нужно учитывать сам характер нагружения и величину прикладываемой нагрузки. В рамках же рассматриваемой модели в работе Г. Любимова принято, что ряд параметров меняется при нагружении, но при этом не зависит явно от величины ВГД и приложенной нагрузки, т.е. меняется скачкообразно и затем сохраняется на протяжении времени проведения эксперимента. При этом предположение о том, что скорость притока внутриглазной жидкости меняется при нагружении, а давление в эписклеральных венах остается практически неизменным, приводит к меньшему значению коэффициента сдвиговой вязкости склеры и наблюдению меньшего спада ВГД с течением времени. Предположение о том, что приток жидкости не зависит от ВГД и величины нагрузки, тогда как давление в эписклеральных венах предполагается заметно отличным от соответствующего значения в ненагруженном глазу, приводит к наблюдению резкого спада ВГД с течением времении, что качественно не согласуется с экспериментальными данными. Найденные значения коэффициента сдвиговой вязкости в этом случае больше. Коэффициент сдвиговой вязкости склеры зависит от значений модулей Юнга в направлении оси симметрии и плоскости изотропии в трансверсально – изотропном материале. При допустимом варьировании значений модулей оказывается, что коэффициент сдвиговой вязкости тем больше, чем меньше модули Юнга. При этом использование комбинации модулей Юнга, предложенной в работах С.М. Бауэр, является наиболее удовлетворительной при сопоставлении теоретических данных с экспериментальными.

Список литературы

• D. Ljubimova. Biomechanics of the Human Eye and Intraocular Pressure Measurements // Ph.D. thesis - Royal Institute of Technology - 2009.
• Л.А. Карамшина. Модели многослойных оболочек в задачах офтальмологии // Дисс. – Санкт-Петербургский государственный университет - 2011.
• С.А. Регирер. Лекции по биологической механике – Изд. Московского университета – 1980 – 144 с.
• К. Котляр, С. Бауэр, Н. Планге. Клинические и биомеханические аспекты изменения внутриглазного давления после интравитреальных инъекций // Российский общенациональный офтальмологический форум - 2013.
• В. Новацкий. Теория упругости // Пер. с польского – М.: Мир - 1975 - 872 с.
• Р. Кристенсен. Введение в механику композитов // Пер. с англ. – М.: Мир - 1982 – 334 с.
• Е.Н. Иомдина, С.М. Бауэр, К.Е. Котляр. Биомеханика глаза: теоретические аспекты и клинические приложения // М.: Реал Тайм – 2015 – 208 с.
• Г.А. Любимов, И.Н. Моисеева, А.А. Штейн, Е.Н. Иомдина, Л.А. Назаренко. Об оценке величины оттока жидкости из глаза с помощью модифицированного метода тонографии // Российский журнал биомеханики – 2012 – Т.16 - №2 – сс. 8–20.
• Л.А. Игумнов, С.Ю. Литвинчук, А.А. Белов. Численное обращение преобразования Лапласа: Учебно – методическое пособие // Изд. Нижегородского университета – 2010 – 34 с.
• G. Doetsch. Introduction to the Theory and Application of the Laplace Transformation // Springer – 1974 - 327 p.
• J. Abate, W. Whitt. A Unified Framework for Numerically Inverting Laplace Transforms// INFORMS Journal on Computing – 2006 - V.18 - No.4 - pp.408-421.
• G. A. Baker, P. Graves-Morris. Pad´e Approximants, 2nd ed. // Cambridge University Press, Encyclopedia of Mathematics and Its Applications – 1996 - Vol.59 – 764 p.
• V. Zakian. Numerical inversion of Laplace transform // Elec. Lett. – 1969 - No.5 - pp.120-121.
• V. Zakian. Optimisation of numerical inversion of Laplace transforms // Elec. Lett. – 1970 - No.6 - pp.677-679.
• C.P. Jeffreson, E.-P. Chow. Least squares coefficients for a quadrature formula for Laplace transform inversion // Journal of Computational and Applied Mathematics – 1978 – V.4 - №1 - pp. 53-58.
• G. Miller. Least squares approximation of functions using exponentials // Ph.D. thesis - John Hopkins Univ. - 1969.
• С.М. Бауэр, Л.А. Замураев, К.Е. Котляр. Модель трансверсально-изотропного сферического слоя для расчета изменения внутриглазного давления при интрасклеральных инъекциях // Российский журнал биомеханики – 2010 – Т.10 - №2 – сс.43–49.
• Б.С. Першин. Гидродинамический баланс глазного яблока при интравитреальном введении дополнительного объема жидкости // Дисс. – ФГБУ Научно-исследовательский институт глазных болезней РАМН - 2012.
• C.H. Morales. A Bolzano’s theorem in the new millennium // Nonlinear Analysis – 2002 - No. 51 - pp. 679-691.
• Е.Н. Иомдина. Механические свойства тканей человека // Изд. МГУ: Современные проблемы биомеханики – 2006 – Вып.11 – сс.183-200.