Создание модели насыщения связи в простейших углеводородах

Проект выполняет Соколов Алексей

Аннотация

Метод молекулярной динамики широко используется в различных областях, включая физику, химию, биологию, для того чтобы достичь понимания молекулярных процессов недоступных в эксперименте. Несмотря на то, что наиболее точно описывает межмолекулярные взаимодействия квантовая механика, для практического применения этот метод требует недопустимо много вычислительных ресурсов. С другой стороны Гамильтониан механической системы может быть описан с помощью классических законов механики. В общем случае Гамильтониан состоит из кинетической и потенциальной энергии. Полная кинетическая энергия системы есть сумма всех кинетических энергий частиц. Потенциальная энергия напротив является сложной функцией, описывающей различные взаимодействия между частицами. Вообще говоря функция, описывающая силовое поле, содержит множество параметров, которые должны быть выбраны таким образом, чтобы Гамильтониан точно описывал интересующие нас свойства системы. Параметры системы могут быть выбраны на основании, данных полученных из квантовой механики и экспериментальных данных. Предлагается комбинированный подход основанный на методе молекулярной динамики, эмпирических представлениях квантовой механики и классических законах механики. Целью данного исследования является создание модели, позволяющей проводить компьютерное моделирование атомарных систем, состоящих из большого числа частиц, описывающей насыщение межатомной связи.

Файл:Presentation Sokolov.pptx

Введение

В последнее время компьютерное моделирование получило широкое распространение как мощный инструмент для описания физических явлений. Использование потенциалов и описание межатомных взаимодействий с помощью силовых полей получило широкое распространение для моделирования тел с микроструктурой. Подробное описание различных потенциалов и их применения для описания тел с микроструктурой приведено в работах . В зависимости от масштаба рассматриваемых явлений могут быть использованы различные компьютерные модели. Для описания систем на электронно ядерном уровне используется теория функционала плотности , метод Харти-Фока . Для моделирования протеинов, липидов и других органических соединений используется силовое поле GROMOS . Предложенный в 1976 году подход “QM/MM” в работе , комбинирующий точность квантово-механического описания и скорость вычислений молекулярной динамики, получил бурное развитие в последнее время и позволил проводить моделирование сложных химических соединений. За работу <<развитие моделей комплексных химических систем>>, в основе которой лежит подход “QM/MM”, Мартином Карплюсом, Майклом Левиттом и Ари Уоршелом в 2013 была получена Нобелевская премия . Потенциал погруженного атома (embedded atom model, EAM) основанный на теории приближения сильной связи, известной также как модель Финниса-Синклера , используется для описания межатомных взаимодейсвий между ионами и окружающего их электронного газа в металлах . Один из самых простых парных потенциалов, потенциал Леннарда-Джонса используется для описания слабых Ван дер Вальсовских взаимодействий сферических неполярных молекул, например в инертных газах. Метод молекулярной динамики стал активно разрабатываться в 50-х годах XX-го столетия Б. Альдером и получил широкое развитие. Метод молекулярной динамики позволяет описывать большие атомарные системы (например состоящие из [math]10^9[/math] частиц) с помощью решения уравнений динамики Ньютона в 3-х мерном пространстве и позволяет предсказать явления, которые невозможно описать с помощью аналитического подхода или эксперимента. Возможность воспроизведения эксперимента сделало этот метод особенно популярным в последнее время. Исследователь имеет возможность изменять начальные условия и наблюдать влияние этих изменений на конечный результат, что не всегда возможно в условиях реального эксперимента. систему на электронно-ядерном уровне можно с помощью уравнения Шредингера ([eq:Shrod]) . [math]\label{eq:Shrod} \hat{H} \Psi = E \Psi,[/math] [math]\label{eq:Shrodinger} \left[T_N + T_e + V_{ee}(r) + V_{NN}(R) + V_{eN}(r,R) \right] \Psi = E \Psi,[/math] где [math]T_N[/math] — кинетическая энергия ядра, [math]T_e[/math] — кинетическая энергия электронов, [math]V_{NN}[/math] — ядерно-ядерное взаимодействие, [math]V_{eN}[/math] — электронно ядерное взаимодействие и [math]V_{ee}[/math] — электрон-электронное взаимодействие.

Волновая функция для системы фермионов может быть записана как функция построенная из одночастичных функций через определитель Слэтера : [math]\begin{aligned} \Psi = \frac{1}{\sqrt{N!}} \begin{vmatrix} \psi_1( \mathbf{r}_1) & \cdots & \psi_1( \mathbf{r}_N) \\ \vdots& &\vdots \\ \psi_N( \mathbf{r}_1) & \cdots & \psi_N( \mathbf{r}_N) \\ \end{vmatrix}.\end{aligned}[/math]

Масса ядра значительно превышает массу электрона, вследствие чего скорость движения ядер мала по отношению к скорости движения электронов. В результате медленно движущиеся ядра образуют электростатическое поле, в котором с намного большей скоростью движутся электроны, успевающие мгновенно подстроиться к любому изменению координат ядер. Поэтому в приближении считают ядра фиксированными и рассматривают только движение электронов. На языке квантовой механики это эквивалентно допущению, что полная волновая функция молекулы может быть выражена в виде произведения электронной и ядерной функций. Это предположение было предложено Максом Борном и Робертом Оппенгеймером и носит название аппроксимации Борна-Оппенгеймера: [math]\Psi_{total}(r,R) = \Psi_e(r,R) \cdot \Psi_N(R).[/math] Таким образом уравнение ([eq:Shrodinger]) перепишется в виде: [math]\label{eq:electron_motion} \left[ T_e + V_{ee}(r) + V_{eN}(r,R) \right] \Psi_e = \varepsilon(R) \Psi,[/math] [math]\label{eq:nucleus_motion} \left[T_N + V_{NN}(R) + \varepsilon(R) \right] \Psi_N(R) = E_N \Psi_N.[/math] Уравнение ([eq:electron_motion]) описывает движение электронов, считая ядра закрепленными. Функция [math]\varepsilon(R)[/math] зависит параметрически от положения ядер. В классической квантовой теории нахождение функции [math]\varepsilon(R)[/math] осуществляется точно, однако возможно заменить ее эмпирическим потенциалом. Тогда найденная функция подставляется в уравнение ([eq:nucleus_motion]). Отметим, что тогда уравнение ([eq:nucleus_motion]) не содержит электронных степеней свободы. В таком случае возможно заменить уравнение Шредингера на второй закон динамики Ньютона: [math]M \frac{d^2 R}{dt^2} = - \frac{d}{dR} \left( V_{NN}(R) + \varepsilon(R) \right).[/math] Таким образом возможно использование эмпирических данных, полученных из квантовой механики, и экспериментальных данных для описания межатомных взаимодействий на основании классических законов механики. При этом параметры полученного эмпирического описания подбираются таким образом, чтобы описывать необходимые свойства вещества. модели, описывающей переходные процессы на межатомном уровне, при этом позволяющей проводить моделирование больших атомарных систем, является особенно актуальной проблемой в связи с исследованиями в области нанотехнологий и механики дискретных систем.

Описание модели

Физическая модель

Предлагается представление атома как набора материальных точек. Используется модификация модели, предложенной Р.В. Власовым, Е.А. Ивановой, A.М. Кривцовым . Атом представляется в виде набора материальных точек. Одна материальная точка представляет центр масс ядра атома, остальные – центры масс электронных плотностей облаков. Количество точек, представляющих электронные облака равно максимальной степени окисления элемента. Конкретные силы взаимодействия и их параметры выбираются таким образом, чтобы материальные точки представляющие электронные облака находились на одинаковом расстоянии от ядра атома и располагались равномерно в пространстве вокруг ядра. Материальные точки представляющие центры масс ядер разных атомоы отталкиваются так как заряжены положительно. Материальные точки, представляющие центры электронных плотностей электронных облаков разных атомов, притягиваются, образуя химическую связь, при этом связь обладает свойством насыщения, то есть при сближении двух материальных точек они перестают взаимодействовать с остальными.

Взаимодействие материальных точек представляющих один атом

Для описания взаимодействия между материальной точкой, представляющей электронное облако предлагается использовать линейную упругую силу: [math]\mathbf{F}(\mathbf{r_i}) = C\mathbf{r_i},[/math] где [math]\mathbf{r_i}[/math] — радиус вектор, соединяющий материальную точку, представляющую ядро атома и материальную точку, представляющую центра электронной плотности облака и индексом [math]i[/math], [math]C[/math] — жесткость линейного взаимодействия. описания взаимодействия между материальными точками представляющими центры масс электронных облаков используется сила Кулона: [math]\mathbf{f}_{ij}(\mathbf{r}_{ij})=k_e\frac{q_i q_j}{r_{ij}^3}\mathbf{r}_{ij},[/math] где [math]\textbf{r}_{ij}=\textbf{r}_i-\textbf{r}_j[/math], [math]k_e[/math] — элекростатическая константа [math]q_i[/math], [math]q_j[/math] — заряды [math]i[/math]-го и [math]j[/math]-го облака. Такой выбор сил для описания взаимодействия материальных точек, описывающих атом, соответствует теории отталкивания электронных пар (Valence shell electron pair repulsion (VSEPR)), разработанной Р. Гиллеспи и Р. Найхолмом в 1957 г.

Межатомное взаимодействие

облаков разных атомов должно удовлетворять условию насыщения. Т.е. когда расстояние между материальными точками, представляющими центры электронных плотностей электронных облаков разных атомов, становится мало их взаимдействие с материальными точками, представляющими центры электронных плотностей электронных облаков остальных атомов, становится пренебрежимо мало. Для этого используется многочастичное взаимодействие предложенное А.М. Кривцовым, Е.А. Ивановой, Р.В.Власовым : [math]f_{ij}(r_{ij},s_i,s_j)=-s_i s_j P \left( \frac{a}{r_{ij}} \right)^q,[/math] где [math]f_{ij}[/math] — сила действующая на частицу [math]i[/math] со стороны частицы [math]j[/math], [math]r_{ij}[/math] — расстояние между частицами [math]i[/math] и [math]j[/math]. [math]a[/math], [math]P[/math], [math]q[/math] — параметры взаимоедйствия. Множитель [math]s_i[/math] определяется следующим соотношением: [math]s_i = \frac{1}{1 +\sum_{k \in N} {\left(\frac{a}{r_{ik}}\right)}^{0.5(1+q)}},[/math] где [math]r_{ij}[/math] — расстояние между частицами [math]i[/math] и [math]k[/math], [math]N[/math] — множество облаков не принадлежащих данному атому.

Насыщение связи

Приведенный вид взаимодействия между материальными точками, представляющими электронные плотности электронных облаков, обеспечивает насыщение связи. Рассмотрим материальные точки, представляющие центры электронных плотностей электронных облаков с индексами [math]i[/math] и [math]k[/math], которые находятся на небольшом расстоянии друг от друга. Для частицы с индексом [math]i[/math] имеем: [math]\frac{a}{r_{ij}} \stackrel{r_{ij} \to 0}{\longrightarrow} \infty [/math], [math]s_i = \frac{1}{1 +\sum_{k \in N} {\left(\frac{a}{r_{ij}}\right)}^{0.5(1+q)} + \ldots} \stackrel{r_{ij} \to 0}{\longrightarrow} 0.[/math] Таким образом взаимодействие облака с индексом [math]i[/math] с любым другим облаком, принадлежащим другому атому, для определенности обозначим его индексом [math]k[/math], [math]k \in N[/math], где [math]N[/math] — множество облаков, не принадлежащих данному атому, становится пренебрежимо мало: [math]f_{ik}(r_{ik},s_i,s_k)=-s_i s_k P \left( \frac{a}{r_{ik}} \right)^q \stackrel{s_i \to 0}{\longrightarrow} 0.[/math] Рассмотрим предложенное взаимодействие более подробно. Рассмотрим два облака, принадлежащие разным атомам, расстояние между которыми [math]r[/math]. Будем считать, что влияние остальных облаков пренебрежимо мало. Тогда выражение для силы записывается в следующем виде: [math]\label{eq:cloud_force} f (r) = - \left( \frac{1}{ 1+ \left( \frac{a}{r} \right) ^{ 0.5(1+q) } } \right) ^2 P \left( \frac{a}{r} \right) ^q.[/math] Преобразовав выражение ([eq:cloud_force]) получаем: [math]f = - P\left( \frac{1}{ \left( \frac{r}{a} \right)^\frac{q}{2} + \left( \frac{a}{r} \right) ^\frac{1}{2} } \right)^2 = - P\left( \frac{1}{ \left( \frac{r}{a} \right)^\frac{q+1}{2} + 1 } \right)^2 \frac{r}{a}.[/math] Положим [math]\frac{r}{a} = \rho[/math]: [math]\label{eq:cloud_non_dimensional} f (\rho) = - P\frac{ \rho }{ \left( 1 + \rho ^ \frac{q+1}{2} \right)^2}.[/math] Энергия взаимодействия получается интегрированием выражения ([eq:cloud_non_dimensional]) 0 до [math]\infty[/math] по [math]\rho[/math]. Положив [math]\frac{q+1}{2} = \alpha [/math] получаем: [math]\label{eq:electron_interaction_energy} D_{ee} = -\int\limits_{0}^{\infty} f(\rho)d\rho = -\frac{1}{2}aP\int\limits_{0}^{\infty} \frac{ \rho d\rho }{\left( 1+\rho^\alpha \right)^2} = - \frac {1}{2}aP \frac{\pi \left( \frac{2}{\alpha} - 1 \right) }{\alpha \sin\left( \frac{2 \pi}{\alpha} \right) }.[/math] [math]\begin{split} \Pi(\rho)& = \frac{1}{2}aP \int \frac{ \rho d\rho }{\left( 1+\rho^\alpha \right)^2} = \\ & = \frac{1}{4 \alpha}aP\rho^2 \left( \left( \alpha -2 \right) {_2F_1} \left(1, \frac{2}{\alpha}, \frac{ \alpha +2}{ \alpha} ,-\rho^\alpha \right) + \frac{2}{ \rho^\alpha + 1} \right) + C, \end{split}[/math] где [math]_2F_1[/math] — гипергеометрическая функция. Константа интегрирования находится из условия [math]\Pi(0) = 0[/math], [math]C = -D_{ee}[/math], где [math]D_{ee}[/math] — потенциальная энергия взаимодействия, найденная в уравненнии ([eq:electron_interaction_energy]). качественный вид зависимости силы и потенциальной энергии взаимодействия в безразмерном виде рис. [pic:cloud_interation].

Уравнения движения и численное интегрирование

Уравнения движения

Рассматривается система из [math]N[/math] частиц. В случае консервативной системы получаем следующие уравненя движения i-й частицы: [math]m_i \frac{ \partial \textbf r_i}{ \partial t} = \sum\limits_{k=1..N} \textbf F_{ik},[/math] где [math]m_i[/math] “— масса [math]i[/math]-й частицы, [math]\textbf r_i[/math] ”— радиус вектор от i-й частицы, [math]\textbf F_i[/math] "— сила действующая на частицу i со стороны частицы k. Эта система дифференциальных уравнений не может быть решена аналитически, однако может быть произведено численное интегрирование с шагом по времени [math]\Delta t[/math]. Сходимость результата, получаемого численным интегрированием, во многом зависит от правильного выбора шага [math]\Delta t[/math], чем меньше значение [math]\Delta t[/math] тем точнее получаемый результат. В то же время чем меньше шаг, тем больше длительность расчета выбранного промежутка времени моделирования системы. Грамотный выбор шага интегрирования решаюшим образом влияет на сходимость и должен быть произведен в соответствии с конкретной задачей. В процессе интегрирования на каждом шаге подсчитываются характеристики частиц такие как координата, скорость и суммарная действующая на частицу сила. В этом случае необходимо использовать быстрые и точные численные алгоритмы применимые к решению подобных систем дифференциальных уравнений.

Алгоритм Верле

Алгоритм Верле основан на сумме двух симметричных разложений в ряд Тейлора [math]r(t + \Delta t)[/math] и [math]r(t - \Delta t)[/math]: [math]r_i(t + \Delta t) = r_i(t) + \Delta t \dot{r_i} (t) + \frac{1}{2}( \Delta t)^2 \ddot{r_i}(t) + \ldots[/math]

[math]r_i(t - \Delta t) = r_i(t) - \Delta t \dot{r_i} (t) + \frac{1}{2}( \Delta t)^2 \ddot{r_i}(t) - \ldots[/math]

Просуммируем эти выражения. После суммирования исчезают слагаемые, содержащие нечетные степени [math]\Delta t[/math]. Таким образом скорости не входят в выражение для суммы. Перенося в правую часть [math]r_i(t - \Delta t)[/math] получаем выражение для определения координаты на следующем шаге интегрирования: [math]r_i(t + \Delta t) = 2r_i(t) - r_i(t - \Delta t) + ( \Delta t)^2 \ddot{r_i}(t) + \ldots[/math] [math]r_i(t)[/math] находится следующим образом: [math]\ddot{r_i} = \frac{F_i}{m},[/math] где [math]F_i[/math] — суммарная сила, действующая на частицу с индексом [math]i[/math] на текущем шаге интегрирования. Скорость может быть найдена вычитанием: [math]\label{eq:verle_vel} \dot{r_i}(t) = \frac{r_i(t + \Delta t) - r_i(t - \Delta t)}{2 \Delta t}.[/math] В силу симметрии алгоритма, алгоритм Верле является обратимым по времени. Использование алгоритма Верле гарантирует сохранение энергии для малых шагов интегрирования.

Алгоритм ’Leapfrog’

Алгоритм ’Leapfrog’ представляет собой модификацию алгоритма Верле, в котором скорость используется как промежуточный результат испольуемый для подсчета следующего шага. В отличие от метода Верле, где решается одно дифференциальное уравнение второго порядка, в методе Leapfrog решаются два уравнения первого порядка. Подсчет скоростей ведется на шаге, смещенном на [math]\frac{\Delta t}{2}[/math] относительно подсчета координат [math]r_i[/math]: [math]\begin{cases} r_i(t + \Delta t) = r_i(t + \Delta t) + \Delta \dot{r_i} (t+ \frac{ \Delta t}{2}) \\ \dot{r_i}(t + \frac{\Delta t}{2} ) = \dot{r_i}(t - \frac{\Delta t}{2} ) + \Delta t \ddot{r_i}(t) \end{cases}.[/math] При необходимости можно подсчитать скорость на текущем шаге, как среднее скоростей на двух соседних шагах: [math]\dot{r_i} = \frac{ \dot{r_i}(t + \frac{\Delta t}{2} ) + \dot{r_i}(t - \frac{\Delta t}{2} ) }{2}.[/math]

Качественные результаты

Постановка задачи

Были проведены численные эксперименты со следующими безразмерными параметрами [math]q = 4[/math], [math]K_{NN} = 0.1[/math], [math]K_{eN} = 1[/math], размерными параметрами [math]a = 1[/math], [math]P =1[/math]: [math]\begin{aligned} K_{eN} = \frac{aC}{P}, ~~~ K_{NN} = \frac{k_e q_i q_j}{Pa^2} ,\end{aligned}[/math] где [math]k_e[/math] — элекростатическая константа [math]q_i[/math], [math]q_j[/math] — заряд [math]i[/math] и [math]j[/math] частицы. В качестве шага интегрирования был выбран [math]\Delta t = 0.0001[/math]. В качестве начальных условий были заданы случайные скорости. Было проводено моделирование образования различных классов химических веществ.

Образование углеводородов

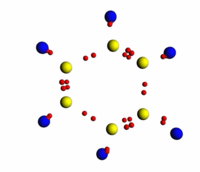
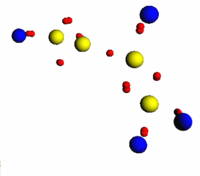
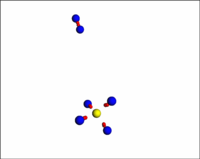
Была рассмотрена система, состоящая из 20 атомов углерода (С) и 60 атомов водорода (H). Наблюдалось образование молекул из атомарного газа. Результаты моделирования приведены на рис. [pic:vinylacet]

Наблюдается образование органических соединений, таких как метан [math]\mathrm{CH_4}[/math], этилен [math]\mathrm{C_2H_4}[/math] и более сложных углеводородов, таких как винилацетилен [math]\mathrm{C_4H_4}[/math]. Данный пример показывает возможность описания химических связей различной кратности (одинарная, двойная, тройная), а также возможность описания полиядерных молекул, то есть молекул, состоящих из атомов нескольких химических элементов.

Результаты

Количественное описание

Параметризация модели

того чтобы понять физический смысл параметров, содержашихся в модели, необходимо найти соотношения, связывающие их с величинами, полученными в реальном физическом эксперименте. Полученные соотношения позволят проводить моделирование реальных физических процессов и количественно описывать наблюдаемые явления. Для того чтобы получить выражение параметров модели через данные, полученные в эксперименте, рассматривается парное взаимодействие двух атомов углерода. Рассматривается взаимодействие материальных точек, представляющих центры масс ядра и материальных точек, представляющих центры электронных плотностей электронных облаков, лежащих на линии, соединяющей центры масс ядер. Влияние остальных частиц в рамках рассматриваемой задачи не учитывается. Изображение рассматриваемой системы приведено на рис. [pic:carbon].

Получим выражения для имеющихся в системе сил через безразмерные параметры. Линейная упругая сила взаимодействия между электронным облаком и ядром [math]F_{eN}[/math] и кулоновское отталкивание ядер [math]F_{NN}[/math] могут быть записаны в следующем виде: [math]F_{eN} = -Cr = -K_{eN}P \frac{r}{a},[/math]

[math]F _{NN} = k_e\frac{q_i q_j}{r^2}= K_{NN}P \left( \frac{a^2}{r^2} \right),[/math]

где [math]\label{eq:dimen_param} C = K_{eN}\frac{P}{a}, k_eq_iq_j = K_{NN} P a^2.[/math]

Переменные [math]K_{eN}[/math] и [math]K_{NN}[/math] являются безразмерными. Параметры [math]a[/math] и [math]P[/math] имеют размерность длинны [м] и силы [Н] соответственно. Физический смысл размерных заключается в масштабировании рассматриваемого взаимодействия. За единицу масштаба примем соответственно длину и прочность углерод-углеродного взаимодействия [math]r_0[/math] и [math]f^*[/math]. Так как, вообще говоря, параметры [math]a[/math] и [math]P[/math] могут не совпадать соответственно с длиной и прочностью связи, введем дополнительные безразмерные параметры [math]\varepsilon[/math] и [math]\eta[/math] — коэффициенты пропорциональности между длиной связи [math]r_0[/math] и [math]a[/math] и прочностью связи [math]f^*[/math] и [math]P[/math]: [math]\label{eq:scale_param} P = \varepsilon f^*,~~~ a = \eta r_0.[/math] Таким образом предложенное взаимодействие описывается следующим набором параметров:

• размерные [math]P[/math], [math]a[/math]
• безразмерные [math]K_{eN}[/math], [math]K_{NN}[/math], [math]q[/math], [math]\eta[/math], [math]\varepsilon[/math]

силы действующие в системе. Обозначим за [math] F_{ee}[/math] силу взаимодействия двух электронных облаков. Геометрический смысл переменных [math]r[/math] и [math]x[/math] приведен на рис. [pic:carbon]

[math]\label{eq:el_el_force} F_{ee} = \frac{P}{ \left(1 + \left( \frac{a}{2x} \right) ^ {\frac{1+q}{2}} \right)^2} \left( \frac{a}{2x} \right)^q,[/math] [math]\label{eq:el_nuc_force} F_{eN}=C\left(r-x\right).[/math] Так как система находится в равновесии [math]F_{ee} = F_{eN}[/math]. Приравнивая выражения ([eq:el_el_force]) и ([eq:el_nuc_force]) получаем:

[math]r = x + \frac{P}{C} \frac{ \left( \frac{a}{2x}\right)^q}{\left(1+\left(\frac{a}{2x}\right) ^ {\frac{1+q}{2}}\right)^2}.[/math] Выражение для суммарной силы действующей на ядро примет следующий вид: [math]f(x)= \frac{P}{ \left(1 + \left( \frac{a}{2x} \right) ^ {\frac{1+q}{2}} \right)^2} \left( \frac{a}{2x} \right)^q + k_e \frac{4Q^2}{\left( x + \frac{P}{C} \frac{ \left( \frac{a}{2x}\right)^q}{\left(1+\left(\frac{a}{2x}\right) ^ {\frac{1+q}{2}}\right)^2} \right)^2},[/math] где [math]Q[/math] - заряд ядра. Таким образом зависимость силы, действующей на атомы, в зависимости от расстояния между ними задется неявно следующим образом:

[math]\begin{cases} f(x)= -\frac{P}{ \left(1 + \left( \frac{a}{2x} \right) ^ {\frac{1+q}{2}} \right)^2} \left( \frac{a}{2x} \right)^q + k_e \frac{4Q^2}{\left( x + \frac{P}{C} \frac{ \left( \frac{a}{2x}\right)^q}{\left(1+\left(\frac{a}{2x}\right) ^ {\frac{1+q}{2}}\right)^2} \right)^2}, \\ r(x) = x + \frac{P}{C} \frac{ \left( \frac{a}{2x}\right)^q}{\left(1+\left(\frac{a}{2x}\right) ^ {\frac{1+q}{2}}\right)^2}. \end{cases}[/math]

Обозначим [math]\xi = \frac{2x}{a}[/math]. Используя соотношения ([eq:dimen_param]) и ([eq:scale_param]) перепишем полученные выражения в безразмерных величинах: [math]\label{dimensionless_force} \begin{cases} \frac{f(\xi)}{f^*} =\varepsilon \left( -\frac{1}{ \left(1 + \xi\ ^ {-\frac{1+q}{2}} \right)^2} \xi^{-q} + \frac{4K_{NN}}{\left( \frac{1}{2}\xi + \frac{1}{K_{eN}} \frac{ \xi^{-q}}{\left(1+\xi ^ {-\frac{1+q}{2}}\right)^2} \right)^2} \right), \\ \frac{r(\xi)}{r_0} =\eta \left( \frac{1}{2}\xi + \frac{1}{K_{eN}} \frac{ \xi^{-q}}{\left(1+\xi ^ {-\frac{1+q}{2}}\right)^2} \right). \end{cases}[/math] Обозначим функции, стоящие в правых частях уравнений из системы ([dimensionless_force]), за [math]\zeta(\varepsilon, \xi, q, K_{eN}, K_{NN} )[/math], [math]\Psi(\eta, \xi, q, K_{eN}, K_{NN} )[/math].

Тогда система примет вид:

[math]\begin{cases} \frac{f(\xi)}{f^*} =\zeta(\varepsilon, q, K_{eN}, K_{NN}; \xi ), \\ \frac{r(\xi)}{r_0} =\Psi(\eta, q, K_{eN}; \xi ). \end{cases}[/math] Рассмотрим параметры реальной физической системы. Обозначим [math]\varepsilon^*[/math] “— безразмерный коэффициент определяемый соотношением: [math]\begin{aligned} r_* = (1 + \varepsilon_*)r_0, ~~~ \frac{\xi^*}{\xi_0}= \frac{r^*}{r_0},\end{aligned}[/math] [math]\varepsilon^* = \frac{\xi^*}{\xi_0} - 1,[/math] где [math]\xi_0 = \frac{2x_0}{a}[/math], [math]\xi^* = \frac{2x^*}{a}[/math],

где [math]x_0[/math], [math]x^*[/math] ”— расстояние равновесия и отрыва соответственно для координаты точки, представлящей центр масс электронного облака. записать набор уравнений, описывающий различные физические состояния системы:

• равенство нулю силы в положении равновесия:

[math]\label{eq:equilibrium} \begin{cases} \zeta(\varepsilon, q, K_{eN}, K_{NN}; \xi_0 ) = 0, \\ \Psi(\eta, q, K_{eN}; \xi_0) = 1 . \end{cases}[/math]

• жесткость в положении равновесия:

[math]\label{eq:stiffness} \begin{cases} \zeta'_\xi(\varepsilon, q, K_{eN}, K_{NN}; \xi_0 ) = -\frac{Cr_0}{f^*}, \\ \Psi(\eta, q, K_{eN}; \xi_0 ) = 1. \end{cases}[/math]

• максимум силы в момент отрыва:

[math]\label{eq:max_force} \begin{cases} \zeta'_\xi(\varepsilon, q, K_{eN}, K_{NN}; \xi^*) = 0, \\ \Psi(\eta, q, K_{eN};\xi^*) = 1+ \varepsilon*. \end{cases}[/math]

• равенство силы прочности связи в момент отрыва:

[math]\label{eq:critical_len} \begin{cases} \zeta(\varepsilon, q, K_{eN}, K_{NN} ;\xi^*) = -1, \\ \Psi(\eta, q, K_{eN};\xi^* ) = 1+ \varepsilon*. \end{cases}[/math]

• энергия связи:

[math]\label{eq:energy} \begin{cases} \int\limits_{\xi_0}^\infty \zeta ( \varepsilon, q, K_{eN}, K_{NN}; \xi )d\xi = -\frac{D}{r_0 f^*}, \\ \Psi(\eta, q, K_{eN} ;\xi_0) = 1. \end{cases}[/math]

Приведем экспериментальные данные для углерод-углеродного взаимодействия, взятые из работы :

[math]\label{experiment} \begin{aligned} &D = 0.7899 \: \text{нН} \cdot \text{нМ}, \\ &r_0=0.1430 \: \text{нМ}, \\ &r^* = 0.1859 \: \text{нМ}, \\ &C = 800 \: \text{Н/м}, \\ &f^* = \frac{C(r^*-r_0)}{k_*}=\frac{800 \cdot (0,1859 - 0,01430)}{3,1000}=11,0710 \: \text{нН}, \end{aligned}[/math] где [math]D[/math] — энергия связи, [math]r_0[/math] — Равновесное расстояние, [math]r^*[/math] — критическая длина связи, [math]f^*[/math] — прочность связи, [math]C[/math] —жесткость связи, [math]k^*[/math] — коэффициент нелинейности. Таким образом такое взаимодействие полностью описывается тремя безразмерными константами, которые можно найти из экспериментальных данных:

[math]\label{eq:experiment_constant} \begin{aligned} &\alpha = \varepsilon^* +1 = 1.30, \\ &\beta= \frac{Cr_0}{f^*} = 10.33,\\ &\gamma= \frac{D}{r_0 f^*} = 0.28. \\ \end{aligned}[/math]

Сравнение предложенной модели с простейшими потенциалами

Рассмотрим применение существующих потенциалов к описанию данной системы. Парные потенциалы взаимодействия и соотношения для их параметров подробно описаны в работе .

Потенциал Леннарда-Джонса

Для потенциала Леннарда-Джонса имеем следующие соотношения:

[math]\begin{aligned} &f^* = 2.7 \frac{D}{r_0}, ~~~ &C = 72 \frac{D}{r_0}. \end{aligned}[/math]

Найдем константы [math]\alpha[/math], [math]\beta[/math] и [math]\gamma[/math] для потенциала Леннарда-Джноса и сравним их с углеродным взаимодействием: [math]\begin{aligned} &\alpha_{LJ} = 1.1, \\ &\beta_{LJ} = \frac{Cr_0}{f^*} = \frac{72 \frac{D}{r_0^2}r_0}{2.7\frac{D}{r_0}} = 26.67, \\ &\gamma_{LJ} = \frac{D}{r_0 f^*} = 2.7. \\ \end{aligned}[/math]

Видно, что безразмерный коэффициент [math]\beta[/math], подсчитанный для потенциала Леннарда-Джонса, отличается от подобного для углеродного взаимодействия на 158 %. Коэффициент [math]\gamma[/math] отличается на 850 %. Это говорит о том, что потенциал Леннарда-Джонса не может точно описывать жесткостных и энергетических характеристик углерод-углеродного взаимодействия.

Потенциал Морзе

Для потенциала Морзе имеем:

[math]\begin{aligned} &\alpha_{morse} = \frac{1}{\alpha a}\ln 2 +1 = \frac{\ln 2}{k_\nu} +1, \\ &\beta_{morse} = \frac{2 \alpha^2 D \frac{ k_\nu}{\alpha}}{ \frac{\alpha D}{2}} = 4, \\ &\gamma_{morse} = \frac{D}{\frac{\alpha D k_\nu}{2 \alpha}} = 2.\\ \end{aligned}[/math]

Коэффициент [math]\alpha_M[/math] можно сделать равным [math]\alpha_C[/math] выбором константы [math]k_\nu[/math]. [math]\beta[/math] отличается на 61 %. [math]\gamma[/math] отличается на 300 %. С помощью потенциала Морзе углерод-углеродное взаимодействие можно описать более точно чем с помощью потенциала Леннарда-Джонса, параметр [math]\alpha[/math] можно подобрать точно, отличие [math]\beta[/math] и [math]\gamma[/math] меньше, однако все еще слишком велико, чтобы можно было говорить о точном описании угредоного взаимодействия с помощью этого потенциала.

Потенциал Ми

Потенциал Ми является обобщением потенциала Леннарда-Джонса. Рассмотрим можно ли удовлетворить константам [math]\alpha[/math], [math]\beta[/math] и [math]\gamma[/math] с помощью параметров потенциала:

[math]\begin{aligned} &\alpha_{Mi} = \sqrt[n-m] {\frac{n+1}{m+1} }, \\ &\beta_{Mi} = \sqrt[m-n]{ \frac{(m+1)^{(m+1)}}{(n+1)^{(n+1)}}}, \\ &\gamma_{Mi} = \frac{1}{mn} \sqrt[m-n]{ \frac{(m+1)^{(m+1)}}{(n+1)^{(n+1)}}}. \end{aligned}[/math]

Имеем систему из трех уравнений и двух неизвестных [math]m[/math] и [math]n[/math]. Решая систему, можно будет точно удовлетворить только двум уравнениям.

Предложенная модель

Используя экспериментальные данные ([experiment]) и соотношения ([eq:equilibrium]), ([eq:stiffness]), ([eq:max_force]), ([eq:critical_len]) и ([eq:energy]) можем записать систему. систему уравнений, содержащую 6 безразмерных неизвестных [math]K_{eN}[/math], [math]K_{NN}[/math], [math]\xi_0[/math], [math]\xi^*[/math], [math]\eta[/math],[math]\epsilon[/math] связывающую параметры модели:

[math]\label{eq:dimenless_system} \begin{cases} \Psi(\eta, q, K_{eN}; \xi_0) = 1, \\ \Psi(\eta, q, K_{eN};\xi^*) = \frac{r^*}{r_0},\\ \zeta(\varepsilon, q, K_{eN}, K_{NN}; \xi_0 ) = 0, \\ \zeta'_\xi(\varepsilon, q, K_{en}, K_{NN}; \xi_0 ) = -\frac{Cr_0}{f^*}, \\ \zeta(\varepsilon, q, K_{eN}, K_{NN} ;\xi^*) = -1, \\ \zeta'_\xi(\varepsilon, q, K_{eN}, K_{NN}; \xi^*) = 0. \\ \end{cases}[/math]

Из соотношения ([dimensionless_force]) видно, что функции [math]\Psi[/math] и [math]\zeta[/math] зависят от [math]\eta[/math] и [math]\varepsilon[/math] линейно, можем обозначить: [math]\begin{aligned} \label{eq:zeta_psi} &\Psi(\eta, q, K_{eN}; \xi) = \eta \widetilde{\Psi}(q, K_{eN}; \xi),\\ &\zeta(\varepsilon, q, K_{eN}, K_{NN}; \xi_0 ) =\varepsilon \widetilde{\zeta} (q, K_{eN}, K_{NN}; \xi ) \end{aligned}[/math]

Тогда возможно исключить из системы ([eq:dimenless_system]) переменные [math]\eta[/math] и [math]\varepsilon[/math]. Тогда система имеет 4 неизвестных переменных и перепишется в следующем виде:

[math]\begin{cases} \frac{ \widetilde{\Psi}( q, K_{eN} ;\xi^*) }{ \widetilde{\Psi}( q, K_{eN} ;\xi_0)} = \frac{r^*}{r_0}, \\ \frac{ \widetilde{\zeta}'_\xi(q, K_{eN}, K_{NN}; \xi_0 )}{\widetilde{\zeta} (q, K_{eN}, K_{NN} ;\xi^*)} = \frac{Cr_0}{f^*}, \\ \widetilde{\zeta}'_\xi(q, K_{eN}, K_{NN}; \xi^*) = 0, \\ \widetilde{\zeta}(q, K_{eN}, K_{NN}; \xi_0 ) = 0. \\ \end{cases}[/math] Будем решать следующую систему, рассматривая показатель степени q как параметр и приняв q = 5. Подставляя данные из соотношений ([experiment]), получим: [math]\begin{cases} \frac{ \widetilde{\Psi}( q, K_{eN};\xi^*) }{ \widetilde{\Psi}( q, K_{eN};\xi_0)} - 1.30 = 0, \\ \frac{ \widetilde{\zeta}'_\xi(q, K_{eN}, K_{NN}; \xi_0 )}{\widetilde{\zeta} (q, K_{eN}, K_{NN} ;\xi^*)} - 10.33 = 0, \\ \widetilde{\zeta}'_\xi(q, K_{eN}, K_{NN}; \xi^*) = 0, \\ \widetilde{\zeta}(q, K_{eN}, K_{NN}; \xi_0 ) = 0. \\ \end{cases}[/math]

Решение системы выполняется комбинированным методом Монте-Карло  и методом Левенберга — Марквардта . На рис. [pic:montecarlo] приведена визуализация выбора начального приближения. Начальное приближение выбирается случайным образом, далее выполняется итерационный метод. При этом необходимо выполнение условия [math]\xi^* \gt  \xi_0[/math].

Так как система нелинейна, она может иметь вообще говоря бесконечное количество решений, однако в результате расчета в выбранных пределах задания начального приближения имеем единственное решение:

[math]\begin{cases} \xi_0 = 0.4689,\\ \xi^* = 0.7105,\\ K_{eN} = 2.3017,\\ K_{NN} = 0.0622.\\ \end{cases}[/math] Переменные [math]\varepsilon[/math] и [math]\eta[/math] находятся из соотношений ([eq:zeta_psi]) и ([eq:dimenless_system]): [math]\begin{aligned} \eta = \frac{1}{ \widetilde{\Psi} ( q, K_{eN}; \xi_0)}, \\ \varepsilon = \frac{1} {\widetilde{\zeta}( q, K_{eN}, K_{NN} ;\xi^*)}. \end{aligned}[/math]

Приведем зависимость суммарной силы, действующей на ядро, от расстояния между ядрами в безразмерном виде [math]\zeta(\xi)[/math] рис. [pic:f_dependance]

Рассмотрим выполнение соотношений ([eq:experiment_constant]) для полученных значений параметров. Выполнение соотношений для констант [math]\alpha[/math] и [math]\beta[/math] следует из выполнения системы ([eq:dimenless_system]). Значение параметра [math]\gamma[/math] находится из соотношения: [math]\gamma = \int\limits_{\xi_0}^\infty \zeta ( \varepsilon, q, K_{eN}, K_{NN}; \xi ) \Psi'_\xi ( \varepsilon, q, K_{eN}; \xi )d\xi = 4.99.[/math] Так как нас интересует энергия связи на отрыв, интегрирование проводится только по тому отрезку, где функция [math]\zeta[/math] принимает отрицательное значение. Отличие полученного значения [math]\gamma[/math] от значения, полученного из экспериментальных данных ([eq:experiment_constant]), составляет 10%, что говорит о применимости предложенной модели к описанию энергетических свойств взаимодействия. Приведем полный список параметров в таблице [tab:parameters].

Полный список параметров модели.

[math]\xi_0[/math]	[math]\xi^*[/math]	[math]K_{eN}[/math]	[math]K_{NN} [/math]	[math]\varepsilon[/math]	[math]\eta[/math]	[math]q[/math]
0.4689	0.7105	2.3017	0.0622	6.3760	2.4880	5.0000

Результаты моделирования

Проведено моделирование образования углеводородов с полученными значениями параметров. Визуализация результатов приведена на рис. [pic:molecules]. Результаты моделирования качественно совпадают с результатами описанными в главе [ch:qual], однако теперь возможно количественное описание системы, исследование макроскопических характеристик вещесва, таких как температура, давление и т.д.

Заключение

В данной работе были исследованы эффекты, связанные с насыщением межатомной связи в сложных молекулярных структурах. Была разработана модель межатомных взаимодействий, основанная на законах классической механики, описывающая насыщение межатомной связи. Было проведено молекулярное моделирование образования молекулярных структур различных химических элементов. Было показано что предложенная модель качественно описывает известную геометрию молекул для широкого ряда химических соединений. Получены выражения позволяющие связывать параметры предложенной модели и параметры межатомного взаимодействия известные из теории и эксперимента. Проведена параметризация модели для углерод-углеродного взаимодействия. Проведено сравнение, предложенной модели с существующими потенциалами взаимодействия. Предложенная модель может быть использована для подбора оптимальных параметров эксперимента, исследования влияния переходных процессов на межатомном уровне на макроскопические характеристики вещества и дальнейших теоретических исследований.

Автор хотел бы поблагодарить Виталия Андреевича Кузькина за полезные обсуждения

Ссылки

http://www.sciteclibrary.ru/rus/catalog/pages/11938.html