Определение эффективных упругих характеристик в материале с трещинами

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск

МАГИСТЕРСКАЯ РАБОТА
Автор работы: Р. Л. Лапин
Руководитель: доцент кафедры ТМ В. А. Кузькин

Введение

Задачи связанные с учетом трещин в материале исследуются в различных научных областях:

  • Механика твердого тела
  • Геология
  • Механика материалов
  • Нефтедобыча и газодобыча

Включения (трещины, поры) могут значительно влиять на эффективные модули материала – уменьшать компоненты тензора жесткости в несколько раз. Определение эффективных характеристик является важной задачей. Первым приближением является приближение невзаимодействия - каждая трещина считается изолированной, и не чувствует влияния соседних трещин. Результаты полученные с помощью данного метода могут значительно отличаться от полученных другими методами. Однако, в приближении невзаимодействия доказано - материал с трещинами при любой конфигурации трещин является ортотропным. Важным вопросом является вопрос - будет ли он ортотропным при учете взаимодействия.

Постановка задачи

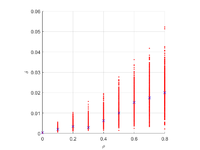
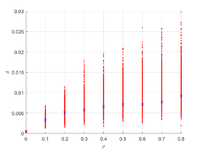
Исследуется материал со случайно расположенными трещинами в плоско-деформированной постановке. Характеристикой трещин является плотность [math]\rho = \frac{Nl^2}{4A} [/math], где [math]N [/math] - число трещин, [math]l[/math] - длина трещины, [math] A [/math] - площадь рассматриваемой области. Цель данной работы

  • Реализовать метода разрывных смещений на языке С++ для решения задач напряженно-деформированного состояния материала с различными конфигурациями при различных нагрузках.
  • Провести серию расчетов для различных постановок, с целью определения отклонения тензора податливости от ортотропного
    • Семейство параллельных трещин
    • Два семейства параллельных трещин при различных наклонах
    • Три семейства параллельных трещин
  • Определить углы ортотропии для постановок в которых отсутствует геометрическая ортотропия
  • Проанализировать полученные результаты.

Для каждой постановки рассматривается диапазон плотностей [math]\rho = [0.01;0.8][/math]. Для каждой плотности проводится операция усреднения - проводится 450-650 расчетов с различными конфигурациями.

Создание начальных конфигураций

Пример конфигурации трещин
Пример плохой конфигурации трещин с раскрытием трещин
Пример хорошей конфигурации

В ходе работы над задачей возникла проблема создания начальных конфигураций. При близком расположении трещин численный метод (метод разрывных смещений) неустойчив. В виду этого было определено минимальное расстояние достаточное для устойчивости - 0,1 длины трещины. Использование данного ограничения значительно улучшает результаты.

Оценка ортотропности

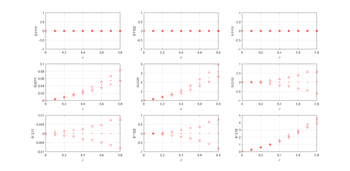
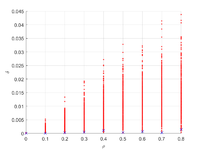
Отклонения для семейства параллельных трещин
Отклонения для семейства параллельных трещин

Вычисленный тензор податливости может отличаться от ортотропности, для оценки используется оценка [math]\delta = \sqrt{\frac{(S_{ijkl}-S_{ijkl}^{ort})(S_{ijkl}-S_{ijkl}^{ort})}{S_{prqs}S_{prqs}}}[/math]

Результаты отклонения тензора податливости дял семейства параллельных трещин не превышает 3%.


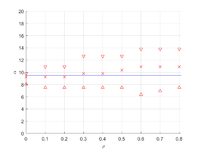
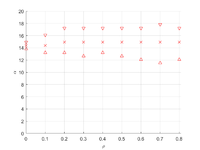
Определение углов ортотропии

Углы ортотропии могут отличаться от начальных осей. Для определения углов ортотропии предполагается минимум отклонения тензора податливости от ортотропного. Для поворота тензора подаливости используется тензор поворота, в матричном виде он имеет вид

[math]F = \begin{pmatrix} \cos \alpha^2 & \sin \alpha^2 & \sin 2\alpha \\ \sin \alpha^2 & \cos \alpha^2 & -\sin 2\alpha \\ -\frac{\sin \alpha}{2} & -\frac{\sin \alpha}{2} & \cos 2\alpha \end{pmatrix}[/math]

Для постановок двух и трех семейств трещин определены углы поворота к осям ортотропии

  • Для двух семейств:
    • Для наклоненных под углом [math]30^0[/math] - [math]9.5^0[/math]
    • Для наклоненных под углом [math]15^0[/math] - [math]5^0[/math]
    • Для наклоненных под углом [math]40^0[/math] - [math]18^0[/math]
  • Для трех семейств - [math]15^0[/math]
Углы к осям ортотропии для двух семейств трещин, наклоненных под углом 30 градусов
Углы к осям ортотропии для трех семейств трещин

Отклонение тензора податливости для всех постановок не превышает 5%.

Отклонение от ортотропного тензора для двух семейств трещин, наклоненных под углом 30 градусов
Отклонение от ортотропного тензора для трех семейств трещин


Выводы

В ходе работы были решены сразу несколько задач:

В работе над данной задаче были получены следующие результаты:

  • Реализован метод разрывных смещений на языке С++ в виде вычислительного модуля для определения эффективных свойств материала с трещинами, позволяющий решать задачи в различных постановках
  • Проведено тестирование метода для задачи об одной трещине под растягивающей внешней нагрузкой. Отклонение полученных результатов от аналитического решения для среднего раскрытия не превышает 3%.
  • Решена задача создания начальных конфигураций. Определено минимальное расстояние между трещинами, позволяющее повысить устойчивость численного метода. Данное расстояние соответствует 0.1 длины трещины.
  • Проведено сравнение численных значений компонент тензора жесткости для задачи о параллельных трещинах с известными решениями [1]. Получено хорошее качественное совпадение.
  • Для задачи двух семейств трещин, наклоненных под углом 300, определены углы поворота к осям ортотропии. Полученные результаты хорошо согласуются с известным аналитическим решением [3].
  • Определены углы поворота к осям ортотропии для постановок, в которых отсутствует геометрическая ортотропия. В частности, для задачи двух семейств трещин, наклоненных под углом [math]30^0[/math] – угол поворота [math]9^0[/math], наклоненных [math]15^0[/math] – [math]5^0[/math], наклоненных [math]40^0[/math] – [math]18^0[/math]. Для трех семейств трещин угол поворота – [math]15^0[/math].
  • Рассмотрены несколько постановок с различными семействами трещин (5 различных постановок) при различных плотностях. Для каждой плотности проведено 450 расчетов для реализации операции усреднения.
  • Исследовано влияние взаимодействия трещин на орторопные свойства материала с трещинами при различных постановках. Даже в материале, в котором отсутствует геометрическая ортотропия, наблюдается незначительное влияние взаимодействия –5%.

Материалы работы

Материал, посвященный работе.

Литература

1) VI Kushch, I Sevostianov, L Mishnaevsky, «Effect of crack orientation statistics on effective stiffness of mircocracked solid,» International Journal of Solids and Structures, т. vol.46, pp. 1574-1588, 2009.

2) Bernarn Budiamsky,Richard J. O'Connell, «Elastic moduli of a cracked solid,» International journal of Solids and structures, № 12, pp. 81-97, 1976.

3)M.Kachanov, «Elastic solids with many cracks and related problems,» ADVANCES IN APPLIED MECHANIC, т. vol.30, pp. 260-438, 1993.

4)Vladimir Grechka,Mark Kachanov, «Effective elasticity of rocks with closely spaced and intersecting cracks,» GEOPHYSICS, т. 71, № 3, pp. D85-D91, 2006.

5)Erik H. Saenger,Oliver S. Kruger and Serge A. Shapiro, «Effective elastic properties of randomly fractured soils: 3D numerical experiments,» Geophysical Prospecting, № 52, pp. 183-195, 2004.

6) Y.J. Liu, X.L. Chen, «Evaluations of the effective material properties of carbon nanotube-based composites using a nanoscale representative volume element,» Mechanics of Materials, № 35, pp. 69-81, 2003.

7) Y. BENVENISTE, «A new approach to the application of Mori-Tanaka's theory in composite materials,» Mechanics of Materials, № 6, pp. 147-157, 1987.

8) И. Баюк, «Основные принципы математического моделирования макроскопических физических свойств коллекторов углеводородов,» Seismic Technology , № 10, pp. 5-18, 2011.

9) И. Баюк, «Междисциплинарный подход к определению эффективных физических свойств коллекторов,» в Galperin Readings 2011 , Galperin , 2011.

10) Igor Sevostianov, Mark Kachanov, «On approximate symmetries of the elastic properties and elliptic orthotropy,» International Journal of Engineering Science, № 46, pp. 211-223, 2008.

11) M.Kachanov, «Effective elastic properties of cracked solids: critical review of some basic concepts,» Appl Mech Rev, № vol. 45, pp. 304-305, 1992.

12) Crouch S.L., Starfield A.M, «Boundary Element Methods in Solid Mechanics: with Applications in Rock Mechanics and Geological Engineering,» George Allen and Union, p. 322, 1983.

13) K. J. Willam, «Advanced Mechanics of Materials,» CVEN 5161, 2003.

Источник — «http://tm.spbstu.ru/?title=Определение_эффективных_упругих_характеристик_в_материале_с_трещинами&oldid=47421»