Исследование реологических свойств суспензий на основе моделирования методом динамики частиц

БАКАЛАВРСКАЯ РАБОТА
Автор работы: Поцелуев Павел
Научный руководитель: В. А. Кузькин

Введение

Суспензиями называются грубодисперсные системы с твёрдой дисперсной фазой (размер твердых частиц более [math]10^{-5} м[/math]) и жидкой дисперсионной средой. Такие смеси повсеместно встречаются как в промышленном производстве, так и в природных процессах. Именно поэтому исследованиям реологии суспензий уделяется много внимания: с начала XX века по данной тематике опубликованы сотни научных статей. Одним из примеров суспензии является смесь проппант-жидкость. Проппант (расклинивающий агент) - гранулообразный материал, который используется в нефтедобывающей промышленности для повышения эффективности отдачи скважин с применением технологии гидроразрыва пласта (ГРП). Служит для закрепления (предупреждения смыкания под действием горного давления) трещин, создаваемых в ходе ГРП. Представляет собой гранулы сходного размера, с типичным диаметром от 0,5 до 1,2 мм. В данной работе исследуется реологию смеси проппант-жидкость, хотя результаты применимы и для других суспензий.

Моделирование методом динамики частиц

Метод динамики частиц основан на моделировании среды совокупностью взаимодействующих частиц, для которых записываются классические уравнения динамики. Взаимодействие частиц описывается посредством потенциалов взаимодействия. В данной работе использовался потенциал Леннард-Джонса.

Для решения поставленной задачи мы численно интегрируем уравнения движения, предварительно задав начальные условия. После перехода течения в установившийся режим мы определяем характеристики течения, зная которые можем рассчитать эффективную вязкость смеси.

Определение эффективной вязкости смеси

Аналитические формулы, полученные в приближении невзаимодействия (предположение об отсутствии взаимного влияния полей возмущений, возникающих при обтекании частиц проппанта)
[math]μ(с)/(μ(0))=Ac+1 [/math] формула Эйнштейна
[math]μ(с)/(μ(0))=1/(1-Ac) [/math] формула Качанова
Для 3d пространства A=2.5.
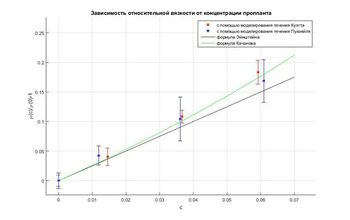
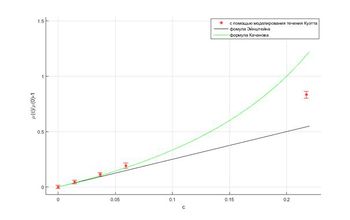
Для определения вязкости с помощью компьютерного эксперимента было проведено моделирование течений Пуазейля и Куэтта.

Заключение

• Разработана математическая модель смеси проппант-жидкостьна основе метода динамики частиц
• На основе математической модели написан комплекс программ на языке C++, позволяющий моделировать течение смеси проппант-жидкость
• Предложен способ определения эффективной вязкости смеси в зависимости от концентрации проппанта
• Проведено моделирование течения смеси в канале постоянного сечения при объемных концентрациях проппанта до 25%. При низких концентрациях определена зависимость эффективной вязкости смеси от концентрации проппанта.
• Проведено сравнение с аналитическими решениями – формулами для эффективной вязкости, предложенными Эйнштейном и Качановым
• Исследована сходимость решения по числу частиц при некоторых значениях концентрации проппанта

Список литературы

• Арбузов В. Н. Эксплуатация нефтяных и газовых скважин. Томский политехнический университет., 2011.
• J.J. Monaghan, "An introduction to SPH", Computer Physics Communications, vol. 48, pp. 88–96, 1988.
• V.A. Kuzkin, A.M. Krivtsov, A.M. Linkov, "Computer Simulation of Effective Viscosity of Fluid–Proppant Mixture Used in Hydraulic Fracturing", 2014, published in Fiziko-Tekhnicheskie Problemy Razrabotki Poleznykh Iskopaemykh, 2014, No. 1, pp. 3–12.
• V.A. Kuzkin, A.M. Krivtsov, A.M. Linkov, "Comparative Study of Rheological Properties of Suspensions by Computer Simulation of Poiseuille and Couette Flows", 2014, published in Fiziko-Tekhnicheskie Problemy Razrabotki Poleznykh Iskopaemykh, 2014, No. 6, pp. 23–32.
• BL Holian, DJ Evans "Shear viscosities away from the melting line: A comparison of equilibrium and nonequilibrium molecular dynamics" J. Chem. Phys. 78, 5147 (1983).
• Krivtsov, A.M., Deformirovanie i razrushenie tverdykh tel s mikrostrukturoi (Deformation and Failure of Microstructure Solids), Moscow: Fizmatlit, 2007.
• Verlet, L., Computer "Experiments" on Classical Fluids. I. Thermodynamical Properties of Lennard–Jones Molecules, Phys. Rev., 1967, vol. 159.
• Adachi J., Siebrits E., Peirce A., Desroches J. Computer simulation of hydraulic fractures, Int. J. Rock Mech. Min. Sci., 2007, vol. 44
• Linkov A.M. On efficient simulation of hydraulic fracturing in terms of particle velocity, Int. J. Eng. Sci., 2012, vol. 52
• A. Einstein, A new determination of molecular dimensions, Ann. Phys. 19 (4) (1906) 289–306. Correction: A. Einstein, A new determination of molecular dimensions, Ann. Phys. 34 (1911) 591–592.
• Brady, J.F., The Einstein Viscosity Correction in n Dimensions, Int. J. Mult. Flow, 1983, vol. 10.
• Rutgers Ir.R. Relative viscosity of suspensions of rigid spheres in Newtonian liquids, Rheol. Acta 2, 1962a, pp. 202–210
• Rutgers Ir.R. Relative viscosity and concentration, Rheol. Acta 2, 1962b, pp. 305–348
• Thomas D.G. 1965 Transport characteristics of suspension: 8. A note on the viscosity of Newtonian suspensions of uniform spherical particles, J. Colloid Sci. 20, pp. 267–277.
• Mueller S., Llewellin E.W., Mader H.M. The rheology of suspensions of solid particles, Proc. R. Soc. A, 2010, 466, pp. 1201–1228.
• Abedian, B. and Kachanov, M.L., On the Effective Viscosity of Suspensions, Int. J. Eng. Sci., 2010, vol. 48
• Зайдель А. Н. Элементарные оценки ошибок измерений, 1968, Изд. 3-е, испр. и доп. Изд-во «Наука», Ленингр. ютд., Л., 1—96.