Интегрирование вращательных степеней свободы с использованием тензора-интегратора Жилина
Команда проекта
- Исполнитель: Ковалев Олег
- Научный руководитель: Кузькин Виталий
Постановка задачи
- Интегрирование вращательного движения частицы, при моментном взаимодействии, с использованием тензора Жилина
Решение
Рассмотрим две частицы. К каждой из частиц жестко привяжем по вектору, которые в положения равновесия сонаправлены (вообще говоря, это условие необязательное) и сообщим начальные угловые скорости. Предположим, что момент, действующий на одну частицу, со стороны другой, есть функция этих самых векторов (например, векторное произведение данных векторов). Далее требуется определить новые положения векторов, связанных с частицами. Для этого требуется проинтегрировать уравнения движения для данных частиц. Значение угловой скорости получаем из второго уравнения динамики, значение угла поворота из соотношения, связывающего скорость изменение угла с угловой скоростью частицы.
Далее, пользуясь тензором поворота Эйлера, находим новые координаты векторов, связанных с частицами.
Результаты
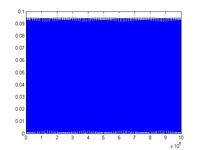
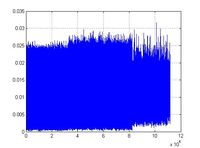
При использовании данного метода интегрирования, исследовался вопрос о сохранении энергии системы. Были построены графики зависимости энергии от времени (1 000 000 шагов) для различных систем частиц (Рис. 2: Energy (translational rotational), Рис. 4: Energy (rotational)). Как видно из графиков, энергия не возрастает.
Литература
- Рациональная механика сплошных сред. П. А. Жилин.