Динамическая потеря устойчивости цепочки частиц, соединенных линейными пружинами и имеющими изгибную жесткость
Курсовой проект по Механике дискретных сред
Исполнитель: Барсуков Севастьян
Группа: 3630103/60101
Семестр: осень 2019
Содержание
Постановка задачи
Исследовать динамическую потерю устойчивости цепочки частиц, соединенных линейными пружинами и имеющими изгибную жесткость при различных начальных отклонениях, а также при различных скоростях последней частицы.
Построение модели
В данной работе моделирование цепочки проводится методом динамики частиц.
Уравнение движения:
Метод решения
Для решения задачи использовался метод Верле (leapfrog):
Начальные условия
Частицы обладают случайными начальными вертикальными смещениями:
Граничные условия
Левый конец цепочки закреплен, правому задана постоянная скорость.
Параметры системы
Для проведения моделирование задаются следующие параметры: масса частиц , жесткость угловой пружины , количество частиц в цепочке
Взаимодействия в системе
В системе имеется два типа взаимодействия:
1. Потенциал линейной пружины:
Частицы соединены линейной пружиной:
где k - линейная жесткость пружины; r – расстояние между частицами.
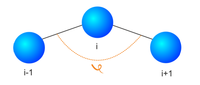
2. Потенциал угловой пружины:
Частицы соединены угловой пружиной, как показано на рис. 1:
где Cs – жесткость, φ – угол образованный 2-мя соседними связями.
Модель
В данной программе в начальный момент времени задаются:
- - жесткость угловой пружины
- - жесткость линейной пружины
- - начальное вертикальное смещение
- Возможность придания скорости левой частице
Текст программы на языке JavaScript:
1 window.addEventListener("load", program_code, false);
2 function program_code() {
3 var ctx = canvas_example.getContext("2d");
4 var w = canvas_example.width;
5 var h = canvas_example.height;
6 ctx.strokeRect(0,0,w,h);
7 //var ctx1 = canvas_example1.getContext("2d");
8 //var w1 = canvas_example1.width;
9 //var h1 = canvas_example1.height;
10 //ctx1.strokeRect(0,0,w1,h1);
11
12 var v0 = 10; //Скорость правого шарика
13 var v01 = 0; //Скорость левого шарика
14 var m = 10; //Масса шарика
15 var ht = 20; //параметр рисования
16 var htt = 40; //параметр рисования
17 var Cs = 10000; //Жесткость на изгиб
18 var rad = 5; //Радиус шариков
19 var dt = 0.01;
20 var tt = 0; // Время
21 var dy=document.getElementById('r3'); //Начальные смещения по оси y, задаваемые пользователем
22 var ppp2=document.getElementById('text3');
23 ppp2.innerHTML=dy.value;
24 dy.oninput = function() {
25 ppp2.innerHTML="<"+dy.value;
26 for (var i=0;i<u_len;i++){
27 Yt[i] = dy.value*Math.random()+h/2;
28 }
29 Yt[0] = h/2;
30 Yt[u_len-1] = h/2;
31 r_ = [Xt,Yt];
32 defaultdraw();
33 }
34 var F_ = [0,0];
35 var pp = [0,0];
36 var FF = [];
37 var v = [[v01,0,0,0,0,0,0,0,0,v0],[0,0,0,0,0,0,0,0,0,0]]; //массив скоростей
38 var kk = -5; //Жесткость пружины
39 var Xt = [w/11,2*w/11,3*w/11,4*w/11,5*w/11,6*w/11,7*w/11,8*w/11,9*w/11,10*w/11]; //начальные положения частиц по оси X
40 var u_len = Xt.length;
41 var Yt = []; //Начальные смещения по оси y
42 for (var i=0;i<u_len;i++){
43 Yt[i] = 1*Math.random()+h/2;
44 }
45 Yt[0] = h/2; //Граничные условия
46 Yt[u_len-1] = h/2;
47 var r_ = [Xt,Yt]; //Вектор перемещений
48 var r12_ = [[0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0]]; //Вектор между частицами
49 var r12 = [0,0,0,0,0,0,0,0,0]; //Модуль вектора перемещений
50
51 // Рисование в начальном положении
52 function defaultdraw(){
53 ctx.clearRect(0,0,w,h);
54 ctx.strokeRect(0,0,w,h);
55 for (var i=0;i<u_len;i++){
56 ctx.beginPath();
57 ctx.arc(Xt[i],Yt[i],rad,0,Math.PI*2);
58 ctx.fill();
59 }
60 for (var i=0;i<u_len-1;i++){
61 var x_st = r_[0][i]
62 var y_st = r_[1][i]
63 var x_end = r_[0][i+1]
64 var y_end = r_[1][i+1]
65 var l = r_[0][i+1] - r_[0][i];
66 var ly = r_[1][i+1] - r_[1][i]
67 ctx.beginPath();
68 ctx.bezierCurveTo(x_st, y_st, x_st + l / 4, y_st + ly / 4 + ht, x_st + l / 2, y_st + ly / 2);
69 ctx.bezierCurveTo(x_st + l / 2, y_st + ly / 2, x_st + 3 * l / 4, y_st + 3 * ly / 4 - ht, x_st + l, y_st + ly);
70 ctx.stroke();
71 }
72 for (var i=0;i<u_len-2;i++){
73 var x_st = r_[0][i]
74 var y_st = r_[1][i]
75 var x_end = r_[0][i+1]
76 var y_end = r_[1][i+1]
77 var x_end_end = r_[0][i+1]
78 var y_end_end = r_[1][i+1]
79 var l = r_[0][i+1] - r_[0][i]
80 var ly = r_[1][i+1] - r_[1][i]
81 var l1 = r_[0][i+2] - r_[0][i+1]
82 var ly1 = r_[1][i+2] - r_[1][i+1]
83 ctx.beginPath();
84 ctx.bezierCurveTo(x_st+l/2, y_st+ly/2, x_st + l, y_st+ly+htt , x_st+l + l1/2, y_st +ly+ ly1/2);
85 ctx.stroke();
86 }
87 }
88 defaultdraw();
89
90 var Css=document.getElementById('r1'); //Задаваемая угловая жесткость
91 var ppp=document.getElementById('text');
92 var k1=document.getElementById('r2'); //Задаваемая жесткость
93 var ppp1=document.getElementById('text2');
94 ppp.innerHTML=Css.value;
95 ppp1.innerHTML=-k1.value;
96 Css.oninput = function() {
97 ppp.innerHTML=Css.value;
98 }
99 k1.oninput = function() {
100 ppp1.innerHTML=-k1.value;
101 }
102
103 // Физический модуль
104 function physics() {
105 chbox=document.getElementById('one'); // Будет ли скорость у левой частицы
106 if (chbox.checked) {
107 v01 = v0
108 }
109 else {
110 v01 = 0
111 }
112
113 Cs = Css.value
114 kk = k1.value
115 for (var i=0;i<u_len-1;i++){
116 r12_[0][i] = r_[0][i+1]-r_[0][i];
117 r12_[1][i] = r_[1][i+1]-r_[1][i];
118 }
119 for (var i=0;i<u_len-1;i++){
120 r12[i] = Math.sqrt(r12_[0][i]*r12_[0][i]+r12_[1][i]*r12_[1][i]);
121 }
122 f = []
123 for (var i=0;i<2;i++){
124 f[i] = []
125 for (var j=0;j<u_len;j++){
126 f[i][j] = 0
127 }
128 }
129 for (var i=0;i<u_len-2;i++){
130 F_[0] = kk*((w/(u_len+1))-r12[i])*(r12_[0][i]/r12[i])
131 F_[1] = kk*((w/(u_len+1))-r12[i])*(r12_[1][i]/r12[i])
132
133 etta = -(r12_[0][i]*r12_[0][i+1]+r12_[1][i]*r12_[1][i+1]) / ( r12[i]*r12[i+1] );
134 phi = Math.acos(etta);
135 Fp = [0,0];
136 Fn = [0,0];
137 F = [0,0];
138 if (phi != Math.PI){
139 koef = Cs * (Math.PI - phi)/(Math.sqrt(1-etta*etta) * r12[i] * r12[i+1]);
140 A = [[ 1 - Math.pow(r12_[0][i]/r12[i],2), -r12_[0][i]*r12_[1][i]/(r12[i]*r12[i])], [-r12_[0][i]*r12_[1][i]/(r12[i]*r12[i]), 1 - Math.pow(r12_[1][i]/r12[i],2) ]];
141 B = [[ 1 - Math.pow(r12_[0][i+1]/r12[i+1],2), -r12_[0][i+1]*r12_[1][i+1]/(r12[i+1]*r12[i+1])],[ -r12_[0][i+1]*r12_[1][i+1]/(r12[i+1]*r12[i+1]), 1 - Math.pow(r12_[1][i+1]/r12[i+1],2) ]];
142 Fp = [-koef*(r12_[0][i+1]*A[0][0]+r12_[1][i+1]*A[1][0]),-koef*(r12_[0][i+1]*A[0][1]+r12_[1][i+1]*A[1][1])];
143 Fn = [koef*(r12_[0][i]*B[0][0]+r12_[1][i]*B[1][0]),koef*(r12_[0][i]*B[0][1]+r12_[1][i]*B[1][1])];
144 F = [-Fn[0] - Fp[0],-Fn[1] - Fp[1]];
145 }
146 f[0][i] = f[0][i] + F_[0] + Fp[0];
147 f[1][i] = f[1][i] + F_[1] + Fp[1];
148 f[0][i+1] = f[0][i+1]-F_[0]+F[0];
149 f[1][i+1] = f[1][i+1]-F_[1]+F[1];
150 f[0][i+2] = f[0][i+2]+Fn[0];
151 f[1][i+2] = f[1][i+2]+Fn[1];
152 }
153 pp[0] = kk*((w/(u_len+1))-r12[u_len-2])*(r12_[0][u_len-2]/r12[u_len-2])
154 pp[1] = kk*((w/(u_len+1))-r12[u_len-2])*(r12_[1][u_len-2]/r12[u_len-2])
155 f[0][u_len-2] = f[0][u_len-2] +pp[0];
156 f[1][u_len-2] = f[1][u_len-2] +pp[1];
157 f[0][u_len-1] = f[0][u_len-1]-pp[0];
158 f[1][u_len-1] = f[1][u_len-1]-pp[1];
159 for (var i=0;i<u_len-1;i++){
160 v[0][i] = v[0][i] + (f[0][i]/m) * dt;
161 v[1][i] = v[1][i] + (f[1][i]/m) * dt;
162 }
163
164
165 v[0][0] = v01;
166 v[1][0] = 0;
167 v[0][u_len-1] = -v0;
168 v[1][u_len-1] = 0;
169 for (var i=0;i<u_len;i++){
170 r_[0][i] = r_[0][i] + v[0][i] * dt;
171 r_[1][i] = r_[1][i] + v[1][i] * dt;
172 }
173 }
174 //Модуль рисования
175 function draw() {
176 tt=tt+1
177 // Условия остановки выполнения программы
178 if ((tt>6300) && (v01==0)){
179 clearInterval(tim)
180 }
181 if ((tt>3150) && (v01!=0)){
182 clearInterval(tim)
183 }
184 ctx.clearRect(0,0,w,h);
185 ctx.strokeRect(0,0,w,h);
186 // Рисование шариков
187 for (var i=0;i<u_len;i++){
188 ctx.beginPath();
189 ctx.arc(r_[0][i],r_[1][i],rad,0,Math.PI*2);
190 ctx.fill();
191 }
192 //if ((tt%10==0){
193 FF.push(f[0][u_len-1])
194 //}
195 if (tt==60){
196 console.log(JSON.stringify(FF))
197 }
198 // График силы
199 //for (var i=0;i<u_len;i++){
200 // ctx1.beginPath();
201 // ctx1.arc(tt/10,-f[0][u_len-1]/10+h/2,1,0,Math.PI*2);
202 // ctx1.stroke();
203 //}
204 ctx.beginPath();
205 for (var i=0;i<u_len-1;i++){
206 var x_st = r_[0][i]
207 var y_st = r_[1][i]
208 var x_end = r_[0][i+1]
209 var y_end = r_[1][i+1]
210 var l = r_[0][i+1] - r_[0][i];
211 var ly = r_[1][i+1] - r_[1][i]
212 ctx.beginPath();
213 ctx.bezierCurveTo(x_st, y_st, x_st + l / 4, y_st + ly / 4 + ht, x_st + l / 2, y_st + ly / 2);
214 ctx.bezierCurveTo(x_st + l / 2, y_st + ly / 2, x_st + 3 * l / 4, y_st + 3 * ly / 4 - ht, x_st + l, y_st + ly);
215 ctx.stroke();
216 }
217 for (var i=0;i<u_len-2;i++){
218 var x_st = r_[0][i]
219 var y_st = r_[1][i]
220 var x_end = r_[0][i+1]
221 var y_end = r_[1][i+1]
222 var x_end_end = r_[0][i+1]
223 var y_end_end = r_[1][i+1]
224 var l = r_[0][i+1] - r_[0][i]
225 var ly = r_[1][i+1] - r_[1][i]
226 var l1 = r_[0][i+2] - r_[0][i+1]
227 var ly1 = r_[1][i+2] - r_[1][i+1]
228 ctx.beginPath();
229 ctx.bezierCurveTo(x_st+l/2, y_st+ly/2, x_st + l, y_st+ly+htt , x_st+l + l1/2, y_st +ly+ ly1/2);
230 ctx.stroke();
231 }
232 ctx.closePath();
233 }
234 // Контрольный модуль
235 function control(){
236 physics();
237 draw();
238 }
239 var tim;
240 // Функция остановки программы
241 function go1(){
242 clearInterval(tim);
243 }
244 // Функция работы программы
245 function go(){
246 clearInterval(tim);
247 control() ;
248 tim = setInterval(control,1000/60);
249 }
250 button_aler.onclick=go //Кнопка старта
251 button_aler1.onclick=go1 //Кнопка остановки
252 }