Курсовые работы 2018-2019 учебного года >
Изгиб балки c V-model взаимодействием
Курсовой проект по Механике дискретных сред
Исполнитель: Абрамов Игорь
Группа: 43604/1
Семестр: осень 2018
Постановка задачи
Создание модели и визуализация изгиба балки с V-model взаимодействием.
Решение
Балка моделируется как система частиц, каждая из которых взаимодействует с двумя ближайшими соседями.
Для ориентация каждой [math]i-[/math]ой частицы в пространстве используется жёстко связанный с ней в центре частицы базис [math]\mathbf{n}_{i1}, \mathbf{n}_{i2}, \mathbf{n}_{i3}[/math].
Также введём два вектора
[math] \mathbf{r}_{ij}=\mathbf{r}_i - \mathbf{r}_j [/math]
[math] \mathbf{e}_{ij} = \mathbf{r}_{ij} / r_{ij} [/math]
Вектор [math]\mathbf{D}_{ij}[/math] - соединяет базисы, связанные с соответствующими частицами, поэтому в данной постановке
он равен [math]\mathbf{r}_{ij}[/math]. Вектор [math]\mathbf{e}_{ij} = \mathbf{r}_{ij} / r_{ij}[/math] - единичный, сонаправленный [math]\mathbf{r}_{ij}[/math].
Потенциальная энергия связи:
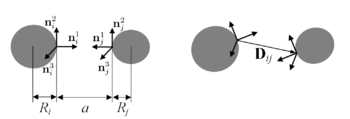
Взаимодействие двух частиц
[math]
U = \frac{B_1}{2}(D_{ij}-a)^2 + \frac{B_2}{2}(\mathbf{n}_{j1}-\mathbf{n}_{i1})\cdot\mathbf{d}_{ij}
+ B_3 \mathbf{n}_{i1}\cdot\mathbf{n}_{j1} - \frac{B_4}{2}(\mathbf{n}_{i2}\cdot\mathbf{n}_{j2} + \mathbf{n}_{i3}\cdot\mathbf{n}_{j3})
[/math]
Таким образом, уравнения для сил и моментов принимают следующий вид:
[math]
\mathbf{M}^{TB} = B_3 \mathbf{n}_{j1} \times \mathbf{n}_{i1} - \frac{B_4}{2}(\mathbf{n}_{j2}\times\mathbf{n}_{i2} + \mathbf{n}_{j3}\times\mathbf{n}_{i3})
[/math]
[math]
\mathbf{F}_{ij} = B_1(r_{ij}-a)\mathbf{r}_{ij} + \frac{B_2}{2r_{ij}}(\mathbf{n}_{j1} - \mathbf{n}_{i1}
-\mathbf{e}_{ij}\cdot(\mathbf{n}_{j1} - \mathbf{n}_{i1})\mathbf{e}_{ij})
[/math]
[math]
\mathbf{M}_{ij} = -\frac{B_2}{2}\mathbf{e}_{ij}\times\mathbf{n}_{i1} + \mathbf{M}^{TB}
[/math]
[math]
\mathbf{M}_{ji} = \frac{B_2}{2}\mathbf{e}_{ij}\times\mathbf{n}_{j1} - \mathbf{M}^{TB}
[/math]
Для балки с короткими связями между частицами параметры модели принимают следующие значения:
[math]
B_1 = \frac{ES}{a}
[/math]
[math]
B_2 = -\frac{2EJ[kAa^2-12J(1+\nu)]}{a[kSa^2+24J(1+\nu)]}
[/math]
[math]
B_3 = \frac{6kSEJa}{kSa^2+24J(1+\nu)}
[/math]
[math]
B_4 = \frac{GJ_p}{a}
[/math]
Ссылки
