Моделирование поведения толпы методом клеточных автоматов
Курсовой проект по Механике дискретных сред
Исполнитель: Бальцер Анастасия
Группа: 43604/1
Семестр: осень 2018
Проблема поведения толпы
Толпа – бесструктурное скопление нескольких существ в некотором объеме, лишенных ясно осознаваемой общности целей, но взаимно связанных сходством эмоционального состояния и общим объектом внимания. Участниками толп могут являться любые существа, способные передвигаться и принимать решения о направлении своего дальнейшего движения. Очевидно, что индивидуальное поведение человека вне толпы обуславливается множеством высокоуровневых факторов, связанных с его интеллектуальной деятельностью. Но с другой стороны, человек внутри толпы теряет свою индивидуальность и начинает подчиняться более простым законам поведения. Таким образом, толпа образом начинает приобретать новые качества, которые не являются характерными для отдельных независимых ее участников. Главная задача моделирования толпы – описание поведения множества индивидов в определенных условиях.
Постановка задачи
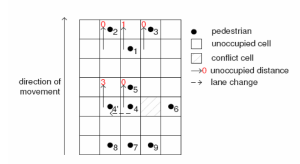
Существует множество подходов к созданию моделей поведения толпы, одним из простейших методов моделирования является подход на основе клеточных автоматов. В подобных подходах пространство, по которому перемещаются агенты, представляется в виде набора клеток, образующих периодическую решетку с заданными правилами перехода. Данные правила определяют состояние клетки в следующий момент времени через состояние клеток, находящихся от нее на определенном расстоянии в текущий момент времени.
Решение
Существует множество модификаций метода, в данной работе была выбрана модификация, полученная V.J.Blue, J.L.Adler, где пешеходная зона моделируется в замкнутой областью с шириной , длиной , . Каждой клетке присвоено значение , , . Плотность толпы рассчитывается в начале и остается постоянной. Время дискретно , i = 1, 2, ... T. Изменение ряда и обновление скорости происходит в 4 этапа: 1. Конфигурация изменения дорожек изменяет положение каждого "пешехода", находящегося на сетке 2. Пешеходы перемещаются в предписанные правилом места 3. Находим допустимую скорость каждого, основываясь на зазоре впереди и желаемой скорости пешехода 4. Пешеход двигается с рассчитанной допустимой скоростью
При этом положим, что два соседних пешехода не могут столкнуться. Дорожка выбирается, так чтобы движение вперед было максимальным, рассчитывая возможный пустой промежуток впереди пешехода.
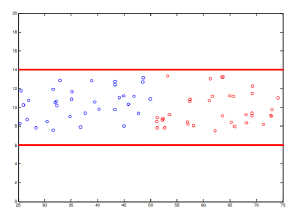
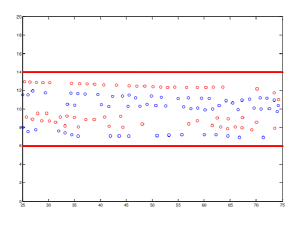
Был смоделирован поток людей идущих навстречу по коридору:
Результаты представляют собой некий идеализированный поток, в реальном потоке людей нет однородности, часто пешеходы с большей скоростью, обгоняют тех, кто идет медленнее. В случаях если плотность потока очень большая такие маневры отдельных пешеходов приводят к сбою концепции "дорожек", поэтому данная модель для описания таких потоков не годится.
Источники
Cellular automata microsimulation for modeling bi-directional pedestrian walkways