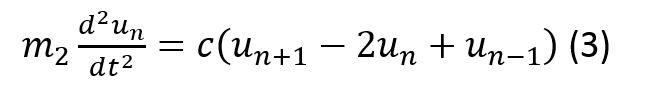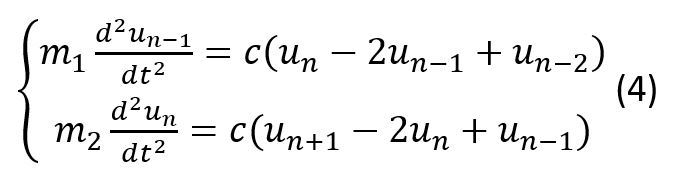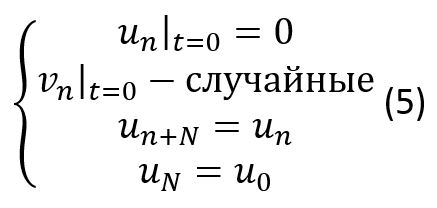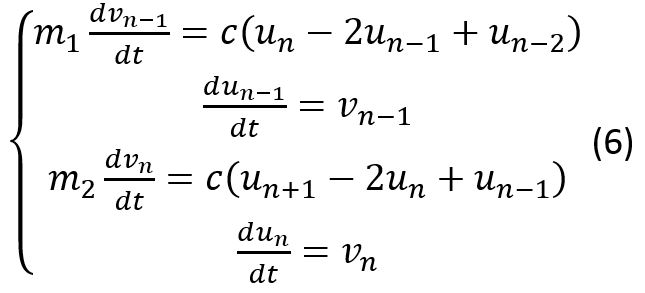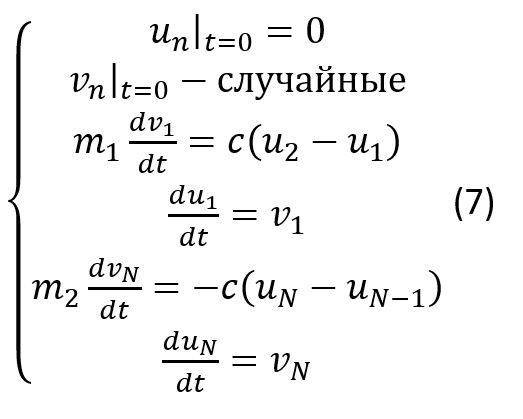Перераспределение энергии между степенями свободы в нелинейной двухатомной цепочке

Постановка задачи

Рассмотреть перераспределение энергии между степенями свободы в нелинейной двухатомной цепочке, построить графики зависимости энергии частиц от времени.

Решение

Рассмотрим модель колебаний одномерной двухатомной цепочки массами m1 и m2. Пусть в этой цепочке находится N атомов. Обозначим смещение n-го атома un, а атома, отстоящего от него на p узлов, – un+p. Примем в качестве положительных смещения атомов вправо от положения равновесия, а отрицательных – влево.

Каждый атом смещается только вдоль цепочки, что следует из требования одномерности модели. Пусть атомы связаны между собой упругой силой F с коэффициентом упругости с. Найдем уравнение движения n-го и n+1-го атома в цепи. В равновесном положении силы, действующие на атомы, равны нулю. При произвольных смещениях на каждый n-й атом будет действовать сила со стороны соседних атомов. Суммарную силу, действующую на n-й атом со стороны соседних атомов, можно представить в виде:
[math] F_n=F_{n,n+1}-F_{n-1,n}=c(u_{n+1}-2u_n+u_{n-1}) (1) [/math]
Запишем систему уравнений движения атомов массой [math] m_{1} [/math] и [math] m_{2} [/math]
[math] m_{1} \frac{d^2 u_{2n-1}}{dt^2}=c(u_{2n}-2u_{2n-1}+u_{2n-2}) [/math]
[math] m_{2} \frac{d^2 u_{2n}}{dt^2}=c(u_{2n+1}-2u_{2n}+u_{2n-1}) [/math]
Уравнение движения n-го атома под действием силы F_n выглядит следующим образом:

Аналогичное уравнение записывается для частиц с массой m1. Таким образом получим систему уравнений:

В качестве начальных условий заданы случайные начальные скорости таким образом, что средняя скорость всех частиц равна 0. Перемещения всех частиц в начальный момент времени равны нулю. Также заданы периодические граничные условия на перемещения.

От системы (4) с начальными и граничными условиями (5) мы перешли к системе (6, 7):

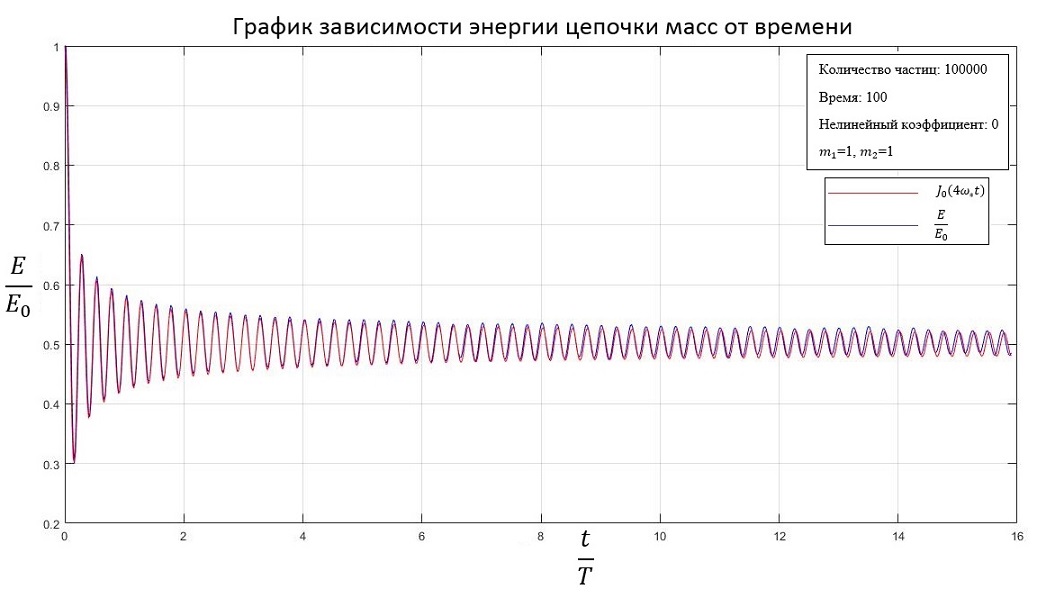
Система (6) решалась в Matlab методом конечных разностей. В задаче на каждом шаге по времени находилась кинетическая энергия всей системы, после чего был построен график зависимости энергии системы от времени. Для частиц одинаковой массы был получен следующий график:

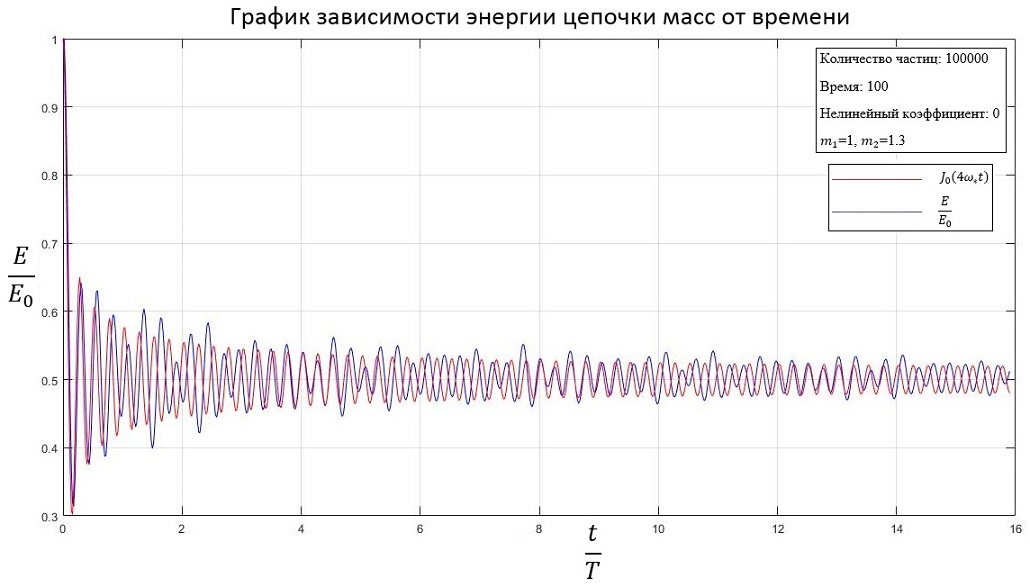
Если рассматривать частицы разной массы, то график зависимости будет иметь следующий вид (m1=1, m2=1.3):

Рассмотрим нелинейную постановку задачи. В выражении для силы будет присутствовать слагаемое третьего порядка:

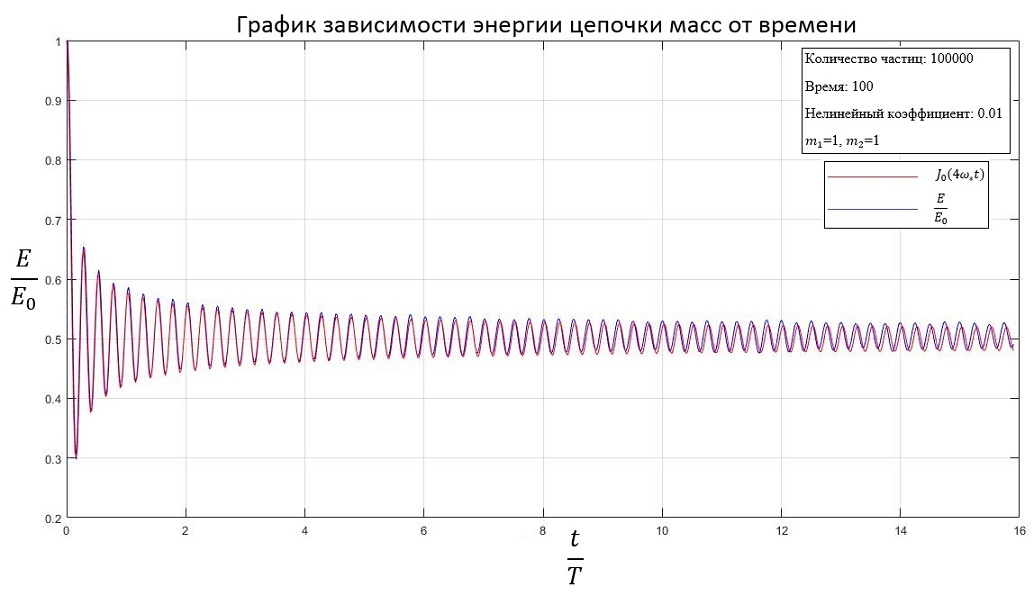
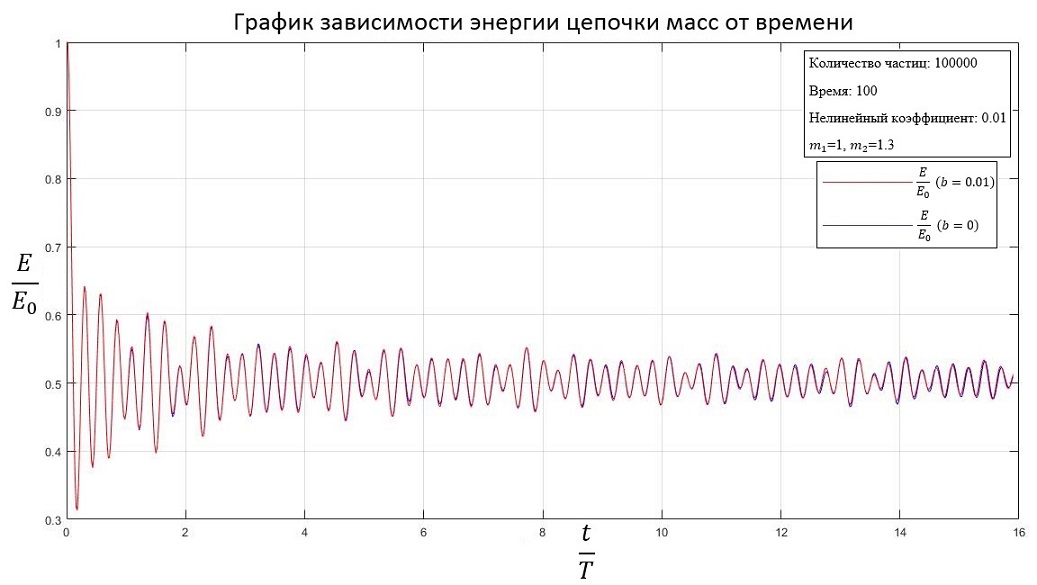
Решается данная задача в нелинейной постановке аналогичным образом. если мы возьмем нелинейный коэффициент b равным нулю, получим решение, соответствующее предыдущей задаче. Начнем постепенно увеличивать коэффициент b и заметим, что система начнет затухать быстрее. При одинаковой массе частиц: b=0.01

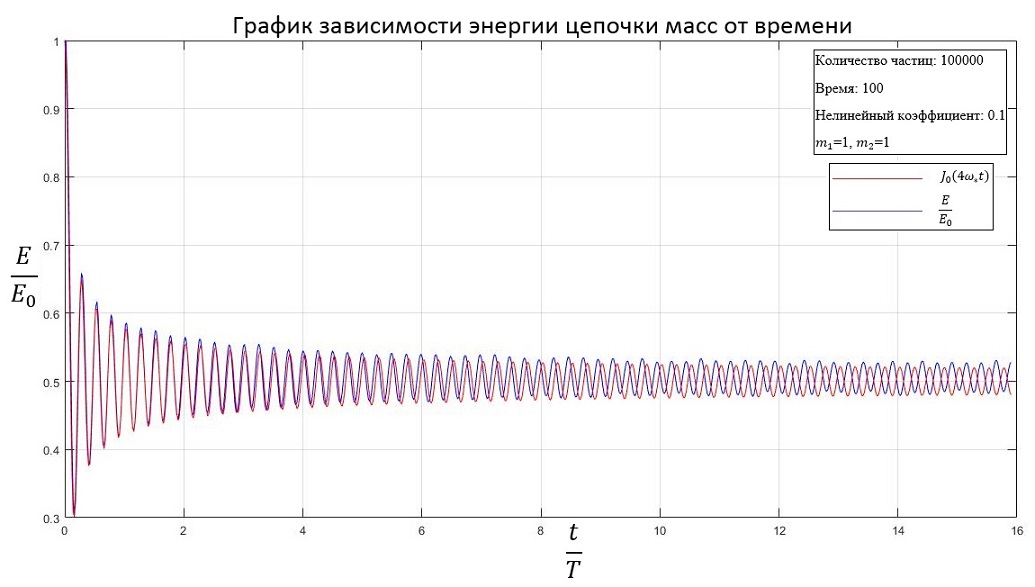
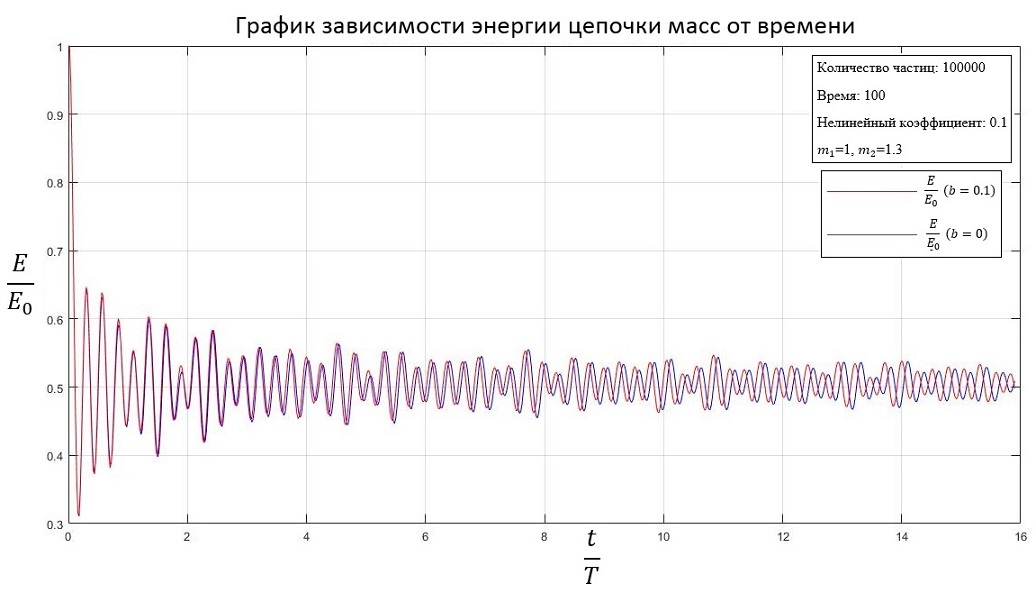
b=0.1

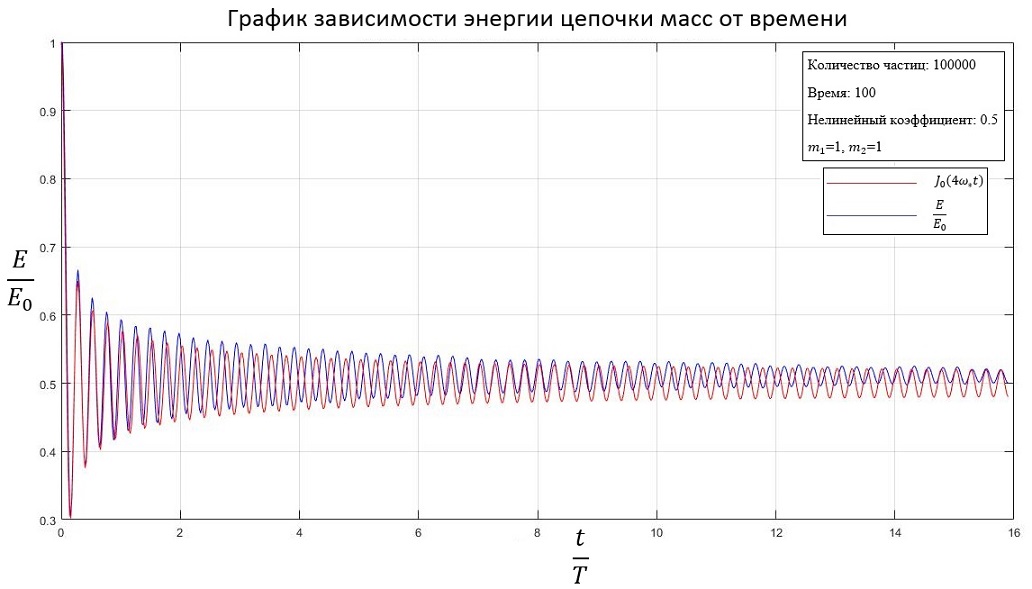
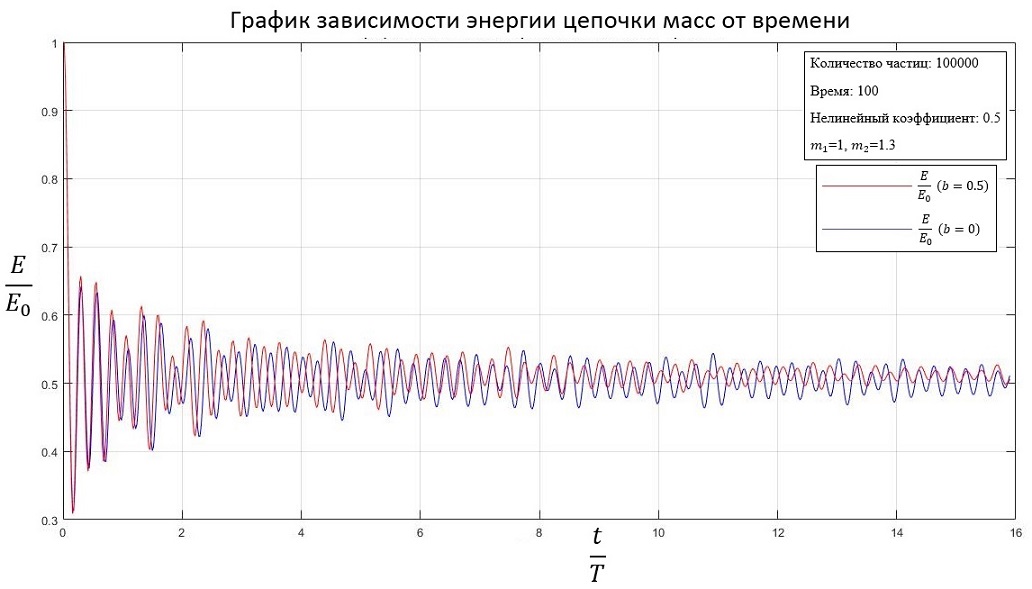
b=0.5

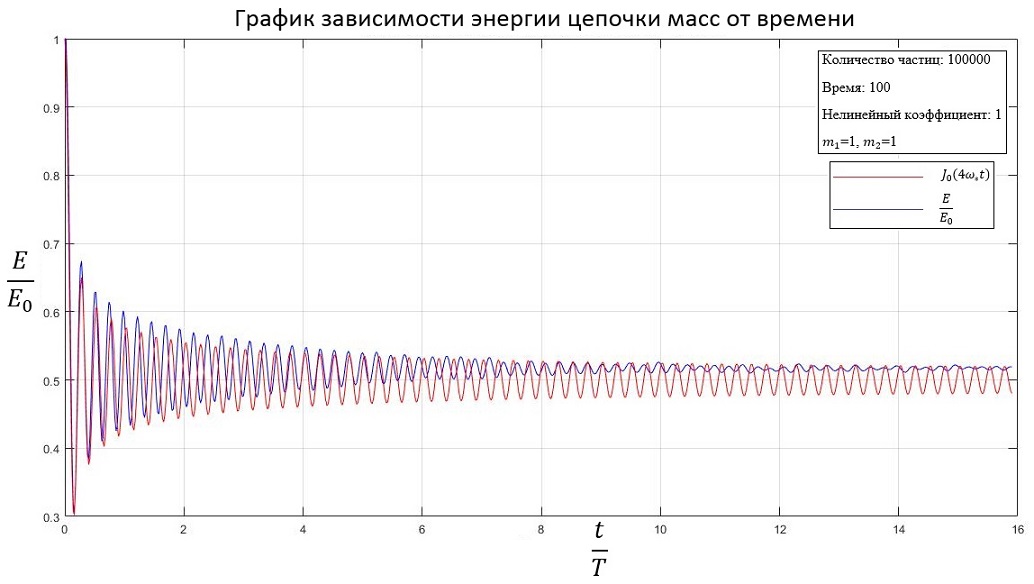
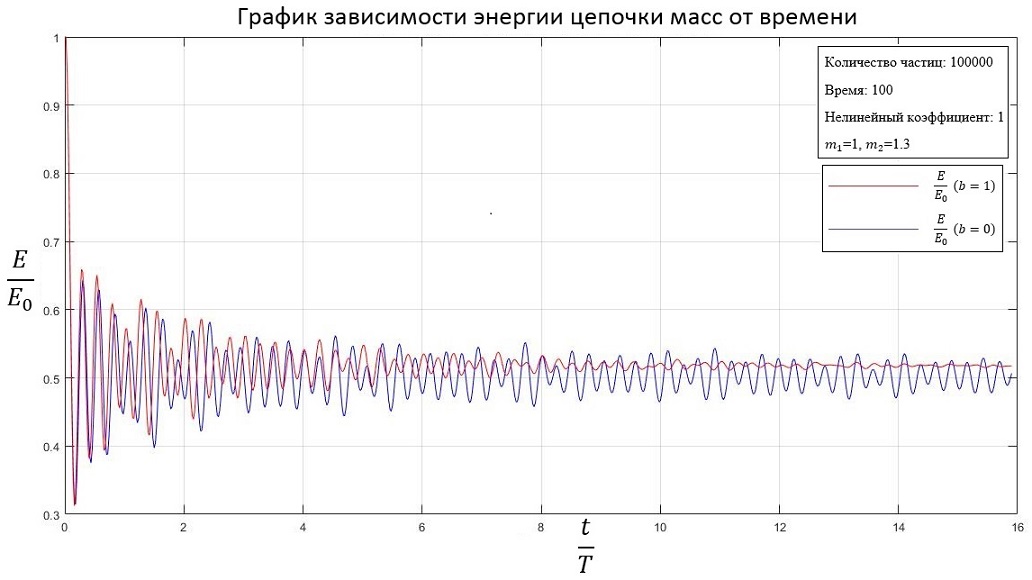
b=1

Разные массы частиц (m1=1, m2=1.3): b=0.01

b=0.1

b=0.5

b=1

Участники проекта

Белоусова Екатерина

См. также

Кафедра "Теоретическая механика"