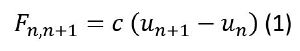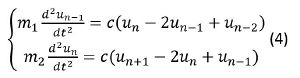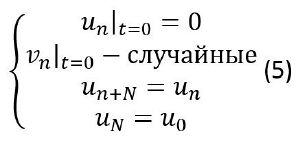Перераспределение энергии между степенями свободы в нелинейной двухатомной цепочке

Постановка задачи

Рассмотреть перераспределение энергии между степенями свободы в нелинейной двухатомной цепочке, построить графики зависимости энергии частиц от времени.

Решение

Рассмотрим модель колебаний одномерной двухатомной цепочки массами m1 и m2. Пусть в этой цепочке находится N атомов. Обозначим смещение n-го атома un, а атома, отстоящего от него на p узлов, – un+p. Примем в качестве положительных смещения атомов вправо от положения равновесия, а отрицательных – влево (рис.1).

Каждый атом смещается только вдоль цепочки, что следует из требования одномерности модели. Пусть атомы связаны между собой упругой силой F с коэффициентом упругости с. Найдем уравнение движения n-го и n+1-го атома в цепи. В равновесном положении силы, действующие на атомы, равны нулю. При произвольных смещениях на каждый n-й атом будет действовать сила со стороны соседних атомов. В соответствии с элементарным законом Гука эту силу можно представить в виде:

Тогда суммарная сила, действующая на n-й атом со стороны соседних атомов, будет:

Уравнение движения n-го атома под действием силы F_n выглядит следующим образом:

Аналогичное уравнение записывается для частиц с массой m1. Таким образом получим систему уравнений:

В качестве начальных условий заданы случайные начальные скорости таким образом, что средняя скорость всех частиц равна 0. Перемещения всех частиц в начальный момент времени равны нулю. Также заданы периодические граничные условия на перемещения.