Цепочка частиц с чередующимися массами

Виртуальная лаборатория>Цепочка с чередующимися массами

---

Рассматривается цепочка, состоящая из частиц двух разных масс, соединенных одинаковыми пружинами. Уравнение движения имеет вид:

[math] \ddot{\bf u}_{n} = {\omega}_{0}^2({\bf u}_{n+1}-2{\bf u}_{n} + {\bf u}_{n-1}), [/math]

где [math] {\bf u}[/math] - перемещение, [math]{\omega}_{0} =\sqrt\frac {\bf c}{\bf m} [/math], [math] {\bf c}[/math] - жёсткость пружинок, [math] {\bf m}[/math] - масса частиц.

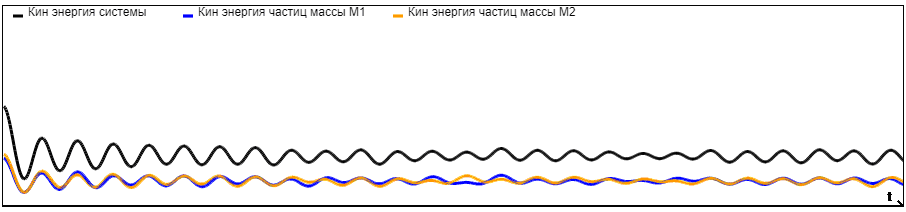
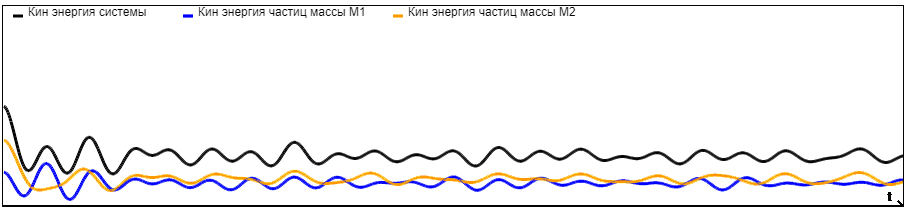
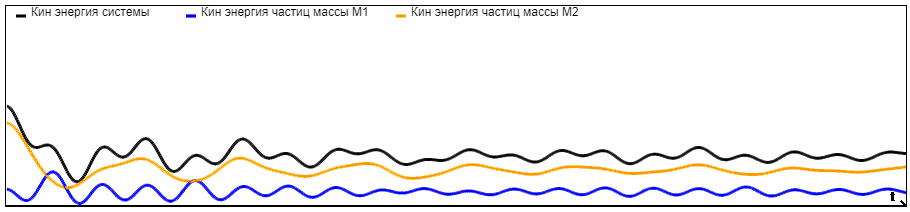
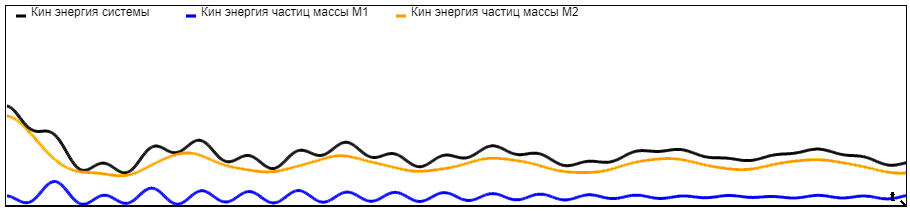
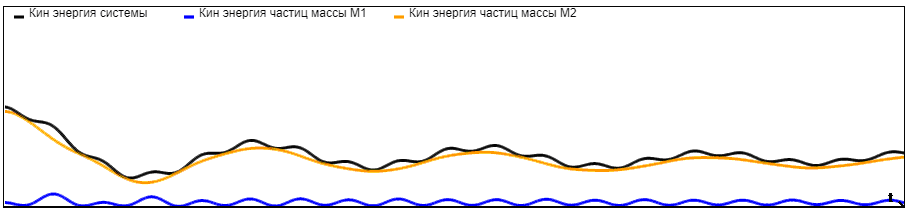
На графиках представлены зависимости кинетической энергии частиц с массой M1, кинетической энергии частиц с массой M2 и кинетической энергии системы от времени при разных отношениях масс. Количество частиц = 1000. Граничные условия - периодические.

При [math]\frac {\bf M2}{\bf M1}=1[/math]

При [math]\frac {\bf M2}{\bf M1}=2[/math]

При [math]\frac {\bf M2}{\bf M1}=5[/math]

При [math]\frac {\bf M2}{\bf M1}=10[/math]

При [math]\frac {\bf M2}{\bf M1}=20[/math]

Вывод:

Анализируя графики, можно сделать вывод, что с увеличением отношения M2/M1 возрастает и кинетическая энергия частиц с массой M2, следовательно, она начинает вносить больший вклад в кинетическую энергию системы, и на графиках мы видим ее приближение к кинетической энергии системы.