Исследование коэффициента сдвига в зависимости от параметров сечения стержня
БАКАЛАВРСКАЯ РАБОТА
Автор работы: Филимонов Александр
Научный руководитель: д.ф.-м.н., профессор Иванова Елена Александровна
Содержание
Введение[править]
Тонкостенные стержни — элементы конструкций и сооружений цилиндрической или призматической формы, у которых все три характерных измерения (толщина, наибольший размер поперечного сечения и длина) выражаются величинами различных порядков, т. е. первая значит, меньше второй, а вторая — меньше третьей [1]. Тонкостенные стержни находят широкое применение в строительных конструкциях (стальные и алюминиевые прокатные, составные и гнутые профили, железобетонные тонкостенные элементы, кессонные конструкции и т. п.), а также в машиностроении, самолетостроении и т. д. Различают тонкостенные стержни открытого профиля швеллер, двутавр и др. и закрытого профиля (напр., коробчатого). Тонкостенные стержни обычно рассматриваются при расчете как пространственные конструкции; специфика их работы связана с деформацией контура поперечного сечения. С точки зрения расчета тонкостенные стержни представляют собой оболочки. Методы расчета теории стержней основаны на предположении о недеформируемости контура поперечного сечения, которые и будут использоваться в данной работе. Стоит заметить, что модули жёсткости на растяжение, изгиб и кручение хорошо известны и приведены во всех справочниках [2]. Интерес представляет модуль жёсткости на поперечный сдвиг. Существует формула для коэффициента сдвига . Зависимость от и вопроса не вызывает, интерес представляет значение и его нахождение. Пользоваться будем моделью балки Тимошенко.
Цели данной работы[править]
Исследование коэффициентов сдвига прямолинейных тонкостенных стержней .
- определение коэффициентов сдвига на основании численного эксперимента.
- провести исследование влияния формы сечения стержня на коэффициент сдвига.
Метод определения упругих модулей[править]
В данной работе используется метод, основанный на решении статических задач. Этот метод основан на сравнении результатов решения трехмерных задач с результатами решения соответствующих задач теории стержней. Далее будем сравнивать кинематические характеристики. В результате решения трехмерной задачи получаем распределение перемещений по сечению стержня. Существуют различные подходы к определению соотношений между перемещениями трехмерного тела и перемещением и поворотом сечения стержня. Далее будет использоваться подход, согласно которому считается, что количество движения и кинетический момент стержня и трехмерного тела (прообраза) совпадают между собой. Проинтегрировав данное соотношение по времени, придем к следующим уравнениям: где - объемная плотность массы материала стержня, - вектор смещений точек трехмерной среды, - вектор положения точек поперечного сечения, - площадь поперечного сечения.
Постановка задачи для определения модуля жесткости на растяжение (тестовая задача)[править]
Рассматривается стержень длиной 𝑙. Один конец стержня жестко закреплен, то есть этот конец не может ни поворачиваться, ни перемещаться. На другой конец действует продольная сила .
- модуль жесткости на растяжение (получившаяся формула, на основании необходимости совпадения количества движения и кинетического момента у модели и у трёхмерного тела.
- хорошо известная формула для модуля жесткости, где Е - модуль Юнга, S - площадь поперечного сечения. Сравним результаты вычислений модуля жесткости по известной формуле и по полученной. Для этого введем относительную погрешность измерений 𝛿:
Решение соответствующей задачи строилось в пакете Abaqus. Рассматривался стержень длиной 𝑙 = 1м. Поперечное сечение стержня — П – образный профиль (швеллер) площадью . (Характерные размеры стрежня a(толщина) = 0.02м, b = 0.5м, c = 0.429.). Материал стержня — медь (модуль Юнга Па). Приложенная сила 𝑁 = 500кН. Вычисления проводились при количестве элементов 𝑛 = 14300. В результате решения было найдено . С учетом того, что .
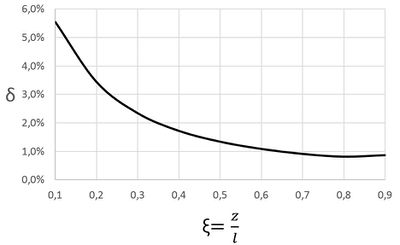
Построим график зависимости относительной погрешности величин и от безразмерной координаты сечения стержня ξ = z/l для рассматриваемого случая:
По этому графику видно, что чем дальше от заделки находится координата сечения, тем меньше погрешность между известной и полученной формулами.
Постановка задачи для определения коэффициента сдвига[править]
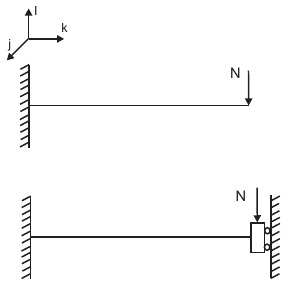
Рассматривается задача изгиба стержня длинной (см. Рис. 1). Один конец жестко закреплен, на втором конце действует поперечная сила .
Решение будем искать в виде: .
Имеем:
Здесь - перемещение стержня со свободным концом, - угол поворота сечения стержня со свободным концом, - модуль жесткости на поперечный сдвиг, - модуль жесткости на изгиб.
Решение содержит два неизвестных модуля упругости. Поэтому, чтобы получить формулу, где не будет изгибной жесткости, решается две задачи: изгиб стержня со свободным концом и с заделкой, как показано на Рис 2.
Угол поворота сечения и перемещение для стержня с двумя заделками: где - перемещение стержня с заделкой с двух сторон, - угол закручивания стержня с заделкой с двух сторон.
Переходим к относительной координате сечения, делая замену . Получаем итоговую формулу для модуля жесткости на поперечный сдвиг: Перейдем от найденного модуля жесткости на поперечный сдвиг к коэффициенту сдвига:
Здесь - модуль сдвига, - площадь поперечного сечения.
Результаты[править]
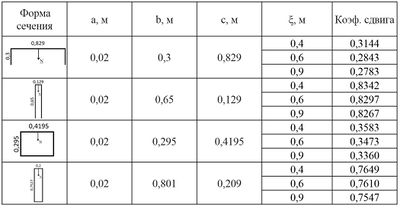
Несколько результатов экспериментов можно увидеть в таблице(Рис. 3).
По приведенным значениям в таблице видно, что коэффициент сдвига принимает различные значения. Можно также заметить, что чем меньше с — ширина наших сечений и чем больше длина сторон (b), тем ближе коэффициент сдвига к 1. Также стоит отметить, что коэффициент сдвига не зависит от позиции сечения.
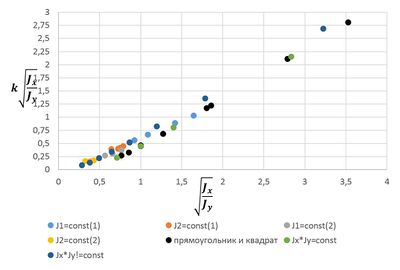
Также не стоит оставлять без внимания результат, полученный при нанесении всех результатов на график.
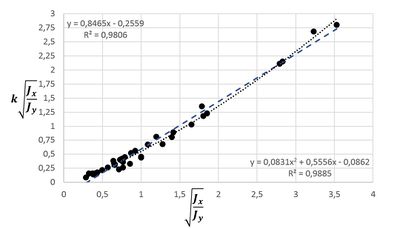
Было построено несколько зависимостей, но наиболее точно все эти точки аппроксимирует полином второй степени, изображенный на Рис. 5. Теперь приведем уравнение этой кривой к виду .
Получилось выражение для коэффициента сдвига, который можно найти, зная только два момента инерции.
Выводы[править]
В работе решен ряд задач численным методом по трехмерной теории. Основываясь на сравнении напряженно-деформированного состояния стержней и трехмерных тел, были найдены корректирующие коэффициенты сдвига. К тому же, в случае на растяжение сделан вывод, что чем дальше по сечению от заделки находится координата сечения, тем меньше разница между известной и полученной формулами для модуля жесткости на растяжение. Также удалось систематизировать данные и сделать вывод о влиянии формы сечения на коэффициент сдвига при поперечном сдвиге. А именно: при увеличении длин сторон сечения и уменьшения его ширины, коэффициент сдвига будет значительно увеличиваться, стремясь к 1, коэффициент сдвига не зависит от положения сечения. Кроме того, полученные результаты были нанесены на график, после чего стало очевидно, что точки можно довольно точно аппроксимировать кривой. С помощью уравнения этой кривой можно получить коэффициент сдвига, используя 2 момента инерции.
Список литературы[править]
- Власов В. 3., Тонкостенные упругие стержни, 2 изд., М., 1959.
- В. И. Водопьянов, А. Н. Савкин, О. В. Кондратьев. Курс сопротивления материалов с примера и задачами. Учебное пособие, 2012.
- Тимошенко С. П, Устойчивость стержней, пластин и оболочек (избранные работы С. П. Тимошенко). — М.: Наука, 1971.
- П. А. Жилин. Прикладная механика. Теория тонких упругих стержней. Издательство Политехнического университета, 2007
- В. К. Манжосов. Сопротивление материалов. Определение внутренних силовых факторов. - Учебное пособие. Ульяновск, УлГТУ.
- Феодосьев В. И. Сопротивление материалов. — М.: изд-во МГТУ им. Н. Э.
Баумана, 1999
- Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. В 10-ти т. Т. VII. Теория
упругости: Учеб. пособие. — 4-е изд., испр. и доп. — М.; Наука. Гл. ред. физ.-мат. лит., 1987. — 248 с.
- Erasmo Carrera, Gaetano Giunta, Marco Petrolo. Beam Structures: Classical and Advanced Theories.
- O. A. Bauchau, J. I. Craig. Euler-Bernoulli beam theory. Springer Netherlands, 2009.