Моделирование материала с эффектом памяти формы

Выпускная квалификационная работа

Выполнил: студент группы 43604/1 П.Ю. Булдаков

Руководитель: кандидат физ.-мат. наук, доцент каф. "Теоретическая механика" О.С. Лобода

Введение

В последнее время в науке, технике и медицине все большее применение находят многофункциональные материалы с заданными свойствами – материалы, которые под действием внешних факторов и условий эксплуатации (температуры, механической нагрузки и т.д.) могут управляемо изменять свои свойства. Безусловно, к таким материалам относятся сплавы с уникальными и совсем недавно неизвестными физико-механическими свойствами – эффектом памяти формы (ЭПФ), явление возврата к первоначальной форме при нагреве после пластической деформации. Это явление наблюдается у некоторых материалов после предварительной деформации в строго определенном для каждого сплава интервале температур. Связан эффект с особым видом пластической деформации – мартенситными превращениями.

Цель и задачи работы

Моделирование сплава с ЭПФ рассмотрено в контексте проекта, в котором изучались функционально-механические свойства сплава, как материла для устройства, устраняющего пролапс митрального клапана. В качестве материала был выбран сплав никелида титана NiTi марки ТН-1. Цель данной работы заключалась в моделировании поведения проволоки из данного сплава при одноосном растяжении. В связи с поставленной целью в работе решаются следующие задачи:

• Экспериментально исследовать функционально – механические свойства никелида титана Ti - 50.84 ат. %Ni диаметром 0.5 мм и Ti - 50.81 ат. %Ni диаметром 0.7 мм марки ТН-1 фирмы МАТЭК-СПФ при разных температурах окружающей среды после различных режимов термообработки;

• По данным эксперимента провести расчеты одноосного растяжения двумя методами: микромеханическим подходом Мовчана для сплавов с ЭПФ и методом конечных элементов в программной системе ANSYS Mechanical;

• Сравнить результаты расчетов с экспериментальными данными;

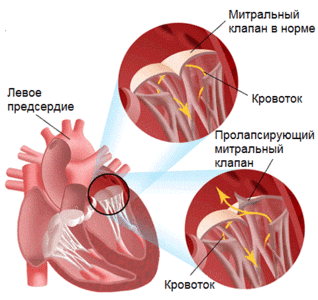
Пролапс митрального клапана и его коррекция

Пролапс митрального клапана (ПМК) (рис. 1) – это провисание створок митрального клапана в полость левого предсердия во время систолы, что при-водит к обратному току крови через клапан и может вызвать такие осложнения, как эндокардит, разрыв хорд и тромбоэмболия. Распространенность ПМК среди населения по одним данным оценена в 2–3% [1], по другим в 5–10% (у взрослой популяции). В большинстве случаев хирургическое вмешательство не требуется, но при высокой степени провисания створки необходима дорогостоящая операция с большим риском для жизни, так как для ее проведения требуется остановка сердца.

• 

  Рисунок 1. Пролапс митрального клапана

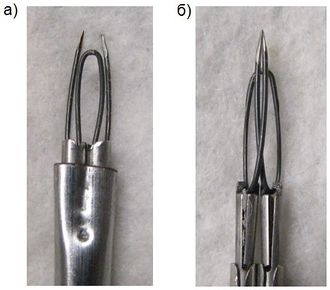
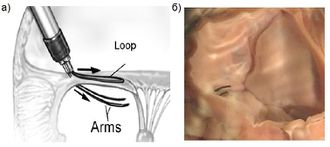
LPC (Leaflet Plication Clip) [2] был разработан в Бостонской детской больнице и представляет из себя специально изогнутую проволоку из сплава никелид-титана (NiTi). Установка LPC (рис.3) на пролапсирующий митральный клапан является альтернативой хирургическому методу лечения и может быть выполнена без остановки сердца. LPC изначально задают форму как показано на рисунке 2 (б). Во время операции его «взводят» (рис. 2, 3 а) при помощи специального инструмента и крепят на пролапсирующую створку митрального клапана, за счет того, что он выполнен из материала с ЭПФ, LPC «схлопывается» в свою исходную форму, тем самым сжимая провисающую часть створки и прекращая митральную регургитацию (ток крови в обратную сторону) (рис. 3 б). В данном случае используется свойство cверхупругости, которое присуще материалам с ЭПФ.

• 

  Рисунок 2. LPC в «взведенном» состоянии (а) и в исходной форме (б)

• 

  Рисунок 3. LPC в «взведенном» состоянии (а) и в исходной форме (б)

Эффект памяти формы

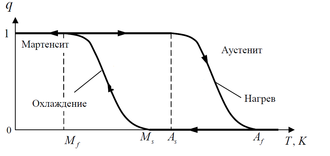
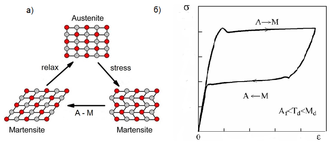
Эффект заключается в способности ненагруженного материала под воз-действием внешнего напряжения и изменения температуры накапливать де-формацию до 10–15%, обратимую при нагреве за счет фазовых превращений (мартенситных). Кинетика мартенситных превращений имеет ярко выраженный гистерезис (рис. 4). Если материал охлаждать из аустенитного состояния, то вначале каких-либо фазовых преобразований не происходит. Однако начиная с некоторой характеристической температуры, которую принято обозначать Ms , появляются первые кристаллы мартенсита, следовательно, увеличивается и доля мартенситной фазы в объеме материала. По мере дальнейшего охлаждения их размеры и количество увеличиваются, пока кристаллы не заполнят при температуре Mf весь объем. Такое превращение называется прямым и при наличии внешней нагрузки сопровождается появлением большой деформации (эффект пластичности превращения). При последующем нагреве, после преодоления температуры As мартенсит начинает переходить в аустенит. При этом накопленная деформация медленно исчезает до тех пор, пока температура не станет выше Af и не произойдет восстановление формы. Температуры мартенситных превращений сильно зависят от химического состава сплавов, их термической и механической обработки.

• 

  Рисунок 4. Схема зависимости объемной доли мартенсита q от температуры T

Также было отмечено, что механические напряжения инициируют перестройку кристаллической решетки, то есть действуют аналогично температурному фактору. Допустим, что к кристаллу, который находится в аустенитном состоянии при температуре деформирования Тd, начали прикладывать внешнее напряжение. Тогда температура Ms (в соответствии с известным термодинамическим уравнением Клаузиуса-Клапейрона) будет повышаться подобно тому, как растет температура кипения воды под давлением. При каком-то значении напряжения она достигнет значения Тd или превзойдет данный уровень. Это будет означать, что начнется реакция аустенит → мартенсит, которая приведет к образованию мартенсита, наведенного механическими напряжениями. Иными словами, кристалл испытает деформацию по каналу мартенситной неупругости. Если теперь удалить нагрузку, то характеристические температуры (Ms, Mf, Аs, Af) вернутся к первоначальному значению. И тут возможны следующие нетривиальные последствия: когда Тd > Af, возникший мартенсит станет термодинамически абсолютно неустойчивым. Значит, во время снятия нагрузки он с неизбежно превратится в аустенит, а приобретенная деформация полностью вернет-ся – это свойство называется сверхупругостью (рис. 5).

• 

  Рисунок 5. Схема (а) и диаграмма (б), иллюстрирующие эффект сверхупругости в никелиде титана при его деформации в состоянии устойчивого аустенита

Модель Мовчана

Микромеханический подход Мовчана заключается в рассмотрении зарождения и развития кристаллов мартенсита, которые дают определенный вклад в скорость изменения фазовой деформации в сплаве с эффектом памяти формы. Предполагается, что скорость роста кристаллов мартенсита пропорциональна накопленной фазовой деформации и уровню напряжений.Общая схема подхода изложена в [3]. Система определяющих соотношений формулируется следующим образом:

[math] ε = ε^e + ε^p [/math],

где [math] ε^e, ε^p [/math]– тензоры упругой и фазовой деформации. Для упругой деформации справедливы следующие уравнения:

[math] ε'^e = (σ')/2G [/math],

[math] ε^e= σ/K [/math],

где G, K – модули сдвига и объемного сжатия, соответственно. Штрих обозначает девиатор соответствующего тензора. Для фазовой деформации используются уравнения:

[math] dε^p =( c_0 σ' + a_0 ε^p)dq[/math] при dq > 0,

[math] dε^e = ((a_0 ε^0)/((exp⁡(a_0 )-1)) + a_0 ε^p )dq [/math] при dq < 0,

[math]q_1 = cos[π/2 ((T-k√(σ σ )- M_f)/(M_s- M_f )) ] [/math] при dq > 0,

[math]q_2 = cos[π/2 ((T-k√(σ σ )- A_s)/(A_f- A_s )) ] [/math] при dq < 0,

[math]1/(E(q)) = q/E_1 + (1-q)/E_2 [/math].

Здесь Е1, Е2 – значения модуля Юнга для мартенситного и аустенитного со-стояния; a0, k, c0 – коэффициенты материала, которые можно найти из опыта на прямое превращение. Уравнения (3) и (5) соответствуют прямому превраще-нию, а (4) и (6) – обратному. MS, Мf, АS, Аf – температуры начала и завершения прямого и обратного мартенситного превращения.

Конечно-элементная модель

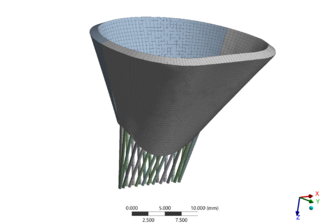
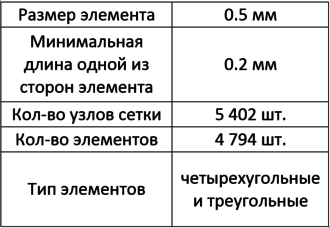
По описанной выше геометрической модели была построена конечно-элементная модель митрального клапана (рисунок 6).

• 

  Рисунок 6.Конечно-элементная модель митрального клапана.

• 

  Рисунок 7.Параметры конечно-элементной модели.

Начальные и граничные силовые условия

Начальные и граничные условия задачи будем ставить исходя из реальных условий работы сердца. В начальный момент расчета клапан находится в ненапряженном состоянии, что соответствует переходу от этапа наполнения к этапу систолы предсердий.

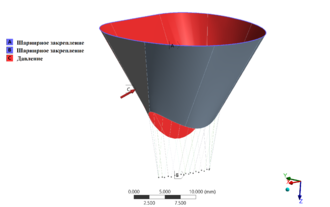
Граничные силовые условия схематично отображены на рис.8. Для митрального кольца ограничены перемещения по трем трансляционным степеням свободы (A). Также ограничены перемещения (B) нижней части хорд, которой они крепятся к стенкам левого желудочка. По нормали приложено поверхностное давление (C), обеспечивающее смыкание створок.

• 

  Рисунок 8.Граничные силовые условия.

Результаты

Ниже приведены анимации, иллюстрирующие полный цикл работы митрального клапана

• 
• 

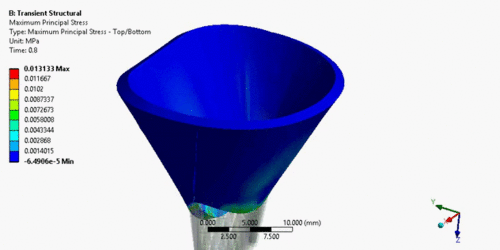
Наибольшие напряжения наблюдаются во время перехода от фазы напряжения к фазе изгнания на 0.302 сек расчета, в этот момент на створки действует результирующее давление 16 кПа, именно этот момент считается полным закрытием клапана. В момент полного закрытия возникает колебание створок, которое вызвано тем, что скорость потока крови резко падает и не может преодолеть закрытый клапан. И кровь, и створки клапана обладают импульсом, который сначала преобразуется в энергию деформации, затем возвращается в виде ускорения потока, а заем снова преобразуется в энергию деформации и так до тех пор, пока клапан не достигнет устойчивого равновесия.

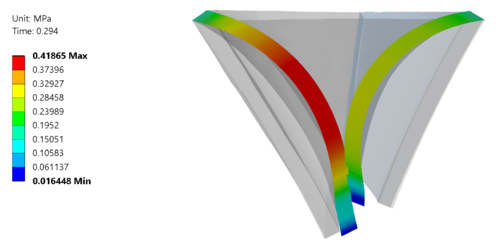
Смыкание клапана подтверждено проверкой статуса контактных элементов (рис. 9) в момент пиковых напряжений. Также на рис. 10 изображено серединное сечение явно описывающее плотное смыкание клапана.

• 

  Рисунок 9.Серединное сечение клапана в момент максимального смыкания клапана.

• 

  Рисунок 10.Контактное давление в момент максимального смыкания клапана.

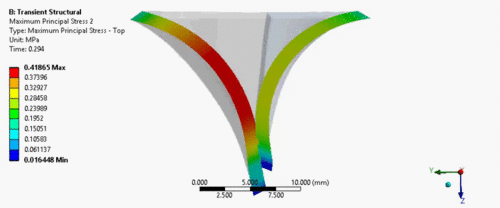
Напряжения на передней створке всегда больше чем напряжения, возникающие на задней. В целом, значения напряжений варьируются в пределах от 13 кПа в период напыления желудочка до 637 кПа в период полного смыкания клапана. Этот результат хорошо согласуется с данными, полученными в статьях [7][8][9], посвященных исследованиям митрального клапана.

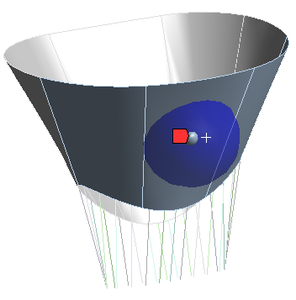
Также, в рамках данной задачи был проведен анализ влияния устройства “Клип” на створки митрального клапана при его нормальной работе. “Клип” моделировался в виде точечной массы с заданной областью влияния. Устройство было установлено на задней створке в центре (рис. 11).

• 

  Рисунок 11. Расположение точечной массы на поверхности задней створки: малая сфера – область установки “Клипа”.

Масса устройства рассчитывается по формуле:

[math] m= 4 l_с ρ π r^2 [/math]

где l_с – максимальное расстояние от митрального кольца до свободного края створки, ρ = 6.4 г/см3 – плотность нитинола, r – радиус нитиноловой проволоки.

Таким образом, масса скрепки может варьироваться от 0.1 до 0.4 грамм. В работе рассмотрены 3 случая: а) масса скрепки - 0.1 грамм, что соответствует проволоке с радиусом 0.5 мм; б) масса скрепки - 0.23 грамма, радиус - 0.75 мм; в) масса скрепки - 0.4 грамма, радиус – 1 мм. Для данных трех типов скрепки был проведены расчет и сравнение полученных результатов со случаем, когда на створке нет установленного “Клипа”.

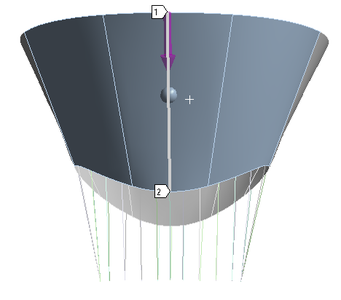
Анализ перемещений вдоль линии, указанной на рис.12а, показал, что максимальное расхождение результатов составляет 0.18% и обнаружено оно при сравнении случая без “Клипа” и случая в) Мс = 0.4 г. Это говорит о том, что установка скрепки не оказывает значительного влияния на перемещения створки митрального клапана при его нормальном функционировании.

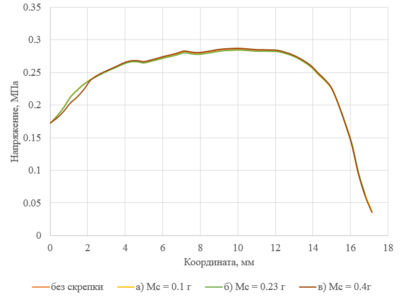
На графике 12б приведены значения напряжений на линии установки “Клипа” (рис. 12а) для трех случаев в сравнении с решением, когда на створке нет “Клипа”.

• 

  Рисунок 12а.Линия вывода напряжений вдоль поверхности створки.

• 

  Рисунок 12б.График зависимости напряжения от координаты на рассматриваемой линии для трех видов “Клипа” и створки без него.

Для случаев, а) и б) не наблюдается большого расхождения с данными для решения без учета скрепки. Однако при увеличении массы наблюдается расхождение результатов в верхней области клапана. Максимальное значение расхождения результатов – 5.11% обнаружено в случае в) когда масса скрепки равна 0.4 г. В статье Anwarul Hasan “Biomechanical properties of native and tissue engineered heart valve constructs” [12] приведено значение динамического предела прочности 0.9 МПа для материала створок митрального клапана. Таким образом, можно сделать вывод, что установка “Клипа” не повлечет за собой появление дополнительных растягивающих напряжений на створках клапана, способных привести к появлению необратимой деформации створок митрального клапана.

Обработка данных c компьютерного томографа

Также, одной из задач, как было заявлено выше, является создание 3D модели используя данные, полученных с компьютерного томографа. Данный процесс можно разделить на два этапа: а) Перевод облака точек из формата DICOM в формат STL; б) Создание твердотельной геометрии из STL.

а) Перевод облака точек из формата DICOM в формат STL.

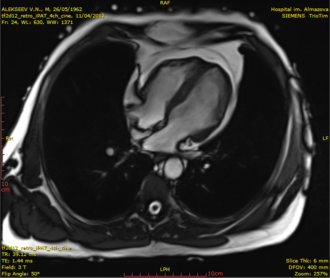
Принцип действия компьютерного томографа заключается в одновременном выполнении трех действий: непрерывного вращения вокруг тела пациента рентгеновской трубки, испускающей рентгеновское излучение; регистрации этого излучения, проходящего сквозь тело человека, специальными детекторами-матрицами; непрерывного движения кушетки вдоль продольной оси вместе с лежащим на ней человеком. После прохождения через тело пациента лучи фиксируются матрицами-детекторами, преобразуются в электрические сигналы, и передаются на компьютер. Компьютер томографа обрабатывает эту информацию, поступившую с детекторов излучения, и в результате создается двухмерное изображение поперечного сечения тела на разных уровнях, так называемые "срезы"(рисунок 13).

• 

  Рисунок 13.Снимок компьютерного томографа.

Если сравнить разрешение магнитно-резонансной томографии, компьютерной томографии и компьютерной томографии, проведенной на малогабаритном компьютерном томографе (рис. 14), можно сделать вывод, что для получения анатомически точной модели митрального клапана необходим именно малогабаритный компьютерный томограф, т.к. только он позволяет обнаружить хорды митрального клапана.

• 

  Рисунок 14.Сравнение разрешения для МРТ, КТ и мКТ.

Снимки компьютерного томографа (рисунок 13) являются визуализацией DICOM данных полученных при проведении обследования. DICOM (англ. Digital Imaging and Communications in Medicine) — отраслевой стандарт создания, хранения, передачи и визуализации медицинских изображений и документов обследованных пациентов.

• 

  Рисунок 15. STL модель части позвоночника.

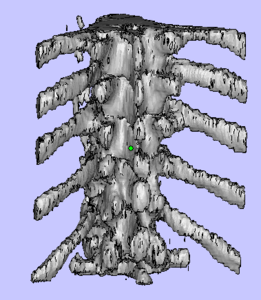
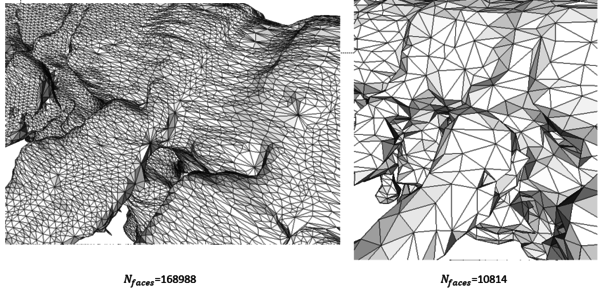
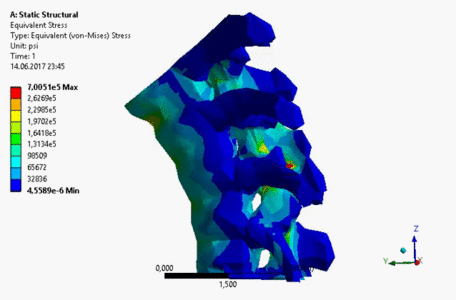
С помощью программного пакета 3D Slicer, путем обработки DICOM файлов, построена STL модель части позвоночника человека (рисунок 15). Т.к. полученная модель имеет много лишних поверхностей и неровностей, вызванных шумовыми эффектами при проведении томографии, с помощью программы MeshLab модель была отфильтрована (рисунок 16).

• 

  Рисунок 16. Сравнение кол-ва поверхностей до фильтрации и после.

б) Создание твердотельной геометрии из STL.

Формат STL широко используется для хранения трехмерных моделей объектов для использования в технологиях быстрого прототипирования. Информация об объекте хранится как список треугольных граней, которые описывают его поверхность, и их нормалей. Но для использования при проведении расчетов в инженерных пакетах программ требуется построение твердотельного геометрии CAD модели. Таким образом, с помощью программы ANSYS SpaceClaim вышеуказанная STL модель была конвертирована в CAD модель, представляющая собой твердотельную геометрию.

• 

Ограничения и допущения

При выполнении вышеизложенного анализа, было принято несколько допущений. Во-первых, модель материала как хорд, так и створок должна обладать свойствами анизотропной гиперупругости. В случае с хордами, смоделировать гиперупругость не позволяет само определение элементов BEAM188 для моделирования балочных элементов. В целом, для построения качественной анизотропной гиперупругой модели материала требуется проведение ряда экспериментов для определения констант входящих в выражение для описание такой модели. В данной работе материал створок и хорд был смоделирован как линейный гиперупругий в первом приближении.

Во-вторых, для детального исследования поведения митрального клапана при работе сердца и определения положения устройства “Клип” на створке клапана требуется анатомически точная модель клапана, полученная из данных с компьютерного томографа высокого разрешения. В силу недоступности данного оборудования, геометрическая модель клапана была построена по анатомическим атласам с размерами, проверенными в статьях, направленных на изучение анатомии митрального клапана.

Выводы

В рамках данной задачи выполнено численное моделирование работы митрального клапана в сердце человека. По анатомическим атласам построена балочно-оболочечная геометрическая модель с учетом неоднородности распределения толщины клапана по поверхности створок. С помощью программной системы конечно-элементного анализа ANSYS Mechanical проведено моделирование для полного цикла работы митрального клапана. При численном решении данной задачи был выбран тип анализа Transient structural (нестационарный структурный анализ), позволяющий определять изменяющиеся во времени перемещения, деформации, напряжения и внутренние усилия в теле под воздействием нестационарных нагрузок. При моделировании материала створок митрального клапана была выбрана линейная изотропная модель.

Полученные результаты для напряжений, возникающих на створках хорошо согласуются с данными, полученными в статьях [7][8][9], посвященных моделированию работы митрального клапана. Так же, в рамках численного моделирования было доказано, что клапан плотно смыкается во время перехода от фазы напряжения к фазе изгнания на 0.302 сек расчета, это совпадает данными для цикла работы клапана.

Помимо моделирование нормально функционирующего клапана, проведено моделирование работы клапана с устройством “Клип” на задней створке. Анализ полученных результатов позволят заявить, что установка “Клипа” не повлечет за собой появление дополнительных растягивающих напряжений, способных привести к необратимым деформациям створок митрального клапана.

Так же стоит отметить, что в рамках данной работы, на примере части позвоночника человека, реализован и отработан способ обработки данных с компьютерного томографа в твердотельную модель, которую в дальнейшем можно использовать при расчетах в программных системах конечно-элементного анализа. Данный способ, позволит в будущем построить анатомически точную модель митрального клапана по данным обследования компьютерным томографом.

В дальнейшем в рамках реализации данной задачи планируется использование несжимаемого, гиперупругого трансверсально-изотропного материала и построение геометрической модели клапана по данным с компьютерного томографа для более точного изучения поведения створок нормально функционирующего митрального клапана.

Список литературы

1. World Health Organization. The world health report 2016. (http://www.who.int)

2. American Heart Association. Heart disease and stroke statistics Update 2005. (http://www.americanheart.org)

3. Gillinov A.M, Wierup P.N., Blackstone E.H., Bishay E.S., Cosgrove D.M., White J., Lytel B.W., and McCarthy P.M. Is repair preferable to replacement for ischemic mitral regurgitation? The Journal of Thoracic and Cardiovascular Surgery 2001; 122, 1125-1141

4. Sacks M.S., He Z., Baijens L., Wanant S., Shah P., Sugimoto H., and Yoganathan A.P. Surface Strains in the Anterior Leaflet of the Functioning Mitral Valve. Annals of Biomedical Engineering 2002; 30, 1281-1290

5. https://ru.wikipedia.org/wiki/Сердечный_цикл

6. Д . С . Котович, И.Н. Стакан Анатомия митрального клапанного аппарата в норме и при дилатационной кардиомиопатии.

7. Kunzelman K.S., Einstein D.R. and Cochran R.P. Fluid-structure interaction models of mitral valve: function in normal and pathological states.

8. Stevanella, M., F. Maffessanti, C. A. Conti, E. Votta, A. Arnoldi, M. Lombardi, O. Parodi, E. G. Caiani, and A. Redaelli. Mitral valve patient-specific finite element modeling from cardiac MRI: application to an annuloplasty procedure.

9. Qian W. and Wei S. Finite Element Modeling of Mitral Valve Dynamic Deformation Using Patient-Specific Multi-Slices Computed Tomography Scans.

10. Humphrey, J. D., Strumpf, R. K., and Yin, F. C. P., 1990a, "Determination of a constitutive relation for passive myocardium: I. A new functional form, ASME JOURNAL OF BIOMECHANICAL ENGINEERING, Vol. 112, pp. 333-339.

11. Mohd Azrul Hisham Mohd Adib, Kahar Osman, Nur Hazreen Mohd Hasni, Oteh Maskon, Faradila Naim, Zulkifli Ahmad, Idris Sahat1and Ammar Nik Mu’tasim. Computational Simulation of Heart Valve Leaflet under Systole Condition using Fluid Structure Interaction Model.